考虑低电压穿越的风电场双机聚合模型
2016-02-16高峰黄鸣宇乔颖阮佳阳
高峰,黄鸣宇,乔颖,阮佳阳
(1. 国网宁夏电力公司电力科学研究院,银川市 750002;2.电力系统国家重点实验室(清华大学电机系),北京市 100084)
考虑低电压穿越的风电场双机聚合模型
高峰1,黄鸣宇1,乔颖2,阮佳阳2
(1. 国网宁夏电力公司电力科学研究院,银川市 750002;2.电力系统国家重点实验室(清华大学电机系),北京市 100084)
场内风速分布不均、集电线路分布不匀等因素造成各发电机间继电保护状态和外特性的差异,使得常规单机聚合模型难以准确反映真实风电场的故障穿越行为。为此,基于逆向建模方法与宏观特征参数,提出了对双馈异步机组(doubly-fed induction generator,DFIG)风电场具有更强适应的双机聚合模型。首先,分析了过流短接保护对风电场外特性指标的影响。其次,考虑到DFIG的功率源特性,低电压穿越中对其转子侧Crowbar的描述决定了是否能精确模拟风电场的功率调制响应,而短路电流水平又决定了Crowbar是否动作,是引起发电机间调性不同的最主要因素。基于该不同调性对故障过程中的DFIG进行分类,在双机等值模型的基础上实现了对风电场内分布行为的描述,并可根据具体风电场参数和风资源特性主动调节宏观参数组,从而平滑设定影响外特性的场内分布因素水平。最后,为提高该模型的实用性,还提出了一套参数辨识策略,依据故障深度提取出能体现风电场于该次扰动中最大的可能性响应的宏观参数组。多机系统仿真验证了单机等值存在的问题以及双机等值模型的性能。所提方法可考虑风电场自身的风资源特性,同时有效提高对风电场功率响应、相邻同步机功角稳定和负荷电压稳定行为的模拟精度。
双机聚合模型;暂态稳定;Crowbar效应;低电压穿越;风速分布
0 引 言
电力电子接口发电机属于新型异步电源,转子旋转频率可与同步电网保持异步,其动态行为和稳定机理都明显区别于传统的同步机,与同步机间的互动也十分复杂。以风力发电机为例,对于风火打捆等运行方式,大扰动下邻近的同步机出现功角摇摆并引发异步电源并网点的电压振荡,进而与其低电压穿越、功率恢复等事件耦合,形成一系列特殊的动态稳定行为[1-3]。
目前,在进行安全稳定计算时,一般将含有大量小容量、同型号风力发电机的风电场时以聚合等值方式进行工程化建模,但如何描述“聚合”对于稳定性计算的影响尚无定论。由不同类型异步电源组成的风电场,其建模适应性问题的研究难度也不尽相同。常见的风力发电机包括鼠笼异步机组(squirrel-cage induction generator,SCIG)、双馈异步机组(doubly-fed induction generator,DFIG)和永磁直驱机组(permanent-magnet synchronous generator,PMSG)。其中,SCIG没有励磁控制与直流环节的电压脉宽调制,建模方法成熟;PMSG通过全功率变流器与电网耦合,故障期间始终保持功率可控,功率调制行为也相对容易描述;DFIG同时通过发电机回路和变流器与电网耦合,且有特殊的复杂低电压穿越动态,因而暂态稳定计算中大规模DFIG风电场的建模一直没有形成较为统一的体系。
目前,工程中多采用单台机等值表征DFIG风电场[4-6],即把风电场替换成1台风力涡轮和1台等值发电机。也有研究将各台风力发电机的轴系模型保留,而电气部分等值成1台发电机,计算等值机的等效转速和电磁转矩指令作为其动态方程的输入[7-8]。然而,大型风电场受地形、地貌以及尾流效应的影响,风场内风速分布极不均匀,使用单机等值表征整个风电场易产生较大误差[9-10]。问题的根源在于单机等值无法描述处于不同地理位置、不同工况发电机间的不同调,因而一些研究提出按风速分布进行机群分类的多机等值思路[11-13],但是风电场中各台风力发电机的海量风速、功率信息并不容易精确获取[14],导致机群分类在实际运行中可操作性差。另外,分群数随风电场内风速差异的增大而增加,在重复、频繁进行的大规模系统级计算中的实用性有限。
单机等值法不能描述因风速分布造成的风力发电机间的不同调,而多机等值法又偏离工程应用要求。为此,本文提出一种综合考虑操作复杂度和仿真精度要求的改进聚合等值模型。提出的描述风电场内部状态的宏观特征参数可平滑设定分布性水平,从而尽量精确地模拟真实风电场的响应。
1 风电场聚合模型的适应性分析
1.1 风电场等值模型分类
“单台机(聚合)等值”采用1台容量放大的等值发电机代替所有小容量的发电单元,如图1 (a)所示。等值机容量为投运发电机容量之和,参数标幺值、控制参数与单台机相同,模型形式也完全相同。取等值机运行点为所有被等效发电机的平均运行点,并在风电场出口添加1个等值阻抗来计及场内集电线路损耗。等值机中也含有轴系模型,因此单台机等值性能的关键是获得1个输入等值风速,目前研究主要集中在等值风速以及等值阻抗的获取方法上[15-16],可根据损耗相同原则获取等值阻抗。
单台机等值方法简单,可以通过改变等值风速来调整断面有功功率。其缺点也很明显:可调变量少,难以反映场内各台风力发电机风速、集电线路差异带来的分布性,无法表现同一出力状态下分布因素导致的响应差别。更重要的是,同一个出力水平下等值机的Crowbar只能处于完全动作或不动作的状态,没有中间状态。而实际运行经验表明,多数电压跌落过程中只有部分发电机的Crowbar会动作而短暂地进入不可控态[17],另一部分发电机的Crowbar则并没有动作,仍然保持双馈可控状态。
改进思路是增加等值机台数。如图1(b)所示,采用多台机等值能够在一定程度上反映风速分布的影响。当前的多台机等值仍需事先输入场内各台发电机的风速(或通过一定的算法模拟产生一组风速),将运行点相似的机组聚类为1台等值机。然而,实际应用中多数计算场合无法精确获得场内所有发电机的风速。特别是在功率由风功率预测得到的场景下,只有整场的出力点值是可知的。
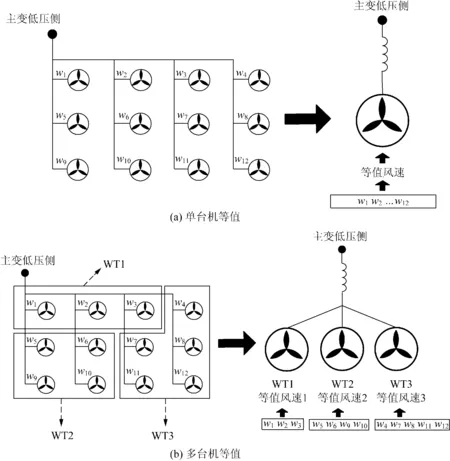
图1 风电场“单机等值”与“多机等值”建模Fig.1 Single-machine and multi-machine equivalent modeling of wind farms
电力系统暂态仿真分析主要关注风电场在低电压穿越期间的功率调制外部特性,如剩余有功和增发无功与电压跌落程度的映射关系。据此,本文认为,适用性更强的风电场聚合模型应满足要求:
(1)为反映分布性的特征,聚合模型的结构必须采用至少2台等值机的形式;(2)同调机群的划分与发电机动态数学模型的具体物理量间可以建立简单、确定的映射关系,从而保证聚合的易操作;(3)划分指标可以反应故障过程中Crowbar可能发生动作的机组比例,以及可能失去的(可控部分)功率输出;(4)在已知整场出力的边界条件下反映风电场所可能产生的最大可能响应。
1.2 单台DFIG的Crowbar动作策略及影响
实际投运风电场的Crowbar动作策略分为2类,这2种策略的相同点都是在电压跌落瞬间投入Crowbar,转子通过外接电阻短接并闭锁变流器。不同之处在于Crowbar的切出策略,一种是在转子电流幅值衰减至切出阈值时立即切出Crowbar并启动变流器,而另一种则在Crowbar切入后进行一个固定的延时保持,继而在短路电流充分衰减后切出Crowbar。前一种策略的优点是Crowbar作用时间极短,此策略对DFIG可控性的影响在机电暂态时间尺度内可以忽略不计[15],发电机近似于一直处于双馈状态,但可能出现故障期间Crowbar多次投切而使得设备电气应力增大;后一种策略可以确保Crowbar只投切1次,但延时保持期间DFIG按SCIG方式运行,吸收相当的无功,低风速下甚至转为电动机状态,不能对电网提供功率支撑。显然,后一种策略造成的发电机间不同调效应更显著,本文主要考虑该策略。
为使转子过电流尽快衰减,通常采用较高的Crowbar电阻值Rc。这样设置的另外一个好处是保护动作的DFIG在故障期间吸收的无功较普通的SCIG大为降低。图2是Crowbar电阻为不同值时的异步电机功率外特性。
可见当Rc增至5倍转子电阻值以上时,发电机有功功率与转差率在可运行的转速范围内已呈近似单调关系。图2(b)中,Crowbar保护动作的DFIG所吸收无功功率随Rc值的增大迅速降低,且同一条曲线的峰值峰谷差距减小,在转差率小于0和大于0的

图2 Crowbar动作期间发电机的输出功率-转差特性Fig.2 Power-slip curves of generator when Crowbar activating
这2个区间内分别变得近似线性。这样,故障前不同运行点的DFIG进入SCIG状态后输出的功率具有强同调性,满足叠加条件。可以推断,将所有Crowbar动作的发电机替换成1台等值SCIG在工程上是合理的。
1.3 分布性特征对风电场外特性的影响
风功率预测只能得到电站的整场出力,因此风速的分布性就决定了风电场对电力系统暂态稳定计算贡献的涨落。具体表现为,风电场同等出力水平的前提下,2次暂态稳定计算的结果出现差别。
低电压穿越过程中一种常见的情形是风电场中只有部分发电机的Crowbar保护动作。本文以图3中的最简原型系统说明风电场内“分布性因素”对电力系统分析的影响机理。假定2个机群内各自的发电机出力完全相同。整场功率保持一定时,2个机群的Crowbar可能都动作或都不动作,也可能只有1个机群动作,这取决于具体的出力分布、参数配置与故障深度。
首先,假定该风电场的总出力为0.515 pu。假设风速分布均匀,两机群各含10台机,出力水平分别为0.72和0.31pu,图4为风电场出口处发生电压跌落的仿真结果。图中两机群内DFIG的转子电流峰值均未达到阈值2.0 pu,因此Crowbar都没有动作。故障期间发电机输出功率一直保持可控,在故障发生瞬间有功指令迅速降为0,无功指令按低电压穿越指标发出。两机群具有很强的同调性,输出功率可以叠加。可以断定,虽然两机群的风速不同即故障前运行点不同,但由于两机群都一直保持在功率可控的双馈状态,常规单机等值模型的模拟效果可满足应用要求。图5验证了此时单台机等值的精度。

图3 风电场基本单元拓扑示意图Fig.3 Topology of elementary unit of wind farms
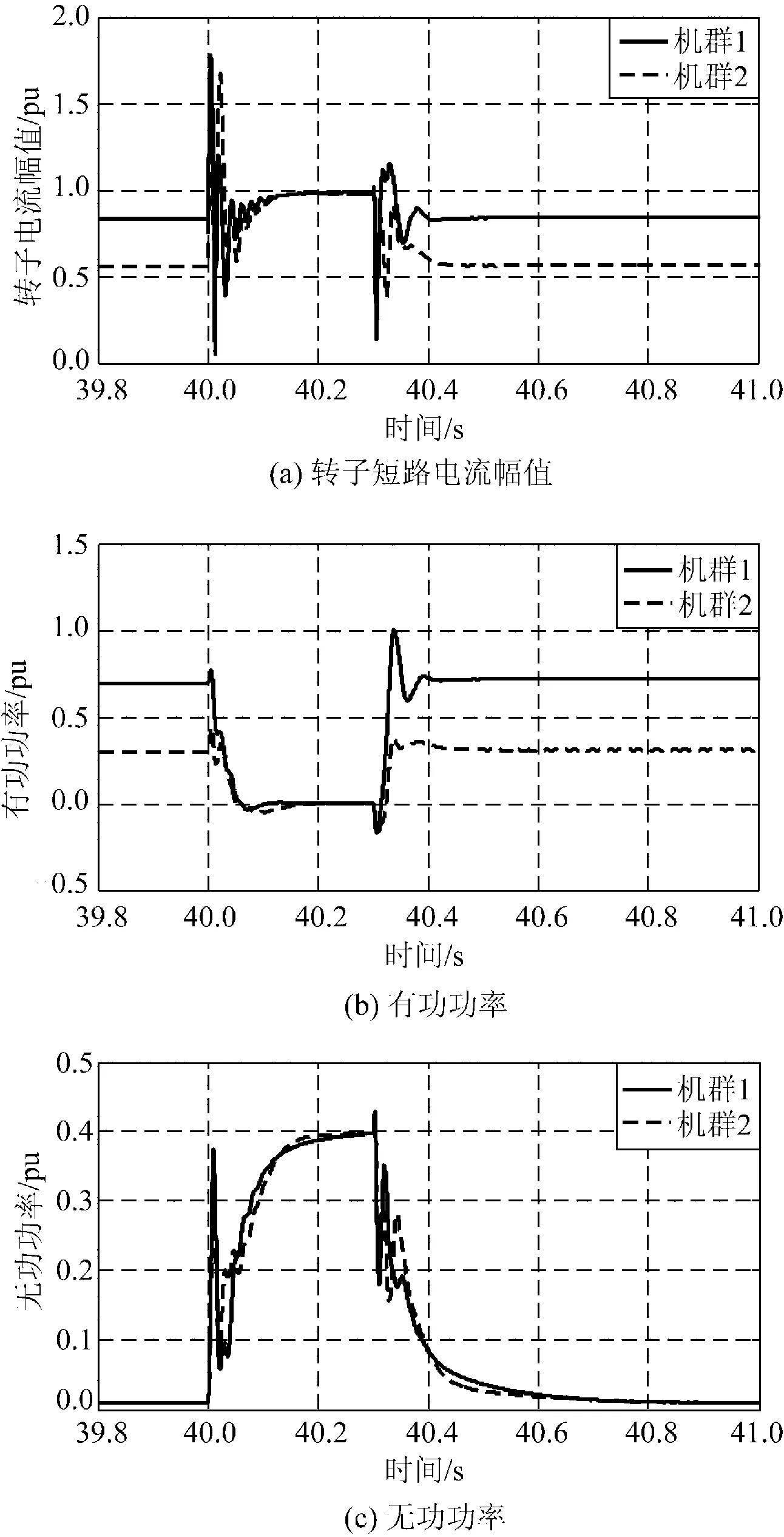
图4 双机群的Crowbar均未动作时各机群的响应曲线Fig.4 Power responses of wind farm when Crowbar of neither cluster is activated
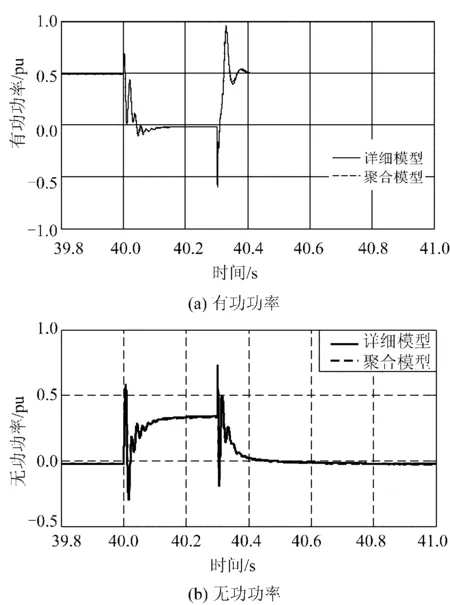
图5 双机群Crowbar均未动作时聚合模型的等值效果Fig.5 Equivalent results of aggregation model when Crowbar of neither cluster is activated
仍保持整场风功率为0.515 pu,设置机群1包括5台出力为1.0 pu的发电机,机群2包括15台出力为0.35 pu的发电机,仿真结果如图6。可见机群1短路电流幅值超限,在故障瞬间Crowbar保护动作,此状态保持0.10 s后才切回双馈状态。由于满发的机群1事先工作在超同步速,保护动作期间仍发出一定有功,吸收一定无功,但由于SCIG状态下吸收功率正比于电压平方,因而与电网交换的剩余功率极低。
聚合模型Crowbar没有动作,因而与详细模型产生了显著的误差,尤其是故障发生初期的无功功率,如图7。上述结果证实,在保持整个风电场的总出力恒定的前提下,2个不同风况中风电场的功率响应外特性出现了显著涨落。
2 风电场内部转子故障电流特点分析
决定场内DFIG不同调的因素(分布性因素)包括集电线路与风速分布。首先,研究前者引发的低电压穿越响应差异。对于图8中1组级联接入的发电机,假定风速相同,电气连接强度不同导致短路电流水平差别,并产生仅部分发电机Crowbar保护动作的可能。实际中还应考虑到:1根馈线不会太长,所连接的发电机通常不超过10台,且相邻发电机的间距不会超过1 km。因此集电线路分布引起的机端电压和短路电流峰值差别并不明显,该分布效应并不是主要因素。
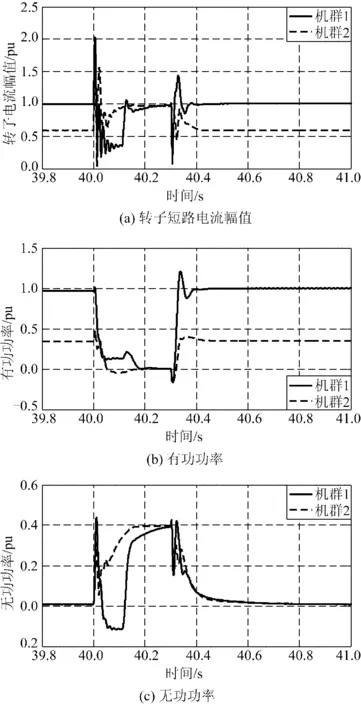
图6 仅机群1的Crowbar动作时各机群的响应Fig.6 Power response of wind farm when only Crowbar of cluster 1 is activated
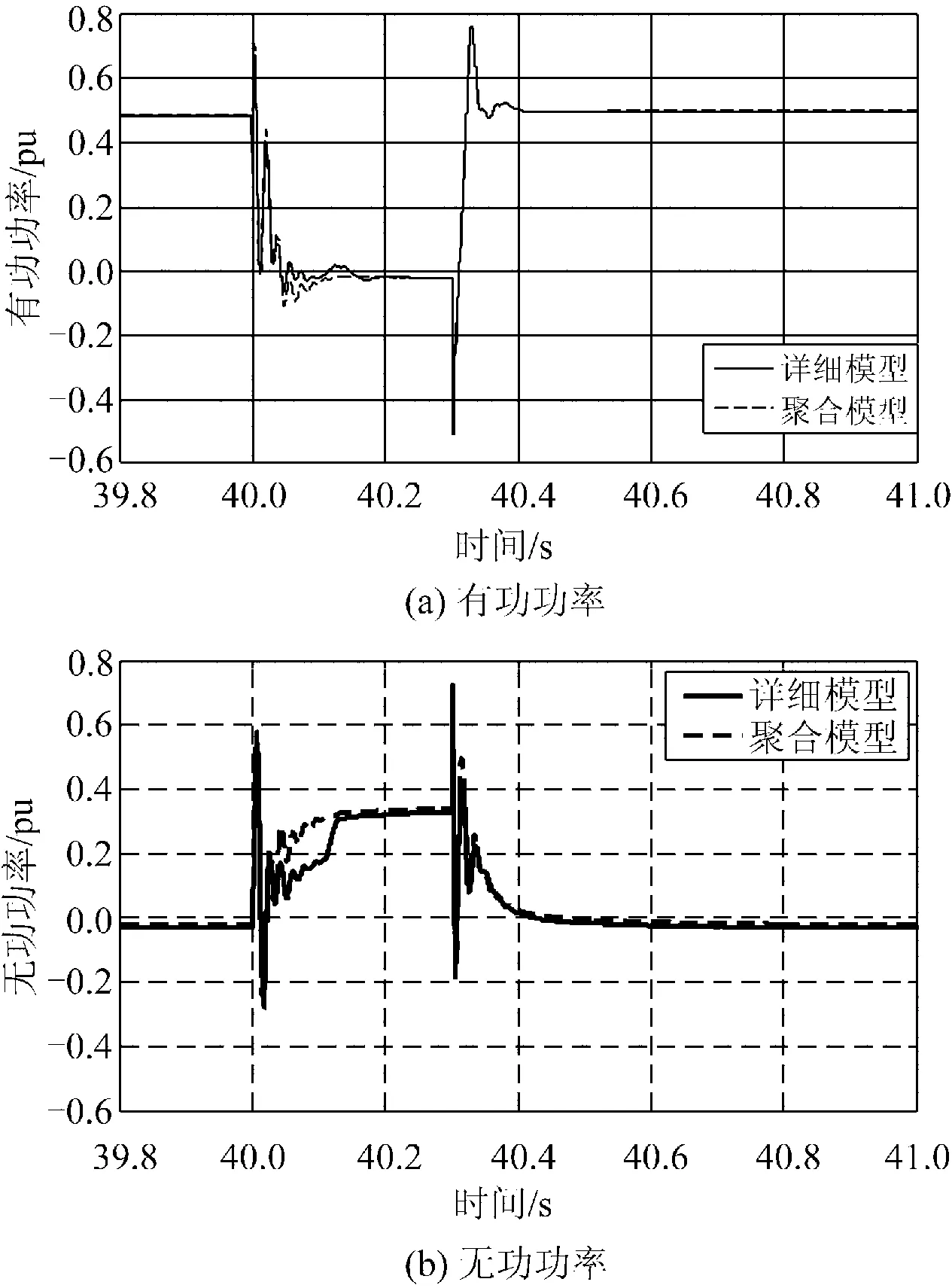
图7 仅机群1的Crowbar动作时聚合模型的等值效果Fig.7 Equivalent results of aggregation model when only Crowbar of cluster 1 is activated
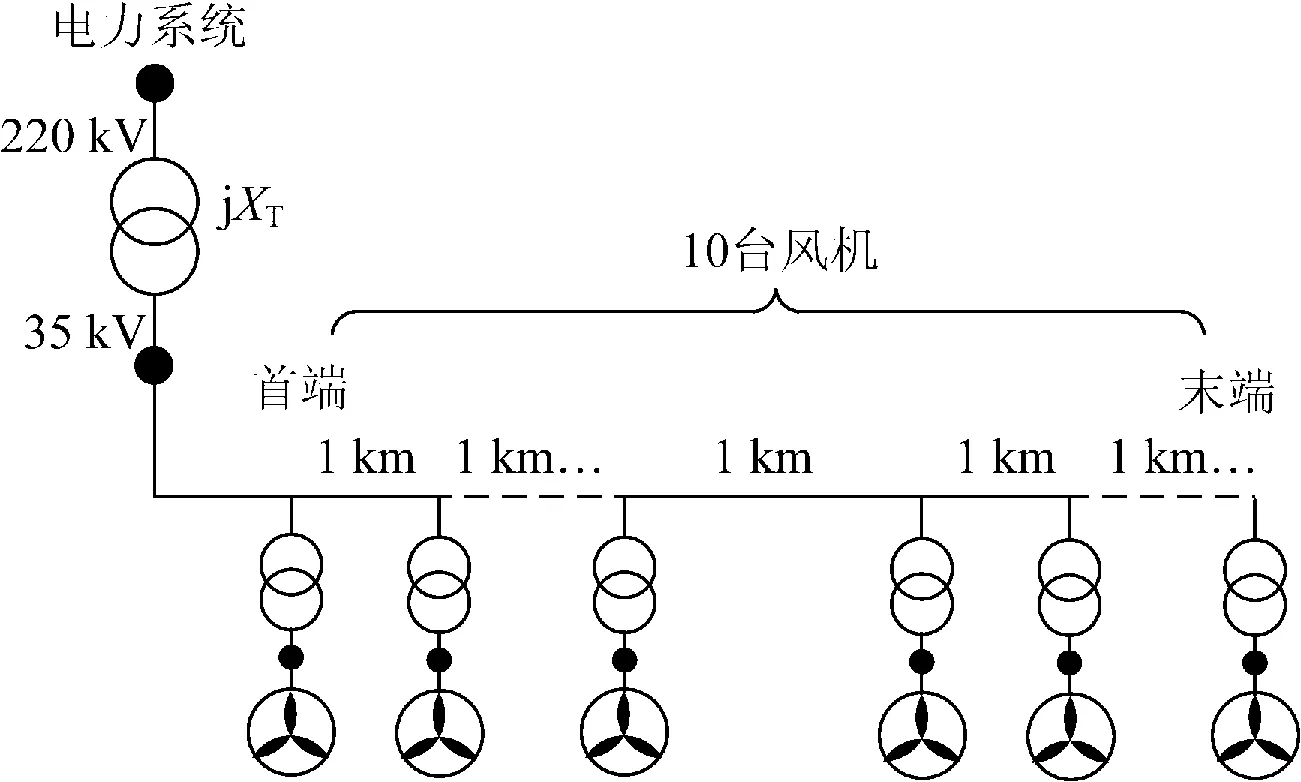
图8 风电场内部馈线结构示意图Fig.8 Internal feeder structure diagram of the wind farm
这一点在图9中能看出,集电线路导致的各台机机端残压差别微弱,馈线首端与末端发电机的短路电流峰值差别并不大,末端发电机的短路电流稍低,但峰值差别不超过0.10 pu。可以推测,建模中可以将风电场简化处理为所有发电机并联在同一点上集中送出。该简化将显著降低双机建模与参数辨识的复杂度。

图9 集电线路分布导致的转子短路电流峰值差异Fig.9 Differences in peak rotor current caused by collection-network distribution
相比之下,风速分布的影响要显著得多。图10(a)为不同出力水平下DFIG的短路电流幅值分布。可见,短路电流的第1个峰值随出力水平上升而大幅增加,而第2个峰值大小与出力水平并无单调关系,且低出力水平下的第二峰值可能大于第一峰值。考虑到Crowbar是否动作取决于2个峰值间较大的值,可以绘制出图10(b)中的关系。可见低出力水平下仍可能出现较大的短路电流,这一反常现象与同步机有明显差别。
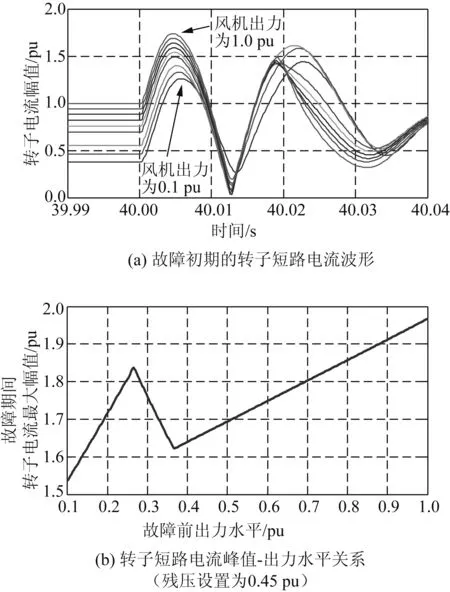
图10 风速分布导致的转子短路电流峰值差异Fig.10 Differences in peak rotor current caused by wind-speed distribution
3 双机等值方案及其关键参数辨识
基于以上分析,本文提出一种“逆向建模”思路,先确定聚合模型的形式(包括等值机台数、连接拓扑),再输入宏观特征参数,然后根据这些特征量反算出各等值机的具体物理参数。在保持风电场关键稳态、动态特性的前提下,通过调整具有物理意义的特征参数来反映目标风电场外部响应由于分布性导致的涨落。宏观特征参数的获取可以按离线方式进行,根据目标风电场的历史数据进行辨识,得到最能体现该风电场内部特征的参数。
3.1 模型基本形式设定
在任意电网外部扰动中,单个风电场内部的发电机都可分成2类:故障期间Crowbar动作的以及故障期间没有动作的。然而,在仿真前并不能预先知道某发电机的Crowbar是否会动作,也不能知道有多少台机组动作,因而需要将该指标进一步转化,建立保护动作与转子短路电流水平间的映射。当整场出力给定时,可以通过合理调整2台等值机的风速来直接调节各自的短路电流,进而拉大或缩小等值机间同调性的差距。
3.2 构造模型的宏观特征参数
输入的宏观特征量应足以反映风电场的关键分布特征,且与风电场数学模型有直观映射关系。该模型需要输入的宏观特征参数为:总出力P、分布性指数λN、差异性指数λS。其中P由风功率预测得到,λN可以反映扰动发生时发电机分群的比例分布,即Crowbar不动作与动作发电机的比例关系;λS反映的是2组发电机短路电流的差异性,可由有功出力水平差异表征。
上述3个参数将最终将映射成2台等值风力发电机中的实际物理量,主要指等值机各自包含的发电机台数和经历的风速。双机聚合模型见图11,假定单台机机械功率与风速间满足关系Pw=Pw(w),2台等值机所包含台数为N1和N2,风速各为w1与w2。首先,忽略发电机自身的损耗,则各物理量间应满足(令N1>N2)
(1)
且台数应满足
N1+N2=N
(2)
式中N为风电场中运行发电机台数。其次,分布性指数λN的定义应满足:N1=N2时λN=1,分布性最大;当N1=N,N2=0时λN=0,分布性最小。据此,本文中假定该特征参数具有如下形式
(3)
当N1确定,由式(1)(2)可以解出2台等值机风速间的函数关系w2(w1)(显然w2是w1的单调减函数),进而得到风速的分布范围。
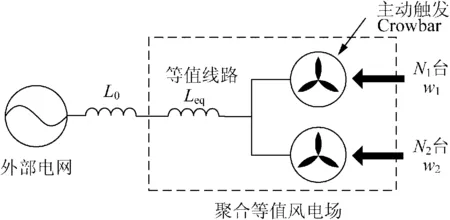
图11 基于逆向建模的风电场双机聚合模型Fig.11 Dual-machine aggregation model based on backward modeling
差异性指数λS的定义应满足,当w1=w2时λS=0,表明出力水平差异性最小;当λS=-1时,w1最小而w2最大,表明差异性最大;当λS=1时,w1最大而w2最小,同样表明差异性最大。据此,本文假定该特征参数λS具有如下形式:
(4)
式中:Mmax(正值)与Mmin(负值)分别为w1/w2-1的最大值和最小值。式中已经对λS进行了归一化。
3.3 宏观特征参数辨识
显然,发电机间的不同调程度与电网侧故障的严重程度有关。例如,发生严重故障时,几乎所有发电机的Crowbar都会动作,此时反映不同调度的宏观特征参数为0。因此,即使对于同一时刻的同一风电场,其参数确定也需要根据该风电场电压跌落深度来进行调整。本文以主变压器低压侧的节点电压作故障程度依据,将该处残压从1~0划分为10个档次,每个档次内认为存在1组最能反映分布性差别的参数配置。当然,得到的参数代入大系统进行计算后,风电场节点残压可能又会发生变化,所以整个仿真过程如图12所示,按照迭代方式进行。
首先,将风电场进行常规单台机等值,代入大系统进行联合计算,得到故障瞬间风电场主变压器低压侧的残压。认为该残压近似各发电机的箱变高压侧电压,将其代入DFIG动态模型,计算出单台机“出力水平-短路电流峰值”曲线,并依据Crowbar动作阈值将曲线划分为保护动作和不动作区域。对该风电场的历史出力录波数据进行扫描,对于所有与总出力吻合的时间点,将该点所有发电机的出力代入程序并确定是否保护动作,并得到Crowbar动作DFIG的总台数和对应的平均出力。
进行扫描后,得到所有时间点上的Crowbar动作台数和平均台数频率分布直方图,得到概率最大的组合。将辨识的台数、平均出力转化为宏观特征参数并输入双机等值模型。将更新后的模型代入大系统重新计算,若此时风电场残压仍位于初次计算的范围内,则结束计算,否则更新残压值,重新进行参数辨识。
4 仿真验证
使用如图13的多机系统验证聚合模型的适用性。风电场WF由20台机组构成,拓扑类型为级联式,共3根馈线,分别馈入8、6和6台DFIG。扰动前风电场出力为0.31 pu。系统内还包含2台同步机SG0和SG1,1个电阻负荷和1个异步电动机负荷IM,故障前稳态潮流分布如图13。SG0代表远端系统,通过联络线L1、L2向本地受端系统送电。
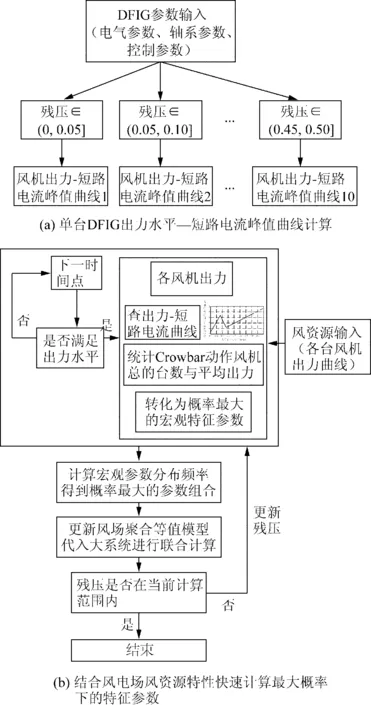
图12 宏观特征参数辨识步骤Fig.12 Identification process of macroscopic characteristic parameters

图13 暂态稳定计算验证所使用的多机系统Fig.13 Multi-node system adopted in transient stability calculation verification
40 s时联络线L1上发生三相短路,300 ms后故障清除。首先,使用常规单机聚合等值模型,计算表明风电场WF主变低压侧电压跌至0.35 pu左右。将此残压值及该风电场的风资源曲线代入如图12(b)的过程,辨识出此时场中Crowbar动作的发电机台数最有可能为11台,如图14。进一步,计算可得到,此时Crowbar动作的所有发电机的最大概率平均出力为0.375 pu,如图15。可得到出聚合模型中台数N1=11,N2=9,等值风速w1=8.73 m/s,w2= 7.68 m/s。按照式(3)、(4)转化为宏观特征参数后输入双机聚合模型,并重新进行暂态稳定计算,发现风电场低压侧残压仍旧位于0.30 ~ 0.35 pu的范围内,表明计算结果已经收敛,辨识出了待设定的宏观特征参数组。

图14 风电场出力为0.35 pu、风电场残压水平为0.31pu时 Crowbar动作发电机台数的分布Fig.14 Number distribution of wind turbines with Crowbar activated (output power of wind farm is 0.35 pu, and residual voltage is 0.31 pu)

图15 Crowbar动作发电机台数为11时的平均出力分布Fig.15 Distribution of average output power when number of wind turbines with Crowbar activated is 11
为了进一步验证双机聚合模型的适应性,仿真WF总出力同样为0.31 pu时该系统的暂态稳定性。图16为该风电场的总出力水平曲线,图中2条线相交处均满足该总出力要求。仿真图中2条曲线相交的各时间点,将各点上各单台发电机出力情况代入详细模型进行暂态稳定计算,分别比较详细模型、常规单机等值以及本文所提出的双机聚合模型。其中使用详细模型时风电场内部确实有11台发电机的Crowbar动作,且该部分发电机的平均出力为 0.39 pu,如图17,这一结果与双机聚合模型中辨识出的结果高度吻合,各发电机呈现出典型的分群趋势。

图16 风电场整场风功率曲线上采样的仿真场景Fig.16 Sampling scenarios selected in the output sequence of wind farm

图17 真实风电场中各台DFIG的功率响应Fig.17 Power response of each DFIG in detailed wind farm
风电场使用单机聚合模型时,Crowbar并未动作,如图18。而真实风电场发生了部分发电机的保护动作,在约40.1 s时该部分发电机Crowbar切出并返回双馈状态,并发生了有功功率的波动,单机聚合模型不能反映该现象,而双机聚合模型可以精确体现这一切换过程导致的波动。无功功率中,单机聚合模型在故障发生起始就发出了相当的无功,而真实风电场在故障发生后的0.10 s内只有9台发电机可以增发无功,另11台反而吸收无功,单机聚合模型计算出的总无功偏高,并导致风电场出口处的电压偏高。
双机聚合模型对真实风电场特性模拟精度的提高可用相邻同步机与异步电动机的暂态稳定性来进一步体现。图19(a)中0.10 s时同步机的电磁功率受制于DFIG中Crowbar切出的影响而出现波动,双机聚合模型对该现象的模拟精度高于常规单机聚合模型。
另外,如上所述,风电场采用单机等值时在故障初始阶段发出的无功高于真实情况,导致相邻异步电动机机端电压与电磁功率偏高,如图19(b)(c)所示。双机聚合模型较单机聚合模型可显著提高暂态稳定计算的精度。

图18 风电场采用不同模型时的动态响应对比Fig.18 Dynamics response comparison of wind farm with different modeling methods

图19 不同风电场模型下相邻发电机与负荷的动态响应Fig.19 Dynamics response of adjacent conventional generator and motor with different modeling methods for the wind farm
5 结 论
(1)本文提出的双机聚合模型可以平滑地改变风电场内部状态,调节分布性水平进而调节暂态过程中因Crowbar动作而短时转为SCIG状态运行的DFIG台数和失控功率比例,从而显著提高聚合模型的精度。
(2)建模中,事先根据风资源特性离线计算一些典型宏观参数组。宏观特征参数同扰动的大小密切相关,须结合电压跌落深度和风电场出力水平辨识最可能的参数组。一般来说,对于严重故障、轻微故障,或风电场出力水平极高、极低,分布性因素造成的发电机间不同调效应低。当故障不太严重或风电场处于中等出力水平时,分布性将显著增大。每个场景下的暂态稳定计算中再根据残压值迭代产生相应的参数组。
(3)本文提出的风电场聚合等值模型,对现有电力电子接口异步电源的建模体系进行了重要改进,可以弥补常规单机等值模型的机理缺陷,体现出由分布式电源组成的电站相对于传统电源的独有特征。此外,该模型一定程度上解决了多机等值方法可操作性低的缺点,在模型复杂度与仿真精度间做到了合理的权衡。
[1]刘斯伟, 李庚银, 周明. 双馈风电机组对并网电力系统暂态稳定性的影响模式分析[J]. 电网技术, 2016, 40(2): 471-476. LIU Siwei, LI Gengyin, ZHOU Ming. Influence mechanism of doubly fed induction generator on power system transient stability [J]. Power System Technology,2016, 40(2): 471-476.
[2]郝正航. 双馈风电机组的暂态行为及其对电力系统稳定性影响[D]. 天津: 天津大学, 2011. HAO Zhenghang. Transient behavior of DFIG and its influence on power system stability [D]. Tianjin: Tianjin University, 2011.
[3]马彦宏, 丁楠, 乔颖. 异步风力发电机组小干扰稳定性机理 [J]. 电力建设, 2013, 34(8): 11-16. MA Yanhong, DING Nan, QIAO Ying. Mechanism of small signal stability of asynchronous wind turbines [J]. Electric Power Construction, 2013, 34(8): 11-16.
[4]徐玉琴, 张林浩, 王娜. 计及尾流效应的双馈机组风电场等值建模研究[J]. 电力系统保护与控制, 2014, 42(1): 70-76. XU Yuqin, ZHANG Linhao, WANG Na. Study on equivalent model of wind farms with DFIG considering wake effects [J]. Power System Protection and Control,2014, 42(1): 70-76.
[5]SLOOTWEG J G, HAANM S. Aggregated modelling of wind parks with variable speed wind turbines in power system dynamics simulations [C]//Power Technology Conference. Bologna, Italy: IEEE, 2003: 1-7.
[6]陈澜, 杨苹, 周少雄, 等. 用于无功补偿的海上风电场等值模型[J]. 电力建设, 2014, 35(7): 126-130. CHEN Lan, YANG Ping, ZHOU Shaoxiong,et al. Equivalent model of offshore wind farms used for reactive power compensation [J]. Electric Power Construction, 2014, 35(7): 126-130.
[7]LIU H, CHEN Z. Aggregated modelling for wind farms for power system transient stability studies [C]//Asia- Pacific Power and Energy Engineering Conference. Shanghai: IEEE, 2012: 1-6.
[8]CHOWDHURY M A, SHEN W X. A novel aggregated DFIG wind farm model using mechanical torque compensating factor [J]. Energy Conversion & Management, 2013, 67(67): 265-274.
[9]葛江北, 周明, 李庚银. 大型风电场建模综述[J]. 电力系统保护与控制, 2013(17): 146-153. GE Jiangbei, ZHOU Ming, LI Gengyin. Review on large-scale wind farm modeling[J]. Power System Protection and Control, 2013(17): 146-153.
[10]AKHMATOV V. Analysis of dynamic behavior of electric power systems with large amount of wind power [D]. Copenhagen: Technical University of Denmark, 2003.
[11]李辉, 韩力, 赵斌, 等. 风电机组等效模型对机组暂态稳定分析结果的影响[J]. 中国电机工程学报, 2008, 28(17) : 105-111. LI Hui, HAN Li, ZHAO Bin, et al.Effect of equivalent models of wind turbines on analysis results of transient stability for wind generator systems [J]. Proceedings of the CSEE, 2008, 28(17) : 105-111.
[12]李东东, 陈陈. 风力发电机组动态模型研究[J]. 中国电机工程学报, 2005, 25(3) :115-119. LI Dongdong, CHEN Chen. A study on dynamic model of wind turbine generator sets [J]. Proceedings of the CSEE, 2005, 25(3): 115-119.
[13]苏勋文. 风电场动态等值建模方法研究[D]. 保定: 华北电力大学, 2010. SU Xunwen. Research on dynamic equivalent modeling of wind farms [D].Baoding: North China Electric Power University, 2010.
[14]李海波, 鲁宗相, 乔颖, 等. 基于非时序生产模拟的风电消纳评估方法[J]. 电力建设, 2015, 36(10): 129-137. LI Haibo, LU Zongxiang, QIAO Ying, et al. Evaluation method of wind power accommodation capacity based on non-sequential production simulation [J]. Electric Power Construction 2015, 36(10): 129-137.
[15]RUAN Jiayang, LU Zongxiang, QIAO Ying, et al. Analysis on applicability problems of the aggregation- based representation of wind farms considering DFIGs’ LVRT behaviors [J]. IEEE Transactions on Power Systems, 2016(pp): 99.
[16]侯佑华, 齐军, 王小海, 等.大规模风电场的建模及其在内蒙古电网安全稳定运行的研究 [J]. 中国电机工程学报, 2010, 30(4): 71-78. HOU Youhua, QI Jun, WANG Xiaohai, et al. Modeling of a large-scale wind farm and the studying for its security and stability operation in Inner Mongolia grid [J]. Proceedings of the CSEE, 2010, 30(4): 71-78.
[17]MARANDI V J, PAK L F, DINAVAHI V. Real-time simulation of grid-connected wind farms using physical aggregation[J]. IEEE Transactions on Industrial Electronics, 2010, 57(9): 3010-3021.
(编辑 蒋毅恒)
A Dual-Machine Aggregation Model of Wind Farm Considering LVRT
GAO Feng1, HUANG Mingyu1, QIAO Ying2, RUAN Jiayang2
(1. State Grid Ningxia Electric Power Research Institute, Yinchuan 750002, China;2.State Key Lab of Power Systems, Department of Electric Engineering, Tsinghua University, Beijing 100084, China)
Due to differences of the relay protection status and external characteristics among generators derived from distribution of the wind speed and collection network, the conventional single-machine aggregation model cannot offer high accuracy of fault ride-through behaviors of real wind farms in all scenarios. This paper proposes a dual-machine model that is more applicable for doubly-fed induction generator (DFIG) wind farms, based on a reverse modeling method and the delicately-designed macroscopic parameters. First, we analyze the effect of over-current protection on controllability of the wind farm. Considering the power-source nature of DFIGs, the Crowbar dynamic during a large disturbance has a great impact on accuracy of the simulated power response, whereas the peak current level decides whether Crowbar is activated. Thus the current level proves to be the critical factor that generates incoherency among DFIGs, based on which the generators can be grouped. Naturally, description of the incoherency can be implemented by a dual-machine model, and its macroscopic parameters can be adjusted according to control parameters and the wind resources, so as to smoothly set the level of distribution factors that produce incoherency. In order to improve practicability of the proposed model, a reliable parameter-identification procedure is presented, which extracts macroscopic parameters reflecting power responses with the maximum probability. Simulation verifies drawbacks of the single-machine aggregation model and performances of the novel model. With the ability to consider features of wind resources, the proposed model remarkably improves accuracy of wind farms’ power modulation behaviors, adjacent synchronous generators’ power-angle dynamics, and the motor-type loads’ voltage dynamics.
dual-machine aggregation model; transient stability; Crowbar effects; low voltage ride through; wind-speed distribution
国网宁夏电力公司科技项目(SGNXDk00BGQ71400076)
TM 71
A
1000-7229(2016)06-0086-10
10.3969/j.issn.1000-7229.2016.06.013
2016-01-14
高峰(1982),男,博士,高级工程师,从事电力系统规划和电力系统分析方面的研究工作;
黄鸣宇(1980),男,硕士,高级工程师,从事电力系统自动化及智能电网工程技术方面的研究工作;
乔颖(1981),女,博士,副教授,研究方向为新能源、分布式发电和电力系统安全与控制;
阮佳阳(1987),男,博士研究生,研究方向为新能源发电机、电站建模和电力系统动态稳定。
