考虑交流电网调节能力的VSC-MTDC改进下垂控制方法

李子寿，周密，徐箭，兰天楷

(1.国网湖北省电力公司，武汉市 430077；2.武汉大学电气工程学院，武汉市 430072)

考虑交流电网调节能力的VSC-MTDC改进下垂控制方法

李子寿1，周密2，徐箭2，兰天楷2

(1.国网湖北省电力公司，武汉市 430077；2.武汉大学电气工程学院，武汉市 430072)

多端柔性直流输电系统的现有下垂控制方法可以将直流网络的不平衡功率在各换流站间进行合理分配，但忽略了各换流站交流侧系统的承受能力，无法根据交流侧系统的暂态响应情况来灵活调节各换流站所分配的不平衡功率量。因此，该文提出一种考虑交流电网调节能力的多端柔性直流网络改进下垂控制方法，该方法根据扰动后交流侧电网的频率偏移情况来自动调节下垂控制的斜率系数，在不改变控制器结构的前提下，可使直流侧的不平衡功率在各交流电网中得到更为灵活合理的分配。在实时数字仿真器(real-time digital simulator, RTDS)平台搭建了仿真模型，通过与固定斜率下垂控制方法和考虑功率裕度的自适应下垂控制方法进行对比，验证了该改进控制方法的有效性和优越性。

多端柔性直流系统；改进下垂控制方法；交流侧响应；频率偏移

0 引 言

随着电力电子技术和现代控制技术的发展，基于可控通断半导体器件(insulated gate bipolar transistor, IGBT)的电压源型换流器(voltage source converter, VSC)在直流输电领域中获得了广泛应用[1]。电压源型换流器所构成的柔性直流(voltage source converter based high voltage direct current, VSC-HVDC)输电网络克服了常规直流输电的固有缺陷，既能实现有功功率和无功功率的解耦控制与直流潮流的快速反转，又能向无源网络供电，非常适合可再生能源的并网和跨区域电网的互联[2-9]。

3个及以上VSC换流站通过串联、并联或混联方式连接起来，构成多端柔性直流(VSC based multi-terminal high voltage direct current, VSC-MTDC)输电网络[10]。目前，VSC-MTDC的基本控制方法主要包括两大类：主从控制方法和带电压下垂特性的控制方法(简称下垂控制)[11-14]。主从控制方法，仅选取1个换流站作为主换流站，采用定直流电压控制，该换流站的作用是维持直流母线电压恒定，并独立承担直流网络中的不平衡功率，相当于交流系统的平衡节点。此方法原理简单，直流电压质量较好，但其要求主换流站具有较大的调节容量，并且需要依靠换流站间的高速通信来协调各换流站有功功率指令值，可靠性差。下垂控制方法则弥补了主从控制方法的缺陷，能够将不平衡功率按照下垂控制中的斜率系数分配至多个换流站，大大减轻了单个换流站的调节压力，且系统正常运行时不需要高速通信，相对可靠。

文献[15]提出一种直流电压偏差控制策略，该策略的实质是在主换流站越限或者退出运行后，具有电压控制能力的后备换流站能够检测到直流电压的较大偏移，并转入定直流电压运行模式，从而接替主换流站维持直流电压的稳定。文献[16]提出了多点直流电压控制策略，将多个换流站设为定直流电压控制模式，提高了多端系统的功率平衡能力和运行的可靠性与经济性。文献[17]和文献[18]在主从控制和下垂控制的基础上，分别设计了基于自律分散思想的组合控制方式和直流电压偏差斜率控制策略，通过两种传统控制方式的组合创新实现了更加可靠灵活的系统控制性能。文献[19]结合直流电压偏差控制和下垂控制的优点，设计了直流电压优化控制策略，优化了系统的动态响应特性。文献[20]设计了一种基于多代理系统的多端直流电网控制系统，并充分利用代理本身的自治性和反应性，获得更迅速、更准确、更优化的多端直流系统控制过程。文献[21]在电压下垂控制中引入一个公共直流参考电压，实现了多点直流电压的协调控制，使系统具有更好的稳态和暂态运行特性。

通常情况下，换流站下垂控制的斜率系数为一个定值，根据换流站的容量来整定，斜率系数一旦确定后，无法根据系统实际运行情况来灵活调节各换流站的功率分配比例。文献[22]提出自适应斜率控制策略，即根据换流站功率裕度来自适应调节斜率系数K，使得不平衡功率在各换流站中得到合理分配。但这种方法完全没有考虑交流电网的承受能力，在实际电网中，分配到各互联电网的不平衡功率不仅与其换流站的功率裕度有关，也应考虑交流侧电网的调节能力。如有些电网虽然与直流侧交换功率较少，换流站功率裕度大，但是其电网当前旋转备用容量很小，若按照文献[22]的分配方法，则在直流电网中出现扰动后，该电网需分摊较多的不平衡功率，交流电网频率将出现过大的偏移。

因此，本文提出考虑交流电网调节能力的VSC-MTDC改进下垂控制方法，在保证直流网络正常工作的前提下，根据扰动后交流侧电网的频率偏移情况来自动调节下垂控制的斜率系数，使得直流侧不平衡功率在各交流电网中得到更为灵活合理的分配。在实时数字仿真器(RTDS)平台搭建三端柔性直流输电网络模型，仿真验证该方法的有效性和优越性。

1 VSC-MTDC的下垂控制方法

适用于VSC-MTDC的直流电压下垂控制原理与交流系统的一次调频原理类似，可以用一条直流电压Udc与有功功率P的下垂特性曲线来表示，如图1所示。由于直流线路上电压降落较小，各换流站直流侧电压近似相等。为了简化分析，本文忽略直流输电线路损耗，认为所有换流站均工作于同一额定直流电压。

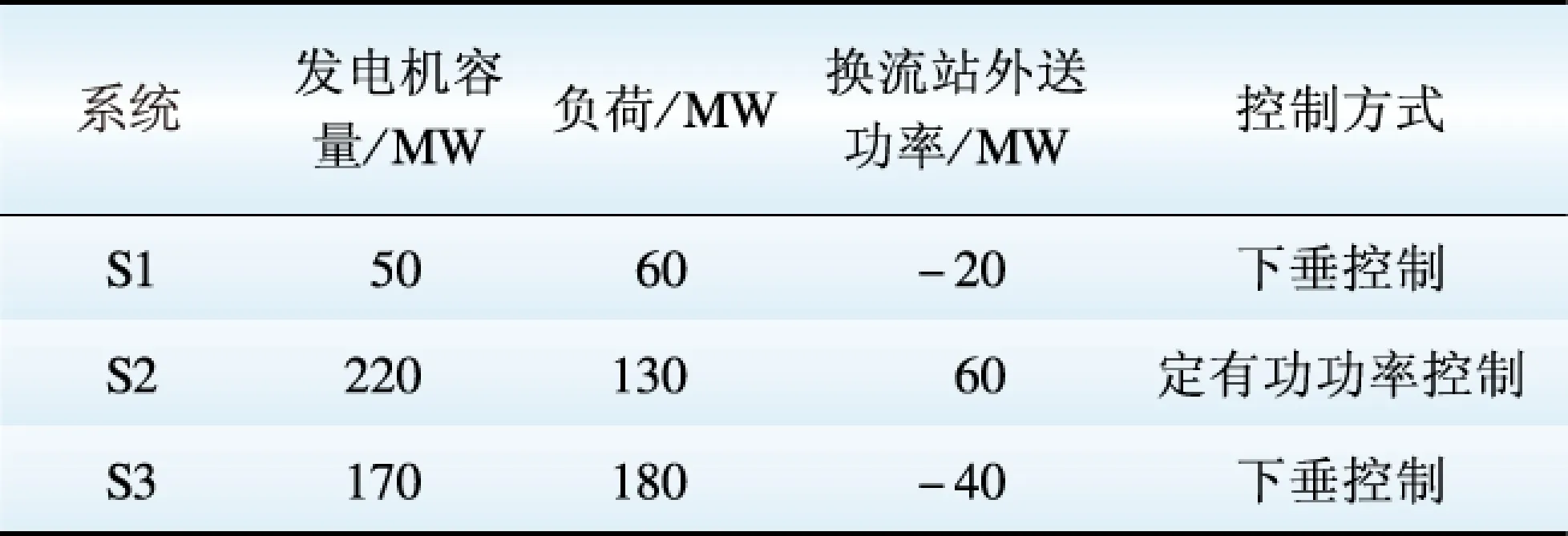
图1 VSC-MTDC下垂控制原理Fig.1 Principle diagram of droop control for VSC-MTDC system

当直流侧出现不平衡功率导致直流电压变化时，各换流站按照斜率系数自动调节其输出的有功功率值，满足直流输电网络的功率平衡，以达到新的稳态。

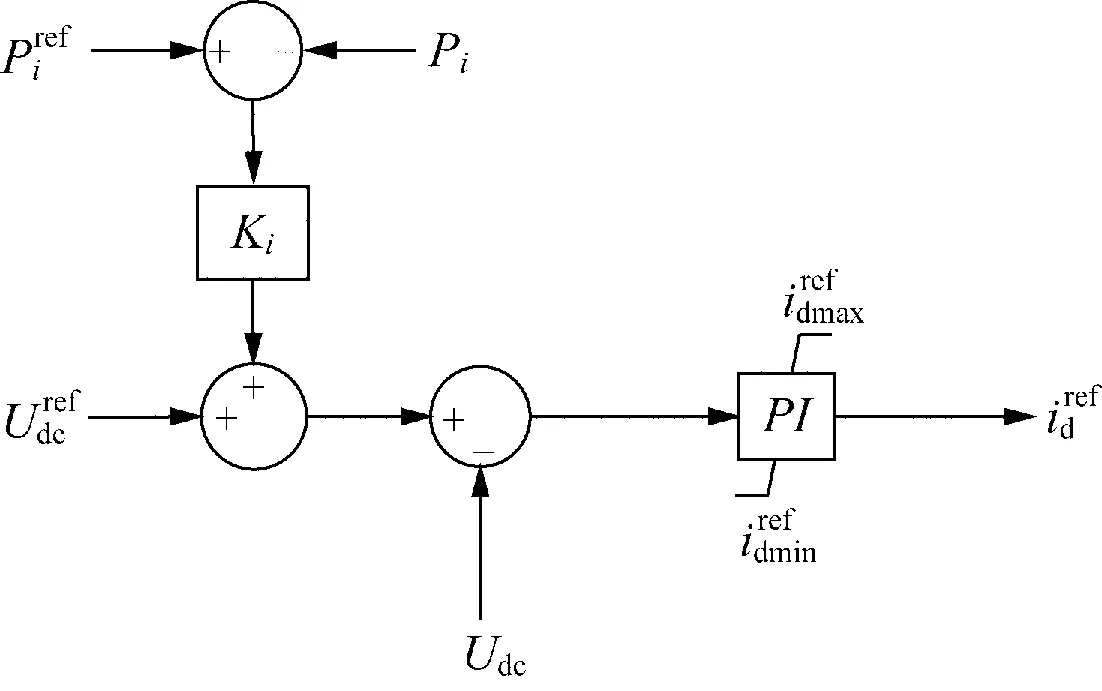
图2 VSC-MTDC下垂控制器结构Fig.2 Structure of droop controller for VSC-MTDC system

稳态时，控制器输出误差信号为0，换流站i直流侧电压与功率的关系可表示为

(1)

当直流网络出现功率扰动ΔP时，直流电压Udc随之改变，各换流站根据其下垂特性自动搜寻新的平衡点。设直流电压的改变量为ΔUdc，则由图1可知，换流站i分摊的有功功率ΔPi与直流电压改变量ΔUdc存在如下关系：

(2)

为了保证直流网络功率平衡，各换流站所分摊的有功功率之和应等于直流网络中的功率扰动值ΔP，故

(3)

即

(4)

将式(4)代入式(2)，换流站i分摊的有功功率量ΔPi可写为

(5)

可以看出，当各换流站的斜率系数固定时，任一换流站在调节过程中所分摊的功率与其斜率系数成反比，即换流站斜率系数越大，其所分摊的不平衡功率越小。通常情况下，各换流站的斜率系数按照其换流站额定容量的反比来整定，保证额定容量大的换流站承担较多的不平衡功率，额定容量小的换流站承担较少的不平衡功率。

2 改进下垂控制方法

采用如前所述的固定斜率下垂控制方法时，未考虑换流站的功率裕度，容易导致个别换流站满载从而失去响应和调节能力。为了克服此缺点，文献[22]提出在暂态过程中根据换流站的功率裕度自动改变各换流站的斜率系数，从而调节其所承担不平衡功率的大小。该方法虽然比固定斜率控制更贴近工程实际，但未考虑到交流电网的实际调节能力。

维持直流网络稳定的根本目的是保证互联交流电网的可靠功率交换及其各自所带负荷的正常运行。直流网络中出现不平衡功率时，若某个换流站功率调节至满载甚至过载而失去了继续响应的能力，其他换流站仍可继续调节，交、直流系统仍能正常运行；但若在平抑不平衡功率的过程中，交流侧系统频率波动过大，容易引起安全稳定控制装置动作，进行切机、切负荷等操作，系统损失较大。故在进行直流网络不平衡功率的协调分配时，应考虑各交流系统的响应及承受能力。

据此，本文提出一种改进的下垂控制方法，其主要目的是在直流电网不平衡功率的分配过程中，考虑交流侧电网的承受和调节能力，根据各交流侧频率波动来调整换流站斜率系数的大小，从而在不改变控制器结构的基础上，使不平衡功率在各互联交流系统中得到更为灵活合理的分配，抑制交流电网频率的过度偏移。

按照上述思路，各换流站的斜率系数可设置为

根据系统不同运行状态，采用此改进控制方法后，换流站可能出现如下3种控制模式：

(2)控制模式2。当直流网络中无功率扰动但某交流侧系统出现扰动时，该交流侧系统所连接换流站的斜率系数Ki会随着其交流频率的波动而改变，但由于直流侧直流电压稳定不变，直流网络的运行点仍在特性曲线的平衡点处，Ki的变化不会影响直流网络的功率分布。换流站输出功率不变，该交流侧频率波动由其交流系统自行调节。

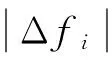
3 仿 真

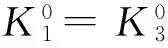
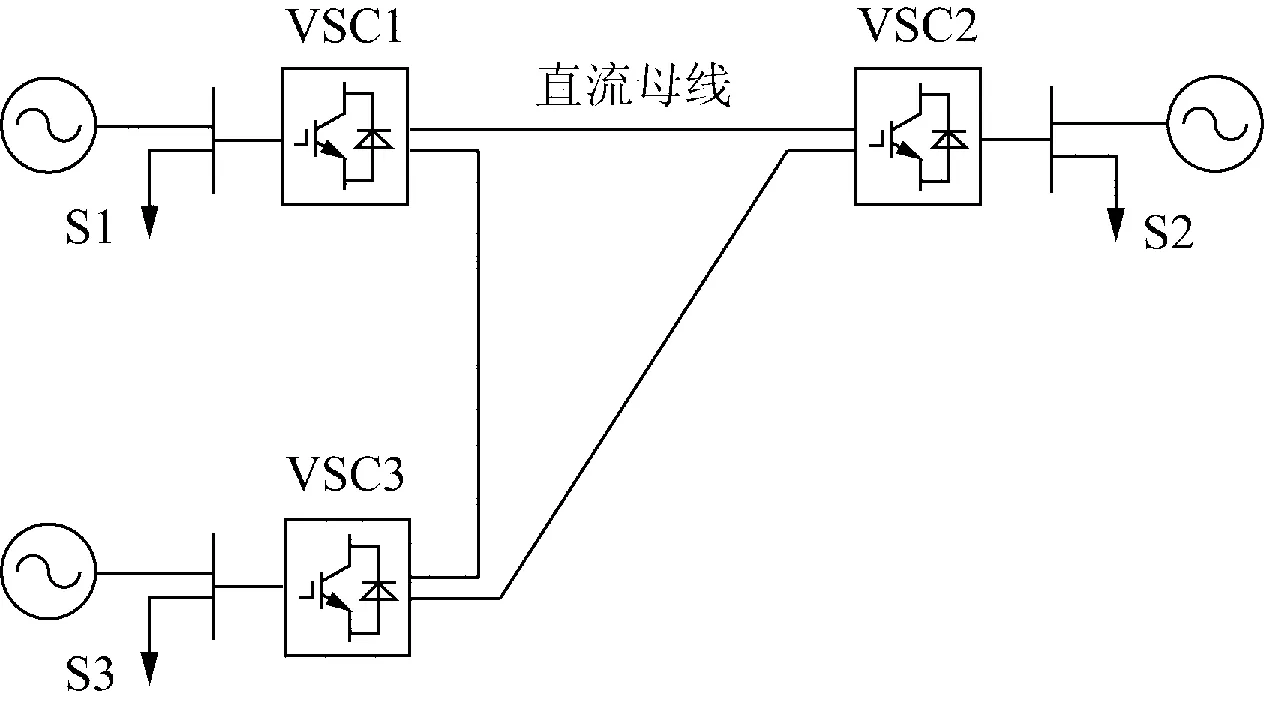
图3 三端柔性直流输电系统仿真结构图Fig.3 Simulation structure of three-terminal VSC-HVDC system表1 三端柔性直流输电系统参数Table 1 Parameters of three-terminal VSC-HVDC system

(1)t=2 s时，换流站VSC2的有功指令值从60 MW提升至70 MW(情况1)。图4和图5分别为各交流系统频率和各换流站外送功率的响应曲线。

如图所示，换流站VSC2的功率指令改变后，若采用固定斜率控制方法，直流侧10 MW的不平衡功率按照固定的斜率在系统S1和S3间进行分配，即PVSC1和PVSC3各增加5 MW，f1和f3分别向上波动至50.43 Hz和50.12 Hz。

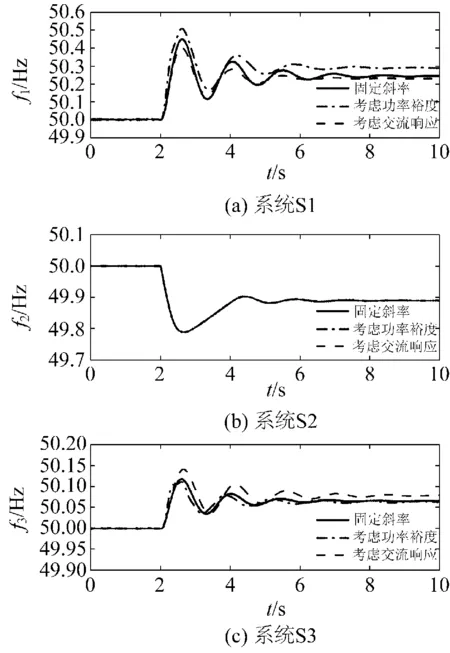
图4 交流侧系统频率响应曲线(情况1)Fig.4 Frequency response curves of AC systems (case 1)

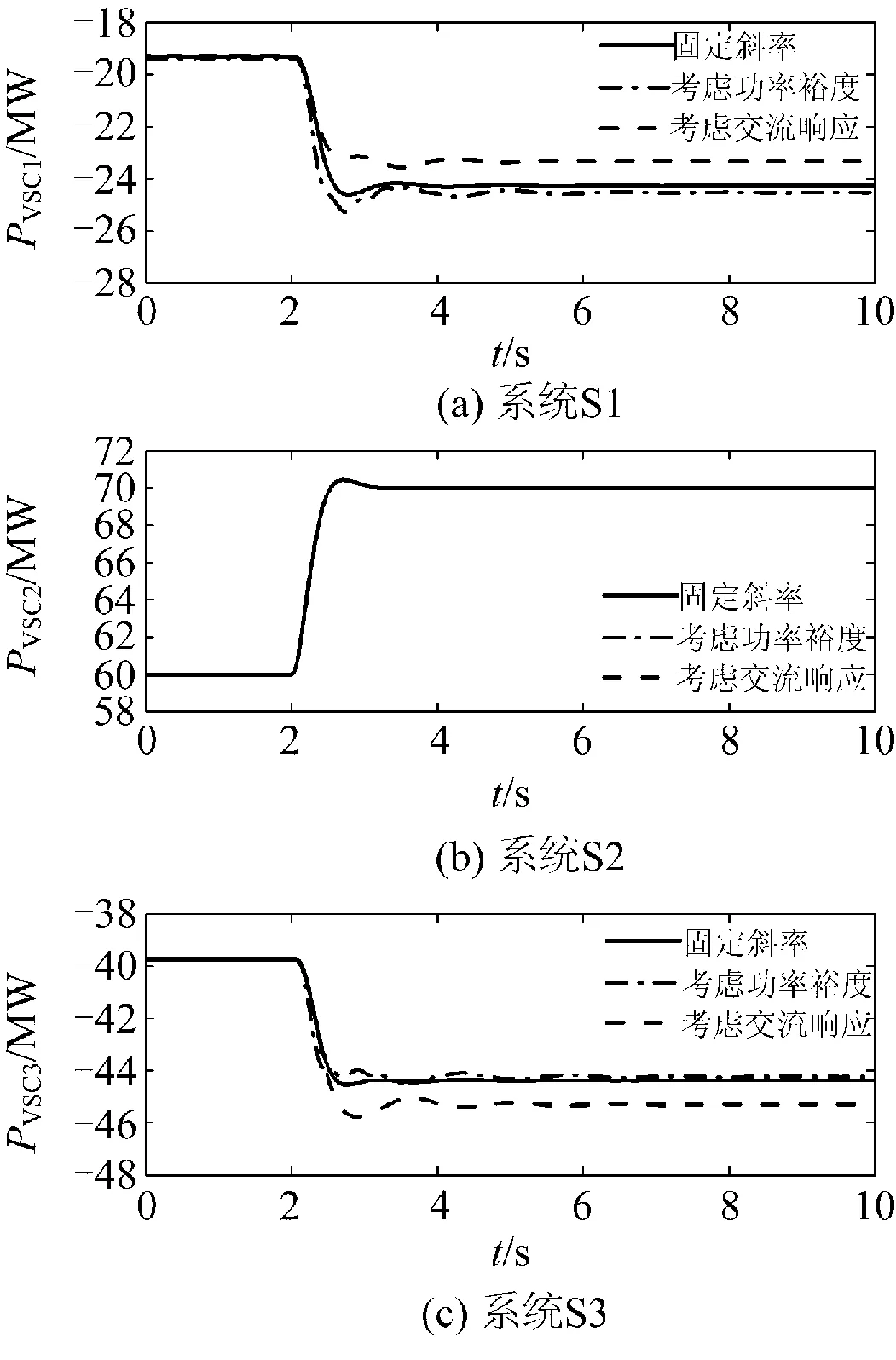
图5 换流站外送功率响应曲线(情况1)Fig.5 Power output response curves of converter stations (case 1)

如果采用文献[22]中考虑换流站功率裕度的下垂控制方法，由于在扰动后换流站VSC1的功率裕度计算值较大，交流系统S1需承担较多不平衡功率，VSC1外送功率PVSC1的改变量增加，VSC3的外送功率PVSC3的改变量减少。与定斜率控制时相比，f3的波动稍有减弱；但由于系统S1装机容量小、调节能力弱，频率f1波动峰值为50.51 Hz，大于定斜率控制时的峰值，且超过了电网频率的安全稳定范围。

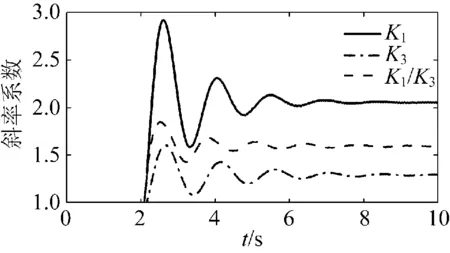
图6 斜率系数K变化曲线(情况1)Fig.6 Response curves of the droop coefficients Ki (case 1)

(2)t=2 s时，VSC2的有功指令值从60 MW降至55 MW(情况2)。图7、8分别为各交流系统频率和各换流站外送功率的响应曲线。

t=2 s时，VSC2的有功指令值从60 MW降至55 MW，直流侧出现-5 MW的不平衡功率，若采用定斜率控制方法，PVSC1和PVSC3各减少-2.5 MW，频率f1和f3最低分别降至49.78 Hz和49.94 Hz。

如采用考虑换流站功率裕度的控制方法，换流站VSC1的功率裕度计算值较VSC3的小，交流系统S1承担较少的不平衡功率，交流系统S3承担较多的不平衡功率。与定斜率控制时相比，f1波动的最低值提升至49.82 Hz，f3波动的最低值降至49.93 Hz。

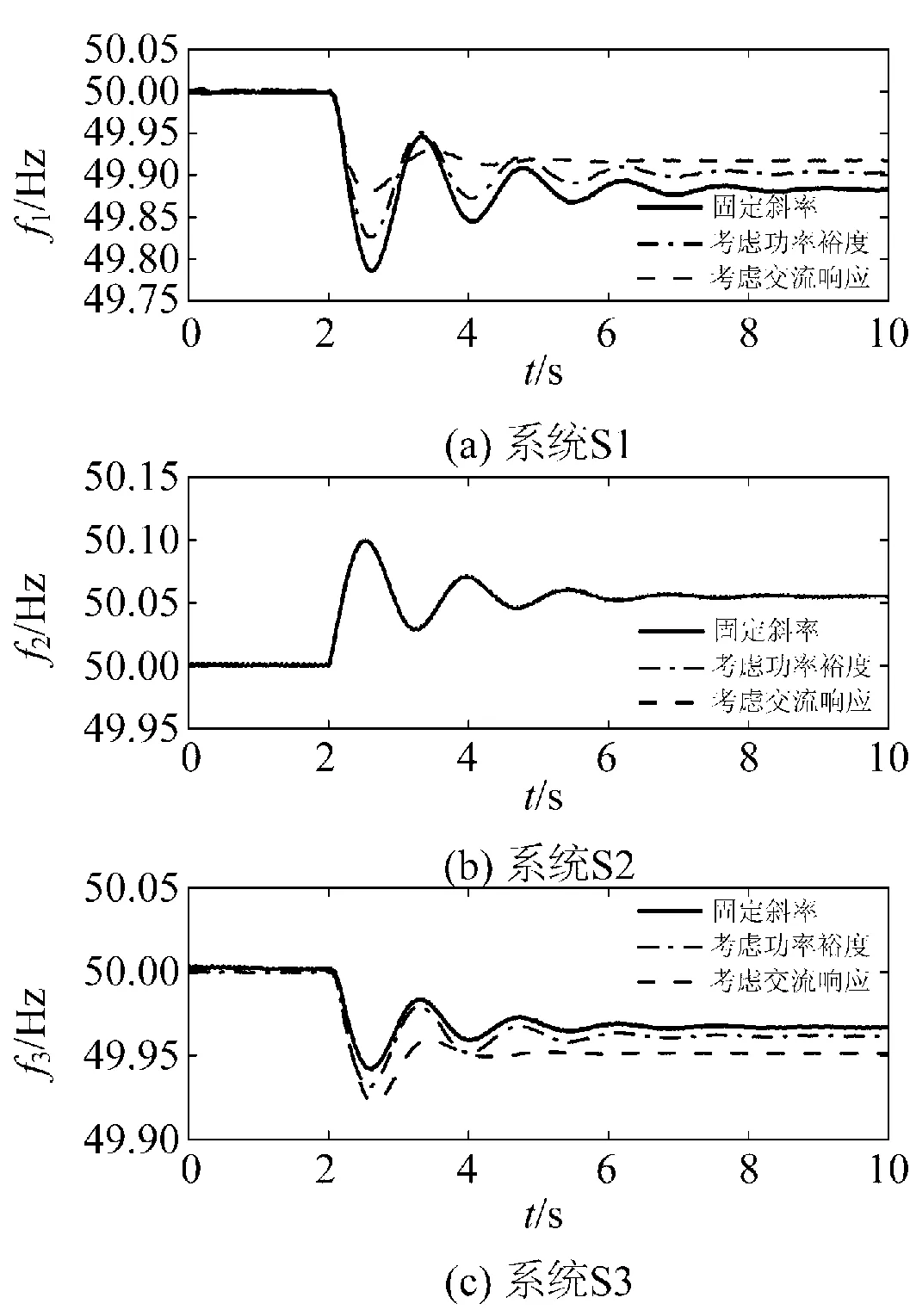
图7 交流侧系统频率响应曲线(情况2)Fig.7 Frequency response curves of AC systems (case 2)

图8 换流站外送功率响应曲线(情况2)Fig.8 Power output response curves of converter stations (case 2)

(3)t=2 s时，换流站VSC1交流母线节点1处发生瞬时性单相接地故障，短路时间为0.1 s，短路阻抗为1 Ω(情况3)。

如图10、11所示，t=2 s后，短路故障导致VSC1交流侧母线电压UBUS1陡降，换流站VSC1吸收的功率迅速减少。为保证直流网络的功率平衡，VSC3吸收的功率增加。

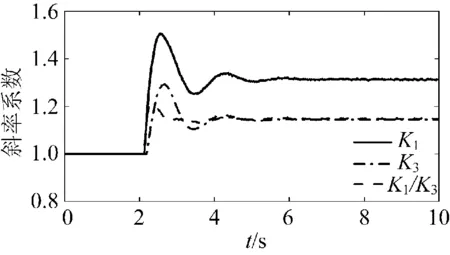
图9 斜率系数K变化曲线(情况2)Fig.9 Response curves of slope coefficients Ki (case 2)

图10 交流系统S1交流侧电压响应曲线Fig.10 AC voltage response curves of system S1

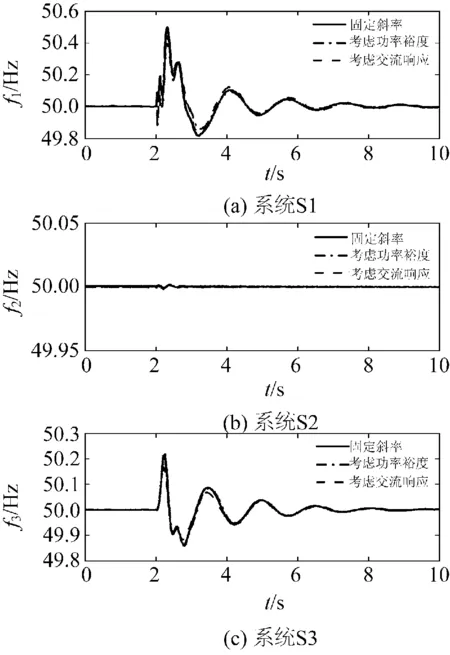
图11 交流侧系统频率响应曲线(情况3)Fig.11 Frequency response curves of AC systems (case 3)

若斜率系数固定不变，频率f1在故障消除后波动至50.50 Hz。若采用所提出的改进控制方法，由于分摊至各换流站的不平衡功率能够快速地响应交流系统频率的暂态变化，最终f1最高波动至50.40 Hz，其控制效果优于固定斜率和考虑换流站功率裕度的控制方法。

由于不平衡功率在各系统间得到了更为合理的分配，直流电压波动被快速平抑，如图12所示，f3的偏移也更小。

图12 直流电压响应曲线Fig.12 DC voltage response curves

由3组仿真结果可知，若采用所提出的改进下垂控制方法，在VSC-MTDC中互联交流系统的总调节能力充足的情况下，各端系统的频率偏移均不会超出标准运行范围。在暂态变化过程中，一旦有某端系统的频率偏移过大，其对应换流站的输送功率将朝着抑制其频率继续偏移的趋势改变，而其他频率偏移较小的交流系统所对应换流站的输送功率将朝着使其系统频率偏移增大的趋势改变。最终，VSC-MTDC中的不平衡功率在各端系统间得到了更为合理的分配，各系统的频率偏移趋于平均，均不会超过标准范围。

4 结 论

VSC-MTDC系统采用故定斜率的下垂控制方法时，直流网络中的不平衡功率将按照既定斜率在各换流站间进行分配，未考虑实际运行工况，更没有考虑交流系统的响应及承受能力，可靠性较差。据此，本文提出一种考虑交流电网调节能力的VSC-MTDC改进下垂控制方法，当直流网络出现功率扰动时，该改进控制方法能够根据交流电网的频率响应情况来灵活地调节各换流站的斜率系数，进而改变各互联系统所承担的不平衡功率，提高交流电网的稳定性，使系统更快达到稳态。RTDS仿真结果验证了该方法在不同运行情况下的正确性和有效性。

[1]林海雪，汤广福，贺之渊.灵活电力传输：HVDC的选择[M].北京：中国电力出版社，2010：76-90.

[2]胡航海，李敬如，杨卫红，等.柔性直流输电技术的发展与展望[J].电力建设，2011，32(5)：62-66. HU Hanghai，LI Jingru, YANG Weihong，et al.The development and prospect of HVDC flexible technology[J].Electric Power Construction，2011，32(5)：62-66.

[3]汤广福，贺之渊，庞辉.柔性直流输电工程技术研究、应用及发展[J].电力系统自动化，2013，37(15)：3-14. TANG Guangfu，HE Zhiyuan，PANG Hui.Research, application and development of VSC-HVDC engineering technology[J].Automation of Electric Power Systems，2013，37(15)：3-14.

[4]张勇军，陈碧云.高压直流输电原理与应用[M].北京：清华大学出版社，2012：271-277.

[5]徐政，陈海荣.电压源换流器型直流输电技术综述[J].高电压技术，2007，33(1)：1-10. XU Zheng，CHEN Hairong.Review and applications of VSC-HVDC[J].High Voltage Engineering，2007，33(1)：1-10.

[6]侯慧，游大海，尹项根.轻型高压直流输电技术的发展与应用[J].电力建设，2005，26(11)：28-30. HOU Hui，YOU Dahai，YIN Xianggen.Development and application of light HVDC transmission technique[J].Electric Power Construction，2005，26(11)：28-30.

[7]朱晓东，周克亮，程明，等.大规模近海风电场VSC-HVDC并网拓扑及其控制[J].电网技术，2009，33(18)：17-24. ZHU Xiaodong，ZHOU Keliang，CHENG Ming，et al.Topologies and control of VSC-HVDC systems for grid-connection of large-scale offshore wind farms [J].Power System Technology，2009，33(18)：17-24.

[8]梁海峰，李庚银，李广凯，等.向无源网络供电的 VSC-HVDC 系统仿真研究[J].电网技术，2005，29(8)：45-50. LIANG Haifeng，LI Gengyin，LI Guangkai，et al.Simulation study of VSC-HVDC system connected to passive network[J].Power System Technology，2005，29(8)：45-50.

[9]黄珂.柔性直流输电在辽宁电网中的应用研究[D].北京：华北电力大学，2014. HUANG Ke.Research on VSC-HVDC using in Liaoning power grid[D].Beijing：North China Electric Power University，2014.

[10]汤广福，罗湘，魏晓光.多端直流输电与直流电网技术[J].中国电机工程学报，2013，33(10)：8-17. TANG Guangfu，LUO Xiang，WEI Xiaoguang.Multi-terminal HVDC and DC-grid technology [J].Proceedings of the CSEE，2013，33(10)：8-17.

[11]阮思烨，李国杰，孙元章.多端电压源型直流输电系统的控制策略[J].电力系统自动化，2009，33(12)：57-60. RUAN Siye，LI Guojie，SUN Yuanzhang.A control strategy for multi-infeed VSC-HVDC systems [J].Automation of Electric Power Systems，2009，33(12)：57-60.

[12]李程昊，詹鹏，文劲宇，等. 适用于大规模风电并网的多端柔性直流输电系统控制策略[J].电力系统自动化，2015，39(11)：1-7. LI Chenghao，ZHAN Peng，WEN Jinyu，et al. A multi-terminal VSC-HVDC system control strategy for large wind farms integration[J].Automation of Electric Power Systems，2015，39(11)：1-7.

[13]阎发友，汤广福，贺之渊，等.基于MMC的多端柔性直流输电系统改进下垂控制策略[J].中国电机工程学报，2014，34(3)：397-40. YAN Fayou，TANG Guangfu，HE Zhiyuan，et al.An improved droop control strategy for MMC-based VSC-MTDC systems[J].Proceedings of the CSEE，2014，34(3)：397-40.

[14]陈谦.新型多端直流输电系统的运行与控制[D].南京：东南大学，2005. CHEN Qian.Operation and control of VSC based multi-terminal HVDC [D].Nanjing：Southeast University，2005.

[15]陈海荣，徐政.适用于VSC-MTDC系统的直流电压控制策略[J].电力系统自动化，2006，30(19)：28-33. CHEN Hairong，XU Zheng.Novel DC voltage control strategy for VSC based multi-terminal HVDC system [J].Automation of Electric Power Systems，2006，30(19)：28-33.

[16]陈海荣.基于VSC的多端直流输电系统的控制策略[J].电力建设，2011，32(8):58-63. CHEN Hairong.Control strategy of VSC based multi-terminal HVDC system [J].Electric Power Construction，2011，32(8):58-63.

[17]熊凌飞，韩民晓.基于组合方式的多端柔性直流输电系统控制策略[J].电网技术，2015，39(6)：1586-1592. XIONG Lingfei，HAN Minxiao.A novel combined control strategy for VSC-MTDC[J].Power System Technology，2015，39(6)：1586-1592.

[18]唐庚，徐政，刘昇，等.适用于多端柔性直流输电系统的新型直流电压控制策略[J].电力系统自动化，2013，37(15)：125-132. TANG Yu，XU Zheng，LIU Sheng，et al.A novel DC voltage control strategy for VSC-MTDC systems[J].Automation of Electric Power Systems，2013，37(15)：125-132.

[19]吕金历，王毅，王纯，等.多端柔性直流输电系统的直流电压优化控制策略[J].现代电力，2014，31(6)：15-21. LV Jinli，WANG Yi，WANG Chun，et al.A DC voltage optimal control strategy for VSC-MTDC systems [J].Modern Electric Power，2014 ，31(6)：15-21.

[20]吴俊宏，艾芊，章健，等.基于多代理技术的VSC-MTDC控制系统[J].电力系统自动化，2009，33(19)：85-89. WU Junhong，AI Qian，ZHANG Jian，et al.A VSC-MTDC control system based on multi-agent technology[J].Automation of Electric Power Systems，2009，33(19)：85-89.

[21]阎发友，马巍巍，朱琳，等.多端柔性直流输电系统新型直流电压控制策略[J].智能电网，2013，1(2)：17-21. YAN Fayou，MA Weiwei，ZHU Lin，et al.A novel DC voltage control strategy for multi-terminal VSC-HVDC system[J].Smart Grid，2013，1(2)：17-21.

[22]朱瑞可，王渝红，李兴源，等.VSC-MTDC系统直流电压自适应斜率控制策略[J]. 电力系统自动化，2015，39(4)：63-68. ZHU Ruike，WANG Yuhong，LI Xingyuan，et al.An adaptive DC voltage droop control strategy for the VSC-MTDC system[J]. Automation of Electric Power Systems，2015，39(4)：63-68.

[23]汤广福.基于电压源换流器的高压直流输电技术[M].北京：中国电力出版社，2010.

[24]陈慈萱. 电气工程基础[M].北京：中国电力出版社，2004.

(编辑 张小飞)

An Improved Droop Control Method for VSC-MTDC Considering AC Grid Regulation Ability

LI Zishou1, ZHOU Mi2, XU Jian2, LAN Tiankai2

(1.State Grid Hubei Electric Power Company, Wuhan 430077, China；2. School of Electrical Engineering,Wuhan University, Wuhan 430072, China)

The existing droop control methods for the voltage source converter based multi-terminal high voltage direct current (VSC-MTDC) system can reasonably distribute the unbalanced power of DC network among the converter stations, but neglect the bearing capacity of AC system in converter system, and cannot flexibly adjust the power output variation of converter stations according to the transient responses of the AC systems. Therefore, this paper proposes an improved droop control method for VSC-MTDC system considering the adjusting ability of AC grid. The improved method can adaptively modify the slope coefficient of droop control based on the frequency deviation of the AC grid, which can distribute the unbalance power in the DC grid more flexible and reasonable without changing the controller structure. Compared to the droop control method with fixed slope coefficient and the adaptive droop control method with considering power margin, the proposed improved control method is proved to be more effective and superior on the RTDS (real-time digital simulator) platform.

VSC-MTDC; improved droop control method; response of AC system; frequency deviation

国家重点基础研究发展计划项目(973计划)(2012CB215201)；国家自然科学基金项目(51477122，51190100)

TM 727

A

1000-7229(2016)06-0079-07

10.3969/j.issn.1000-7229.2016.06.012

2016-02-20

李子寿(1979)，男，硕士，主要从事电力系统运行与控制方面的研究；

周密(1991)，女，通信作者，硕士研究生，主要研究方向为电力系统稳定分析与运行控制，柔性直流输电与直流电网控制；

徐箭(1980)，男，博士，副教授，主要研究方向为电力系统暂态稳定、电压稳定分析与控制，大规模风电并网分析与控制等;

兰天楷(1994)，男，湖北武汉人，本科在读，主要研究方向为电力系统运行与控制。

Project supported by The National Basic Research Program of China (973 Program)(2012CB215201);National Natural Science Foundation of China(51477122,51190100)