含风电电力系统经济调度Wait-and-See模型的对比分析

黎静华，朱敦麟，潘毅

(1.广西电力系统最优化与节能技术重点实验室(广西大学)，南宁市 530004；2.中国电力科学研究院，北京市 100192)

含风电电力系统经济调度Wait-and-See模型的对比分析

黎静华1，朱敦麟1，潘毅2

(1.广西电力系统最优化与节能技术重点实验室(广西大学)，南宁市 530004；2.中国电力科学研究院，北京市 100192)

为了更好地选择计及风电随机特性的电力系统调度计划模型，引入了3种基于风电场景的经济调度wait-and-see模型进行对比分析。从目标函数入手，对比分析“尽可能接近风电均值”和“调度计划调整量最小”这2种目标函数的差异。基于功率平衡方程，推导了3种模型制定的调度计划在应对实际可能发生的风电场景时的调节能力以及调整幅度，并进行了对比分析。最后，以IEEE 24节点系统为仿真算例，从运行成本、调节能力、调整幅度、弃风量等方面，对3种模型的仿真结果进行对比分析。分析结果表明：以调整量最小为目标的模型在鲁棒性、经济性、计算速度等方面相对于其他两个模型具有明显优势。所提供的3种经济调度模型以及对比分析结果可为运行人员灵活选择含有风电的电力系统调度计划优化模型提供参考。

wait-and-see模型；经济调度；调度计划；风电场景；随机特性

0 引 言

随着大规模风电的并网，其随机性、间歇性对电力系统运行调度的影响不可忽视[1]，计及风电随机特性的电力系统经济调度计划的制定成为当前调度运行部门的一项工作难点。

迄今，考虑风电随机特性的电力系统经济调度问题已得到较为广泛且深入的研究。总体而言，计及风电随机特性的电力系统经济调度模型主要可分为2类：here-and-now(直觉)模型[2-7]和wait-and-see(静观)的模型[8-12]。here-and-now模型主要是将风电的随机特性以概率约束或均值目标函数的形式在模型中体现，基本思想是采用“该约束可以被满足的概率大于给定阀值”的概率函数形式表示含有风电出力的约束，或者将“运行费用的均值”作为目标函数。here-and-now模型可以较为准确地反映风电出力的随机特性，然而，概率函数或均值函数的解算是难点。与here-and-now相比，wait-and-see模型则是将风电直接作为随机变量体现在经济调度模型中。场景法是解算wait-and-see模型的主要方法，近年来已有不少文献对风电场景的生成展开研究[13]。由于经济调度wait-and-see模型解算简单，易于实现，得到了广泛的使用。因此，本文针对常见的经济调度wait-and-see模型进行对比分析，为调度运行人员灵活选择模型提供参考。

实际运行中，衡量调度计划制定模型的性能主要包含：调度计划的调节能力，调度计划在实际运行中的调整量，调度计划的经济性以及模型的计算复杂度。通常认为，好的调度计划制定模型具有强的调节能力、调度计划在实际运行中需要的调整量小、经济性好且计算简单。然而，这些因素是相互制约的，需要建立优化模型进行协调优化。当前，常见的含风电电力系统经济调度wait-and-see优化协调模型主要有：(1)在目标函数中对风电的计划出力与风电均值的偏差进行惩罚，风电的计划出力作为随机变量体现在约束中(以下称模型A)[14-18]；(2)采用表征风电随机特性的场景替换风电随机变量，生成能满足多种风电场景的鲁棒经济调度计划(以下称模型B)[19-22]；(3)在上述两种模型的基础上，生成的一种以最小调整量满足所有风电代表场景的调度计划(以下称模型C)[23]。不同的调度模型，其特点和意义不同，容易给电力调度人员选择模型造成困难。为了能更好地了解和区别常见的含风电电力系统经济调度wait-and-see模型，方便调度运行人员灵活选择所需的调度计划制定模型，本文分别从运行成本、调节能力、调整幅度以及计算量等方面，对上述3种模型的性能进行对比分析。最后，以IEEE 24节点为算例，对各模型的性能进行对比。

1 电力系统经济调度的运行约束

1.1 系统功率平衡约束

功率平衡约束指的是系统机组的出力必须等于系统负荷与网络的损耗之和，在不计及网损的情况下，系统的功率平衡方程表示为

(1)

1.2 旋转备用约束

旋转备用是将所有运行机组的最大出力之和减去当前系统的负荷和损耗。传统的电力系统备用主要是为了保证系统可靠供电的一项重要措施，防止当出现1台机组或几台机组故障时，系统出现严重的负荷缺额从而导致系统频率急剧下降而发生故障。而在含新能源的电力系统中，旋转备用的配置主要有2个功能：

(1)提供调节容量以弥补负荷预测和新能源预测的不准确所引起的负荷和新能源出力的偏差。

(2)当出现大型发电机组发生故障时，迅速将负荷转移到系统的其他机组。

旋转备用约束主要包含正旋转备用约束和负旋转备用约束2类。

正旋转备用约束可表示为

(2)

负旋转备用约束可表示为

(3)

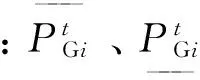
1.3 爬坡速率约束

爬坡约束速率指的是机组i在单位时间(1min)内可以增加或减小的出力，其中机组单位时间内可以增加的出力称为上坡速率(ramp-up)，反之称为下坡速率(ramp-down)。具体表示可表示为

(4)

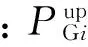
1.4 机组出力约束

机组的出力必须小于或等于其允许的最大出力，大于或等于其允许的最小出力，即

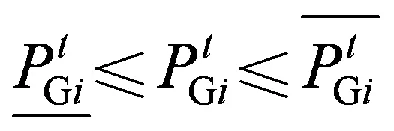
(5)

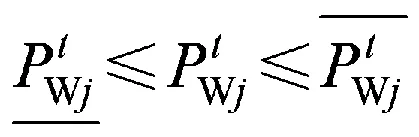
(6)

2 经济调度wait-and-see模型

2.1 模型A

2.1.1 目标函数

模型A的目标函数包括系统总运行费用和惩罚费用2个部分，如式(7)所示。惩罚费用是对风电出力计划偏离风电均值部分的惩罚，包括高于风电均值和低于风电均值惩罚两个部分。从目标函数可以看出，模型A所得的调度计划是使得风电的出力尽可能地接近其均值。

(7)

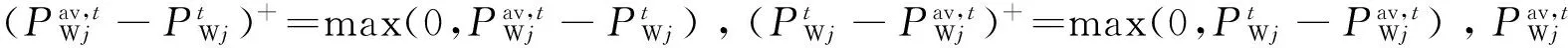
(8)

式中：ai、bi和ci为第i台常规机组运行费用的2次、1次和0次费用。

2.1.2 约束条件

模型A的约束条件包括式(1)—式(6)。

2.2 模型B

2.2.1 目标函数

模型B的目标函数包括运行成本费用FC和惩罚费用2个部分，运行成本的计算公式与式(8)相同，惩罚费用是对为了满足所有风电代表场景，调度计划所需做出的调整量的惩罚。从目标函数来看，模型B是为了制定能以最小调整量应对所有风电代表场景的调度计划。

(9)

2.2.2 约束条件

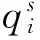
(10)

(11)

(2)其他约束。模型B的其他约束如式(2)—式(6)所示。

2.3 模型C

2.3.1 目标函数

(12)

2.3.2 约束条件

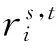
(13)

(2)其他约束。模型C的其他约束如式(2)—式(6)所示。

3 模型的对比分析

为了清楚地认识上述3种模型的特点，本节从调度计划的特点、调节能力等方面分别进行对比分析。

3.1 调度计划特点

模型A所得的调度计划是尽可能接近风电场预测出力均值的计划，所得调度计划主要是针对满足风电均值一种场景，鲁棒性较弱。

3个模型的特点归纳如表1所示。相对于模型A，模型B和模型C则要求调度计划通过适当的调整可以满足所有给定的风电场景，且以调整量最小为目标函数。但从模型B的功率平衡约束看，其常规机组的出力之和限定为预测负荷减去风电场出力的均值。而模型C不做此限定，因此从这一角度来说，模型C的鲁棒性比模型B更强。

表1 3种模型的特点对比

Table 1 Characteristic comparison of three models

3.2 常规机组的调节能力

。

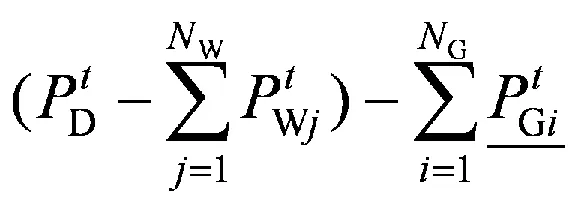
从3个模型的调节能力来看，模型B的调度计划的调节能力由风电的出力均值决定，其调节能力是固定的，灵活性较差。当风电的实际出力偏离均值较大时，可能会引起调节能力不足。模型A的调节能力稍强，但结合目标函数来看，与模型B接近，模型A的调度计划的目标也是尽可能接近风电出力均值。相比模型A和模型B，模型C的调度计划可满足所有给定的场景，因此，调节能力更强，灵活性更好。

4 仿真计算

为了验证上述模型的特点，以IEEE 24节点系统为算例，分别对上述3种模型进行仿真计算。并从调度计划、调节量、目标函数等方面，对比分析3种模型的性能。

4.1 仿真说明

IEEE 24节点系统为包括12台机组和1个风电场，系统机组参数如下表2所示。其中，Ai，Bi，Ci为机组发电成本函数系数，Pmax，Pmin表示机组出力上下限，Ru为机组爬坡率。

表2 IEEE 24节点机组参数

Table 2 Parameters of IEEE 24 node unit

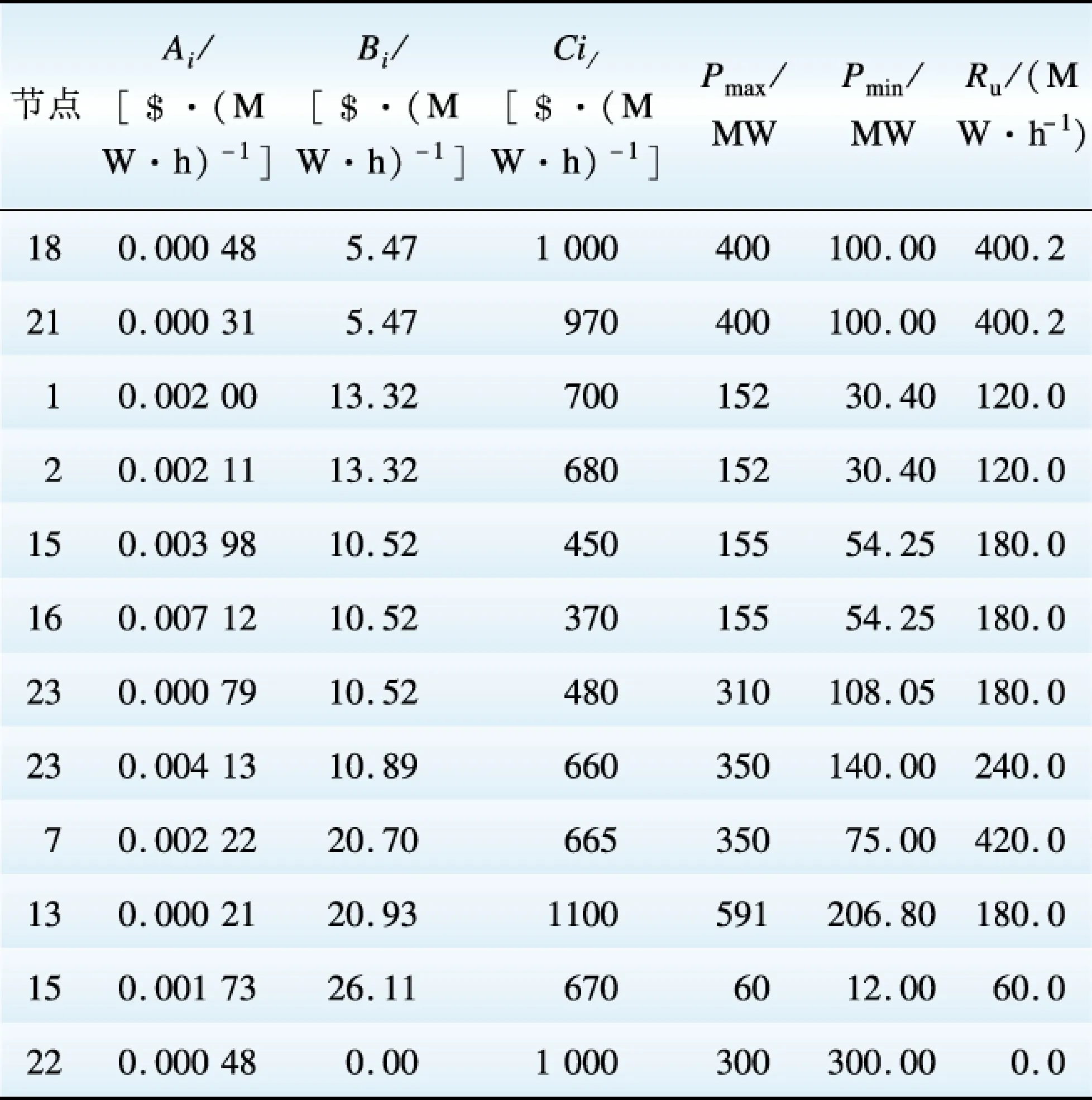
系统总装机容量4 065 MW，其中风电装机容量为690 MW，占总装机容量的17.25%。分别取Cp=50$/(MW·h),Cb=50$/(MW·h),Cq=50$/(MW·h),Cr=50$/(MW·h),Cv=60$/(MW·h)[23]。选取1天内 24 h时段进行仿真计算，系统24时段负荷曲线见图1。

图1 24时段负荷曲线Fig.1 Load curve of 24-hour time period

4.2 场景集

通过随机模拟和场景削减技术[24]产生多个风电预测场景集，如图2所示为生成的22个风电场景值，观察图形可知场景值数量多，呈现起伏的山群状，其范围囊括风电出力预测均值，具有很强的代表性。将所生成的风电预测场景值分别带入模型B和模型C中，得到如图2所示仿真结果。

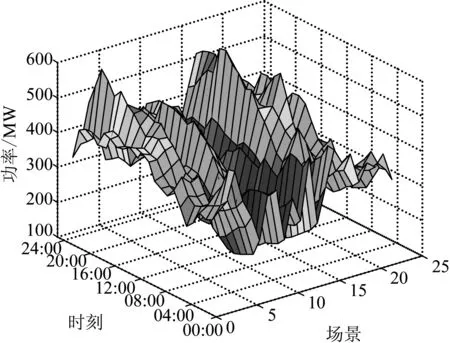
图2 22个预测风电场景值Fig.2 22 predicted scenarios of wind power

4.3 仿真结果

如图3所示为3种模型调度计划柱状图，其中每个柱子表示某时段所有机组出力之和，由图3可知，模型B与模型C调度计划较为接近，模型A调度计划于09：00—21：00时段处低于模型B和模型C。

如图4所示为3种模型实际风电出力及调度计划曲线，其中风电实际出力为负荷功率与机组总出力之差。

由图4可知，模型A所得实际风电出力接近风电功率均值，而模型B和模型C实际风电出力与预测均值相差较大，其原因在于模型B和模型C为应付所有风电功率场景值，对机组出力进行了调整。

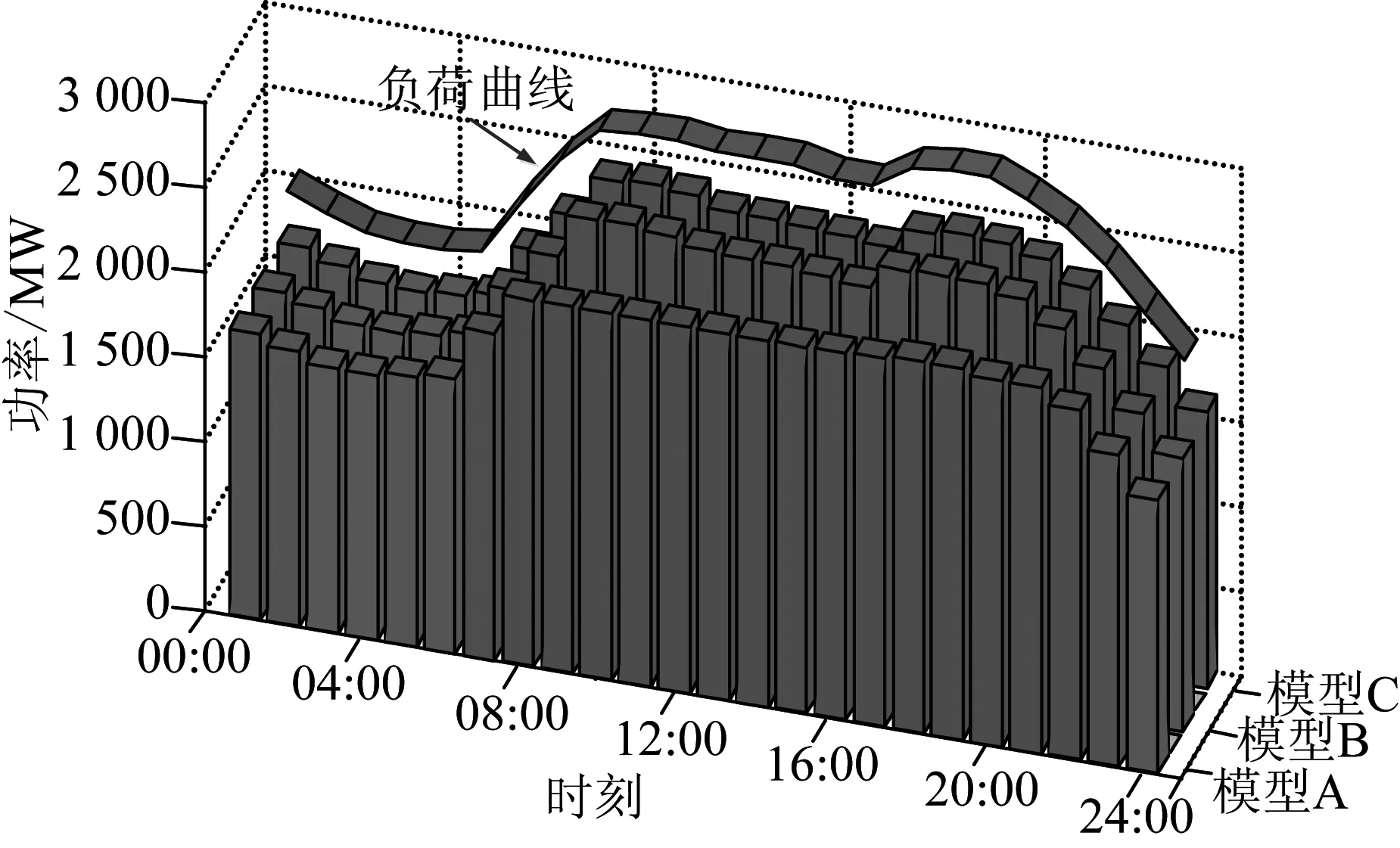
图3 3种模型调度计划对比Fig.3 Comparison of dispatching plans in three models

图4 风电及负荷曲线Fig.4 Wnd power and load curves

其中，各模型实际风电出力以及预测风电出力均值如表3所示，由表可知，模型A的实际风电出力尽可能地接近了预测风电出力均值，由表3数值以及图4曲线可以看出模型B和模型C在09：00—20：00时段把机组出力调高，以满足负荷高峰以及风电场出力偏离预测均值较大的情况。

表3 3种模型的风电出力

Table 3 Wind power output of three models MW

4.4 经济性分析

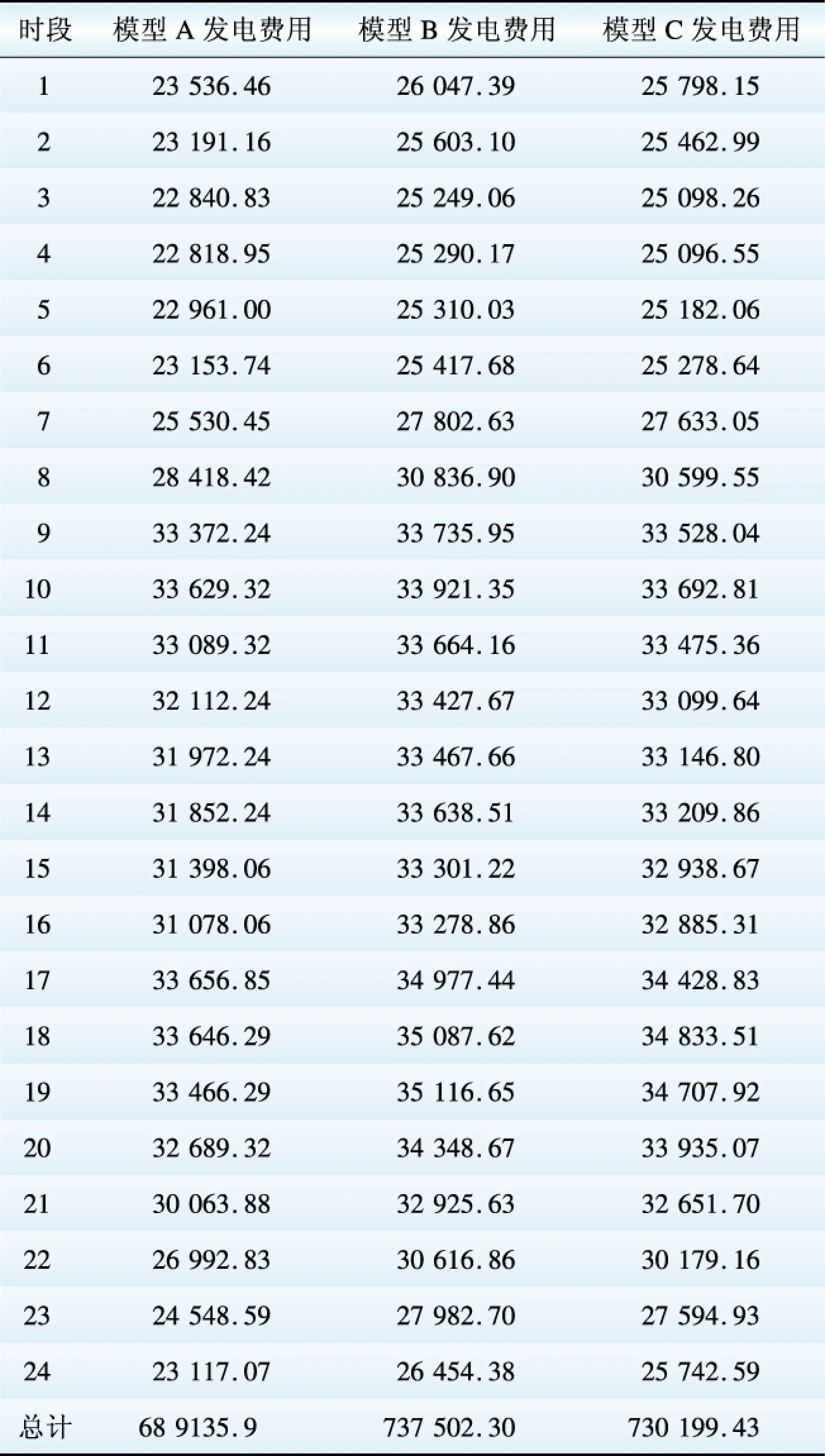
3种模型的经济性对比如表4所示，对比可知，模型B和模型C总成本为737 502.30$和730 199.43$，而模型A的总成本偏小为698 135.90 $，这是由于模型B和模型C需要调节机组出力，使系统具有应对风电实际出力的调节能力，但是增加了运行成本。相比较而言，模型C的成本略低于模型B的成本。模型C在调节机组出力时无需考虑风电出力均值，其相对于模型B具有更好的调节能力，从而使机组可以更接近经济运行点运行。

表4 24时段发电费用

Table 4 Power generation cost of 24-hour time period $

4.5 调节量分析

图5 模型B和模型C机组调节量对比Fig.5 Comparison of generator regulation between model B and model C

4.6 计算复杂度对比

由于模型B、模型C需要满足多种风电出力场景，因此其约束较多。从目标函数看，模型A含有分段函数，模型B含绝对值函数，模型C为常规的二次连续函数。因此，总体而言，模型A的计算量较为小，模型C次之，模型B的计算量最大。3种模型的计算量对比如表5所示。其中变量数目等于12台机组在24时段的机组出力、风电出力以及22个场景的调节量之和。约束数目即为所有变量的约束数目之和。仿真设备采用主频为3.00 GHz，4核处理器，内存为8GB，64位操作系统。

表5 3种模型的计算复杂度对比

Table 5 Comparison of computational complexity in three models

5 结 论

(1)模型C能够有效应对风电并网的随机特性，其面对不同风电场景时具有很强的鲁棒性，相对于模型B，其对机组的调节能力更强，从而保证系统能够面对不同的风电场景。

(2)通过对3种模型的对比，模型B与模型C的调节能力相当，但是，模型C具有更好的经济性，并且具有更快的计算速度。总体而言，与模型A和模型B相比，模型C在鲁棒性、经济性、计算速度等方面更具优越性。

[1]黎静华，桑川川.能源综合系统优化规划与运行框架[J].电力建设，2015，36(8)：41-48. LI Jinghua，SANG Chuanchuan.Discussion on optimal planning and operation framework for integrated energy system[J].Electric Power Construction，2015，36(8)：41-48.

[2]杨佳俊，雷宇，龙淼，等.考虑风电和负荷不确定性的机组组合研究[J].电力系统保护与控制，2014，42(3)：63-70. YANG Jiajun，LEI Yu，LONG Miao，et al.Study of unit commitment considering the uncertainty of wind farm and load[J].Power System Protection and Control，2014，42(3)：63-70.

[3]张步涵，邵剑，吴小珊，等.基于场景树和机会约束规划的含风电场电力系统机组组合[J].电力系统保护与控制，2013，41(1)：127-135. ZHANG Buhan，SHAO Jian，WU Xiaoshan，et al.Unit commitment with wind farms using scenario tree and chance-constrained programming [J].Power System Protection and Control，2013，41(1)：127-135.

[4]于佳，任建文，周明.基于机会约束规划的风-蓄联合动态经济调度[J].电网技术，2013，37(8)：2116-2122. YU Jia，REN Jianwen，ZHOU Ming.A chance-constrained programming based dynamic economic dispatch of wind farm and pumped-storage power station[J].Power System Technology，2013，37(8)：2116-2122.

[5]LI J H，WEN J Y，CHENG S J，et al.Minimum energy storage for power system with high wind power penetration using p-efficient point theory [J].Science China Information Sciences，2014，57(12)：2475-2486.

[6]LIU X，XU W.Economic load dispatch constrained by wind power availability：A here-and-now approach[J].IEEE Transactions on Sustainable Energy，2010，1(1)：2-9.

[7]WANG Q，WANG J，GUAN Y.Wind power bidding based on chance-constrained optimization[C]//IEEE Power and Energy Society General Meeting.San Diego：IEEE,2011：1-2.

[8]LIU X.Economic load dispatch constrained by wind power availability：A wait-and-see approach[J].IEEE Transactions on Smart Grid，2010，1(3)：347-355.

[9]徐秋实，邓长虹，赵维兴，等.含风电电力系统的多场景鲁棒调度方法[J].电网技术，2014，38(3)：653-661. XU Qiushi，DENG Changhong，ZHAO Weixing，et al.A multi-scenario robust dispatch method for power grid integrated with wind farms[J].Power System Technology，2014，38(3)：653-661.

[10]黎静华，韦化，莫东.含风电场最优潮流的Wait-and-See 模型与最优渐近场景分析[J].中国电机工程学报，2012，32(22)：15-23. LI Jinghua，WEI Hua，MO Dong.A symptotically optimal scenario analysis and wait-and-see model for optimal power flow with wind power[J].Proceedings of the CSEE，2012，32(22)：15-23.

[11]谢敏，闫圆圆，刘明波，等.含随机风电的大规模多目标机组组合问题的向量序优化方法[J].电网技术，2015，39(1)：215-222. XIE Ming，YAN Yuanyuan，LIU Mingbo，et al.A vector ordinal optimization method for large-scale multi-objective unit commitment considering stochastic wind power generation[J].Power System Technology，2015，39(1)：215-222.

[12]李嘉，何光宇，刘锋，等.考虑风电出力不确定性与半绝对离差风险的机组组合模型[J].电力建设，2014，35(12)：46-53. LI Jia，HE Guangyu，LIU Feng，et al.Unit commitment model considering uncertain wind power and lower semi-absolute deviation risk [J].Electric Power Construction，2014，35(12)：46-53.

[13]黎静华，文劲宇，程时杰，等.考虑多风电场出力Copula 相关关系的场景生成方法[J].中国电机工程学报，2013，33(16)：30-36. LI Jinghua，WEN Jinyu，CHENG Shijie，et al.A scene generation method considering copula correlation relationship of multi-wind farms power[J].Proceedings of the CSEE，2013，33(16)：30-36.

[14]SURENDER REDDY S，BIJWE P R，ABHYANKAR A R.Real-time economic dispatch considering renewable power generation variability and uncertainty over scheduling period[J].Systems Journal IEEE, 2015,9(4): 1440-1451.

[15]董晓天，严正，冯冬涵，等.计及风电出力惩罚成本的电力系统经济调度[J].电网技术，2012，36(8)：76-80. DONG Xiaotian，YAN Zheng，FENG Donghan，et al.Power system economic dispatch considering penalty cost of wind farm output[J].Power System Technology，2012，36(8)：76-80.

[17]翁振星，石立宝，徐政，等.计及风电成本的电力系统动态经济调度[J].中国电机工程学报，2014，34(4)：514-523. WENG Zhenxing，SHI Libao，XU Zheng，et al.Power system dynamic economic dispatch incorporating wind power cost[J].Proceedings of the CSEE，2014，34(4)：514-523.

[18]JABR R，PAL B C.Intermittent wind generation in optimal power flow dispatching[J].Generation，Transmission & Distribution，IET，2009，3(1)：66-74.

[19]ZHANG S，SONG Y，HU Z，et al.Robust optimization method based on scenario analysis for unit commitment considering wind uncertainties[C]//IEEE Power and Energy Society General Meeting.San Diego：IEEE，2011：1-7.

[20]WANG J，SHAHIDEHPOUR M，LI Z.Security-constrained unit commitment with volatile wind power generation[J].IEEE Transactions on Power Systems，2008，23(3)：1319-1327.

[21]高红均，刘俊勇，刘继春，等.基于坏场景集的含风电机组组合模型[J].电力系统保护与控制，2013，41(10)：27-32. GAO Hongjun，LIU Junyong，LIU Jichun，et al.The unit commitment with wind power based on the bad scenario set[J].Power System Protection and Control，2013，41(10)：27-32.

[22]张晓辉，闫柯柯，卢志刚，等.基于场景概率的含风电系统多目标低碳经济调度[J].电网技术，2014，38(7): 1835-1841. ZHANG Xiaohui，YAN Keke，LU Zhigang，et al.Scenario probability based multi-objective optimized low-carbon economic dispatching for power grid integrated with wind farms[J].Power System Technology，2014，38(7)：1835-1841.

[23]LI Jinghua，FANG Jiakun，WEN Jinyu，et al.Optimal trade-off between regulation and wind curtailment in the economic dispatch problem[J].CSEE Journal of Power and Energy Systems.2015，1(4)：37-45.

[24]LI Jinghua，LAN Fei， WEI Hua.A scenario optimal reduction method for wind power time series [J].IEEE Transactions on Power Systems, 2016, 31(2)：1657-1658.

(编辑 蒋毅恒)

Comparative Analysis of Wait-and-See Model for Economic Dispatch of Wind Power System

LI Jinhua1, ZHU Dunlin1, PAN Yi2

(1.Guangxi Key Laboratory of Power System Optimization and Energy Technology (Guangxi University)，Nanning 530004， China；2. China Electric Power Research Institute, Beijing 100192， China)

To make a better choice of the model of the power system dispatching plan with the random characteristics of wind power, this paper compares three economic dispatch wait-and-see models based on wind power scenario. The difference between two kinds of objective functions are compared and analyzed, which are ‘the minimum distance to the mean of wind power’ and ‘the minimum adjustment amount of dispatching plan’. Based on the power balance equation, we deduce and compare the dispatching plans obtained by three models and the regulation ability and adjustment amount for coping with the actual possibility of wind farm scenarios. Finally, taking the IEEE 24 node system as the example, we compare and analyze the simulation results of three models from the aspects of operating cost, adjusting ability, adjusting range, abandoning air volume, and so on. The analysis results show that the model with the minimum adjustment as objective has obvious advantages in robustness, economy and computation speed compared with other two models. The proposed three economic dispatch models and the comparative analysis results can provide important references for the dispatching plan optimization of the wind power system scheduling schemes.

wait-and-see model; economic dispatch; dispatching plan; wind power scenario; random characteristics

国家自然科学基金项目(51377027)；国家电网公司科技项目(DZ71-14-001)；广西大学研究生教育创新计划项目(YCSZ2015053)

TM 61

A

1000-7229(2016)06-0062-08

10.3969/j.issn.1000-7229.2016.06.010

2016-02-19

黎静华(1982)，女，教授，博士生导师，主要从事电力系统优化运行与控制，大规模风电并网等方面的研究工作；

朱敦麟(1991)，男，硕士研究生，主要从事电力系统优化运行与控制等方面的研究工作；

潘毅(1968)，女，博士，主要从事系统运行调度等方面的研究工作。

Project supported by National Natural Science Foundation of China(51377027 )