关注图形特征 积累思维经验
——以“长方形和正方形的周长”教学为例
2016-02-15陈芬芬
□陈芬芬
关注图形特征 积累思维经验
——以“长方形和正方形的周长”教学为例
□陈芬芬
思维经验是一种在思维活动中获得的过程性体验,其核心是如何思考的经验。教学中,教师要让学生在感悟和体验中开展思维活动,经历思维的全过程。“长方形和正方形的周长”一课的教学,试从研究图形的特征入手展开周长教学,通过不断比较、层层剥离,使学生最终体会到特殊的外在形式会有特殊的思维方式,从而积累数学思维经验。
图形特征 思维经验 长方形和正方形的周长
数学教学既要让学生掌握一定的知识技能,同时也要让学生在特定的数学学习活动中发展思维,积累活动经验。而数学活动经验的积累主要包括“实践活动经验”的积累和“思维活动经验”的积累。相对于“实践经验”,“思维经验”更为抽象、更为隐性,其核心是如何思考的经验,它是一种在思维活动中获得的过程性体验。因此,在教学中,我们要让学生在感悟和体验中经历思维的全过程,充分挖掘思维的本源,开展思维活动,展开思维过程,从而积累数学思维经验。以下是笔者以“长方形和正方形的周长”一课为例来谈如何积累数学思维经验的粗浅思考。
“长方形和正方形的周长”是在学习了长方形和正方形的特征及周长的意义的基础上学习的内容,其教学目标是让学生理解和掌握长方形和正方形周长的计算方法。如果说,单从学会计算的角度来考虑,单纯的套用公式学生易懂、教师易教。但如此一来,整个教学活动没有学生思维的介入,缺乏思考性,学生也就无法获得思维的过程性体验。因此,本课试着从研究图形的特征入手展开周长教学,使学生最终体会到特殊的外在形式会有特殊的思维方式,从而积累数学思维经验。
一、在描绘中挖掘本源
教学中,教师要考虑学生思维的源头,也就是让学生感受解决问题的最初想法。通过比一比、说一说等形式寻求思维的起点,理清思维的脉络。
【环节1】
课始,师出示三幅图:
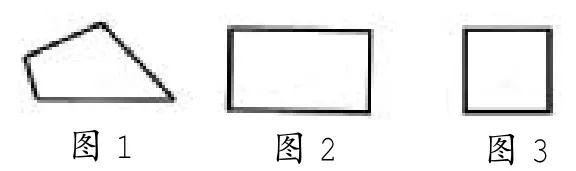
师:这三幅图形的周长在哪儿?你能比画一下吗?
生1:图1的周长是从这里开始,沿着它所有边绕一圈,然后再回到这里。(边说边用手沿着图形比画了图形所有的边)
生2:……
生3:……
生2和生3用同样的方法描绘了图2、图3这两幅图的周长。
【思考】
在此环节中,学生的思维起点是什么?不言而喻,应该是“周长的意义”。学生在用手比画周长、用语言描绘周长之前必须思考的是“什么是周长”。只有当学生明白了“封闭图形一周的长度就是它的周长”后,才能较好地解决“周长在哪里”的问题。因此,要想较好地解决这个问题,就必须充分挖掘学生思维的本源,弄清学生的真实思维过程,通过对图形周长的描绘,较好地解决“周长在哪里”的问题。
二、在比较中寻求突破
教学中,每个学生的思维方式都不同,因此,我们要尽可能地倾听每个学生的思考过程,让他们的思维介入教学活动,并在比较中寻求新的突破,只有这样学生才能得到思维的过程性体验。
在探究如何测量周长的过程中,学生的思维是活跃的,他们在对周长意义的理解中,感受求周长的多种方法。而在此过程中,教师的任务只是引领,通过“你量了几条边”“你是怎么算的”两个问题,唤起学生的思维。
【环节2】
师:(继续利用三幅图)你能试着求出这几幅图的周长吗?请你量一量、算一算。
反馈一:图1的反馈结果
生:图1,我量了4条边,只要把4条边的长度相加就是它的周长了。
反馈二:图2的反馈结果
生:图2,我也量了4条边,把4条边的长度相加就是它的周长了。
生:图2,只要量两条边就可以了。用长边×2+短边×2就可以算出它的周长了。
师追问:为什么只量两条就可以了?
生:图2是一个长方形,长方形的对边相等。
生:我也量两条边,我先求长边加短边的和,再乘2。
反馈三:图3的反馈结果
生:图3,我量了1条边,把每条边的长度相加就可以了。
生:图3,我也量了1条边,但我只要用1条边的长度×4就可以了。
师追问:为什么都只量1条边,可算法却不一样呢?
生:图3是一个正方形,每条边的长度都相等,所以用1条边的长度×4更简便。
【思考】
不同的答案,分别代表不同的思维层次,但学生解决问题的最初想法是一样的:“什么是周长”“如何求周长”,周长就是把一个封闭图形中所有边的长度相加。但细细考虑,为什么学生会有不同的量法、不同的算法,除了学生思维的角度、深度不同外,还有其他不同吗?在教师不断的追问中,我们得到了答案:图2是长方形,对边相等,只要量一条长和一条宽就可以了;图3是正方形,每条边都相等,只要量一条边就可以了;而图1是个普通四边形,每条边的长度都不相等,所以要量四条边。原来,不同的图形,求周长的方法可以不同;相同的图形,求周长的方法也可以不同,这其中的关键在于图形的特征不同。通过不断地比较、层层地剥离,使学生对求周长的方法有了更清晰的认识,也使学生的数学认知和思维水平都得到了突破。
三、在反思中明确方向
通过比较,能使学生的数学思维介入教学活动,从而获得更充分的过程性体验。而通过反思,使内隐的思维经验外显化,使学生的数学学习有了明确的方向。
【环节3】
师:刚才我们用各种不同方法求出了三个图形的周长,你觉得有什么相同或不同的地方吗?(同桌交流)
生:都可以用四条边相加来求周长。
生:算法不一样。
师追问:为什么?
生:这三个图形边的特征不一样。
师小结:原来是和边有关系,边的特征不一样,求周长的算法也有所区别。
【思考】
通过总结反思,将解决问题的矛头指向“边”的特征,正是因为图形中边的特征不同,才使求周长的方法有了不同。这看似简单的环节,却是十分必要的,因为只有在不断的思辨中,学生的思维能力才能进一步发展,思维经验才能得到积累。
四、在迁移中建立模型
思维经验的积累不是一蹴而就的,而是一个不断深化、逐步提升的过程。有时,思维经验更是在对解决相关数学问题的举一反三、触类旁通中,通过对原有知识经验的迁移,形成结构化的数学模型,使学生的数学思维走向深刻。教学中,教师可引导学生多用“分类、比较”等方法,以此想通、悟透知识间的来龙去脉,从而积淀思维经验,发展思维能力。
【环节4】
在结束新知教学后,拓展部分有这样一个环节:出示题目“寻找差不多”(如下图)。

师:要想求出上面图形的周长要量几条边呢?为什么?可以怎么算?
生:图4,只要量1条边,因为每条边的长度是相等的。只要量1条边的长度再乘3就可以了。
生:图5,量1条边,再乘5。
生:图6,量2条边,一条长边一条短边,用长边加短边的和乘2就可以了,因为有这样的两组!
生:图9,量2条边,一条长边一条短边,但要乘4,因为有这样的四组!
师:这些图形中,哪些和正方形的周长计算差不多?哪些和长方形的周长计算差不多?为什么?
生:图4、图5、图7和正方形的周长计算差不多;图6、图8、图9和长方形的周长计算差不多!
生:图4、图5、图7和正方形差不多,每条边的长度都相等;图6、图8、图9和长方形差不多,分别有一条长边和一条短边。
师小结:同学们不仅学会了求长方形和正方形的周长,还学会了用同样的方法求类似图形的周长。
【思考】
这个环节,看似简单,实则是学生思维真正积极投入、参与数学活动的过程。当学生在教师的引导下思考“要量几条边、可以怎么算”的时候,其实正是他们在找寻这些图形最基本的特征。如,图4为什么只量1条边,但要乘3;图9为什么要量2条边,但要用两边之和乘4。通过深入的观察,我们发现,原来这些图形和长方形、正方形一样,它们的边都有各自不同的特征,因而在计算周长时会有不同的量法和算法。而当教师问及“哪些和正方形的周长计算差不多?哪些和长方形的周长计算差不多?”时,更是激发了学生的深度思考,于是将这些特殊的图形根据边的不同进行分类,并与长方形、正方形进行比较,找出它们之间共同的特征,进而将长方形、正方形的周长计算迁移到这一类图形周长的计算,建立起“如何求周长”的数学模型。在此过程中,学生的数学思维一直处于积极的体验过程中,通过不断的比较,深化学生的数学认知,提升数学思维水平。
五、在拓展中提升品质
思维经验的积累还需进一步拓展思维空间、提升思维品质。如果说,让学生在不断地感悟和体验中解决“如何求周长”的问题,使学生的数学思维得到较好的发展。那么,“求彩带有多长”一题的出示(如下图),又将学生思维的发展从二维过渡到了三维。
【环节5】

出示题目:
师:要求彩带有多长,其实就是算哪几条边的长度呢?可以怎么算?
生:两条2分米、两条1分米。(学生拿着实物盒子边比画边说)
生:2×2+1×2=6(分米)。
师:你能想象其实就是求哪个图形的周长吗?你有什么好办法让大家看得更清楚在哪个面吗?
生:我把这条带子慢慢地移出来,其实就是求这个长方形的周长了。(学生边说边移动彩带到最边上,让学生明白求彩带的长度就是盒子中其中一个面的周长)
【思考】
彩带所围成的图形是个长方形,但它处于一个三维的空间中,需要借助想象才能完成。而此时,教师顺势引导“你有什么好办法让大家看得更清楚吗”,让学生明白可以通过平移让彩带变得直观,也将学生的认知从三维拉回到二维平面图形上。通过这样的拓展,发展了学生的思维空间,提升了思维品质,积累了思维经验。当然,这种思维经验的积累还将为后续“棱长总和”的学习打下基础。
经验的生成离不开数学活动,而伴随着思维的参与,经验才会具有创造性的生长。思维经验是学生在积极参与数学活动中获得的一种过程性体验,体验越丰富,经验就积累得越多。只要教师能让学生在各种活动中不断感悟、不断积淀各种思维经验,必将促进学生思维能力的发展。
[1]郭玉峰.数学活动经验研究——理论与实践探讨[D].东北师范大学博士论文,2012.
[2]沈华斌,范新林.连通思考节点 积淀思维经验[J].中小学数学,2015.
(浙江省湖州市月河小学教育集团 313000)
