“用几何板算面积”学习活动设计设计

□ 设计 郑 倩 指导 郜舒竹

“用几何板算面积”学习活动设计设计

□ 设计 郑 倩 指导 郜舒竹

“变教为学”提倡以学为主的学生活动，教学内容要激发学生动机，凸显学生的学习活动。学科实践活动课程的开展离不开“变教为学”式的课堂。学生活动的内容与开展方式成为了优质课堂的重要组成部分。以“用几何板算面积”为例，对教学内容进行改进与设计，形成能够适用于小学综合实践活动及数学实践活动课堂中的活动设计，使学生在学习活动中获得更多的知识与能力，并为一线教师开展数学实践活动提供资源。

变教为学 学科实践活动课程 学生活动

“变教为学”的理念提倡把课堂上以教师“讲授”为主的教学活动，改变为学生自主或合作开展的“学习”活动，让学生的学习活动占据主导地位并且贯穿始终。教师应聚焦于“学什么”以及学生“怎样学”。[1]

学科实践活动课程的提出，意味着教师应为学生设计适合学生研究探索的学科实践活动。而现阶段，教师设计的学生活动缺少内容、方法和过程。教师没有上课的素材，也很难在教材中发现适合学生活动的内容。无论是在学科教学中，还是在综合实践课程以及学科实践活动课程中，教师都应该为学生设计有效的学习活动，但是教师的最大困难就在于备课中为学生设计什么活动。因此，本文以“用几何板算面积”为例进行探究活动设计，可以用于诸如“综合与实践”或“学科实践活动课程”的教学。

“用几何板算面积”这一探究活动是通过让学生自己制作一个几何板来探究一些简单图形的面积。几何板是帮助学生探究几何图形周长和表面积的学具。几何板的实际意义就是将经常使用的网格图立体化，让学生由二维平面中的描画转变为三维空间中的操作。

本活动可以与人教版三年级下册“认识面积”一课结合开展。在“认识面积”一课中，学生理解把正方形作为“单位1”，并能将图案画在方格纸上，通过数正方形个数的方法得出图形的面积。在“用几何板算面积”这一活动中，学生不但能够更深刻地理解方格纸在几何板上的体现，还可以用自己制作的几何板学具解决面积问题，几何板的好处在于可以让学生变换多个图案进行探索，每变换一个图形都非常方便。活动中，深化了学生探索图形面积的方法，使学生巩固了面积这一概念，增强了课程的趣味性，也为今后学习简单图形面积公式打下了基础。

本活动基于“明确问题，产生动机”“过程方法，获得结论”“多样比较，错误辨析”“关联应用，总结提升”四个层次[2]，对本探究活动进行设计，活动分为“问题与动机”“过程与设计”“实施与操作”“结果与评估”“关联与应用”“总结与反思”六个步骤。具体内容如下：

一、问题与动机

教师引导学生对以往的知识进行回顾与思考，并向学生提问：我们已经认识了许多平面图形，平面图形的大小就是它们的面积。你能回忆出哪些平面图形呢？你又能用什么办法来算出它们的面积呢？

学生回忆已学的平面图形：长方形、正方形、平行四边形、三角形、圆。在思考它们的面积时，学生会出现不同的关注点：有些学生可能会随便说出一些数字，有些学生可能会给出一些估算方式，如将所求图形与已知面积的图形相比较，若比已知图形大，则所求图形面积比已知图形大；反之，若所求图形比已知图形小，则面积比已知图形小。学生可以通过教师的提问充分思考与本活动有关的知识，这对后续活动的开展具有非常重要的引领作用。

二、过程与设计

需要的材料有：硬纸板、大头针、橡皮筋、铅笔、尺子。

教师首先让学生以四人为小组观察几何板的特点，了解其工作原理。再观察为学生准备的学具，思考材料中的每一件用具的用途。

老师这里有一个几何板，你能观察它的构造并猜猜它的工作原理吗？说说它有什么特点，每个同学面前都有一份制作材料，你能通过观察与对比想明白这些材料分别起到了什么作用吗？教师首先让学生通过观察来了解几何板，学生可以充分思考其原理，锻炼学生的观察能力。在制作前先思考各材料的用途，能够促进学生对活动的理解，增强学生的思维能力。

几何板是由1块硬纸板和36根大头针制成的。横竖每相邻两根大头针之间的距离是相等的。我们可以用橡皮筋围成要求的图案，再看一看它是由几个小正方形组成的，如果有半个正方形的情况，可以用拼凑的方法数一数，得出面积。在硬纸板上按等距离打格是为了保证每个小正方形的面积是相同的，即制作“单位正方形”。在每条线的交点处插上大头针，大头针起到支撑橡皮筋的作用，将橡皮筋围在大头针上就可以围出想要的图形。

三、实施与操作

需要的材料有：硬纸板、大头针、橡皮筋、铅笔、尺子。

教师引导学生对几何板进行制作。同学们已经检查了材料，并且了解了制作几何板的方法，下面请同学们亲自动手做一做几何板。学生按步骤制作几何板，能够提升其动手能力，并在动手的过程中不断思考。

学生按照规定尺寸测量并在硬纸板上描点画线，在每条线的交叉处插入大头针，如图 1所示。

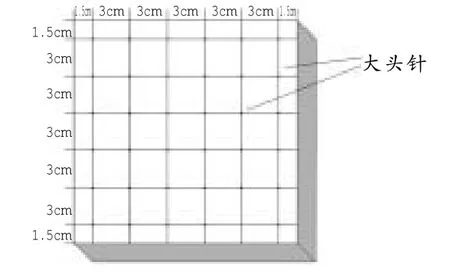
图1 几何板制作图示

学生在插入大头针时应注意安全，小心不要伤到手指。

学生在理解原理的情况下进行制作，使学生的制作过程更加有条理，并增强了学生的动手操作能力。

四、结果与评估

教师引导学生对一些问题进行讨论。制作完几何板后，我们就要使用它来解决问题。请同学们用橡皮筋围出和老师相同的图案，如图 2所示。学生在制作几何板后再对问题进行解决，这样更加有助于学生进行思考。

图2 教师出示图案

我们把几何板中的每一个小正方形的面积看作1，请你回答以下问题，并将答案填在记录单上。

1.所围图形中最小的正方形面积是______。

2.所围图形中第二小的正方形面积是______。

3.所围图形中第三小的正方形面积是______。

4.所围图形中最大的正方形面积是______。

5.所围图形中最小的三角形面积是______。

6.所围图形中最大的三角形面积是______。

学生先用橡皮筋围出教师所出示的图形。通过回答一系列的问题，逐渐体会几何板的用法以及数格子的方法。学生需要找到7种不同大小、不同形状的图形，分别判断其面积，在判断三角形的面积时需要对半格进行拼接与割补。

最小的正方形由4个“半格”组成，因此它的面积为2。

第二小的正方形由4个“整格”组成，因此它的面积为4。

第三小的正方形由4个“整格”和8个“半格”组成，因此它的面积为8。

最大的正方形由16个“整格”组成，因此它的面积为16。

最小的三角形由1个“半格”组成，因此它的面积为0.5。

最大的三角形由2个“整格”和4个“半格”组成，因此它的面积为4。

五、关联与应用

教师鼓励学生进行创作。“同学们在完成了老师布置的任务后，想不想自己围一围喜欢的图形呢？请大家在几何板上创作自己的图案，并算一算它的面积，将数据写在记录单上。”学生发挥创造力，同时能够对几何板算面积的方法进行巩固。

学生自己创造喜欢的图形，发挥主观能动性。面对复杂图形，学生可将复杂图形拆分成简单的基本图形，从而算出面积。

六、总结与反思

教师引导学生对活动进行总结。“经历了制作几何板以及用几何板计算面积的活动，你有什么收获？你从中学习到了什么道理？在这个活动中，你遇到了什么困难？又有哪些吸引你的地方？”

在这个活动中，学生制作了几何板，并能够运用单位正方形来计算简单图形的面积。单位正方形的面积可看为1，那么所围图形的单位正方形个数就是几何图形的面积。在数格子时，用到了割补的方法，将半格与半格拼在一起看作1。用几何板算面积可以在不使用面积公式的情况下算出图形的面积。理解其中的原理是本活动比较困难的地方。创造多样的图案是本活动有趣之处。学生在制作几何板时可能会在扎大头针时遇到困难，导致几何板出现不牢固的情况。

在“用几何板算面积”这一活动中，学生能够体会将方格纸立体化，也让学生深化了探索图形面积的方法，使学生巩固了面积这一概念，增强了课程的趣味性，也为今后学习简单图形面积公式打下了基础。本活动以数学知识为基础，让学生通过自主探究、动手操作来获得各方面的提升，不但在数学学科方面有所增强，同时也增强了学生的观察能力、动手能力、创造能力等。这样的课堂是“以学为主”的课堂，实现了“变教为学”的课堂。

[1]郜舒竹.小学数学这样教[M].上海:华东师范大学出版社，2015.

[2]郜舒竹.“变教为学”需要螺旋上升的学习活动[J].教学月刊·小学版（数学），2015（10）.

（首都师范大学初等教育学院 100048）

说明：本刊上期刊登的《中美数学教学的异与同（一）——国际数学教育专家黄荣金博士访谈录》一文中黄荣金博士应系美国中田纳西州立大学数学系副教授，特此说明。