数形结合在中学数学中的应用
2016-02-15周子晴长沙市南雅中学湖南长沙410000
周子晴(长沙市南雅中学,湖南长沙410000)
数形结合在中学数学中的应用
周子晴(长沙市南雅中学,湖南长沙410000)
在中学数学学习中,可以利用数形结合的思想将抽象的概念通过图形的方式形象化地展示出来,从而更清晰的学习数学概念。对此,本文首先对数形结合概念进行了分析,并对其在数学解题中的应用进行了详细探究。
中学数学;数形结合;应用方式
1 引言
数形结合是一种非常重要的学习思路,就是根据数和形之间一一对应的关系,把抽象的数学语言和数学关系与直观的、容易理解的几何图形和位置关系相互联系,将学习中遇到的数学难点具体化和简单化,通过应用数形结合法,能够有利于日常数学知识的学习。
2 数形结合概念
数形结合指的是根据数与形之间的对应关系,将数与形进行相互转化,以此解决数学学习中遇到的各种难点。通过应用数形结合思想,有利于我们掌握数学问题的条件和结论之间的关系,将其中的内在联系在图形或者数轴上表示,使之转化为求解几何或者代数问题,从而对难点进行细致分析,在具体的应用过程中,不仅需要详细了解代数的意义,而且还需要揭示出问题的几何意义,通过将数量关系和空间形式相结合,寻求解题思路。
3 数形结合在中学数学中的应用方式
3.1 数与代数的数形结合
在中学数学学习过程中,代数的学习是重点,也是难点,我们在解答代数问题时,如果仅仅应用代数解题方法,则在具体的解题过程中,需要处理比较复杂的假设等问题。对此,我们可以将抽象的代数与形象的函数图像相结合,并将代数以坐标、数轴的方式表现出来,这样便于我们更好的理解题目本身。通过应用坐标,能够处理很多内容,包括二元一次方程组、函数、平移变换、对称变换等等,在数轴上,可以将数与代数图形化,通过数形结合,简化数学难题。
3.2 “空间与图形”中的数形结合
在中学数学学习中,几何知识是十分重要的学习内容,在几何学习过程中,通过图形图像进行解题,更加直观。但是,我们在学习几何图形的空间变化时,往往很难理解几何图形的变化思路,对此,可以采用空间与图形相结合的办法,更加直观和深刻的了解几何知识,提高自己的空间思维能力。
3.3 “概率和统计”中的数形结合
在中学数学学习中,概率学习难度较大。概率的抽象性较强,因此,我们在理解概率或计算概率的过程中,如果仅仅根据题目中所给出的提示,一般需要耗费大量的思考时间,容易造成思维混乱,对此,我们可以根据题目中所给的提示信息,通过统计图表的方式展现出来,这样有利于我们对概率的整体情况进行分析判断,提高解题效率。
4 数形结合在中学数学解题中的应用实例
4.1 数形结合在抽象函数上的应用
将数形结合的方法合理灵活地运用有助于将数学问题形象化、具体化,在实际问题的解答过程中非常有效。
例题:如果一直f(x)为一个二次函数,且其在f(0)的时候取最小值。现已知f(a)<f(2),求a的取值范围是多少?
解题方法:如果直接进行借到的时候会发现难度比较大,但是如果可以根据已知条件画出如图1所示的几何示意图,则可以解决问题。由于f(x)为二次函数,且开口向上,那么a的取值一定是(-2,2)。
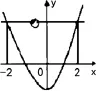
图1 f(0)为最小值的二次函数的示意图
4.2 利用数形结合思想讨论方程的根
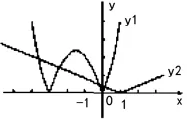
图2
有两组不同解x1,x2,
消y得x2+(3-a)x+a=0,故Δ=a2-10a+9>0,
且x1+x2=a-3<2,x1x2=a<1,联立可得0<a<1;
当4个交点横坐标有两个小于1,两个大于1时:
有两组不同解x3,x4,
消y得x2+(3-a)x+a=0,故Δ=a2-10a+9>0,
且x3+x4=a-3>2,x3x4=a>1,联立可得a>9,
综上,0<a<1或a>9。
4.3 利用图象解决函数问题
数是贯穿中学学习一条基本主线,中学数学的基础是平面直角坐标系和实数。
解题方法:分别画出函数y=3x+3的图象和反比例函数y=的图象,如图3所示,可以直接看出它们的交点所在的位置,即交点分别在第一象限和第三象限。
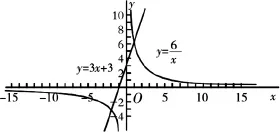
图3
5 结语
综上所述,数形结合思想在中学数学学习和解题过程中发挥着十分重要的作用,我们在日常解题过程中,可以将抽象的数学语言和直观的图形结合起来,将结合问问题代数化,将代数问题几何化,这样就能够便于我们对疑难问题进行透彻分析,并且掌握基本的数学概念和知识点,因此为了提高数学成绩,我们必须认真学习并熟练掌握数形结合思想的应用方式。
[1]陈建花,沈有建.初高中学生数学学习衔接存在的问题与对策[J].数学通报,2013,52(3):15~17.
[2]骆 丽.浅谈怎样学好初中代数[J].中学课程辅导:教学研究,2015,9(21):154~155.
G633.6
A
2095-2066(2016)36-0276-02
2016-11-12
周子晴(1999-),女,就读于长沙市南雅中学1407班。
