基于有限元分析的埋地电缆温升影响因素研究

茅大钧，肖 礼，刘国建

(1. 上海电力学院 自动化工程学院，上海 200090；2. 国家电网山东省电力公司 枣庄供电公司，山东 枣庄 277000)

基于有限元分析的埋地电缆温升影响因素研究

茅大钧1，肖 礼1，刘国建2

(1. 上海电力学院 自动化工程学院，上海 200090；2. 国家电网山东省电力公司 枣庄供电公司，山东 枣庄 277000)

针对YJLW02 66/110 kV 1*1000型电力电缆运行时，电缆载流量与电缆间距如何影响电缆发热的问题，研究IEC标准中关于电缆损耗的有关计算方法，以电缆导体损耗、绝缘介质损耗与金属护套损耗作为电缆内部发热源，利用有限元分析软件ANSYS建立单回路埋地电缆土壤直埋、排管2种敷设方式的模型，并进行仿真分析。结果表明：随着电缆载流量的升高，电缆导体温度会加速升高；随着电缆间距的增大，电缆导体温度逐渐降低，且当电缆间距大于0.2 m时，温度变化会趋于某个稳态值。

有限元分析；电缆温升；电缆载流量；电缆间距；电缆损耗

电缆通电自身会发热，其传输容量取决于电力电缆所能承受的最高温度，即在电缆绝缘层长期(例如30～50年)可靠运行的前提下，电缆导体的最高允许温度。如交联聚乙烯(XLPE)绝缘电缆，其最高允许温度为90 ℃；聚氯乙烯(PVC)绝缘电缆的最高允许温度为70 ℃[1]。当电缆运行温度超过这个温度时，虽然可能不会立即表现出故障态势，但无疑加速了电缆绝缘层材料的温升发热，进而加速绝缘层老化。长此以往，将容易导致电缆绝缘层过热击穿，造成电力事故。通过对电缆过热老化与寿命研究可知[2]：当交联聚乙烯电缆工作温度超过最高允许温度的7%时，电缆寿命将减少50%；当超过15%时，寿命将减少75%。

最大限度地利用电缆传输能力，避免传输线路的浪费，保证电缆长期运行于最高允许温度之下，并维持安全、可靠状态是电缆在运行中需要考虑的2个重要方面[2]。在密集与高负荷运行时，需要对电缆进行故障检测与维护，而对温度值的监测最能直接反应出电缆运行状态的健康与否。

目前，国内外针对各种电缆在线监测系统的研究众多，较为成熟的测温系统大致有红外测温仪、红外成像仪、感温电缆及热电阻式测温等，但是这些测温系统在运行过程中存在较多弊端，如只能进行局部测温，因此无法满足现代电力系统对于安全经济运行，高效稳靠检修的要求[3-4]。此外，对于电缆温度变量的在线监测，普遍存在着思维认识误区。电缆温度升高实则是一个渐变过程，当系统对实时温度进行监测达到预警值时，电缆内部可能早已发生过热现象，危及到电缆的安全稳定运行。因此，文中展开对电缆运行的发热机理研究，在达到系统阈值前就遏制电缆温升，使电缆在正常负荷时温升平稳，高峰负荷时安全运行。

笔者运用有限元分析软件ANSYS对可能影响电力电缆温升过高的多个因素进行仿真分析，并研究探讨其作用机理。

1 电缆损耗计算

应用有限元分析法对电缆温升进行研究时，首先应该确定电缆发热的热源[5]。由IEC 60287标准可知，电缆损耗主要有电缆导体损耗、绝缘介质损耗和金属护套损耗，将这3种损耗作为内部热源施加在有限元模型上用作相应热载荷分析。

1.1 电缆导体损耗

根据欧姆定律，电流Ic通过单位长度的导体所产生的损耗为

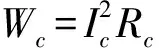
(1)

式中Rc为单位长度线芯的交流电阻，计算公式为

Rc=R0(1+Ys+Yp)。

(2)

式中R0为单位长度线芯的直流电阻；Ys为集肤效应系数；Yp为邻近效应系数。

对于圆形单芯或三芯电缆，Ys与Yp的计算公式分别为

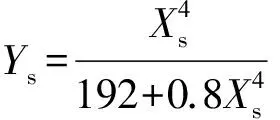
(3)

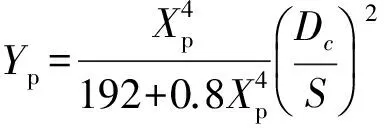
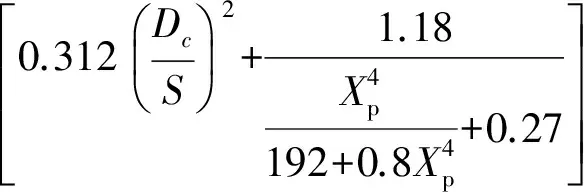
(4)

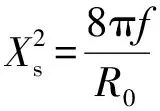
1.2 电缆绝缘介质损耗

单相电缆单位长度的介质损耗为

Wd=ωCU02tanδ。

(5)

式中ω=2πf；tanδ为介质损耗角正切，取0.004；U0为对地电压；C为单位长度电缆的电容，F/m，其计算公式为

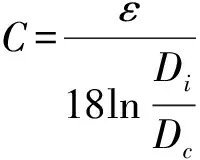
(6)

式中ε为绝缘材料的相对介电常数；PE取2.3，PVC取6.0；Di为绝缘层外径；Dc为线芯外径。

1.3 金属护套损耗

电缆金属护套是同心地套在导体周围的一层薄壁圆柱体[6]。导体回路产生的一部分磁通与金属护套相链，这部分磁通在金属护套中产生感应电动势，引起涡流损耗。为了防止感应电动势对电缆安全运行造成危害，常把金属护套两端接地，但这样便会构成电流回路，产生环流损耗[7-8]。所以金属护套中损耗主要包括环流损耗和涡流损耗：

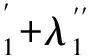
(7)

电缆金属护套的损耗与其接地方式有关。金属护套接地分为3种情况：金属护套两端接地、金属护套单点接地及交叉互联接地。每种特定情况均需考虑不同的损耗类型，即使对于同一种损耗在三角形排列敷设和水平排列敷设时的计算公式也不同。

2 埋地电力电缆有限元模型

笔者对一种埋地电力电缆YJLW02 66/110 kV 1*1 000(铜芯交联聚乙烯绝缘皱纹铝护套聚乙烯外护套)电缆(如图1所示)的横截面进行有限元模型构建。针对金属外护套两端接地、单端接地情况时，研究YJLW02 66/110 kV 1*1 000电缆在土壤直埋、管道内敷设2种方式下稳态温度场分布情况，并探讨影响电缆温度场分布的要素及其作用机理。

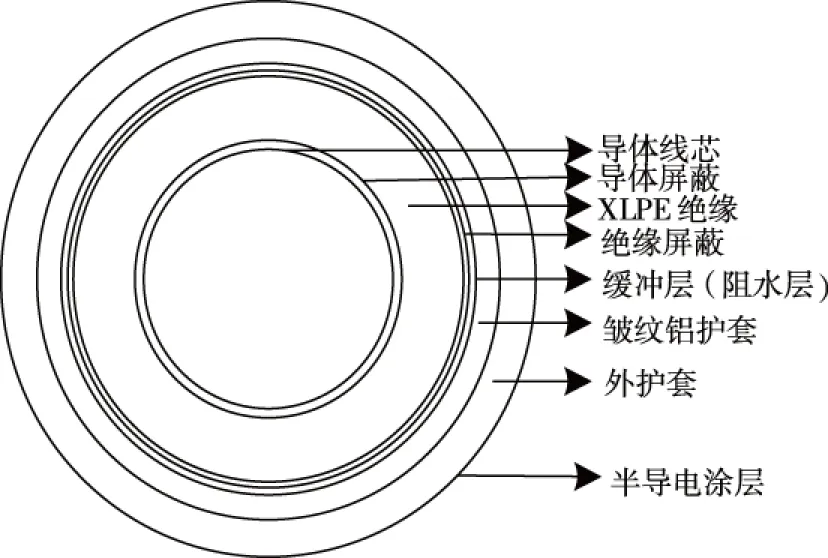
图1 YJLW02 66/110 kV 1*1 000电缆结构

在分析电力电缆温度场分布的过程中，做出如下基本假设[9]：

1)电缆内外传热达到相对热平衡后，随着时间变化，温度场是相对稳态的；

2)电力电缆近似为柱体，横截面看作同心圆；

3)导电芯导热性能良好，导体线芯的温度是均匀的；

4)各层护套之间没有空气等流体介入，为紧密接触结构，各护层之间以及线芯与各护层的接触电阻暂不予考虑。电缆的结构参数如表1所示。

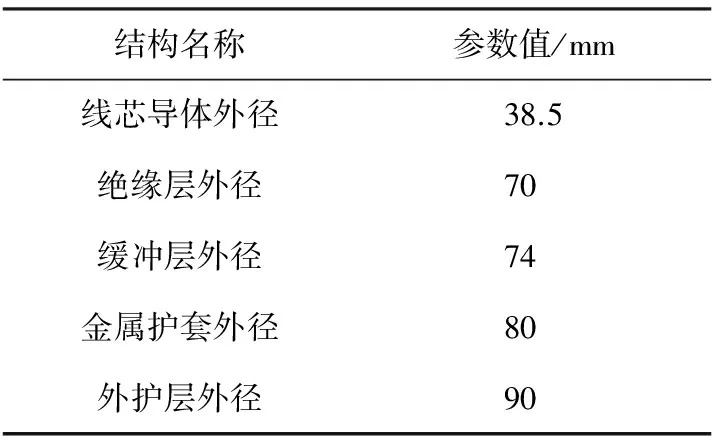
表1 电缆结构参数

基于ANSYS建立的土壤敷设单相电缆有限元模型及其网格划分模型，如图2所示。实际运行中，电缆三相同存在，依据不同的敷设方式[10]，建立如图3所示的有限元模型。

图2 电缆有限元ANSYS模型和有限元模型网格划分

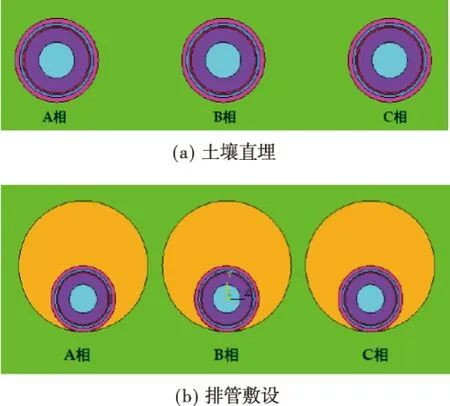
图3 土壤直埋和排管敷设电缆ANSYS模型

在电缆敷设的边界问题上，相关文献[11-12]表明：电缆周围1.2 m的土壤范围受电缆温度影响较大，超出该范围，土壤间热交换甚微，因此建立的空间模型上，电缆左、右两侧各余留2 m的土壤范围，电缆上层埋土距地表1 m，换热均匀频繁。

3 土壤直埋电缆仿真分析

3.1 不同电缆间距

电缆间距作用于线芯损耗时，主要影响邻近效应系数Yp。通过计算，不同电缆间距、邻近系数Yp、交流电阻及线芯损耗(通以低于1 000 A电流)关系如表2所示；线芯损耗随电缆间距变化曲线如图4所示。

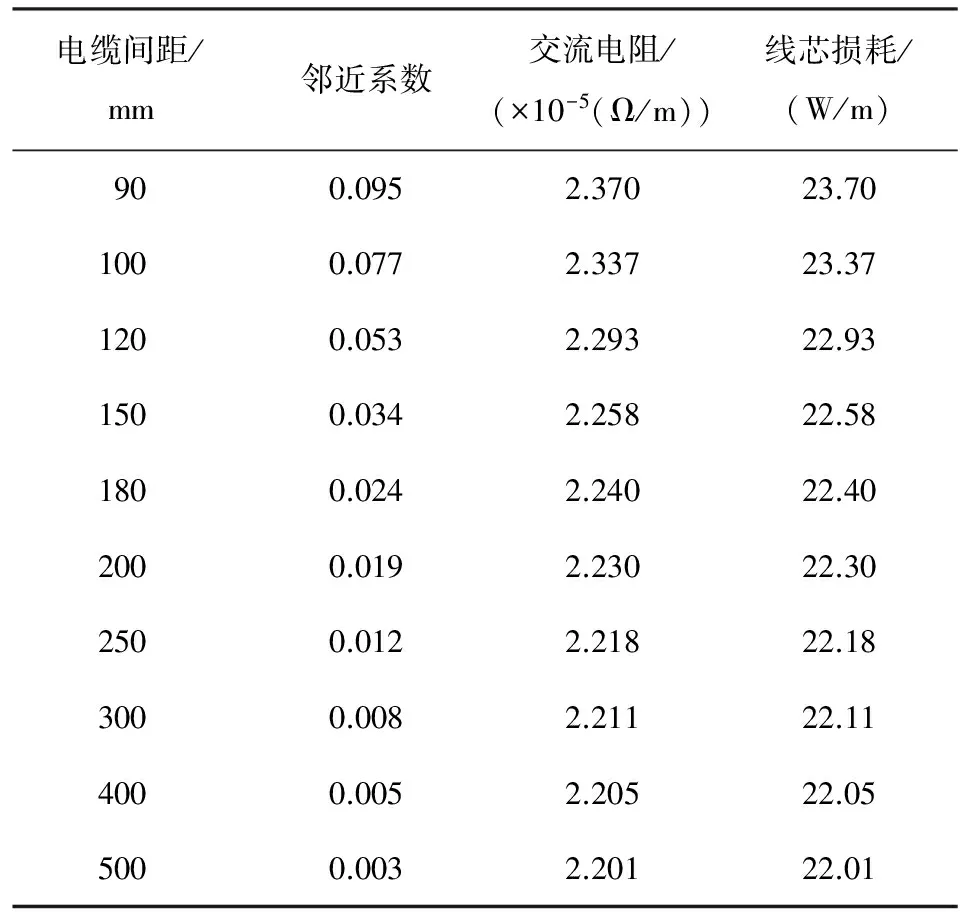
表2 电缆间距、邻近系数、交流电阻、线芯损耗数据对比

图4 线芯损耗随电缆间距变化曲线

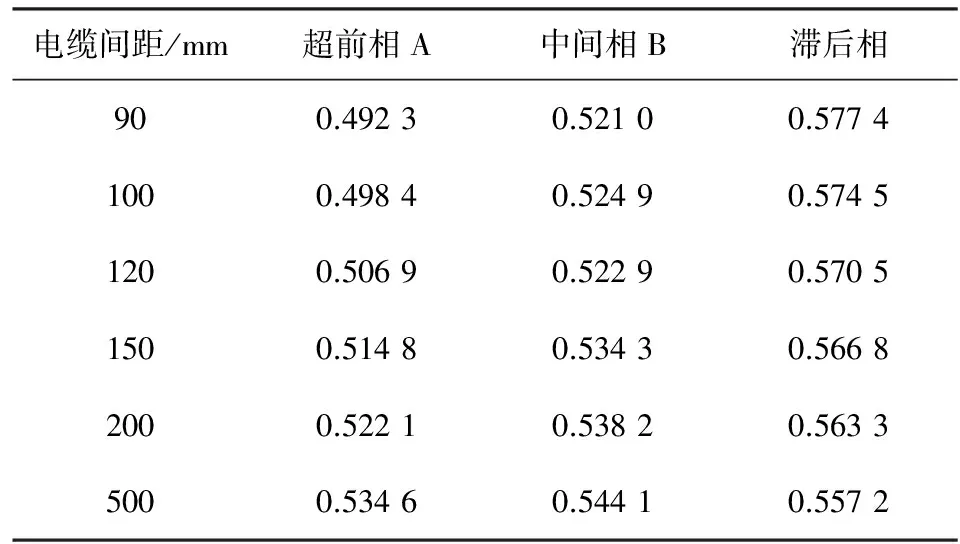
表3 缆护套环流损耗系数随电缆间距变化的数据对比

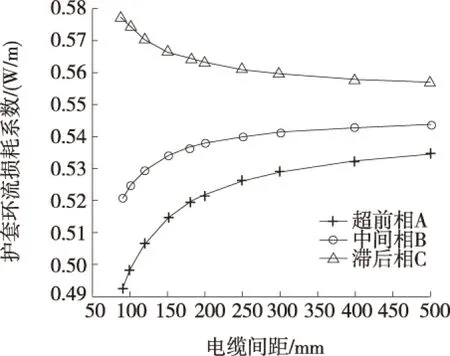
图5 护套环流损耗随电缆间距变化曲线

可以看出，电缆三相中，滞后相C的环流损耗最大，超前相A环流损耗最小；滞后相C的损耗随着电缆间距增大逐渐减小，另外两相反之，但最终趋于某固定值。

电缆的绝缘介质损耗只与电缆电流频率有关，与电缆间距无关。设定空气温度为40 ℃，地表与空气对流换热系数为12.5 W/(m2·℃)，深层土壤温度恒定20 ℃时进行ANSYS仿真分析。

由此，多次ANSYS仿真计算得到电缆间距与埋地电缆温度场分布如表4所示;电缆间距为300 mm时，埋地电缆温度场分布云图如图6所示；导体温度随电缆间距变化曲线如图7所示,可知随着电缆间距的增大，电缆导体温度逐渐降低，当电缆间距大于0.2 m时，导体温度趋于稳定。

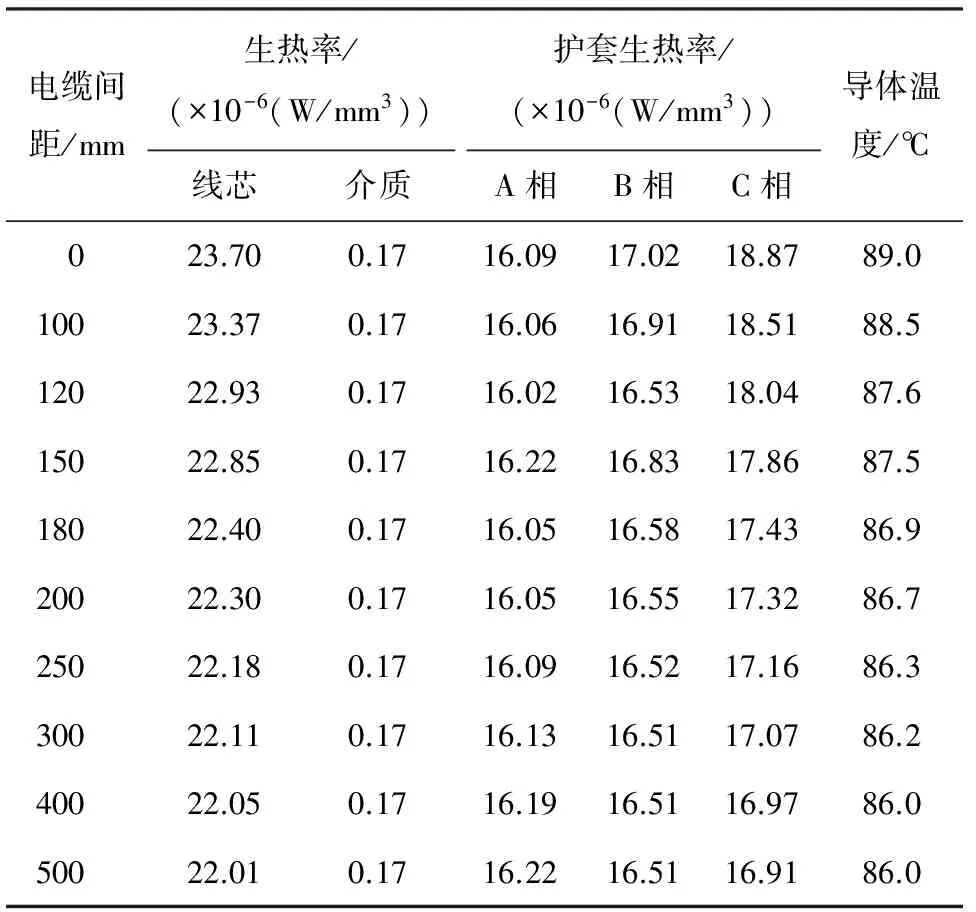
表4 电缆间距、生热率、导体温度数据对比

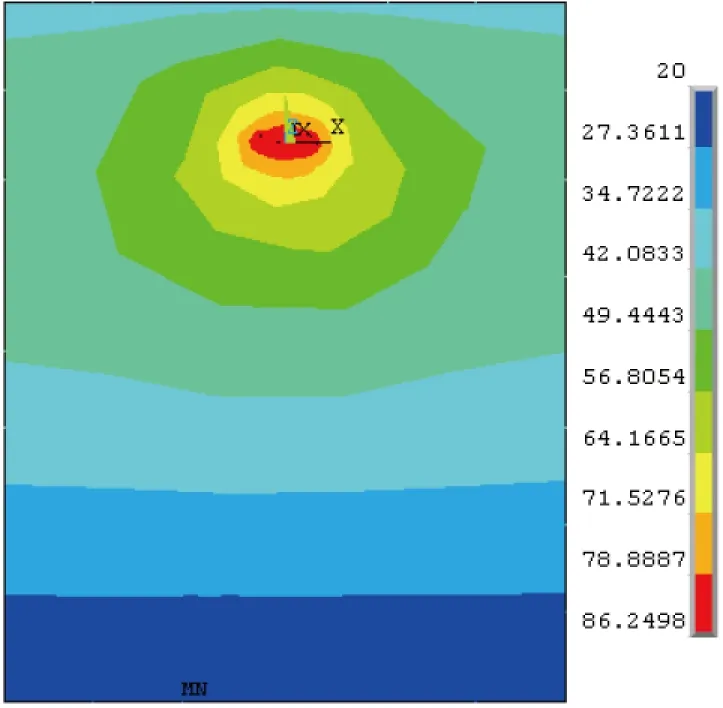
图6 间距为300 mm时，埋地电缆温度场分布云

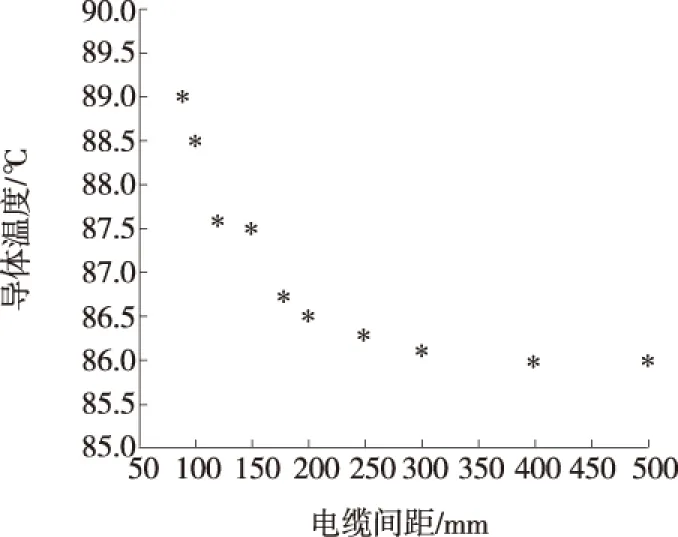
图7 导体温度随电缆间距变化曲线

3.2 不同电缆电流情形

取电缆间距为0.2 m，研究电缆发热与变化电流的关系。电流影响的是线芯损耗与金属护套损耗，绝缘介质损耗因只与电流频率有关，故即使电流值变化，交流工频50 Hz保持不变，介质损耗不变。通过计算可得，变化电流与线芯损耗、护套损耗关系如表5所示。

换算成生热率并施加在相应区域后，多次ANSYS仿真计算，得到电缆电流与埋地电缆温度场分布,如表6所示；当电流为1 050 A时，导体温度为91.8 ℃，超过允许温升；电缆电流为800 A时，埋地电缆温度场分布云图如图8所示；导体温度随电缆电流变化曲线如图9所示,可知电缆导体温度与电缆载流量趋于二次函数的关系。对于研究的电缆型号而言，载流量在1 000 A以上时，电缆发热将超越允许温升，影响电缆的运行使用寿命。

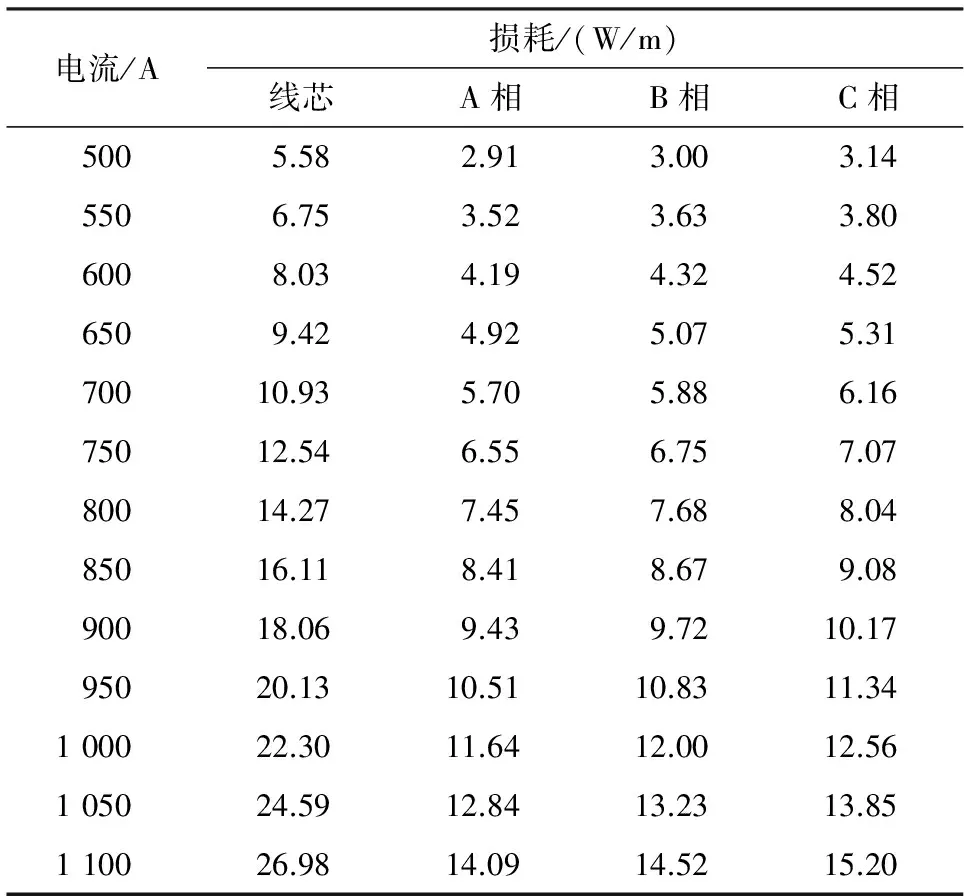
表5 电流值与线芯损耗、护套损耗数据对比

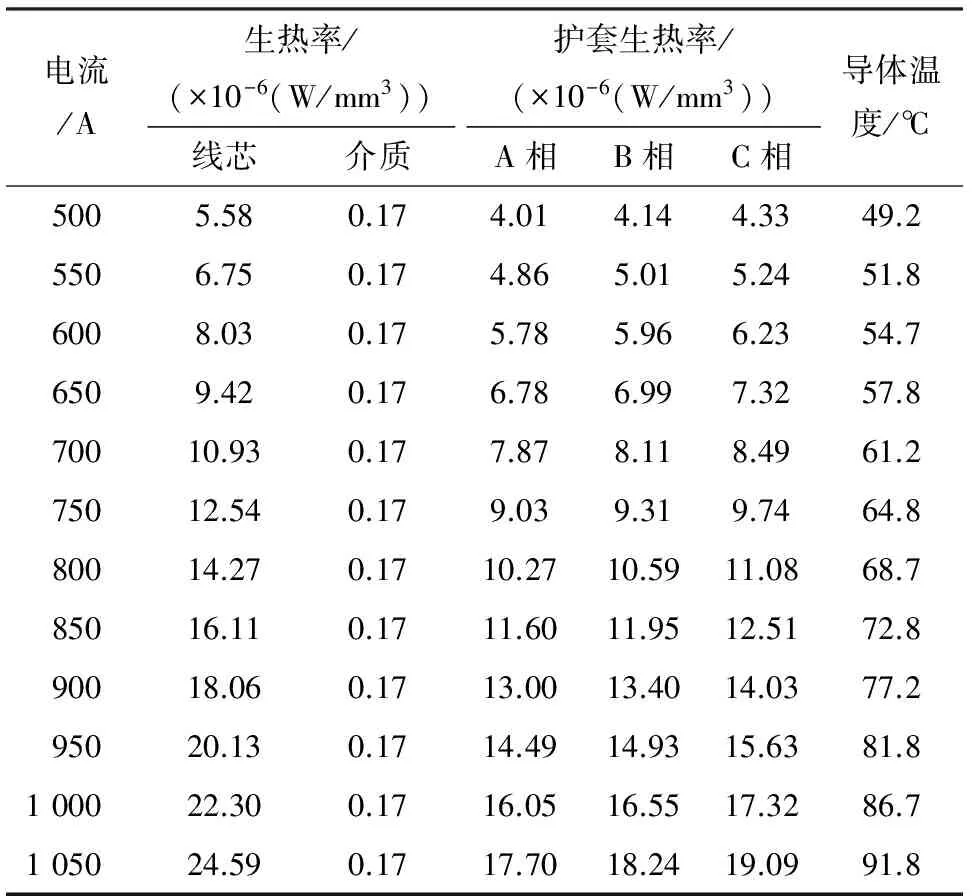
表6 电缆电流、生热率、导体温度数据对比

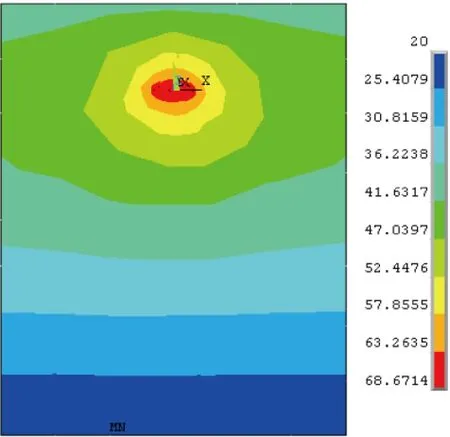
图8 电缆电流为800 A时埋地电缆温度场分布云

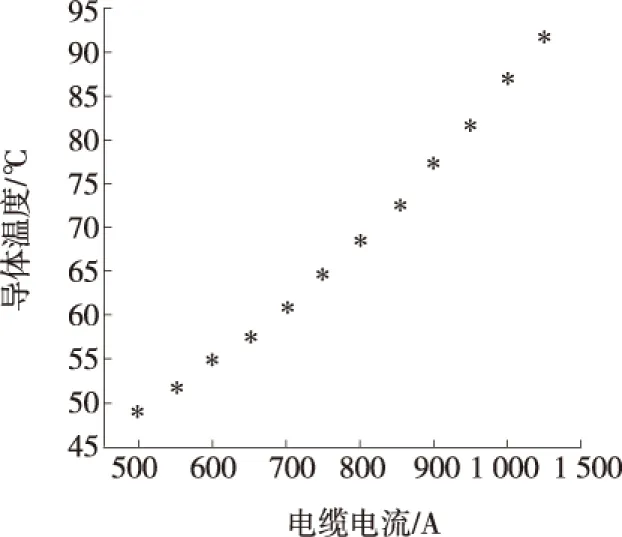
图9 导体温度随电缆电流变化曲线

4 结语

依照IEC 60287标准，理论计算电力电缆损耗基础上，基于有限元分析软件ANSYS对单回路土壤直埋电缆进行了建模仿真，并对可能影响埋地电力电缆温升发热的电缆间距与电缆载流量2个因素进行了探讨分析。

随着电缆间距的增大，电缆导体温度逐渐降低；且当电缆间距大于0.2 m时，温度变化趋于某个稳态值。电缆导体温度随着电缆载流量的升高会加速上升。电缆间距及其电缆载流量通过影响电缆各部分损耗，进而影响电缆整体生热率。

[1]周闯.利用多场耦合计算电力电缆的载流量[D]. 哈尔滨:哈尔滨理工大学，2013.

[2]罗灵琳.单芯电缆暂态温度场及载流量实时计算方法的研究[D]. 重庆:重庆大学，2008.

[3]许刚,谈元鹏,黄琳. 基于低秩矩阵填充的XLPE电力电缆寿命评估[J]. 电工技术学报,2014,29(12):268-276. XU Gang, TAN Yuan-peng, HUANG Lin. Low rank matrix completion based lifetime evaluation of XLPE power cable[J]. Transactions of China Electrotechnical Society, 2014, 29(12):268-276.

[4]梁永春, 李延沐, 李彦明, 等. 利用模拟热荷法计算地 下电缆稳态温度场[J]. 中国电机工程学报, 2008, 28(16): 129-134. LIANG Yong-chun, LI Yan-mu, LI Yan-ming, et al. Calculation of the static temperature field of underground cables using heat charge simulation method[J]. Proceedings of the CSEE, 2008, 28(16): 129-134.

[5]杨延明. 基于有限元法的电力电缆载流量计算[D]. 哈尔滨:哈尔滨理工大学，2012.

[6]吕安强,李永倩,李静,等. 光电复合海缆中光纤与导体温度关系的有限元分析方法[J]. 电工技术学报,2014,29(4):91-96. LV An-qiang, LI Yong-qian, LI Jing, et al. Finite element analysis method for temperature relationship between conductor and optical fiber in optic-electric composite submarine cable[J]. Transactions of China Electrotechnical Society, 2014, 29(4):91-96.

[7]王雄伟,张哲,尹项根,等. 多回单芯电力电缆并联运行护套感应电压的计算与分析[J]. 电力系统保护与控制,2015,43(22):77-84. WANG Wei-xiong, ZHANG Zhe, YIN Xiang-gen, et al. Calculation and analysis of sheath induced voltage for multi-circuit single-core power cable lines in parallel[J]. Power System Protection and Control, 2015, 43(22):77-84.

[8]牛海清, 王晓兵, 蚁泽沛, 等. 110 kV 单芯电缆金属护套环流计算与试验研究[J].高电压技术, 2005, 31(8): 15-17. NIU Hai-qing， WANG Xiao-bing， YI Ze-pei，et al. Study on Circulating Current of 110 kV Single-core Cable[J]. High Voltage Engineering, 2005, 31(8): 15-17.

[9]王敏. 10 kV 单相电力电缆屏蔽层的感应电压和环流[J]. 高电压技术, 2002, 28(5):30-32. WANG Min. The induced voltage and circulating current in the metal shield of 10 kV single phase electrical cables[J]. High Voltage Engineering, 2002, 28(5):30-32.

[10]贾欣, 曹晓珑, 喻明. 单芯电缆计及护套环流时载流量的计算[J]. 高电压技术,2001, 27(1): 25-26. JIA Xin, CAO Xiao-long, YU Ming. Calculation of current rate in single-core cables with circulating current[J]. High Voltage Engineering, 2001, 27(1): 25-26.

[11]徐元哲，王乐天，高洪学，等. 电力电缆接头温度场分布的理论研究[J]. 电力系统保护与控制，2008，36(24)：4-7,13. XU Yuan-zhe， WANG Le-tian，GAO Hong-xue，et al. The oretical study on temperature field distribution of power cable junction[J]. Power System Protection and Control, 2008，36(24)：4-7,13.

[12]林杰,刘刚,张海鹏,等. 架空线路并沟线夹温度分布研究[J]. 电力系统保护与控制,2013,41(24):88-94. LIN Jie, LIU Gang, ZHANG Hai-peng, et al. Research of temperature distribution of overhead lines parallel groove clamp[J]. Power System Protection and Control, 2013, 41(24):88-94.

Study on the influence factors of temperature rise in underground cable based on finite element analysis

MAO Da-jun1, XIAO Li1, LIU Guo-jian2

(1. Shanghai University of Electric Power Automation Engineering Institute，Shanghai 200090, China; 2. Zaozhuang Power Supply Company,State Grid Shandong Electric Power Company,Zaozhuang 27700, China)

When the power cable is working, the cable temperature is changed because of cable ampacity and cable spacing. The cable loss calculation formula based on the IEC standard was studied in this paper. The cable conductor loss, the insulation dielectric loss and metal sheath loss were taken as the cable internal heating source, the mode for different installation methods was established based on the finite element analysis software ANSYS, which one was single loop buried cables and another was pipe laying. The simulation results show that the temperature of cable conductor will increase when the cable load increases; the conductor temperature will reduce gradually when the cable spacing increases, and when the cable spacing is greater than 0.2m, the temperature changes will tend to a steady state.

finite element analysis; cable temperature rise; cable ampacity; cable spacing; cable loss

2016-03-19

肖 礼(1993-)，男，在读研究生，主要从事电力设备故障预警诊断研究，E-mail: shangdian_xl@163.com。

TM726.4

A

1673-9140(2016)04-0136-07