基于改进GO法的继电保护系统可靠性分析

刘宇阳，龚庆武，梁志远

(武汉大学 电气工程学院，湖北 武汉 430072)

基于改进GO法的继电保护系统可靠性分析

刘宇阳，龚庆武，梁志远

(武汉大学 电气工程学院，湖北 武汉 430072)

传统GO法已经在继电保护系统的可靠性分析中有所应用，存在计算过程繁琐，共有信号需要修正的问题。提出一种结合模糊理论与卡诺图的改进型GO法，并建立相应的继电保护可靠性分析模型。采用卡诺图简化可靠性的分析计算，降低计算错误的概率；采用模糊理论分析电力系统元件的不精确性，更真实反应系统的可靠性。改进型GO法已应用到具体的变压器继电保护系统，现场运行结果验证了该改进型GO法的优势和特色。

继电保护；可靠性分析；改进GO法；卡诺图；模糊理论

电力的供应对国家经济以及社会的稳定产生着巨大的影响，而继电保护系统是电力系统正常运行的维护者。继电保护系统能自动、快速、有选择性地将故障元件从电力系统中切除，使故障元件免于继续遭受到损害，保证其他无故障部分迅速恢复正常运行，在电力系统中发挥着重要作用，其正常工作与否将对电力系统的正常与稳定产生极大影响[1]。继电保护的不正确动作会使电力系统的故障范围扩大，甚至可能引起不良连锁故障而造成整个电力系统的瓦解与崩溃，导致电力系统的大面积停电，造成国家重大的经济损失与严重的社会影响[2]。因此，对继电保护系统的可靠性研究十分有必要且意义极其重大。

在继电保护可靠性分析中，主要有Markov模型法、故障树法、概率法、GO法等方法。美国的Kaman公司在上世纪70年代提出了GO分析法，GO法是一种系统概论分析技术，它采用图形演绎的方式，把系统流程图或原理图直接按一定规则翻译为GO图。GO法是一种以成功为导向的系统概论分析方法，它最早被应用在军事的安全性与可靠性分析方面。在上个世纪末期，GO法研究学者进一步发展了此理论，将GO法应用到了系统可靠性评估中。近十多年来，国内外学者对GO分析法进行了更加深入地研究，GO法已成功应用到了继电保护可靠性分析中。文献[3]验证了GO法在继电保护可靠性分析中的应用可能性；文献[4]研究了GO法在可修复系统中的应用前景；文献[5]验证了GO法结合simulink仿真在可修复系统中应用。

在GO法可靠性评估中，其基本步骤是将系统原理图直接翻译为GO流程图，从系统的输入事件开始，按照GO流程相关原则计算，直至得到系统最终的成功概率值。笔者提出的改进型GO法可靠性评估，核心思想是把卡诺图[6]与模糊理论[7]引入到传统GO法分析过程中。将卡诺图应用到GO法流程计算中，可以很好地解决共有信号对计算结果造成偏差的问题，降低了计算难度；将模糊三角数引入到GO法流程计算中，原因在于传统GO法是将每一个元件的概率处理为一个精确值，但这并不严谨。因为系统元件的概率是一个历史统计与运行经验的结果，很容易受到统计资料缺失及其它因素的影响。将模糊理论引入到GO法可靠性评估中，来处理系统元件概率的不准确性，可以很好地表示元件概率的模糊概率，这样得到的系统可靠性评估结果可以更真实地反应系统的可靠性。

1 卡诺图的应用

卡诺图就是逻辑函数的一种图形表示形式，先找出一个逻辑函数最小项表达式中的各最小项，再相应地填入一个方格图内，得到的方格图称为卡诺图。卡诺图的构造特点使卡诺图具有一个重要的性质：可以从卡诺图形上找出相邻的最小项，使得最小项排列得更紧凑，更便于化简。使用卡诺图最多只能化简6变量逻辑函数，卡诺图的实质是真值表的图形化。在卡诺图中，n个变量是由2n个小方格组成，卡诺图中的每一个小方块表示一个最小项，而且变量的取值顺序按格雷码排列[8]。根据此原则，可以得到2～6变量的逻辑函数卡诺图。

4变量卡诺图如表1所示，由于变量的取值顺序是按格雷码排列的，所以卡诺图具有几何位置相邻与逻辑相邻一致的特点，可以在图形中直观找出相邻最小项，并且2个相邻最小项可以合并为一个与项,达到消去一个变量的效果。先找出函数包含的所有最小项，再用“1”表示并填入变量卡诺图对应编号的小格内。

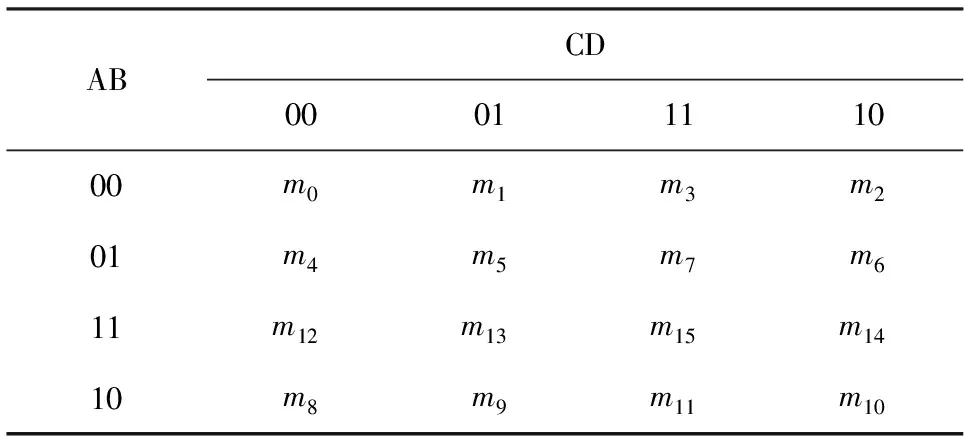
表1 4变量卡诺图

用卡诺图方法可以对逻辑函数进行化简，基本方法是用卡诺圈把相邻的最小项包围起来，即把卡诺图中相邻的“1”用卡诺圈包围起来。用卡诺图方法对逻辑函数进行化简时，关键在于卡诺圈选择的合理性。画卡诺圈的原则：①在覆盖函数所有最小项的前提下，卡诺图的圈数应尽可能小；②在满足合并规律的前提下卡诺圈应尽可能大；③根据合并的需要，每个最小项可以被多个圈包围，但每个圈内至少应有一个新的小方格。

将卡诺图应用到GO法中，主要是利用了卡诺图化简的功能。在GO法流程图中，从输入事件开始，到得到最后的系统成功概率，会有不同的路径，每一个系统元件可以表示为一个最小项，每一条路径用卡诺圈包围。通过构建系统的卡诺图，便能将GO法的计算过程简化，大大降低了计算难度。

2 模糊理论的应用

模糊性即为客观事物在属性方面的不确定性，由于事物的状态并不是唯一确定的，并且在“是”与“非”之间还存在着许多中间的状态，这些中间状态也可能存在着重合性，这种模糊性普遍存在于现实事物中。现实生活中，常常使用逻辑的 “0” 和“ 1” 表示事物的“是”与“非”，而模糊概念可以用模糊集合来表示，模糊集合是集合中的每一元素都可以用 0～1 之间的任意数值来表示，就是将具有 0 和 1 这2个值的函数F(x)扩展为可以在(0,1)区间内任意取值的连续函数P(x)，并称此函数为隶属函数[9]。隶属函数的引入很好地解决了模糊性的表示问题，通过对隶属函数的求取与分析，就可以掌握研究对象的模糊性。

在模糊理论中，隶属函数是其核心部分，隶属函数的值表示的是其隶属于集合的程度大小，这样就将集合中每一个处于“是”与“非”之间的所有中间值都表示出来，常见的隶属函数可以表示为

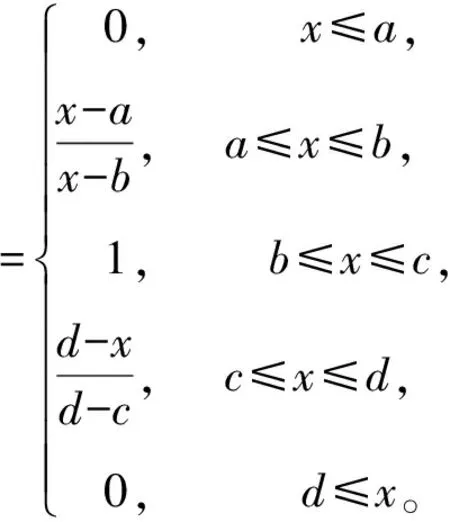
(1)

当b=c时，在隶属函数中只有一个点的隶属度值为1，故该三角模糊数可以表示为如图1所示，记为(m，α，β)，其中，m是三角模糊数的均值(m一般通过积分求取，方法并不唯一，在此不一一列举)，α与β表示的是隶属函数分布的区间大小。在实际中，α与β的取值一般根据历史统计数据、运行经验以及专家建议确定。

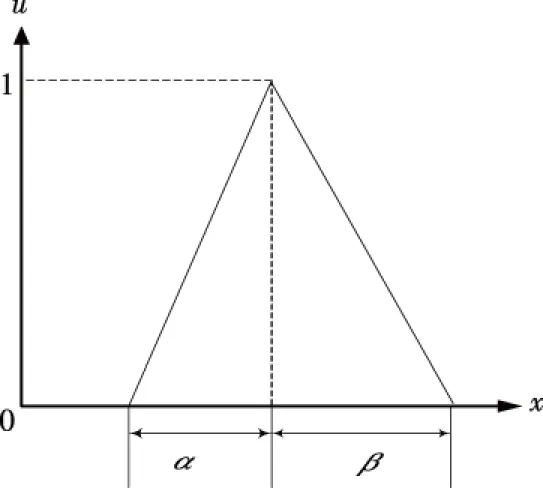
图1 三角模糊数

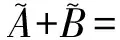
(2)

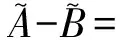
(3)

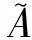
(4)

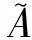
(5)

在传统的GO模型中，系统每一元件的故障概率[10]一般是由历史运行数据、运行经验和专家建议得到，但历史数据存在不全面性，运行资料也可能缺失，加上每一元件所处的外界环境的差异与随机变化性，从而导致元件的故障率具有不准确性[11]。基于上述原因，改进型GO法就将故障率的不准确性转换为模糊函数，就是将由历史数据、运行经验与专家建议所得到的系统元件故障率用模糊理论表示为模糊可能性，这样元件的概率就变为了模糊成功概率，从而就能得到系统的模糊成功概率，这样更能真实地反应系统所处的实际情况。

3 改进GO法建模

在传统GO法分析中，建模的基本思想是把系统原理图(或系统结构图)按相应的规则转换为由操作符和信号流两大要素构成的GO流程图[12]。其中，操作符表示系统每个单元的功能，以及单元输入与输出信号之间的逻辑关系，操作符的属性有类型、数据、和运算规则。类型是操作符的主要属性，操作符类型反映了操作符所代表的单元功能和特征，GO法定义了17种标准操作符[13]；信号流表示系统每个单元的输入和输出以及单元之间的关联，其属性是状态值与状态概率，在简单的两状态系统中，状态值1表示成功，状态值2代表故障，两者概率之和为1。信号流连接GO操作符生成GO图，然后依次沿着GO流程图的运算步骤进行计算，逐步运算至系统最终的输出信号，即得到系统的成功概率值。

改进型GO法的建模步骤与传统GO法一样，只是每个操作符的成功概率使用的是模糊成功概率，并在计算过程中应用了卡诺图，以便简化计算难度。在具体计算中，需要先根据系统的原理图(或结构图)搭建GO模型图，再按照相应的计算原则进行可靠性计算。

某变压器继电保护系统模型结构如图2所示，该变压器继电保护系统测量装置为2路并联配置，保证采集到的电气量信息的准确性。该变压器保护系统分为差动保护与后备保护[14]，二者对应不同的延时(TD1与TD2)，变压器故障时，差动保护优先于后备保护动作。

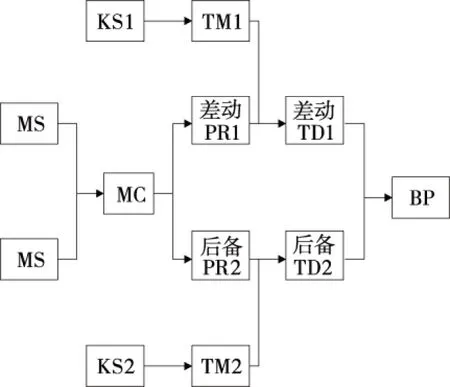
图2 变压器继电保护系统结构

由两路MS设备采集到的电气量信号，需先经过MC处理之后，继电保护装置才能接受此信号，并计算继电保护相关的电气量，判断保护动作相应逻辑，发送相应的动作信号，经延时后，断路器接收动作信号后执行跳闸等命令，切除故障设备。同时，作为相邻元件(如线路、母线)的远后备保护时，远后备信号也能经过延时装置TD，作用于断路器，执行跳闸命令。

基于图2的变压器保护系统结构图,根据GO分析法所定义的标准操作符规则[13], 系统的输入单元MS与KS以类型5操作符表示；MC,TM，PR，BR以类型1操作符表示；TD单元以类型6操作符表示；或门以类型2操作符表示。由上述表示方法，就可将变压器保护继电系统翻译为图3所示的GO图。

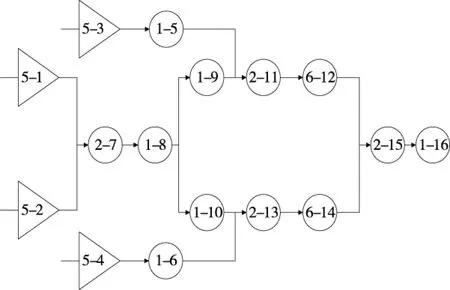
图3 变压器继电保护系统GO图

根据图3所示GO图的流程方向，结合GO操作符的运算规则与保护系统每个单元的模糊成功概率值,从输入元件开始沿着流程图逐一计算，便可得到变压器保护系统的模糊成功概率。

4 继电保护系统可靠性分析计算

4.1 模糊理论在可靠性分析中的应用

变压器继电保护系统中的每一个元件的可靠性概率，并不能片面地认为是一个定值，可以用某个模糊隶属函数表示，所以引入模糊成功概率更能准确地反映系统元件的真实水平及其可靠性[15]。一般由元件历史运行中的故障信息和技术检修人员的现场维护经验，便可以得到系统各元件的模糊成功概率值[16]。

引入模糊理论到系统可靠性分析中，使保护系统元件的可靠性不再是一个定值，而是一个模糊函数，这样就很好地解决了元件概率的不准确性，真实地反映了元件的实际工作情况，最终得到的保护系统模糊成功概率也更符合实际情况，保护系统各元件模糊可靠性概率如表2所示。

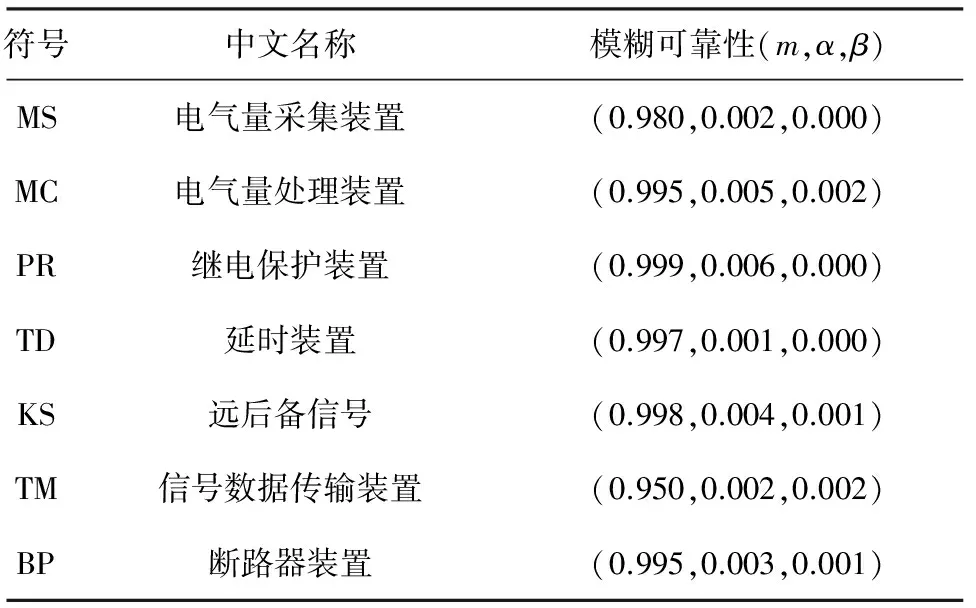
表2 系统元件模糊可靠性

4.2 卡诺图在可靠性分析中的应用

计算系统成功概率时，用Psi表示编号为i的信号流的成功概率,Pci表示编号为i的操作符的成功概率。在传统的GO算法中，一般采用的是概率公式算法，步骤是沿着GO图信号流的方向，由操作符概率计算公式直接定量,直至计算得到系统最终的成功概率值。以图3的变压器保护系统GO图模型为运算实例，详细的计算分析过程如下。

信号流7的成功概率：

Ps7=1-(1-Pc1)·(1-Pc2)，

(6)

信号流8的成功概率：

Ps8=Ps7·Pc8，

(7)

信号流9，10的成功概率：

Ps9=Ps8·Pc9，

Ps10=Ps8·Pc10，

(8)

信号流5，6的成功概率：

Ps5=Pc3·Pc5，

Ps6=Pc4·Pc5，

(9)

信号流11,13的成功概率:

Ps11=1-(1-Ps9)·(1-Ps5),

Ps13=1-(1-Ps10)·(1-Ps6)，

(10)

信号流12,14的成功概率:

Ps12=Ps11·Pc12,

Ps14=Ps13·Pc14，

(11)

信号流15的成功概率:

Ps15=1-(1-Ps12)·(1-Ps14)，

(12)

信号流16的成功概率：

Ps16=Ps15·Pc16，

(13)

Ps16即为系统的可靠性概率,将式(6)～(12)代入式(13)，整理可得：

Ps16=

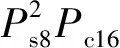
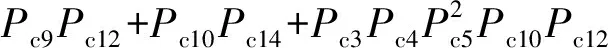
Pc5Pc10Pc14-Pc3Pc5Pc10Pc12Pc14-Pc4Pc5Pc9Pc12

Pc14)+Pc3Pc5Pc12Pc16+Pc4Pc5Pc14Pc16-Pc3Pc4

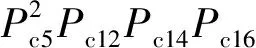
(14)

须注意的是，Ps16的表达式中存在共有信号Ps8，根据文献[12]中的原则，应该将共有信号Ps8修正,即

Ps16=

Ps8Pc16(Pc4Pc5Pc9Pc10Pc12Pc14+Pc3Pc5Pc9Pc10

Pc4Pc5Pc10Pc14-Pc3Pc5Pc10Pc12Pc14-Pc4Pc5

Pc9Pc12Pc14)+Pc3Pc5Pc12Pc16+Pc4Pc5Pc14Pc16-

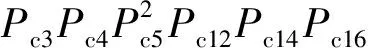
(15)

从计算过程可知，传统GO分析法存在计算过程繁琐、计算量较大的弊端，为了避免繁琐的计算过程，降低计算出错的概率，改进型GO法就将卡诺图结合到计算过程中，分析过程如图4所示。

图4 保护系统局部GO图

图3是系统完整的GO图，直接进行卡诺图分析不方便，因此将整体的保护GO图分解，用局部的GO图进行的卡诺图分析，图4即为变压器保护系统的局部GO图，利用卡诺图先求得信号流11的模糊成功概率值，再根据GO图计算原则求取变压器保护系统最终的模糊成功概率值。

信号采集元件1，2可以看作为一个元件(记为1′),该局部GO图系统包含了2条路径，分别为1′-7-8-9-11与3-5-11，元件1′的成功概率可以表示为P=1-(1-Pc1)·(1-Pc2)，图4中圆圈2-7表示或门，可以不考虑其成功概率。具体卡诺图分析如图5所示。

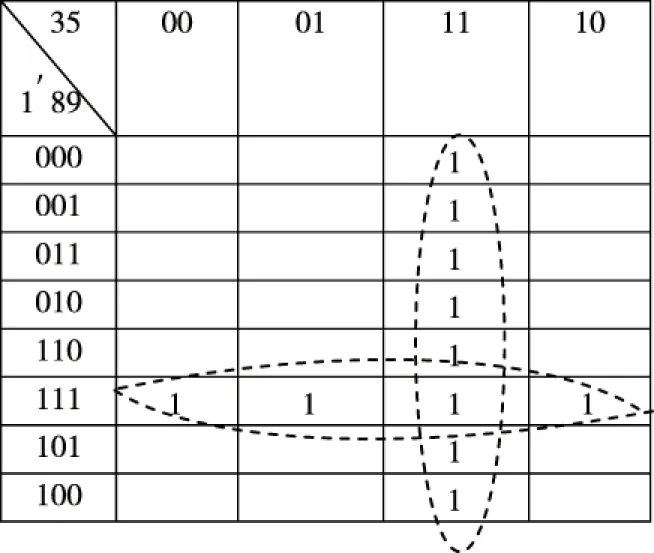
图5 卡诺图分析结果

根据卡诺图化简原则，可以得出图5的概率为

PPc8Pc9+Pc3Pc5-PPc3Pc5Pc8Pc9

即为信号流11的成功概率Ps11,得到信号流11的概率后，就可以得到系统最终的成功概率Ps16。

Ps16=Pc16[1-(1-Ps11Pc12)·(1-Ps13Pc14)]

再将表2中元件的可靠性概率带入Ps16表达式中，并结合模糊数学的运算式(2)～(5)就可以得到系统的可靠概率值(0.973,0.013,0.009)。利用传统GO分析法也能得到系统可靠性，将表2数据带入式(15)可得Ps16=0.973。改进型GO法与传统GO法计算结果对比如表3所示。

表3 不同方法得到的系统可靠性结果

通过表3可知，利用系统元件的模糊可靠性概率，可以得到系统的模糊可靠性概率范围大小，而传统GO法得到的是一个具体的数值。可见，改进型GO法得到的结果更能准确反映出变压器保护系统所处的实际水平与更真实的可靠概率。

同时，在GO图计算过程中结合了卡诺图相关原理，用图形取代了繁琐的公式，使计算流程更加直观，过程更加简洁，避免了繁琐的计算，降低了计算出错的概率，而且还能避免共有信号的修正问题，得到的结果同样准确。

5 结语

笔者针对传统GO法在可靠性分析中存在的问题，将基于卡诺图与模糊理论的改进型GO法引入到继电保护可靠性分析中，并通过具体的变压器保护系统建立了模型。

通过建模计算可知，用模糊理论表示系统元件的故障概率能很好地解决元件故障概率的不准确性，通过计算最终得到的变压器保护系统可靠性概率是一个区间值，更能准确反映出保护系统所处的实际可靠值。在计算可靠性过程中，可以对GO图运用卡诺图相关原理，用图形取代繁琐的公式，避免计算公式太过繁琐，减小计算出错概率。改进型GO法在变压器继电保护系统可靠性评估中的应用，可以得到系统可靠性概率区间，且计算过程简便，结果能更真实反映系统的可靠性水平。

[1]马成连,孙黎,尚教会. 抗灾型电网安全风险评估方法研究[J]. 电网与清洁能源,2014,30(9):12-18. MA Cheng-lian, SUN Li, SHANG Jiao-hui. Safety risk assessment method of power grid[J]. Power System and Clean Energy, 2014,30(9):12-18.

[2]孙志媛,李海波,鲁宗相. 考虑连锁故障的大电网可靠性评估[J]. 电力科学与技术学报, 2015,30(1):67-72. SUN Zhi-yuan, LI Hai-bo, LU Zong-xiang. Consider a cascading failure of large power grid reliability evalution[J]. Electric power science and technology, 2015,30(1):67-72.

[3]王超. GO法在继电保护可靠性评估中的初步应用[J]. 电力系统自动化,2007,31(24):52-56. WANG Chao. The preliminary application of the GO method in the reliability analysis of relay protection system[J]. Automation of Electric Power Systems, 2007,31(24):52-56.

[4]沈祖培,黄祥瑞，高佳. 可修系统可靠性分析中GO法的应用[J].核动力工程, 2000,21(5):456-461. SHEN Zu-pei，HUANG Xiang-rui,GAO Jia. GO method has is employed in the reliability analysis of repairable system[J]. Nuclear Power Engineering, 2000,21(5):456-461.

[5]黄涛,蔡琦. Simulink仿真技术在压水堆净化系统可靠性GO法分析中的应用[J]. 核动力工程, 2010,31(1):88-91. HUANG Tao, CAI Qi. Simulink simulation technology in the GO method reliability analysis of PWR purification system[J]. Nuclear Power Engineering, 2010,21(1):88-91.

[6]董金明,张艳晓. 卡诺图化简法在逻辑函数中的应用[J]. 信息与电脑,2013(5):157-158. DONG Jin-ming, ZHANG Yan-xiao. Karnaugh map reduction method in the application of logic function[J]. Information and Computer, 2013(5):157-158.

[7]郑圆圆,陈再良.模糊理论的应用与研究[J]. 苏州大学学报,2011,31(1):52-58. ZHENG Yuan-yuan, CHEN Zai-liang. The application of fuzzy theory and research[J]. Journal of Suzhou University, 2011, 31(1):52-58.

[8]雷升印.多输出组合逻辑函数共卡诺图化简法的研究[J]. 武汉理工大学学报,2001, 23(2):7-9. LEI Shen-ying. Multi-output combinational logic function of karnaugh map reduction method research[J]. Journal of Wuhan University of Technology, 2001, 23(2):7-9.

[9]胡圣武.基于模糊理论的GIS质量评价与可靠性分析[D]. 武汉：武汉大学,2004.

[10]郭创新,陆海波,俞斌,等. 电力二次系统安全风险评估研究综述[J]. 电网技术,2013,37(1):112-118. GUO Chuang-xin, LU Hai-bo, YU Bin, et al. Overview of power two system security risk assessment studies[J]. Power Grid Technology, 2013,37(1):112-118.

[11]雷春燕,刘从法,罗日成. 基于多目标智能加权灰靶理论的电力变压器状态维修决策[J]. 电力科学与技术学报,2013,28(2):85-88. LI Chun-yan, LIU Cong-fa, LUO Ri-cheng. Based on multi-objective weighted grey target theory of intelligent power transformer state maintenance decisions[J]. Electric Power Science and Technology, 2013,28(2):85-88.

[12]王超, 高鹏,W SHAO. GO在继电保护可靠性评估中的应用[J]. 电力系统自动化,2007,31(21):52-56. WANG Chao, GAO Peng, W SHAO. The application of relay protection reliability evaluation[J]. Automation of Electric Power Systems, 2007,31(21):52-56.

[13]沈祖培,黄瑞祥. GO原理及应用到一种可修复系统可靠性分析方法[M]. 北京：清华大学出版社,2004.

[14]刘威. 合理选择配电变压器的保护配置[J]. 电力系统保护与控制,2010,10(3):66-71. LIU Wei. Reasonable selection of distribution transformer protection configuration[J]. Power System Protection and Control, 2010,10(3):66-71.

[15]郭磊. 考虑输电设备可靠性的电网风险分析研究[D].杭州:浙江大学,2012.

[16]李军智.基于GO法的牵引变电所可靠性研究[D]. 成都：西南交通大学,2009.

Reliability analysis for protection system with the advanced GO method

LIU Yu-yang，GONG Qing-wu，LIANG Zhi-yuan

(School of Electrical Engineering, Wuhan University, Wuhan 430072, China)

Traditional GO method has been applied in the reliability analysis of power system protection system, but it has some shortage, such as, onerous calculation and shared signals modification. An advanced GO method combined with fuzzy theory and karnaugh map was proposed, and the corresponding relay protection reliability analysis model was established in this paper. By using the karnaugh map, the calculation of reliability analysis was simplified and the calculation error probability was reduced. By using the fuzzy theory to deal with the inaccuracy of system components, the degree of system reliability could be authentic shown. Finally, the advanced GO method was applied to a specific transformer relay protection system, and the precise quantitative analysis was carried out. Comparing with the traditional method, the advanced GO method in relay protection is with high availability and reliability.

power system protection; reliability analysis; advanced GO method; Karnaugh Map; fuzzy theory

2016-05-26

龚庆武(1967—)，男，博士，教授，主要从事电力系统运行与控制、优化与调度的研究; E-mail：gongqingwu_67@163.com

TM732

A

1673-9140(2016)04-0129-07