基于谱估计和粒子群算法的电压闪变计算方法

吴丹岳

(国家电网福建省电力有限公司 电力科学研究院，福建 福州 350007)

基于谱估计和粒子群算法的电压闪变计算方法

吴丹岳

(国家电网福建省电力有限公司 电力科学研究院，福建 福州 350007)

间谐波的注入会导致电压的均方根值和峰值发生波动从而引起闪变，基于调幅波模型的闪变检测模型的测量精度较差。提出一种基于谱估计算法和粒子群算法的间谐波闪变检测方法。首先，通过比值法确定电压信号中不同频率分量的个数，再利用谱估计算法确定各分量的准确频率；然后，利用粒子群算法确定各个分量的幅值和相角，计算间谐波闪变值。仿真结果表明：该方法对于调幅波闪变信号和间谐波闪变信号，以及两者的混合闪变信号，均能快速准确地检测间谐波参数并计算闪变值。

闪变；间谐波；谱估计算法；粒子群算法

随着社会的发展，电网的复杂程度日益提高，大量的波动性负荷并网运行会造成电网功率较大的波动，产生电压波动和闪变问题，这是电力系统中电能质量的一大威胁，因此必须采用有效方法对闪变进行检测和评估。

目前，在闪变的检测和评估上应用最为广泛的是IEC闪变仪模型[1-2]，该模型所采用的测量方法主要有：平方检测法、整流检测法和有效值检测法[3]。近年来也出现了一些新的算法，如小波分析法[4]、独立分量法[5]、Hilbert-Huang变换法[6]等，但这些方法都是基于电压调幅波模型分析电压的闪变效应，模型中考虑的调幅波频率范围在0.05～35 Hz，因此，IEC闪变仪模型无法对频率在15～85 Hz之外的间谐波引起的闪变进行准确检测[7-8]。而这些频率的间谐波的注入也会导致电压波形的有效值和峰值产生变化，进而引起闪变[8]。随着电网中间谐波含量的增加，间谐波对闪变的影响不可忽略。

间谐波闪变效应的计算，关键在于间谐波参数的准确求取。文献[9]将调幅波转化为一对间谐波的叠加，文献[10]进一步提出“AM-间谐波对”和“PM-间谐波对”的概念，即调幅波可以视为间谐波的特例。因此，不失一般性，可直接通过检测间谐波计算电压的闪变效应。文献[11]分析了单个间谐波对有效值波动和峰值波动的影响，但是没有分析多个间谐波存在时对闪变的影响。文献[12]提出了含有多个间谐波时闪变效应的频域算法，但是要求针对间谐波重新设计视感度加权滤波器。文献[13]提出一种基于频率搜索的间谐波闪变效应计算方法，能够有效地检测出频谱相互干扰的2个间谐波的参数，提高了多个间谐波成分下的频率分辨率。文献[10]利用一种非同步采样下的奇数频点插值修正法测量电压信号中各频率分量的参数，能够有效地分离信号中的谐波和间谐波成分，抑制它们之间的频谱干扰。

近年来，谱估计算法在间谐波参数估计上得到广泛应用，如文献[14-15]均利用Root-MUSIC算法估计信号的频率。其中，文献[14]利用遗传算法估计间谐波参数，但遗传算法实现较为复杂，计算量大，而文献[15]利用Adaline神经网络估计间谐波参数，其估计精度易受估计频率的影响，且神经网络实现复杂。

笔者从间谐波角度出发，分析调幅波与间谐波之间的相互转化关系，建立基于间谐波的电压闪变信号模型。为了更为准确地估计间谐波参数，首先采用比值法和谱估计算法中的MUSIC算法确定电压信号中不同频率的分量个数及各分量的频率，然后利用基于杂交的粒子群算法对各个分量的幅值和相角进行估计，进而计算闪变值。仿真算例分别对一般闪变信号和含有间谐波的复杂闪变信号进行检测。经过仿真验证，该文所提方法能够有效地检测出信号中各个频率分量的参数，实现过程简单可行，估计结果的精度较高。

1 电压闪变信号模型

对电压闪变信号进行建模时，必须兼顾调幅波和间谐波的影响。

电压闪变的调幅波模型：

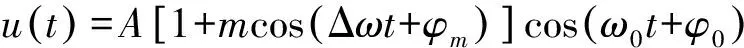
(1)

式中A为基波电压幅值；ω0为基波电压角频率；m为调制系数；Δω为电压调幅波角频率；φ0为基波电压初相位；φm为电压调幅波初相位。

利用三角变换公式对式(1)进行展开，可得到

(2)

式中f0为基波电压频率，ω0=2πf0；fm为电压调幅波频率，Δω=2πfm；m1，m2，f1，f2，φ1，φ2分别为调幅波转化为间谐波的幅值、频率和相角，其中，m1=m2，f1=f0+fm，f2=f0-fm，φ1=φ0+φm，φ2=φ0-φm。

式(2)表明，调幅波可以转化为基波和一对间谐波的叠加，并且，间谐波对具有幅值相等、频率相对于基波频率对称的特点，因此可将调幅波视为间谐波的特例。

以上分析了调幅波与间谐波对的相互转化关系，对于间谐波不成对存在的情况，如：

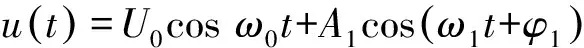
(3)

当间谐波的幅值满足关系式A1/U0≪1时，式(3)可以表示为

(4)

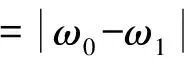
基于以上分析，调幅波与间谐波可以相互转化，因此，在对电压闪变信号进行建模时，可采用基波和间谐波叠加的形式进行建模。同时，考虑到电压信号中可能含有谐波，将电压信号模型表示为

(5)

式(5)中第1项表示基波电压，第2项表示谐波，第3项表示间谐波。其中，M表示信号中含有的谐波分量的个数，M=0表示信号中不含有谐波分量，mi，fi，φi分别表示第i个谐波分量的幅值、频率和相角；N表示信号中含有的间谐波分量的个数，N=0表示信号中不含有间谐波分量，nj，fj，fj分别表示第j个间谐波分量的幅值、频率和相角。

2 基于谱估计算法的电压信号频率估计

在进行谐波分析时，离散傅里叶变换(DFT)具有物理意义明确、计算量小的特点，能够很好地解决谐波检测问题。但当电压信号中含有间谐波时，采样频率需要取值很大才能保证较高的频率分辨率，否则DFT的结果会存在频率泄露效应，使检测结果出错，因此，DFT在间谐波的检测中的应用受到了限制。而谱估计算法则具有很高的频率分辨率，且精确度很高，能够很好地解决间谐波的频率检测问题。本文采用谱估计算法中的MUSIC算法[16-17]对间谐波的频率进行检测。由于MUSIC算法的频率估计精度受到设定的信号源数的影响，因此，该文采用比值法对信号源数进行估计。

2.1 利用MUSIC算法估计信号频率

假设电压信号为p个不同频率分量的叠加，即

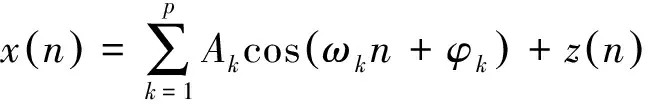
(6)

式中Ak和ωk分别为第k个分量的幅值和相角；ωk为归一化角频率，ωk=2πfk/fs，fs为工频；z(n)是噪声信号。

利用该信号的采样点序列构造长度为m的观察矩阵，记为

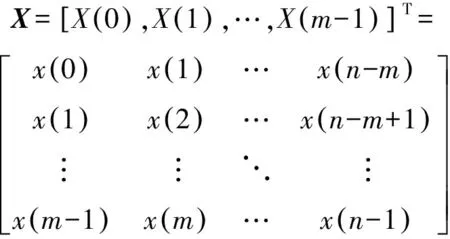
(7)

根据三角函数的和差公式，有

(8)

则式(7)可表示为

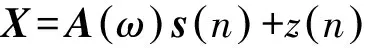
(9)

其中，

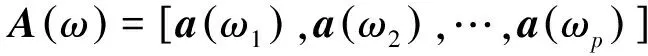
(10)

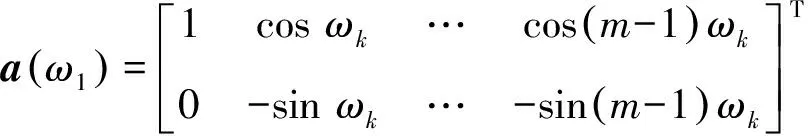
(11)

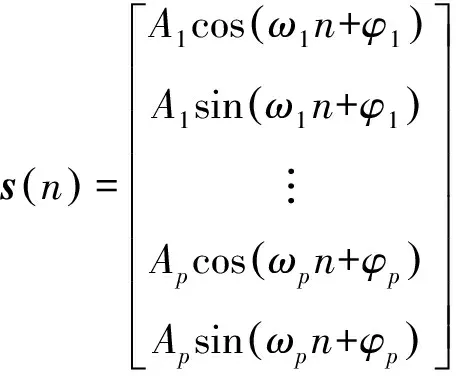
(12)

其中，p为信号源数。在实际应用中，m应大于2p，且m越大，估计精度越高，但所需计算时间也越长。

构造空间协方差矩阵RXX：

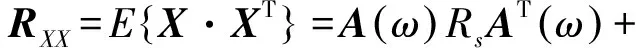
(13)

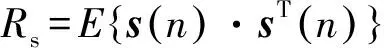
对RXX进行特征值分解：

(14)

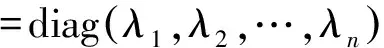
由于信号和噪声子空间存在空间正交性，因此，信号子空间的方向向量与噪声子空间也存在正交性，即

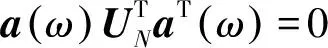
(15)

根据以上分析，可以通过空间谱的峰值估计信号频率，定义函数pMUS如下：

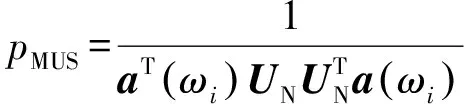
(16)

在实际应用中，通常将ωi划分成为数百个等间距的单位，得到ωi=2πτfi，如取fi=0.001，然后将每个ωi值代入式(16)，求出所有fi对应的峰值。

2.2 信号源数估计

利用MUSIC算法估计信号频率时，如果估计的信号源数小于实际信号源数，则估计得到的空间谱中峰值个数偏少，也会使峰值的位置偏移；如果估计的信号源数大于实际信号源数，则估计得到的空间谱中峰值个数可能会偏多，即产生“假峰”。因此，准确地估计信号源数是MUSIC算法估计精度的有效保证。

如果能够知道真正的协方差矩阵，则由其小特征值相等就可以准确地估计出信号源数，即信号子空间维数。然而在实际应用中，由于得到的样本数据是有限的，因而真正的协方差矩阵是获取不到的，只能得到协方差矩阵的估计，而且其小特征值是互不相等的。该文采用比值法确定信号源数：

根据式(10)～(12)的分析，RXX的主特征值应有2p个，其余(m-2p)个小特征值应比主特征值小得多，定义d1=λ2/λ1，d2=λ3/λ2，…，dm-1=λm/λm-1，计算

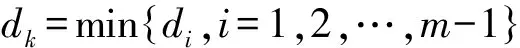
(17)

当dk最小时，说明λk≫λk+1，则信号源数为p=k/2。

3 基于粒子群算法(PSO算法)的间谐波幅值估计

3.1 基于PSO算法的间谐波幅值检测模型

利用比值法和MUSIC算法确定电压信号中含有的分量个数和各个分量的频率之后，可以构建电压信号模型(式(5))，模型中待求解的参数为各个分量的幅值和相角。理论上，必然存在一组最优的模型参数，使得构造的电压信号模型的波形与待检测电压信号的波形完全一致，即为所求的真实解。为了对比2个电压波形是否一致，可分别对2个信号进行采样对比，取值点越多，对比结果越精确，但计算量也越大。

首先，选择待检测电压信号的N个离散点序列作为波形对比的基准，记为

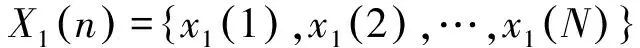
(18)

式中x1(i)为待检测电压信号的瞬时值。

对构造的电压信号波形以相同的采样频率进行采样，采样长度取为N，记为

(19)

理论上，2个信号的起始采样时刻可以不同。当起始采样时刻不同时，模型参数优化的结果仅在初相角上有所不同，而各频率的幅值不变，但为简单起见，本文对2个信号均从过零点开始采样，则优化目标为

(20)

目标函数越接近0，则优化得到的模型参数越接近真实值。该文利用基于杂交的PSO算法对模型参数进行优化求解。

3.2 基于杂交的PSO算法原理

粒子群优化算法(PSO)是Kennedy博士在1995年提出的一种群体智能优化算法，能够实现复杂空间的寻优过程。PSO算法可直接利用粒子的位置代表优化问题的解，根据粒子的位置直接计算目标函数值得到适应度值，直接评价每个粒子的优劣程度。

该算法开始时将问题初始化为一个随机粒子群，这些粒子在每次迭代过程中通过跟踪个体最优解和全局最优解来不断更新自身的位置，进而寻找到问题的最优解。以一个D维问题的求解为例，设粒子数为m，则粒子的位置和速度分别表示为

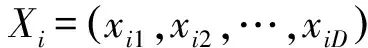
(21)

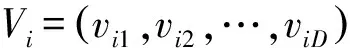
(22)

基本PSO算法的寻优过程可以表示为

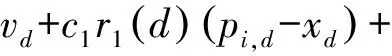
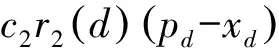
(23)

xd+1=xd+vd+1。

(24)

式(23)、(24)中xd，vd分别为第d次迭代时粒子的位置和速度；pi,d，pd分别为第d次迭代时粒子群的个体最优解和全局最优解；w为惯性权重；c1，c2为学习因子或加速常数；r1(d)，r2(d)为[0,1]之间的随机数。

基本粒子群算法的结构简单、速度快，但在处理复杂优化问题时，容易陷入局部最优，出现早熟收敛现象，因此，借鉴遗传算法中的杂交概念，在每次迭代时，根据杂交概率选取指定数量的粒子放入杂交池内，池中的粒子随机两两杂交，产生同样数目的子代粒子(child)，并用子代粒子替换亲代粒子(parent)。子代位置由父代位置进行算术交叉得到：

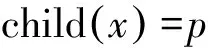
(25)

其中，p是0～1之间的随机数。

子代的速度计算为

·。

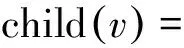
(26)

基于杂交的PSO算法能够有效地避免算法陷入局部最优而出现早熟，提高算法的收敛精度。

3.3 利用谱估计和PSO算法检测闪变的步骤

利用谱估计和基于杂交的PSO算法计算电压闪变的步骤如下：

1)利用比值法确定待检测电压信号的信号源数，即信号中含有的不同频率分量的个数，设其中谐波分量个数为M，间谐波分量个数为N；

2)利用MUSIC算法确定待检测电压信号中各个分量的确定频率；

3)根据步骤2中得到的各频率，建立电压闪变信号模型，未知变量为各个分量的幅值和相位，则未知变量的个数为2(M+N+1)；

4)随机初始化种群中各粒子的位置和速度，其中，表示幅值的粒子的值应大于0，表示相位粒子的值取[-π,π]；

5)根据2.1节所述的原理对各个粒子进行计算，得到各个粒子的适应度值；

6)评价各粒子的优劣程度，获得粒子的个体极值和种群的全局极值；

7)根据杂交概率选取指定数量的粒子放入杂交池内，池中的粒子随机两两杂交产生同样数目的子代粒子，子代的位置计算公式如式(25)，速度计算公式如式(26)；

8)判断是否达到最大迭代次数或预设的计算精度，若是，则终止寻优过程，否则，开始下一次的迭代过程；

9)优化结束，得到待检测电压信号中各频率分量的幅值和相角；

10)根据闪变值计算原理，计算电压闪变值。

4 仿真算例

4.1 一般闪变信号

为验证算法有效性，该文采用Matlab进行仿真计算。假设有一调幅波形式的闪变信号，共含有2种频率的调幅波，信号表达式：

(27)

在采样频率fs=4 000 Hz，采样数据长度N=400时，利用该文提出的方法对信号进行检测。首先利用比值法进行分析，然后利用MUSIC和PSO算法分别估计各分量的频率、幅值和相角。检测结果如表1所示，并与实际值进行比较，计算其误差水平。

表1 一般闪变信号检测结果及误差数据

从表1计算结果可以看出，信号中共含有5个频率分量，观察其频率和相角可知，分量2和4为一个间谐波对，对应于第1个调幅波分量；分量1和5是另一个间谐波对，对应于第2个调幅波分量。频率估计结果说明：结合比值法和MUSIC算法的信号频率估计精度很高，这就确保了利用PSO算法估计各分量幅值和相角的准确度，因为如果频率估计结果误差较大，则建立的电压信号模型本身就存在误差，PSO算法的寻优结果必然出现更大误差。仿真过程中也发现，MUSIC算法对频率的估计精度不仅影响PSO算法的参数估计精度，而且还影响算法的寻优时间。

得到各间谐波的频率和幅值后，就可以根据式(4)转化为调幅波，求得电压波动值ΔV，进而计算其瞬时闪变值S(t)，最后根据短时间闪变水平计算公式计算Pst以确定闪变效应。

4.2 复杂闪变信号

假设有一复杂闪变信号，既含有调幅波分量，又含有间谐波分量，信号表达式：

(28)

该信号引起的闪变为调幅波和间谐波分别与基波调制引起的闪变效应的总和。

首先利用比值法进行分析，得到信号中含有的不同频率分量个数为4，然后利用MUSIC和PSO算法分别估计各分量的频率、幅值和相角。检测结果如表2所示，并与实际值比较，计算其误差水平。

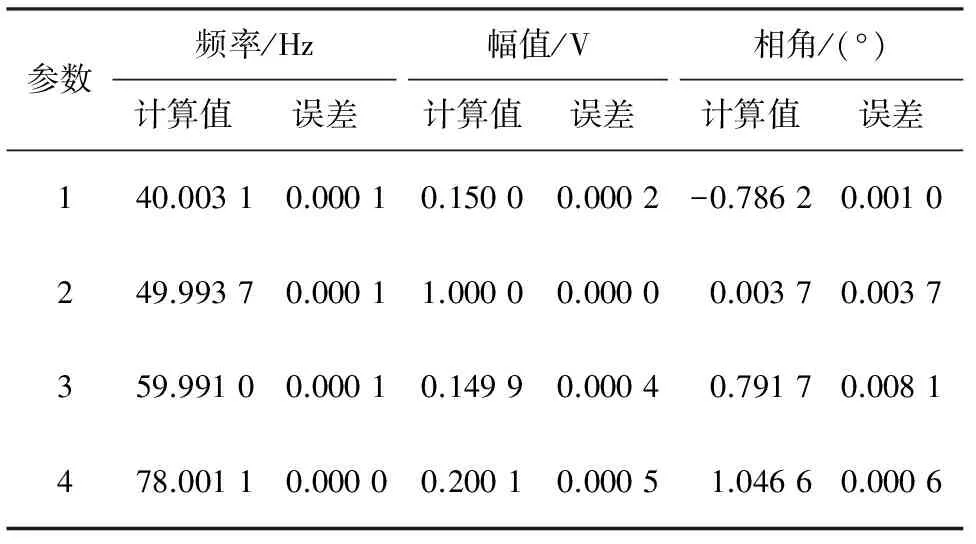
表2 复杂闪变信号检测结果及误差分析

从表2计算结果可以看出，对于含有调幅波和间谐波的复杂闪变信号，间谐波的频率、幅值和相角的估计结果依然准确，即建立的模型不受引起闪变的信号类型的影响。

另外，通过分析计算结果可知，PSO算法对间谐波幅值的估计精度要比对相角的估计精度来得高，而在计算闪变效应时，所需数据为间谐波幅值，因此，这一不足不影响该方法的使用。

4.3 频率估计精度对幅值估计精度的影响

MUSIC算法的频率估计结果对构建电压信号模型至关重要，将直接影响PSO算法的寻优精度。以3.2中的复杂闪变信号为例，分别仿真分析频率估计结果在不同的频率偏差量下的幅值估计精度。PSO算法的最大迭代次数取为5 000次，将优化得到的模型参数结果与实际值进行比较，计算得到各分量幅值的相对误差，取4个幅值中误差最大的一个进行分析，绘制出“频率估计偏差量-幅值估计相对误差”曲线，如图1所示。

图1 频率估计偏差量-幅值估计相对误差关系曲线

从图1中可以看出，随着频率估计偏差量的增大，幅值估计的相对误差也随着增大，这是由于构建的电压信号模型的精确度随着频率估计偏差量的增大而增大，较难找到一组模型参数使得构造的电压信号波形与检测的电压信号完全一致，因此，PSO算法的优化结果只能使2个信号尽可能一致。

当频率估计偏差量大到一定程度的时候，基于PSO算法辨识得到的间谐波幅值将是错误的，无法用于闪变效应计算，因此，必须保证MUSIC算法的频率估计精度。

5 结语

笔者首先分析了电压闪变信号模型，提出一种基于谱估计和PSO算法的间谐波型闪变计算方法。该方法先后利用比值法、MUSIC和PSO算法分析得到间谐波分量的个数、频率、幅值和相角信息，进而直接计算间谐波型闪变值。

该方法的频率分辨率由MUSIC算法决定，而实践表明MUSIC算法具有很高的频率分辨率，在2个间谐波分量频率靠得较近的情况下，不存在频谱混叠现象，频率辨识精度依然很高。基于PSO算法的参数辨识方法利用寻优的思想寻找一组近于最优的幅值和相角参数，使得构造的波形与检测波动接近于一致，在频率辨识精度较高的情况下，幅值和相角辨识精度也很高。

文中利用一个简单闪变信号和一个复杂闪变信号对所提出的方法进行仿真分析，结果说明了该方法具有很高的计算精度。同时，仿真了频率估计精度对幅值估计精度的影响，指出基于PSO算法的模型参数辨识对频率估计精度依赖性很强，因此保证频率估计精度对保证该方法的计算精度是十分必要的。

[1]IEC 868—1986.Flickermeter-functional and design specification[S].

[2]IEC 61000—4—15—1997. Flicker meter-functional and design specifications[S].

[3]孙树勤. 电压波动与闪变[M]. 北京: 中国电力出版社, 1999.

[4]周兆经，周文晖，李青. 采用小波分解和同步检波的电压闪变信号检测新方法[J]. 电力系统及其自动化学报，2001, 13(6): 23-27. ZHOU Zhao-jing，ZHOU Wen-hui，LI Qing．A new method for the detection of voltage flicker using wavelet transform and synchronous detection[J]．Proceedings of the CSU-EPSA，2001，13(6)：23-27.

[5]刘阳，杨洪耕. 基于独立分量分析的电压闪变检测方法[J]. 电力自动化设备，2007, 27(11): 34-37. LIU Yang，YANG Hong-geng．Voltage flicker detection based on independent component analysis[J]．Electric Power Automation Equipment，2007，27(11)：34-37.

[6]王志群，朱守真，周双喜. Hilbert变换求取电压闪变有关参数[J]. 电力系统自动化，2004, 28(5): 34-37. WANG Zhi-qun，ZHU Shou-zhen，ZHOU Shuang-xi．Parameter estimation of voltage flicker through Hilbert transform[J]．Automation of Electric Power Systems，2004，28(5)：34-37.

[7]马永强，张有玉，武剑. IEC闪变仪对间谐波引起的电压闪变测量误差的分析[J]. 电力系统保护与控制，2010, 38(1): 23-27. MA Yong-qiang，ZHANG You-yu，WU Jian．Analysis of the IEC flicker meter measurement error for measuring inter harmonic caused voltage flickers[J]．Power System Protection and Control，2010，38(1)：23-27.

[8]陶骞，王碧芳. 间谐波对电压闪变检测影响的研究[J]. 电测与仪表，2011, 48(4): 45-48. TAO Qian，WANG Bi-fang．Study of the impact on voltage flicker detection caused by inter-harmonics[J]．Electrical Measurement &Instrumentation，2011，48(4): 45-48.

[9]张全明，刘会金，兰泉妮，等. 基于频谱分析的间谐波闪变效应计算[J]. 电力系统自动化，2009, 33(9): 67-72. ZHANG Quan-ming，LIU Hui-jin，LAN Quan-ni，et al．Calculation of interharmonic-caused flicker based on spectrum analysis[J]．Automation of Electric Power Systems，2009，33(9)：67-72.

[10]李霏霏，杨洪耕，惠锦，等. 通过间谐波测量计算闪变值的方法研究[J]. 电工电能新技术， 2011, 30(4): 50-55. LI Fei-fei,YANG Hong-geng,HUI Jin，et al. Research of calculation of flicker values based oninter-harmonics measurement[J]. Advanced Technology of Electrical Engineering and Energy，2011，30(4):50-55.

[11]Tayjasanant T, Wang Wencong, Li Chun, et al. Interharmonic-flicker curves[J]. IEEE Transactions on Power Delivery，2005, 20(2): 1 017-1 024.

[12]王建勋，刘会金. 间谐波闪变效应计算及闪变源识别方法[J]. 电力系统自动化， 2011, 35(12): 52-58. WANG Jian-xun，LIU Hui-jin．A calculation method for interharmonic scaused flicker and flicker source identification[J]．Automation of Electric Power Systems，2011，35(12)：52-58.

[13]周菁菁，王彭，赵春宇，等. 基于频率搜索的间谐波闪变检测方法[J].电力系统自动化，2014, 38(7): 60-65. ZHOU Jing-jing，WANG Peng，ZHAO Chun-yu，et al. A detection method of interharmonics-caused flicker based on frequency-serching[J].Automation of Electric Power Systems，2014, 38(7): 60-65.

[14]高培生，谷湘文，吴为麟. 基于求根多重信号分类和遗传算法的谐波间谐波频谱估计[J]. 电工技术学报，2008, 23(6): 109-113. GAO Pei-sheng，GU Xiang-wen，WU Wei-lin.Harmonic andinterharmonic spectrum estimation based on Root-MUSIC and GA[J]．Transactions of China Electrotechnical Society，2008，23(6)：109-113.

[15]陈国志，蔡忠法，陈隆道. 基于Root-MUSIC和Adaline神经网络的间谐波参数估计[J]. 浙江大学学报：工学版，2011, 45(1): 173-177. CHEN Guo-zhi，CAI Zhong-fa，CHEN Long-dao．Interharmonic parameter estimation based on Root-MUSIC and Adaline neural network[J]．Journal of Zhejiang University:Engineering Science，2011，45(1):173-177.

[16]程志友，刘阳. 基于求根MUSIC算法的电压闪变参数估计[J]. 电工电能新技术，2013, 32(1): 23-27. CHENG Zhi-you，LIU Yang. Parameter estimation of voltage flicker based on Root-MUSIC[J].Advanced Technology of Electrical Engineering and Energy，2013, 32(1): 23-27.

[17]孙向文，孙立功. 用于电力系统谐波频率高分辨估计的MUSIC算法[J]. 电测与仪表，2008, 45(10): 19-21,32. SUN Xiang-wen，SUN Li-gong．Sign correlation function based modified music algorithm for harmonic frequency estimation in power system[J]．Electrical Measurement & Instrumentation，2008，45( 10): 19-21，32．

Voltage flicker calculation method with spectral estimation and PSO algorithm

WU Dan-Yue

(State Grid Fujian Electric Power Research Institute, Fuzhou 350007，China)

The RMS and peak of voltage is changed by inter-harmonic, which will lead to flicker, and the measurement accuracy of voltage flicker is low. A voltage flicker of inter-harmonic calculation method with the spectral estimation and particle swarm optimization was presented in this paper. Firstly, the ratio method was used to determine the number of different frequency components. Secondly, the PSO algorithm was applied to determine the amplitude and phase angle of each component, and then the voltage flicker was calculated. Simulation results show that the amplitude modulation signal, inter-harmonic signal and their mixed flicker signal, inter-harmonic parameters can be effectively and quickly measured, and voltage flicker can also be calculated accurately.

flicker; inter-harmonic; ratio method; spectral estimation algorithm; PSO algorithm

2016-10-30

国家电网公司科技项目(SGRI-DL-71-15-006)

吴丹岳(1964—)，男，硕士，高级工程师，主要从事电能质量分析、网源协调、电网安全稳定等方向的研究；E-mail: wudanylx@sina.com

TM714

A

1673-9140(2016)04-0018-08