剑麻珊瑚混凝土挠度曲线及应力应变曲线研究★

莫 倩 刘存鹏*

(1.广西交通职业技术学院，广西南宁 530023; 2.桂林理工大学南宁分校，广西南宁 530001)

剑麻珊瑚混凝土挠度曲线及应力应变曲线研究★

莫 倩1刘存鹏2*

(1.广西交通职业技术学院，广西南宁 530023; 2.桂林理工大学南宁分校，广西南宁 530001)

通过建立荷载—挠度曲线模型，拟合了不同剑麻纤维掺量下珊瑚混凝土的荷载—挠度曲线，并研究了其应力—应变全曲线随剑麻掺量的变化关系，采用两段式表达了剑麻纤维珊瑚混凝土应力—应变全曲线。

剑麻纤维，珊瑚混凝土，挠度曲线，应力应变曲线

0 引言

不破坏当地生态环境，用海水代替淡水，珊瑚砂代替粗骨料或者细骨料配制而成的珊瑚混凝土在土木工程和军事工程上具有重大的现实意义。要解决其实际应用问题就必须研究其力学性能，应力—应变全曲线和挠度曲线是影响研究珊瑚混凝土变形性能的两个重要因素，本文通过试验研究拟合了不同剑麻纤维掺量下珊瑚混凝土的荷载—挠度曲线，研究其应力—应变全曲线随剑麻掺量的变化关系，为剑麻纤维珊瑚混凝土在其他领域的应用提供参考。

1 试验概况

1.1 原材料及配合比

水泥的强度等级为P.O42.5;砂为普通的天然河砂;水为拌合的海水;粗骨料为珊瑚砂，其级配良好，筒压强度为1.98 MPa，吸水率为16.5%;剑麻纤维的长度为15 mm左右。参照JGJ 51—2002轻骨料混凝土技术规程进行配合比设计，剑麻纤维珊瑚混凝土的设计强度等级为C30。

1.2 试验方案

本试验的荷载—挠度曲线采用了三点弯曲试验来完成，立方体试件的边长为150 mm，其中跨中切口深度25 mm。测试时，速率采用0.2 mm/min，采用恒位移控制为其控制方式，试样跨距500 mm，试验机器则为具有闭环控制能力的电液伺服试验机;应力—应变全曲线试验采用的试验机器为LAXW500型微机控制电液伺服刚性试验机，轴向压力和纵向变形均由计算机在试验过程中自动采集，在正式加载前每个试块都进行3次预加载，加载时采用4.4×10－5s－1等应变控制，采用试块在中部100 mm标距范围内的压缩量作为纵向变形值。

2 试验结果分析

2.1 挠度曲线试验分析

1)荷载—挠度曲线模型。目前，国内外很多学者对于压缩状态下的混凝土的应力—应变曲线提出了各自的模型，比如:过镇海模型［1］、YiST模型［2］、徐世模型［3］和张德思模型［4］。其中，第一个模型相比于其他模型所具有的优点就是模型具有较少的待定参数，且具有明确的数学意义。

在弯曲状态下不同掺量剑麻珊瑚混凝土所获得的荷载—挠度曲线的形态如图1所示。

图1 荷载—挠度曲线

本试验的模型以过镇海模型作为基础，建立了弯曲状态下的剑麻纤维珊瑚混凝土的荷载—挠度曲线模型，见式(1)和式(2):

上升段:

下降段:

其中，y=F/Fpeak;x=δ/δpeak;A，B均为最小二乘方法情况下拟合后的系数。

2)荷载—挠度曲线模型的拟合。采用最小二乘拟合的方法，利用上述的载荷—挠度曲线模型对实测的荷载—挠度曲线进行拟合，结果见图2。用在拟合的荷载—挠度曲线下的面积与在实测的荷载—挠度曲线下的面积的差值除以在拟合的荷载—挠度曲线下的面积所得的百分数作为面积差异百分数，如式(3)所示。从表1可见，拟合荷载—挠度曲线和实测荷载—挠度曲线下的面积差异百分数不超过10%。结果表明，该荷载—挠度曲线模型适合用来拟合实测的荷载—挠度曲线。

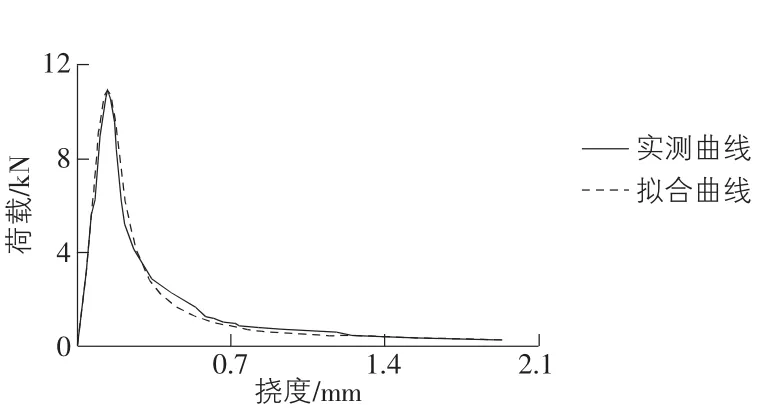
图2 典型的实测和拟合所得荷载挠度曲线

其中，ΔS为面积差异百分数;S拟为在拟合的荷载—挠度曲线下的面积;S实为在实测的荷载—挠度曲线下的面积。

表1 面积差异百分数

2.2 应力—应变全曲线试验分析

每种剑麻纤维掺量选取三个试块测试其应力—应变全曲线，结果如图3～图7所示。

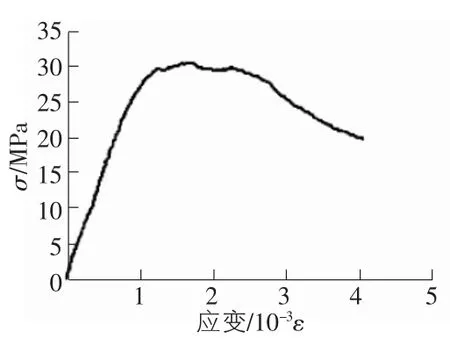
图3 纤维掺量为0的应力—应变曲线

图4 纤维掺量为1.5 kg/m3的应力—应变曲线

图5 纤维掺量为3 kg/m3的应力—应变曲线

图6 纤维掺量为4.5 kg/m3的应力—应变曲线

图7 纤维掺量为6 kg/m3的应力—应变曲线

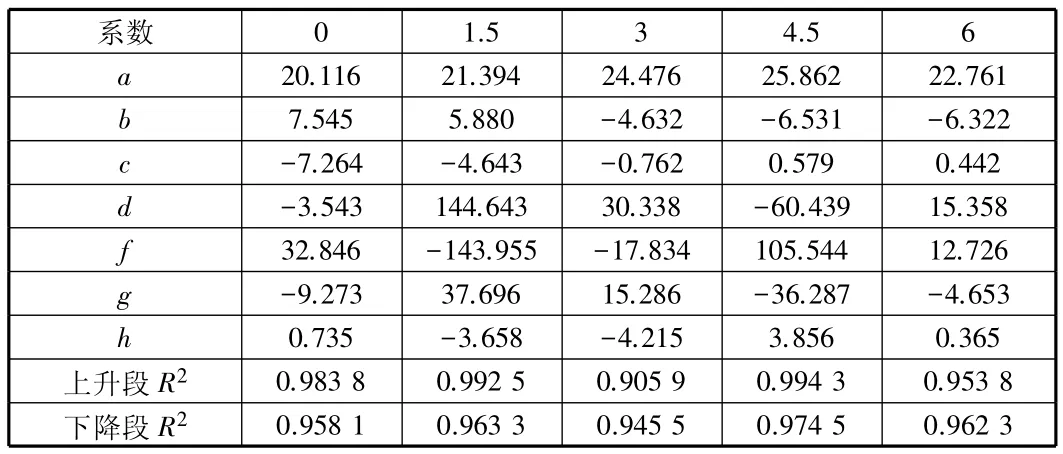
表2 不同纤维掺量下珊瑚混凝土应力应变曲线参数拟合结果

由图3～图7可见，剑麻纤维珊瑚混凝土应力—应变全曲线包含了两段曲线，即上升段和下降段，当剑麻纤维掺量增加时极限应变随之增加，而极限应力却随之降低。采用分段拟合表达式拟合其应力应变曲线，见式(4)，式(5)，系数的拟合结果如表2所示，根据表2的数据可知，该相关系数R2与1很接近，也就是说拟合曲线和试验点吻合的效果比较好。

3 结语

1)对于剑麻纤维珊瑚混凝土的荷载—挠度曲线模型，本文所建立模型对实测曲线具有较好的拟合能力;

2)剑麻纤维珊瑚混凝土与普通混凝土的应力—应变曲线类似，当剑麻纤维掺量增加时，极限应变随之增加，而极限应力却随之降低;

3)因为珊瑚骨料具有特殊性，建议不同掺量下剑麻纤维珊瑚混凝土的应力—应变曲线表达式采用上升段与下降段的两段式来表达，实测数据与结果较为匹配。

［1］过镇海，张秀琴.混凝土在反复荷载作用下的应力—应变全曲线［J］.工业建筑，1981(9):14-17.

［2］YIST，KIMJK，OHTK.Effect of strength and age on the stressstrain curves of concrete specimens［J］.Cement and Concrete Research，2003，33(8):1235-1244.

［3］王利民，徐 世.混凝土及纤维混凝土材料特性曲线［J］.大连理工大学学报，2002，42(5):580-585.

［4］张德思.混凝土应力—应变全曲线的试验研究［J］.湖南大学学报(自然科学版)，1982，9(4):58-72.

Research on deflection curve and stress-strain curve of sisal coral concrete★

Mo Qian1Liu Cunpeng2*
(1.Guangxi Communications and Vocational Technical College，Nanning 530023，China; 2.Nanning Branch，Guilin University of Technology，Nanning 530001，China)

Through the establishment of load-deflection curve model，this paper fitted the load-deflection curve of coral concrete with different sisal fiber content，and researched the change relationship its stress-strain whole curve with sisal content，using two stages expression of the stressstrain curve of sisal fiber coral concrete.

sisal fiber，coral concrete，deflection curve，stress-strain curve

TU528

:A

1009-6825(2016)36-0131-03

2016-10-18 ★:2015年度广西高校科学技术研究项目一般项目(项目编号:KY2015YB505);2016年度广西高校中青年教师基础能力提升项目(项目编号:KY2016YB908)

莫 倩(1988-)，女，助教

刘存鹏(1988-)，男，硕士，讲师