基于经验模态分解和模糊机会约束的混合储能容量配置方法

曹 超，马玉鑫，常 悦，关瑞丰

(上海电气集团中央研究院，上海 静安 200070)

基于经验模态分解和模糊机会约束的混合储能容量配置方法

曹 超，马玉鑫，常 悦，关瑞丰

(上海电气集团中央研究院，上海 静安 200070)

为了进行储能容量配置，采用经验模态分解方法，从频域上对储能功率进行划分，并分配给能量型电池和功率型电池，以储能成本最小为约束，以修正系数作为模糊变量，建立模糊机会约束模型，并用于模糊模拟的遗传算法求解。通过仿真算例得出储能电池和超级电容器系统的容量和功率，达到了储能容量配置的要求，采用混合储能系统可以满足平滑风电功率波动的要求，同时充分发挥储能电池和超级电容器的特性，将储能电池和超级电容器的荷电状态控制在合理范围内，保证了储能系统能够稳定运行。

新能源；风力发电；混合储能平滑；容量配置；遗传算法

0 引言

风力发电具有随机性、间歇性、不可控性，会出现发电功率不稳定，其规模化并网将给电网的安全稳定经济运行以及电网的电能质量造成不利的影响[1-3]。

近年来，混合储能系统控制策略和容量配置引起了人们的关注。混合储能系统包括能量型储能电池和功率型储能电池，通过功率型电池容量小、寿命长、功率密度高等特点辅助大容量、相对循环次数受限、能量密度高、功率密度低的能量型储能电池，根据频率特性利用储能电池进行分类补偿，相比单类型储能电池而言更加具有系统性能和经济性[4-5]。

目前，混合储能系统的研究主要集中在控制策略上或者容量配置的研究中，综合考虑控制策略和容量配置的相关研究较少。文献[6]利用饱和控制理论对维持系统稳定的最小储能容量进行计算。文献[7]中的方法考虑了混合储能装置的功率出力和荷电状态约束。文献[8]中的方法利用雨流计数法和等效循环寿命理论，充分考虑了系统在整个运行生命周期内的各项成本，并通过此模型得到成本最小时混合储能系统的额定功率和额定容量。

本文采用经验模态分解方法，将储能功率从频域上进行划分并分配给能量型电池和功率型电池，以储能功率修正系数作为模糊变量，储能系统成本最小为目标，建立模糊机会约束模型，并采用模糊模拟的遗传算法求解。满足风电并网功率波动的要求，同时充分发挥储能电池和超级电容器的特性，将储能系统荷电状态(state of charge, SOC)控制在合理范围内，保证了储能系统能够稳定运行，提高了储能电池的使用寿命。

1 混合储能系统模型及控制策略

1.1 混合储能结构

混合储能系统结构如图1所示，主要由风电机组、逆变器、储能电池、超级电容器、交流母线组成，能量型电池和超级电容器与逆变器相连，逆变器与交流母线相连接，风电场通过风电逆变器与交流母线相连。图中：PWG表示风力发电系统输出功率；Pout表示风储联合发电系统输出到电网的功率；混合储能系统输出或吸收的功率为PHESS=PWG-Pout；混合储能电池输出功率等于储能电池和超级电容器功率之和，公式为PHESS=Pbat+Pcap，Pbat为能量型电池输出功率，Pcap为功率型电池输出功率。如果PHESS>0，储能电池处于充电状态，如果PHESS<0，储能电池处于放电状态。

本文采用储能电池和超级电容器进行混合储能的容量配置，其价格性能参数如表1所示，储能电池具有能量密度大、价格便宜的优点，但同时又存在电池容量有限，循环使用寿命短、充放电效率低、响应速度慢的缺点，而超级电容器具有充电时间短、贮存寿命长、功率密度高、循环使用次数多、传输效率高的特点，但是存在价格昂贵、容量密度大的缺点。将2类电池结合起来进行混合储能容量配置，充分发挥储能电池和超级电容器的特性进行协调控制，可以弥补单一类型存在的缺点。

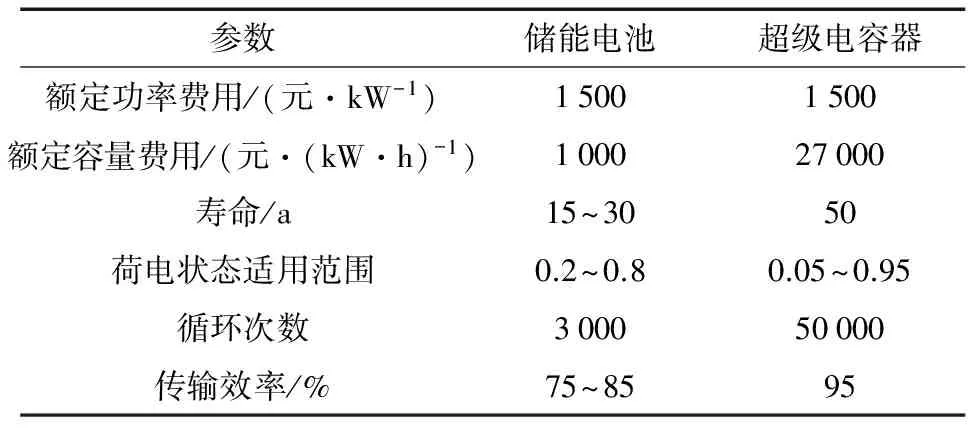
表1 混合储能装置参数Table 1 Parameters of hybrid energy storage system

1.2 混合储能控制策略

本节采取斜率限制的方法对风电功率进行平滑控制[9-10]，可以满足波动率的控制要求，t时刻的功率变化值公式为

(1)

目标功率值是根据以下的规则实现：

(2)

式中：

(3)

(4)

并网风电功率：

(5)

(6)

(7)

对得出的储能系统总功率信号PHESS做经验模态分解(empirical mode decomposition, EMD)，分成若干个固有模态函数，将k阶之后的所有本征模态函数(intrinsic mode function, IMF)之和的低频部由储能电池吸收，从第1阶到第k阶的IMF之和为高频部分分量，由超级电容器进行吸收，充分发挥超级电容器动态响应快的特性。k为对储能系统总功率信号进行EMD分解并计算其标准化模量累积均值得出的滤波阶数基准值[11-13]。

(8)

(9)

采用斜率控制和经验模态分解相结合的储能平滑控制，能够在一定程度上降低并网波动率，结合风电波动率的情况，理论上如果配置足够大的储能容量，满足约束条件，这样一定能满足控制要求，但因为储能成本比较昂贵，这样会极大地增加成本。可以在部分情况下不满足约束条件，也就是使约束条件满足的概率不小于某一置信水平，这样考虑更加具有实际意义和工程价值，本文选取基于模糊机会约束规划的方法进行优化储能容量配置。

2 混合储能装置优化配置模型

2.1 模糊机会约束规划理论

机会约束规划是随机规划的3个分支之一，1959年查纳斯(A.Charnes)和库伯(W.W.Cooper)提出机会约束规划理论，一般的机会约束规划的问题可以转化为确定性模型和机会约束模型，但对于较复杂的机会约束规划问题，给出的解在实际过程中无法实现。采用模糊机会约束虽然给出的也是一个确定性的解，但只要求这个解在实际问题中尽可能地执行。

文献[14]针对微网系统中利用储能系统处理电能质量问题，这里采用机会约束的方法进行混合储能容量配置，以储能成本最小为目标，使用遗传算法进行求解不确定模型，得到混合储能的功率和容量的配置结果。将机会约束规划的方法应用在储能容量配置的问题上，更具实际意义。

文献[15-16]运用机会约束解决了配电网中的不确定因素，为配电网规划设计人员提供了一种选择的方法。

文献[17]将模糊机会约束规划运用在含风电场的电力系统优化调度问题上，以风电场有功出力预测值与实际发电功率之间存在的误差作为模糊数，采用模糊遗传算法进行求解，仿真实例证明了该策略的有效性和灵活性。

带有模糊参数的数学规划可以写成如下形式：

(10)

式中：x为决策变量，ξ为模糊参数变量，f(x,ξ)为目标函数，gj(x,ξ)≤0为约束函数。这个模糊规划的数学意义并不明确，这是因为ξ为模糊向量而导致符号min以及约束没有定义。

模糊参数机会约束规划的理论框架形式如下：

(11)

式中b为实现给定的约束目标的置信水平；Cr表示{.}中事件的可能性。加入模糊数，可以使算法更加具有灵活性[18]。

2.2 储能优化控制的数学模型

在本文风电场和混合储能组成联合发电系统中，混合储能系统的目的是将风电平滑率限制在一定区间范围内，同时满足储能SOC和功率限值约束，采用模糊机会约束规划的目的是由于储能装置成本的问题，如果要求100%满足约束条件，就会造成高额的储能成本代价，可以使约束条件满足的概率在某一置信水平下，使得在储能成本最小和约束条件中找到折中的结果。

2.2.1 功率修正系数作为模糊数

(12)

(13)

(14)

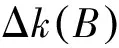
2.2.2 模糊机会约束数学模型

本文考虑储能成本作为目标函数，为了简化计算，忽略了储能电池的生产成本、维护成本，考虑其容量和功率成本。

(15)

式中：Eb和Eu分别为储能电池和超级电容器的容量；WSOCbmin、WSOCbmax分别为储能电池储能装置荷电状态上下限；WSOCumin、WSOCumax分别为超级电容器荷电状态上下限；C为混合储能装置总成本费用；a为风电平滑率区间范围；Cpb、Cpu分别为储能电池和超级电容器的额定功率单价；Ceb、Ceu分别为储能电池和超级电容器额定容量单价。

2.3 基于模糊模拟的遗传算法求解

根据数学模型，采用基于模糊模拟的遗传算法流程如下所述(见图2)。

步骤(1)：读入相关数据，首先是风电出力数据和风电平滑功率数据，其次是储能的特性，包括储能电池最大充放电功率值、混合储能荷电状态的最大值和最小值，再次是遗传算法的一些参数，包括种群大小、迭代次数、交叉和变异率等。

步骤(2)：初始化种群，产生初始群体包括群体的编码方式和群体的产生方式2个方面，采用模糊模拟的方法进行储能功率和容量的初始化。

步骤(3)：对每条染色体进行仿真。

步骤(4)：检验每个染色体是否满足机会约束条件，如满足，则进入步骤(5)，如都不满足则进行变异运算形成新一代染色体种群，执行步骤(3)。

步骤(5)：选取满足机会约束条件的染色体，计算其对应的目标函数值，即混合储能配置成本。

步骤(6)：对种群中的染色体进行变异和交叉操作；使用模糊模拟检验后代的可行性，得到新一代染色体。

步骤(7)：判断是否达到最大迭代次数，达到则停止计算，否则重复步骤(3)—(6)。

步骤(8)：将最好的染色体作为混合储能最优配置方案。

3 仿真分析

本文采用Matlab进行仿真分析，选取某50 MW风电场2011年某天实际运行功率数据为例，储能电池和超级电容器的初始WSOC设置为0.5，储能电池荷电状态WSOC最大值为0.8，最小值为0.2，超级电容器的荷电状态WSOC最大值为0.95，最小值为0.05。

仿真过程采用选取置信水平a=90%进行分析，得到的混合储能优化配置方案如下，其中储能电池功率为3.8 MW，储能电池容量为19.25 MW·h，超级电容的功率为2.9 MW，超级电容的容量为1.1 MW·h。利用混合储能进行平滑，从图3可以发现，采用混合储能进行平滑控制后，可以将波动率控制在要求范围内，提高了电能质量。图4为平滑波动率曲线，可以发现采用混合储能平滑可以将波动率控制在10%以下。

图5为储能电池和超级电容器功率曲线图。由图5可知，超级电容器波动性比较大，补偿了混合储能系统中高频部分，而储能电池系统比较平缓地补偿低频部分。由图5可以发现在超级电容器配合下，储能电池充放电周期大，说明储能电池的充放电次数减少，可以提高储能电池的寿命，稳定了储能电池SOC。

图6为储能电池和超级电容的SOC状态曲线，由图6可以看出，储能电池和超级电容的SOC都能控制在要求内，这样可以避免储能电池过度充电和过度放电对储能设备的影响，稳定了储能电池SOC，提高了整个系统的稳定性。

4 结论

本文提出了一种平抑光伏功率波动的方法，基于模糊聚类模态经验分解，将光伏功率信号分解成低频、高频信号。将低频分量作为光伏并网功率，高频分量由储能电池吸收，以平抑光伏功率波动。为较好地平滑光伏波动率并且稳定储能荷电状态，将平滑后波动率和储能电池荷电状态作为约束条件，采用模糊自适应控制的方法，调节EMD滤波阶数以平滑光伏输出。仿真分析证明了本文所提控制策略的有效性。与采用定阶EMD平滑进行比较，平滑波动效果更好，储能荷电状态SOC更加稳定，可以将波动率控制在5%以内，减小了光伏波动给电网带来的影响，同时可以稳定储能电池SOC，实现储能系统性能指标和波动率指标的协调优化。

[1] 周孝信， 鲁宗相， 刘应梅， 等． 中国未来电网的发展模式和关键技术[J]． 中国电机工程学报， 2014， 34(29)： 4999-5008． ZHOU Xiaoxin， LU Zongxiang， LIU Yingmei， et al． Development models and key technologies of future grid in China[J]． Proceedings of the CSEE， 2014， 34(29)： 4999-5008．

[2] 李建林， 田立亭， 来小康． 能源互联网背景下的电力储能技术展望[J]． 电力系统自动化， 2015， 39(23)： 15-22． ． LI Jianlin， TIAN Liting， LAI Xiaokang， et al． Outlook of electrical energy storage technologies under energy internet background [J]． Automation of Electric Power Systems， 2015， 39(23)： 15-22．

[3] 胡娟， 杨水丽， 侯朝勇， 等． 规模化储能技术典型示范应用的现状分析与启示[J]． 电网技术， 2015， 39(4)： 879-885． HU Juan， YANG Shuili， HOU Chaoyong， et al． Present condition analysis on typical demonstration application of large-scale energy storage technology and its enlightenment[J]． Power System Technology， 2015． 39(4)： 879-885．

[4] LI X． Fuzzy adaptive Kalman filter for wind power output smoothing with battery energy storage system[J]． IET Renewable Power Generation， 2012， 6(5)： 340-347．

[5] LI X， LI J， XU L， et al． Online management of lithium-ion battery based on time-triggered controller area network for fuel-cell hybrid vehicle applications[J]． Journal of Power Sources， 2010， 195(10)： 3338-3343．

[6] 韩涛， 卢继平， 乔梁， 等． 大型并网风电场储能容量优化方案[J]． 电网技术， 2010， 34(1)： 169-173． HAN Tao， LU Jiping， QIAO Liang， et al． Optimized scheme of energy-storage capacity for grid-connected large-scale wind farm[J]． Power System Technology， 2010， 34(1)： 169-173．

[7] 吴云亮， 孙元章， 徐箭， 等． 基于饱和控制理论的储能装置容量配置方法[J]． 中国电机工程学报， 2011， 31(22)： 32-39． WU Yunyao， SUN Yuanzhang， XU Jian， et al． Determination methodology for energy storage capacity based on saturation control theory[J]． Proceedings of the CSEE， 2011， 31(22)： 32-39．

[8] 韩晓娟， 程成， 籍天明， 等． 计及电池使用寿命的混合储能系统容量优化模型[J]． 中国电机工程学报， 2013， 33(34)： 91-97． HAN Xiaojuan， CHENG Cheng， JI Tianming， et al． Capacity optimal modeling of hybrid energy storage systems considering battery life[J]． Proceedings of the CSEE， 2013， 33(34)： 91-97．

[9] YOSHIMOTO K， NANAHARA T， KOSHIMIZU G． New control method for regulating state-of-charge of a battery in hybrid wind power/battery energy storage system[C]//Power Systems Conference and Exposition， Atlanta， 2006： 1244-1251．

[10] 孟顺， 谢桦， 基于经验模态分解的平滑可再生能源功率波动的储能容量优化[J]． 电源学报， 2014， 5(5)： 7-11． MENG Shun， XIE Hua． Energy storage capacity optimization in smoothing renewable energy power fluctuation based on empirical mode decomposition[J]． Journal of Power Supply， 2014， 5(5)： 7-11．

[11] 韩晓娟， 陈跃燕， 张浩， 等． 基于小波包分解的混合储能技术在平抑风电场功率波动中的应用[J]． 中国电机工程学报， 2013， 33(19)： 8-13． HAN Xiaojuan， CHEN Yueyan， ZHANG Hao， et al． Application of hybrid energy stor age technology based on wavelet packet decomposition in smoothing the fluctuations of wind power [J]． Proceedings of the CSEE， 2013， 33(19)： 8-13．

[12] PATRICH F， GABRIEL B， PAULO G． Empirical mode decomposition as a filter bank[J]． IEEE Transactions on Signal Processing Letters， 2004， 11(2)： 112-114．

[13] LI X， HUI D， LAI X． Battery energy storage station (bess)-based smoothing control of photovoltaic (PV) and wind power generation fluctuations[J]． IEEE Transactions on Sustainable Energy， 2013， 4(2)： 464-473．

[14] 谢石骁， 杨莉， 李丽娜． 基于机会约束规划的混合储能优化配置方法[J]． 电网技术， 2012， 36(5)： 79-84． XIE Shixiao， YANG Li， LI Lina， et al． A chance constrained programming based optimal configuration method of hybrid energy storage system[J]． 2012， 36(5)： 79-84．

[15] 雷亚洲， 王伟胜， 印永华， 等． 基于机会约束规划的风电穿透功率极限计算[J]． 中国电机工程学报． 2002． 22(5)： 32-35． LEI Yazhou， WANG Weisheng， YIN Yonghua， et al． Wind power penetration limit calculation based on chance contrained programming[J]． Proceedings of the CSEE， 2002． 22(5)： 32-35．

[16] 赵国波， 刘天琪， 李兴源， 等． 基于灰色机会约束规划的输电系统规划[J]． 电网技术， 2009， 33(1)： 22-25． ZHAO Guobo， LIU Tianqi， LI Xingyuan， et al． Power transmission system planning based on grey chance constrained programming[J]． Power System Technology， 2009， 33(1)： 22-25.

[17] 杨宁， 文福栓． 基于机会约束规划的输电系统的规划方案[J]． 电力系统自动化， 2004， 28(14)： 23-27．

YANG Ning， WEN Fushuan． Transmission system expansion planning based on chance constrained programming[J]． Automation of Electric Power Systems， 2004， 28(14)： 23-27．

[18] YUE Xiaofeng， SHAO Haihe． Fault diagnosis of rolling element bearing based on improved ensemble empirical mode decomposition[C]//Proceedings of International Conference on Intelligent Human-Machine Systems and Cybernetics． Hangzhou： IEEE， 2015： 52-55．

马玉鑫(1988—)),男，博士，研究方向为分布式能源大数据和储能技术；

常 悦(1990—)，女，硕士，研究方向为分布式能源大数据和储能技术；

关瑞丰(1990—)，男，硕士，新能源发电技术和通信技术。

(编辑 蒋毅恒)

Capacity Allocation Method of Hybrid Energy Storage System Based on Empirical Mode Decomposition and Fuzzy Chance Constrained Programming

CAO Chao， MA Yuxin， CHANG Yue， GUAN Ruifeng

(Central Research Academy of Shanghai Electric Group, Jingan District, Shanghai 200070, China)

Empirical mode decomposition (EMD) method was introduced to make capacity configuration for the hybrid energy storage system (HESS), dividing the energy storage power in frequency domain and assigning to energy density and power density batteries. Capacity allocation model, based on fuzzy chance constrained programming, was built with the minimum annual cost and state of charge(SOC) confidence level as constraints. The fuzzy simulation-based genetic algorithm was used to solve the fuzzy model. The capacity and power of storage battery and super capacitor were obtained by simulation calculation. The hybrid energy storage system can be introduced to smooth the fluctuations of wind power-output and control the load of storage battery and super capacitor, so as to guarantee the stable operation of storage system.

new energy; wind power; hybrid energy storage system(HESS) smoothing; capacity allocation; genetic algorithm

TK81;TM911

： A

： 2096-2185(2016)03-0043-06

2016-08-16

曹 超(1990—)，男，硕士，研究方向为新能源发电控制技术和储能技术,caochao8010@163.com；