考虑桩身自重影响的超长桩屈曲分析

唐文栋，刘晓钊

（1. 安徽省建筑科学研究设计院，安徽 合肥 230041；2. 江苏大学 土木工程与力学学院，江苏 镇江 212013）

考虑桩身自重影响的超长桩屈曲分析

唐文栋1，刘晓钊2

（1. 安徽省建筑科学研究设计院，安徽 合肥 230041；2. 江苏大学 土木工程与力学学院，江苏 镇江 212013）

由于超长桩的桩身自重较大，其对超长桩稳定性有重要影响。已有的研究大多只考虑桩侧土抗力的影响，能同时考虑桩侧土抗力和桩身自重两个影响因素的超长桩屈曲荷载计算公式目前还很少报道。本文同时考虑桩侧土抗力和桩身自重的影响，通过选择合适的桩身挠曲变形函数及桩侧土弹性抗力模式，基于能量法给出了顶部有集中荷载、部分埋置于Winkler地基中超长桩的屈曲荷载和计算长度的解析表达。最后分析了桩侧土抗力和桩身自重对屈曲荷载的影响。结果表明桩侧土抗力是影响屈曲荷载的主要因素。当桩身埋置率（h/L）较低时，桩身自重对屈曲荷载的影响不容忽视；但随埋置率的增加，桩身自重对屈曲荷载的影响甚微。

屈曲分析；超长桩；临界荷载；瑞利-里兹法；桩身自重

0 引 言

基桩的稳定性分析是一个古老而又非常具有实际工程意义的问题。随着我国大型基础设施建设的快速发展，近年来在我国东部沿海地区，大量的高层建筑和特大型桥梁的基桩长度已超过百米。置于软弱地基中的超长桩可能发生失稳破坏如细长杆件，因此超长桩基础的应用使桩的稳定性得到了进一步的重视。

有关桩屈曲分析国内外有不少解答，如考虑地基系数为常数的Timoshenko解、考虑成层地基系数的Davisson和Robinson模拟计算机解[1]，文献[2]给出了完全埋入桩的能量法解答等。国内研究起步较晚，在吸收国外理论和试验分析基础上，文献[3]考虑桩侧土弹性抗力，用迦辽金法得到高承台桩和低承台桩的临界荷载解析解。文献[4,5]采用最小势能原理及变分法得到9种桩端边界条件下基桩稳定计算长度与屈曲临界荷载。文献[6]基于桩土共同作用理论并计入桩身自重，得到基桩屈曲荷载与相应的计算长度。文献[7，8]对m法进行改进，提出将m法和常数法相结合的模型考虑桩侧土弹性抗力，并给出超长桩的临界荷载和计算长度系数。

值得注意的是，上述研究成果表明桩侧土抗力和桩身自重均会在某种程度上影响着超长桩的屈曲荷载。但现有的桩屈曲荷载计算理论能同时考虑以上两个影响因素的桩屈曲荷载计算公式目前文献还很鲜见。基于此，本文同时考虑桩侧土抗力和桩身自重的影响，应用瑞利-里兹法和最小势能原理给出桩屈曲荷载和计算长度的理论公式。最后着重分析了桩侧土抗力和桩身自重对屈曲荷载的影响。

1 力学计算模型及基本假定

图1为超长嵌岩桩屈曲稳定承载力的计算模型。桩身长度为L，入土深度为h；桩端部自由，底部固定支承；桩顶受轴向荷载P作用，当计入桩身自重时，桩身任意截面x处轴向力P(x)的表达式为

式中，γ为桩身混凝土重度；A为桩身截面积。

桩侧土体的弹性抗力计算模型为地基系数随深度呈抛物线变化，即吻合c值法。相应的地基反力q基于Winkler假设，即

式中，m地基土水平抗力系数；b1为桩的计算宽度。文献[10]指出，对于桩径为d圆形桩：当d≤1 m时，b1=0.9(1.5d+0.5)；当d＞1 m时，b1=0.9(d+1)；

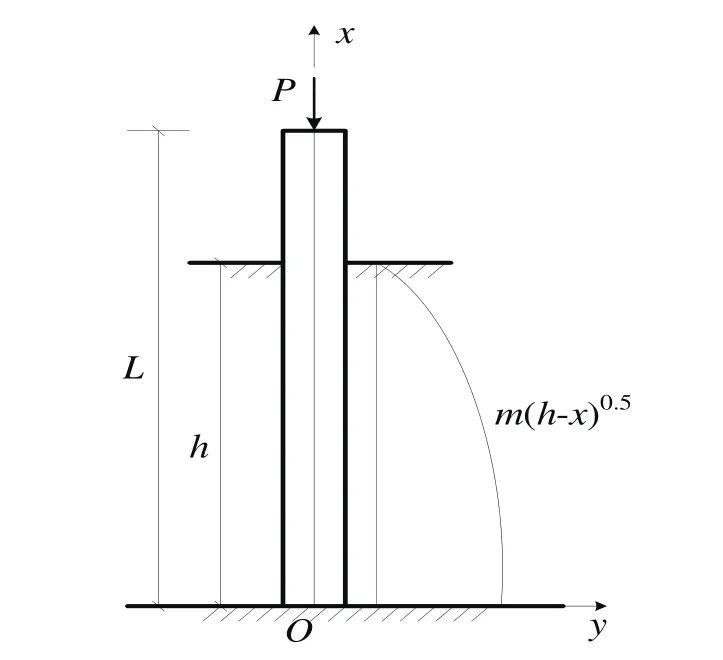
图1 桩屈曲临界荷载计算的力学模型

2 用瑞利-里兹法求解临界荷载

按照里兹法选取满足相应几何边界条件的超长桩挠曲变形函数为

式中，C待定的常数参量。

由式（3）得挠曲变形函数的一阶、二阶导数分别为

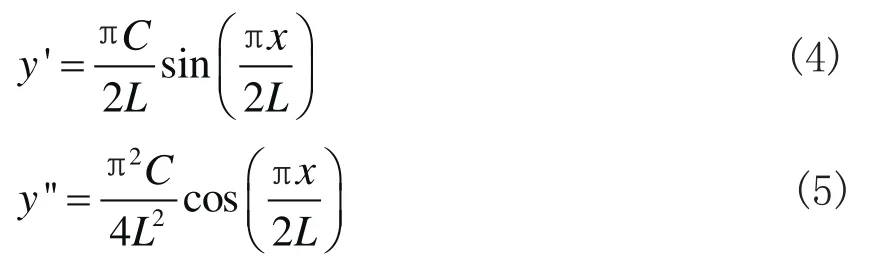
如图1所示的桩土系统在外荷载P作用下的总势能Π为

式中，U1为桩的弯曲应变能；U2为土体的弹性变形能；Vp为外荷载的势能。

桩的弯曲应变能U1可表达为

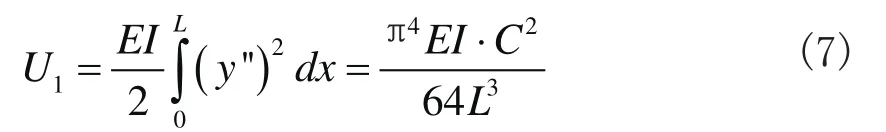
式中，E为桩身材料的弹性模量；I为桩身截面惯性矩。

同时，桩周土体的弹性变形能U2表达为

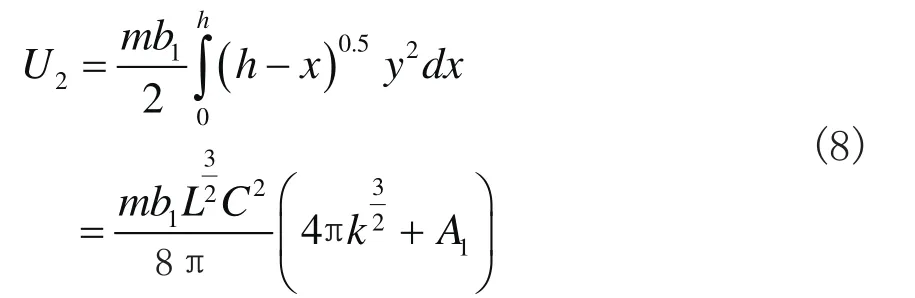
式中，m为桩侧土水平抗力系数；k为桩身埋置率，k=h/L；

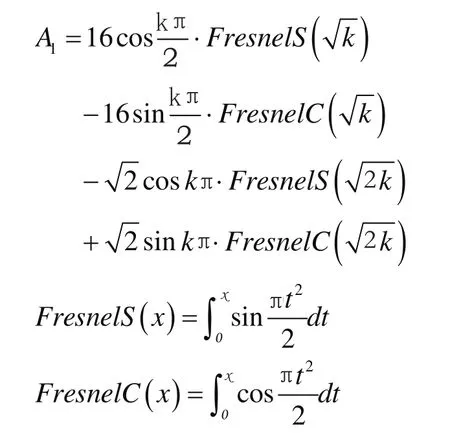
式（6）中外荷载势能VP的表达式为

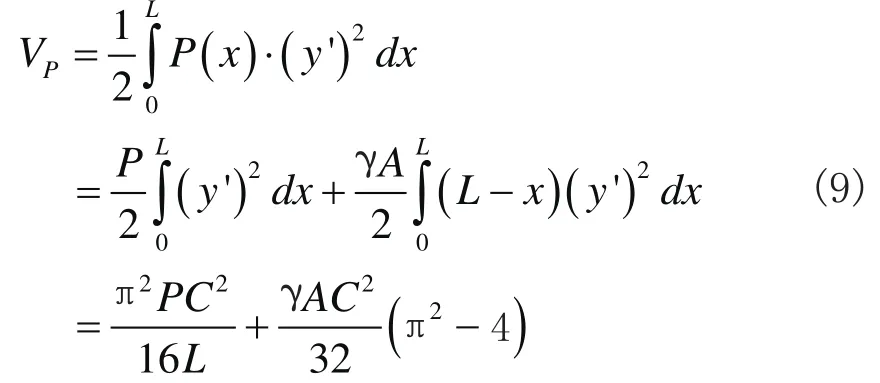
在此基础上，将式（7）、（8）、（9）代入式（6），可得到桩土体系的总势能的表达式为

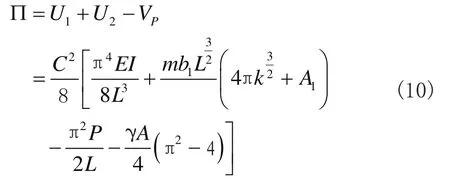
式中，A1与式（8）中相同。

由势能驻值原理有： ∂ Π / ∂ C = 0 ，即

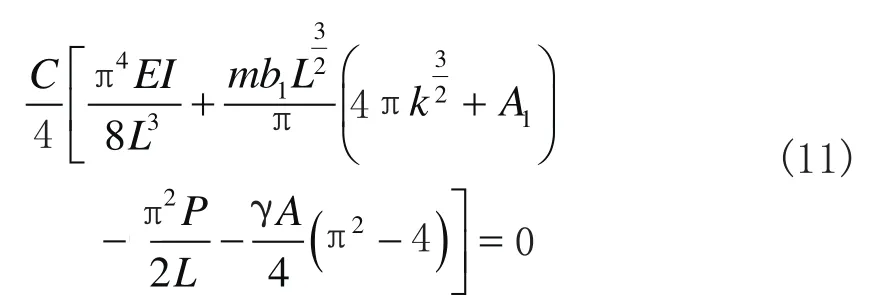
因C不能为零，故有

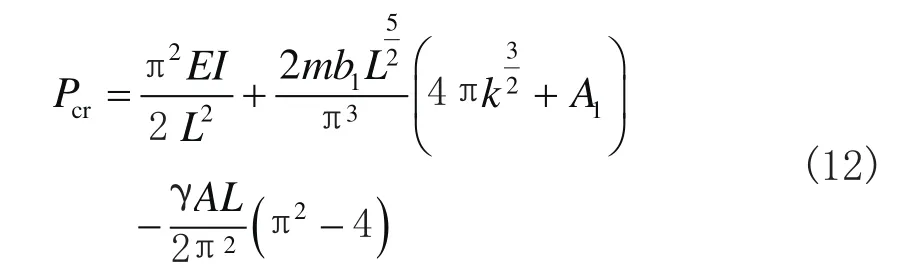
式中，A1与式（8）中相同。

式（12）即为所求的临界荷载计算公式。在获得桩临界荷载计算公式的基础上，可进一步求得桩计算长度系数为

由上述公式知，临界荷载Pcr除与桩身刚度EI，桩的计算宽度b1，桩的长度L，入土深度h，地基土比例系数m等因素有关外，还取决于桩身混凝土重度γ。

如果不考虑桩桩身自重时，上述公式（12）退化为文献[9]的解，即

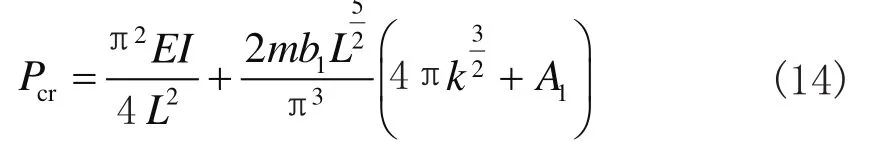
式中，A1与式（8）中相同。

当不考虑桩身自重且入土深度h=0时，即为无桩侧土弹性抗力、无桩侧摩阻力的普通压杆屈曲荷载计算公式，此时临界荷载Pcr的表达式为

式（15）即为一端固定支承、一端自由时普通压杆稳定的欧拉公式。这两点恰好说明本文得到的临界荷载的解析表达是十分可靠的，其解答均能退化为各种特殊情况下已获得的解析解。

以下将通过实例分析不同的入土深度时临界荷载的异同，并讨论桩身自重对超长桩稳定性的影响。

3 算例分析

某桩嵌于岩层内，桩身材料为C25混凝土，弹性模量Eh=2.85×104 MPa，桩长为60 m，桩底持力层为砂砾石，桩径为1.2 m，根据规范可得桩的计算宽度b1=0.9(d+1)=1.98 m，桩身截面面积A=1.13 m²，桩身的抗弯刚度为EI=0.85EhI=2.465×106kN.m²，覆盖层为淤泥质流塑性黏土，取地基土比例系数m=5000 kN/m4，钢筋混凝土桩身重度γ=25 kN/m³。利用欧拉公式可计算此条件下普通压杆稳定的临界荷载为1687.77 kN。

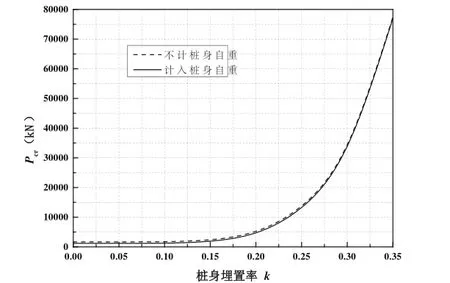
图2 考虑自重时临界荷载与桩身埋置率的关系

利用公式（12）和（14）可分别计算上述条件下考虑桩身自重和不考虑桩身自重时超长嵌岩桩的屈曲临界荷载。图2为考虑桩身自重时桩屈曲临界荷载与桩身埋置率的关系曲线。由图2可以看出，计入与不计桩身自重时临界荷载值均随桩身埋置率的增加而增加，即桩入土深度越大，临界荷载值越大。当桩身埋置率k＜0.15时，桩屈曲临界荷载值随桩身埋置率的增加而缓慢增加；当桩身埋置率k＞0.3时，桩屈曲临界荷载值随桩身埋置率的增加较快。考虑桩身自重时的桩屈曲临界荷载值比不计桩身自重时小。为更直观地说明该问题，计入与不计桩身自重时桩屈曲临界荷载值如表1所示。

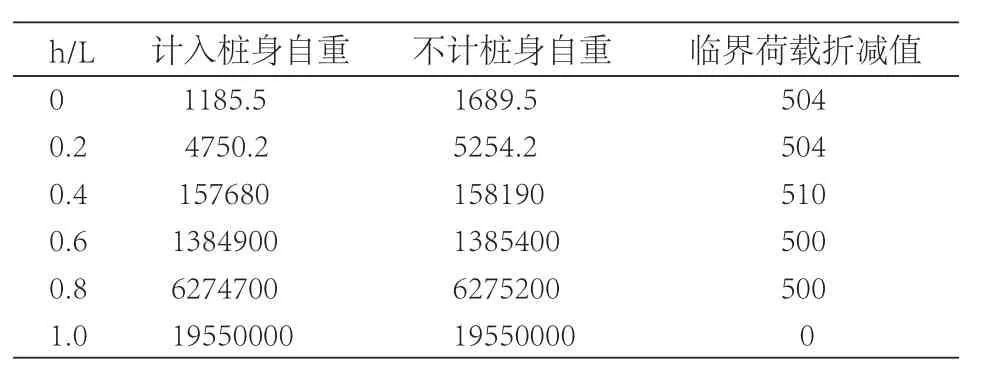
表1 计入与不计桩身自重时临界荷载比较

考虑桩身自重时桩屈曲临界荷载值的折减率与桩身埋置率的关系曲线如图3。由图可看出，当桩身埋置率较低（k≤0.4）时，超长桩屈曲临界荷载折减率较大，说明桩身自重对桩屈曲临界荷载值影响较大。当桩身埋置率k＞0.4时，曲线几乎为零，说明与桩侧土抗力相比，桩身自重对桩的屈曲荷载值的影响甚微。因此，对于埋置率较低的高承台桩基，计算屈曲荷载时应考虑自重对桩屈曲稳定的影响。

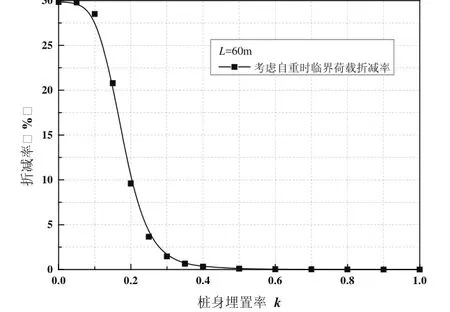
图3 考虑自重时临界荷载折减率与桩身埋置率的关系

4 结 论

针对目前沿海地区大型工程中使用的桩基长度大于50 m的情况比较普遍，而对这种超长桩承载能力的研究相对滞后的现状，本文同时考虑桩侧土抗力和桩身自重的影响，得到桩屈曲临界荷载和桩的计算长度系数的计算公式，并通过算例分析得到以下结论：

（1）桩身自重对超长桩屈曲临界荷载影响较大，特别是当桩入土深度小于桩长的40%时，不考虑桩身自重会导致临界荷载偏大，致使按桩身强度设计的承载力偏于不安全。因此对实际工程中埋置率较小的高承台桩计算桩身稳定时有必要考虑桩身自重的影响。

（2）综合分析桩侧土抗力模式和桩身自重两方面影响因素，结果表明，桩侧土抗力模式仍是影响临界荷载的最主要因素。

[1]Davisson M T, Robinson K E. Bending and buckling partially embedded piles[C]. Proceeding 6th International conference on Soil Mechanic and Foundation Engineering. Toronto: University of Toronto Press, 1965: 243-246.

[2]Toakley A R. Buckling loads for elastically supported struts[J].Journal of Engineering Mechanics and Foundation Divison,ASCE, 1970,96(6): 1951-1965.

[3]彭锡鼎.考虑桩侧土壤弹性抗力时桩的临界荷载计算[J]. 土木工程学报,1996,29(5): 43-48.

[4]赵明华.桥梁桩基稳定计算长度[J].工程力学,1987,4(1): 94-105.

[5]赵明华,王季柏.基桩计入摩阻力的屈曲分析[J].岩土工程学报,1996,18(3): 87-90.

[6]杨健,沈惠申,张乐.桥梁基桩的屈曲荷载计算.上海交通大学学报[J],2000,34(4): 533-537.

[7]王成,董倩. 超长桩稳定承载力计算新方法[J]. 岩土力学,2005,26(S): 180-182.

[8]刘礼标,王成.考虑桩侧双线性土抗力时长桩临界荷载计算[J].岩土力学,2007,28(S): 927-930.

[9]姚文娟,傅祥卿,仇元忠.超长桩的屈曲荷载计算[J]. 地下空间与工程学报, 2009, 5(3): 463-467.

[10]中国建筑科学研究院.建筑桩基技术规范:JGJ 94-2008[S]. 北京：中国建筑工业出版社,2008.

Buckling analysis for super-long pile considering self-weight of pile

TANG Wendong1, LIU Xiaozhao2

(1. Anhui Institute of Building Research & Design， Hefei ,Anhui 230001；2.Faculty of Civil Engineering and Mechanics, Jiangsu University, Zhenjiang, Jiangsu 212013)

Buckling analysis of super-long pile is an important subject. Due to the super-long pile’s large self-weight, the stability of the super-long pile has been greatly influenced. Most of the existing research only consider the influence of lateral resistance of soil on the buckling load, while the calculation of buckling load for long pile, with considering both factors of lateral resistance of soil and self-weight of pile has been rarely reported. In this paper, the influence of both factors have been taken into consideration. The analytical solutions for the buckling load and the calculation length of super-long pile are given by choosing the proper deflection function of pile, the elastic resistance model of lateral soil and the buckling load which is obtained with the method of Rayleigh-Ritz. Finally, this paper has analyzed the influences of lateral resistance of soil and the self-weight of pile on the buckling load and the calculation length of super-long pile. The result shows that the lateral resistance of soil mainly influences the buckling load. When the ratio of the depth to the length of pile (h/L) is at a low level, the influences of the self-weight of pile on the buckling load must be considered. With the increase in the value of this ratio, the influence of self-weight of pile gradually decreases to the yield load.

buckling analysis; super-long pile; buckling load; the method of Rayleigh-Ritz; self-weight of pile

TU473.11

A

2095-8382(2016)06-039-04

10.11921/j.issn.2095-8382.20160609

2016-04-05

唐文栋(1978-)，男，硕士，高级工程师，主要研究方向为地基基础及结构鉴定。