基于ARIMA模型的装备器材需求预测方法

刘旭阳， 吴龙涛， 周万里

(1. 装备学院研究生管理大队， 北京 101416； 2. 装甲兵工程学院技术保障工程系， 北京 100072； 3. 73668部队， 江苏 南京 211131)

基于ARIMA模型的装备器材需求预测方法

刘旭阳1,2， 吴龙涛2， 周万里3

(1. 装备学院研究生管理大队， 北京 101416； 2. 装甲兵工程学院技术保障工程系， 北京 100072； 3. 73668部队， 江苏 南京 211131)

分析了装备器材需求的影响因素，建立了装备器材需求时间序列的求和自回归移动平均(Auto Regressive Integrated Moving Average, ARIMA)模型，提出了基于ARIMA模型的装备器材需求预测方法，进行了实例分析，并与传统的预测方法进行了对比。结果表明:模型的预测精度明显优于传统的预测方法，且具有方差预测的优势。

装备器材； 需求预测； 求和自回归移动平均

随着装备训练任务量的增加、训练强度的增大，以及各种不确定性因素的增多，装备器材消耗规律更加复杂[1]。当前各级部门在拟制装备器材申请计划时，仍依据维修任务和消耗定额，采用定额计算法来确定装备器材需求量，各级仓库器材积压问题比较严重，而装备器材满足率却不尽如人意。

近年来，我军装备器材管理部门借助信息系统积累了大量的历史数据。因此，通过建模分析，寻求装备器材消耗规律并对其需求进行预测已成为可能。传统的移动平均法和指数平滑法[2]只能对趋势显著的序列进行确定性分析；灰色预测模型[3]虽能很好地解决小样本预测问题，但对于波动性较大的数列，其预测精度仍然不是很高；Croston法[4]和Bootstrap法[5]为间断性需求预测最常采用的方法，但预测效果不稳定；基于因素分析的预测方法大多采用回归分析[6]、人工神经网络[7]和支持向量机[8]等方法，从训练样本中提取各因素与需求量的关系，其预测准确性依赖于样本的容量和质量；基于可靠性的预测方法首先需要根据失效机理假设装备器材服从不同的寿命分布[9]，然后再依据假设建立装备器材配置模型，该方法忽略了可靠性之外的其他因素对装备器材需求的影响，且若假设有误，则误差很大。

装备器材需求时间序列是各种确定性因素和随机因素综合作用的结果，对这种时间序列进行统计分析并建立量化模型[10]，可发掘其中蕴含的有效信息。求和自回归移动平均 (Auto Regressive Integrated Moving Average, ARIMA) 模型是一种重要的时序分析方法，模型拟合和短期预测精度高，在经济、金融等领域已得到了广泛应用[11-13]。为此，笔者对装备器材需求影响因素进行分析，建立装备器材需求时间序列的ARIMA模型，并应用该模型对某装甲旅仓库的维修器材需求进行预测，验证该模型的有效性。

1 装备器材需求影响因素分析

装备器材需求与装备动用、维修活动密切相关，需求的变化受多方面因素的影响，其中既有确定性因素，如装备动用、装备维修等，又有随机性因素，如环境气候、人员素质等。

装备动用时间和强度是影响装备器材需求的重要因素，由于不同季节的训练强度和内容不同，使装备器材需求具有季节性；同时，随着演习等任务的增加、训练强度的增大，近年来装备器材需求量呈现增大的趋势。装备器材的可靠性、装备动用环境、气候以及使用人员素质等则具有更多的不确定性，进而使装备器材需求出现随机波动。

装备器材需求是上述各因素综合作用的结果，基于因素分析的预测方法或基于可靠性的预测方法很难对装备器材需求进行全面准确的预测。因此，笔者从时序分析的角度，利用ARIMA模型的优势建立装备器材需求预测模型。

2 ARIMA模型构建

ARIMA模型的实质是差分运算与自回归移动平均 (Auto Regressive Moving Average, ARMA) 模型的结合，通过适当阶数或步数的差分实现非平稳序列的平稳化，然后对差分后序列拟合ARMA模型。图1为ARIMA模型的构建流程。

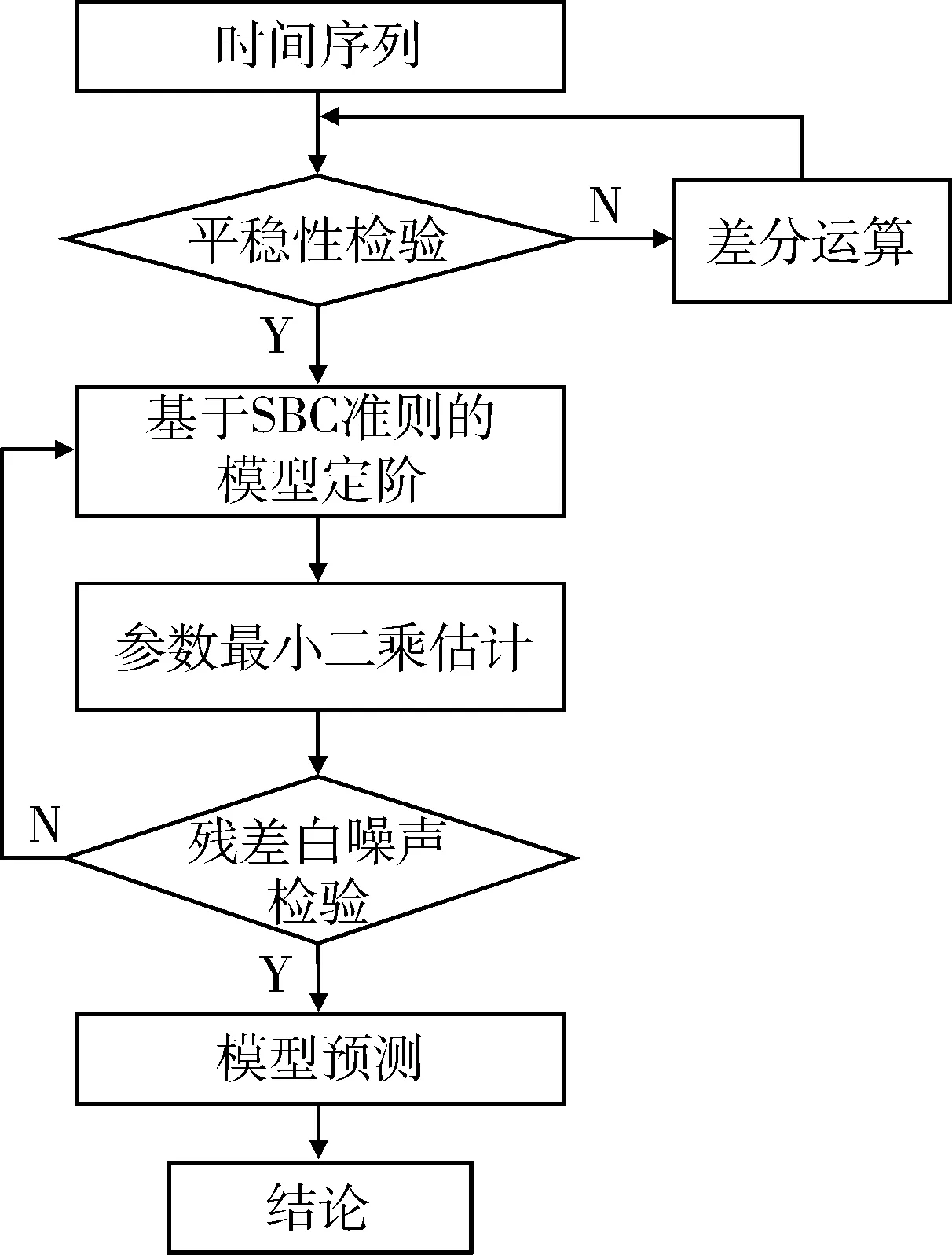
图1 ARIMA模型构建流程

2.1 时间序列平稳性检验及处理

平稳时间序列具有常数均值和方差等统计特性，对于非平稳序列，需经过变换处理后才能构建拟合模型。图检验法根据时序图、自相关系数和偏自相关系数图的特征进行平稳性判别，操作简单，是常用的平稳性检验方法[10]。

差分运算可充分地提取非平稳序列中的趋势性和周期性等信息，是一种有效的平稳化处理方法。对于显著的线性或曲线趋势，可进行低阶差分运算；而步长为周期长度的差分运算，可较好地提取周期信息。差分阶数d可根据观测序列时序图的趋势和季节效应决定，以通过平稳性检验为准。

2.2 ARIMA模型定阶和参数估计

中心化ARIMA(p,d,q)模型结构为

(1)

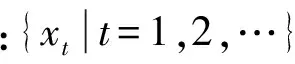
(2)

式中：Φ(B)和Θ(B)分别为自回归和滑动平均系数多项式。

对于p和q的定阶问题，传统的图定阶法主观性强且不精确。崔建国等[13]利用遗传算法进行定阶，但该方法过度追求拟合精度，确定的p和q值过大，不利于参数估计，因为拟合精度越高，模型参数就越多；而参数越多，参数估计的难度就越大,精度就越低。SBC(Schwartz Bayes Criterion)准则[10]应用似然函数衡量拟合精度，并从拟合精度和参数个数2个角度来评价拟合模型，即S=-2ln(极大似然函数值)+ln(n)(参数个数)。为此，笔者引入SBC准则，并在一定范围内遍历p和q值，当S值最小时，即为实现拟合精度和参数个数之间最佳平衡的相对最优模型。对于中心化ARIMA(p,d,q)模型，其对数似然函数满足条件

(3)

又因为模型参数个数为p+q+1，所以模型的SBC函数值为

(4)

对于p+q+1个未知参数的估计，常用的矩估计法比较粗糙，精度不高；极大似然估计精度较高，但必须已知装备器材需求的总体分布函数。由于条件最小二乘估计法不需要已知装备器材需求的总体分布函数，且估计精度较高，因而笔者采用该方法进行参数估计。

2.3 残差序列的白噪声检验

理想拟合模型的残差序列应为白噪声序列，不含任何相关性信息。因此，需对残差序列进行白噪声检验。首先计算样本的自相关系数

(5)

式中：k=1,2,…,n-1，其中n为序列长度。

然后构造LB统计量进行白噪声检验，即

(6)

2.4 基于ARIMA模型的装备器材需求预测

(7)

式中：

最小预测方差为

(8)

(9)

3 实例分析

某装甲旅维修器材仓库负责保障该旅装甲装备小修、检修、维护保养以及伴随保障等所需的维修器材。装备动用情况为影响该仓库器材需求的主要因素，装备训练多集中在夏、秋季节，维修任务相对集中，因而器材需求较冬、春季节偏多。以仓库中S器材2011-2014年逐月的需求数据为例，采用笔者提出的器材需求时序模型进行拟合分析和预测。

3.1 装备器材需求时间序列的平稳性检验及差分处理

图2为S器材需求观测序列时序图。可以看出：S器材的月消耗观测序列具有明显的线性递增趋势，且以1年为周期进行波动，是典型的非平稳序列。

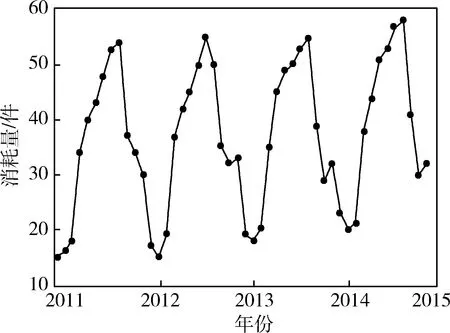
图2 S器材需求观测序列时序图

通过差分运算对序列进行平稳化处理，依次进行1阶趋势差分和12步周期差分运算。图3为S器材需求差分序列相关分析。可以看出：器材需求时间序列没有明显趋势或周期，自相关系数相关性表明序列具有2阶短期相关性，因此差分后序列基本平稳。

3.2 模型定阶和参数估计

由图3可以看出：自相关系数和偏自相关系数均具有2阶截尾性，因此在0≤p≤2和0≤q≤2范围内，依据SBC值最小准则确定模型阶数，结果如表1所示。选择ARMA(0,2)模型对S器材差分后需求序列进行拟合。

应用条件最小二乘估计法对未知参数进行估计，可得拟合模型为

(10)

进一步变换处理可得

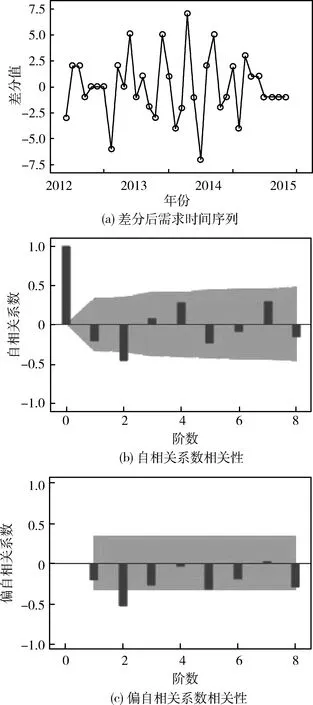
图3 S器材需求差分序列相关分析

表1 基于SBC准则的模型定阶

xt=xt-1+xt-12-xt-13+εt-

0.597εt-1-0.381εt-2。

(11)

式中：xt为t时期S器材需求观测值；白噪声序列εt～N (0,2.3192) 。

3.3 残差序列的白噪声检验

为拟合模型的残差序列构造LB统计量，应用SAE统计分析软件进行残差的白噪声检验，结果如表2所示，可以看出：延迟各阶的LB统计量的P值均显著大于α (α=0.05)，表明所构建的ARIMA拟合模型有效。

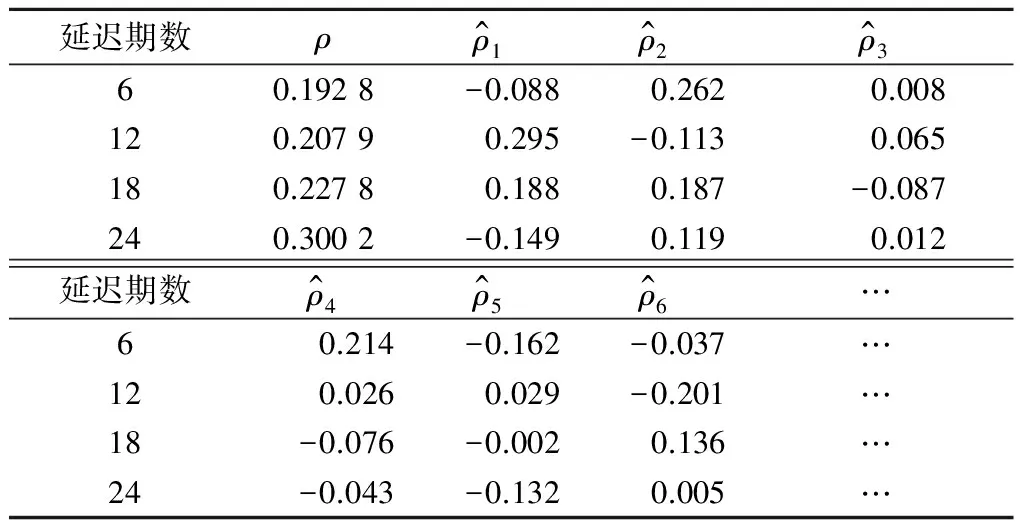
表2 残差的白噪声检验

3.4 预测结果对比分析

基于S器材2011-2014年的需求数据，分别利用移动平均法、指数平滑法 (平滑系数为0.5)、灰色GM (1,1)模型和笔者提出的ARIMA拟合模型对S器材2015年各月的需求量进行预测，并与实际需求量进行对比，结果如图4所示。

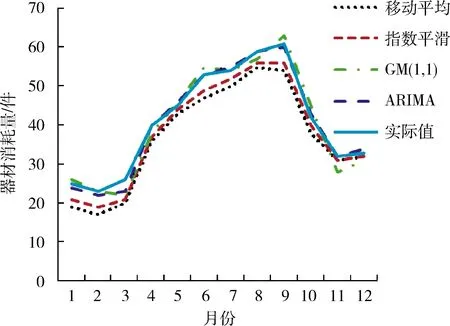
图4 S器材2015年各月的需求预测结果对比

4种方法预测值的平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)和年度需求量预测误差对比结果如表3所示。其中：MAPE的计算公式[14]为

(12)

表3 4种方法预测结果的误差对比

由图4和表3可以看出：基于ARIMA模型的预测效果最佳，其次为灰色GM (1,1) 模型，而指数平滑法和移动平均法的预测准确性相对较差。这是因为：灰色GM (1,1) 模型、指数平滑法和移动平均法只能对时间序列中的趋势性进行预测；而ARIMA模型对时间序列中的趋势性和季节性都能很好地进行预测。

ARIMA模型除了对需求均值进行预测外，还可预测需求方差，从而便于计算器材需求的概率分布函数和后续库存控制建模。如在各月需求相互独立的假设下， 根据式 (8)，可得2015年度装备器材需求的预测方差为74.278。

4 结论

装备器材需求发生过程受各种确定性因素和随机因素的影响，传统的预测方法很难进行全面、准确的预测。当前利用ARIMA模型进行需求预测的研究并不多见，笔者提出了基于ARIMA模型的装备器材预测方法，可很好地对经常性消耗器材进行需求预测。但在研究过程中也发现：对于某些需求波动特别大的装备器材，该方法预测效果并不理想。其原因主要是这些器材需求时间序列的残差序列具有异方差性。下一步，将针对这一特性进行深入研究。

[1] 蔡丽影,毛丰超,王凯,等.美陆军两级维修体制改革及启示[J].装备学院学报,2014,25(5):40-44.

[2] 齐驰,侯忠生.自适应单指数平滑法在短期交通流预测中的应用[J].控制理论与应用,2012,29(4):465-469.

[3] 郭晓君,刘思峰,吴利丰.污染物减排预测的灰色Markov组合模型与算法[J].计算机应用研究,2013,20(12):3670-3673.

[4] Snyder R D,Ord J K,Beaumont A.Forecasting the Intermittent Demand for Slow-moving Inventories:A Modeling Approach [J].International Journal of Forecasting,2012,28(6):485-496.

[5] Willemain T R,Smart C N,Schwarz H F.A New Approach to Forecasting Intermittent Demand for Service Parts Inventories [J].International Journal of Forecasting,2004,20(1):375-387.

[6] 牛京考.基于主成分回归分析法预测中国铁矿石需求[J].北京科技大学学报,2011,33(10):1177-1181.

[7] Venkatesh K,Ravi V,Prinzie A.Cash Demand Forecasting in ATMs by Clustering and Neural Networks [J].European Journal of Operational Research,2014,232(3):383-392.

[8] Carbonneau R,Laframboise K,Vahidov R.Application of Machine Learning Techniques for Supply Chain Demand Forecasting [J].European Journal of Operational Research,2008,184(5):1140-1154.

[9] Kamath K R,Pakkala T P M.A Bayesian Approach to a Dynamic Inventory Model under an Unknown Demand Distribution [J].Computers and Operations Research,2002,29(1):403-422.

[10] 王燕.应用时间序列分析[M].2版.北京:中国人民大学出版社,2012：148-156.

[11] Arunraj N S,Ahrens D.A Hybrid Seasonal Autoregressive Integrated Moving Average and Quantile Regression for Daily Food Sales Forecasting [J].International Journal of Production Economics,2015,170(4):321-335.

[12] Lee Y S,Tong L I.Forecasting Time Series Using a Methodology Based on Autoregressive Integrated Moving Average and Genetic Programming [J].Knowledge-based Systems,2011,24(1):66-72.

[13] 崔建国,赵云龙,董世良,等.基于遗传算法和ARMA模型的航空发动机寿命预测[J].航空学报,2011,32(8):1506-1511.

[14] Syntetos A A,Boylan J E.The Accuracy of Intermittent Demand Estimates [J].International Journal of Forecasting,2005,21(2):303-314.

(责任编辑: 王生凤)

Equipment Material Demand Forecasting Method Based on ARIMA Model

LIU Xu-yang1,2, WU Long-tao2, ZHOU Wan-li3

(1. Brigade of Postgraduate Management, Equipment Academy, Beijing 101416, China; 2. Department of Technical Support Engineering, Academy of Armored Force Engineering, Beijing 100072, China; 3. Troop No.73668 of PLA, Nanjing 211131, China))

The factors affecting the equipment material demand are analyzed, and an Auto Regressive Integrated Moving Average (ARIMA) model of equipment material demand time series is built. A forecasting method of equipment material demand based on ARIMA model is presented, the example is analyzed and compared with the traditional prediction methods. The results show that the proposed model performs better than the traditional methods in forecasting accuracy, and has the advantage of variance forecasting.

equipment materials; demand forecasting; ARIMA

2016-10-18

军队科研计划项目

刘旭阳(1978-)，男，讲师，博士研究生。

E92

：ADOI：10.3969/j.issn.1672-1497.2016.06.005

1672-1497(2016)06-0021-05