多维超几何分布的概率计算问题研究

李玉萍, 张金诺

(1.郑州师范学院 数学与统计学院,郑州 450044; 2.中国地质大学 经济与管理学院,武汉 430074)

多维超几何分布的概率计算问题研究

李玉萍1, 张金诺2

(1.郑州师范学院 数学与统计学院,郑州 450044; 2.中国地质大学 经济与管理学院,武汉 430074)

把超几何分布进行了推广，引出多维超几何分布的定义,给出了多维超几何分布最可能成功数.并在此基础上,探讨了多维超几何分布、多项分布和多维Poission分布之间的极限分布,从而可以解决超几何分布的概率计算问题.

超几何分布;最可能成功数;多项分布;多维Poission分布

超几何分布是产品计数抽样检验和可靠性问题中经常遇到的一类重要的概率模型.但是在实际的抽样调查中，还经常遇到定性的问题，例如总体的N个个体中，总体包含A1,A2,…,Ar共r类属性.此时被研究的对象就推广为3种或3种以上，于是我们就需要对超几何分布进一步推广，引申出多维超几何分布.文献[1]用概率母函数求出了超几何分布的期望和方差，文献[2]给出了超几何分布概率的递推算法，文献[3]给出了超几何分布数字特征的定义求法，文献[4]给出了超几何分布高阶矩的简便求法，文献[5]对超几何分布的概率计算进行了探讨，文献[6]对超几何分布的定义进行了推广，文献[7]对多维超几何分布的协方差矩阵进行了简单求解，文献[8]把多维超几何分布的最可能成功数推广到三维，文献[9]给出了3种分布之间的极限关系.本文把多维超几何分布的最可能成功数推广到多维并且进一步探讨了多维超几何分布、多项分布和多维Poisson分布的极限分布关系，从而可以有效地解决多维超几何分布的概率计算问题.

1 超几何分布的推广

设随机变量X的分布率为

(k=b,b+1,…,d.其中b=max(0,n+M-N),d=min(n,M))

于是称随机变量X服从超几何分布X～H(n,N,M).参数为n,N,M.

作为超几何分布的引申推广，我们如果将研究对象由两种情况推广为3种或3种以上，就得到了多维超几何分布.

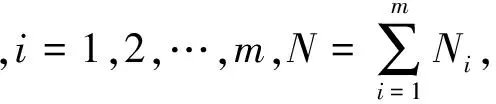
其中(0≤ni≤Ni(i=1,2,…,m),0≤ni≤N).

此时，称随机向量(X1,X2,…,Xn)服从m维超几何分布H(k1,k2,…,km).

特殊地，若随机向量的联合分布为

其中0≤h≤N1,0≤i≤N,0≤n≤N，,这时称随机向量服从三维超几何分布.那么它可以表述为：袋中有产品N个，其中一等品和二等品分别为N1，N2个，其他为次品，从中不放回地任取n个，X1与X2表示一等品和二等品的件数.

2 超几何分布最可能成功数的推广

(1)当x=m=[(M+1)(n+1)/(N+2)]≠(M+1)(n+1)/(N+2)时，m为P(x=m)的最可能成功数.

(2)当x=m=[(M+1)(n+1)/(N+2)]=(M+1)(n+1)/(N+2)时，m，m-1都为P(x=m)的最可能成功数.

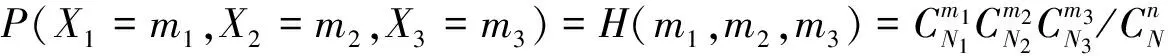
当m1=[(N1+1)(n+1)/(N+2)]且m2=[(N2+1)(n+1)/(N+2)]时，H(m1,m2,m3)取得最大值，同时：

(1)当m1=[(N1+1)(n+1)/(N+2)]≠(N1+1)(n+1)/(N+2)，m2=[(N2+1)(n+1)/(N+2)]=(N2+1)(n+1)/(N+2)，m3=(N3+1)(n+1)/(N+2)-1时，H(m1,m2,m3)与H(m1,m2-1,m3+1)都取得最大值.

(2)当m1=[(N1+1)(n+1)/(N+2)]=(N1+1)(n+1)/(N+2)，m2=[(N2+1)(n+1)/(N+2)]≠(N2+1)(n+1)/(N+2)，m3=(N3+1)(n+1)/(N+2)-1时，H(m1,m2,m3)与H(m1,m2-1,m3+1)均为最大.

(3)当m1=[(N1+1)(n+1)/(N+2)]=(N1+1)(n+1)/(N+2)，m2=[(N2+1)(n+1)/(N+2)]=(N2+1)(n+1)/(N+2)，m3=(N3+1)(n+1)/(N+2)-1时，H(m1,m2,m3)，H(m1-1,m2,m3+1)，H(m1,m2-1,m3+1)均取得最大值.

于是可以推广得到

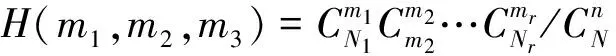
(1)当mi=[(Ni+1)(n+1)/(N+2)]≠(Ni+1)(n+1)/(N+2)时，xi=mi(i=1,2,…,r-1)使得H(m1,m2,m3)取得最大值.

(2)当mi=[(Ni+1)(n+1)/(N+2)]=(Ni+1)(n+1)/(N+2)时，且mr=(Nr+1)(n+1)/(N+2)-1时，H(m1或m1-1,m2,…,mr-1-1,mr+1),H(m1,m2或m2-1,…,mr-1,mr+1),…,H(m1,m3,…,mr-1或mr-1-1,mr+1)都是最大值.

(3)当xi(i=1,2,…,r-1)中有b个xi对于[(Ni+1)(n+1)/(N+2)]≠(Ni+1)(n+1)/(N+2)成立，而另外d个xi对于[(Ni+1)(n+1)/(N+2)]=(Ni+1)(n+1)/(N+2)成立，b+d=r-1，且mr=(Nr+1)(n+1)/(N+2)-1时，

上述b个xi相应地取值为xi=mi，d个xi取值为xi=mi或者xi=mi-1,同时当mr=(Nr+1)(n+1)/(N+2)-1时，得H(x1,x2,x3)达到最大值.

3 多维超几何分布的极限分布及概率计算

3.1 r维超几何分布趋向于r项分布

服从(n,p1,p2,…,pr)的r项分布表述了这样的一种概率模型：在n次独立重复试验中(注：放回有序抽样)，试验结果具有特征(A1,A2,…,Ar)，个数分别为(m1,m2,…,mr)，这里P(Ai)=pi,i=1,2,…,r.

同时r维超几何分布与r项分布之间联系密切.多维超几何分布源于不放回抽样，多项分布源于放回抽样.所以当总体中元素的数量N很大，抽样的次数n相对很小时，不放回抽样可以近似等同放回抽样.因此,可以认为r维超几何分布的极限分布是r项分布.即有：

定理2假定r维超几何分布中参数Ni满足条件

则r维超几何分布的极限分布可认为是r项分布.对于任意自然数n和给定的满足mi=0,1,…,n,m1+m2+…+mr=n的m1,m2,…,mr,有

当N→∞时，也有Ni→∞,i=1,2,…,r,那么在上式中令N→∞时，定理中的结论得以证明.

3.2 r项分布近似于r-1维的Poisson分布

定义2假定λ1,λ2,…,λr是r个正实数，如果r维随机向量(X1,X2,…,Xr)取值(m1,m2,…,mr)的概率为

r维Poisson分布描述了这样的一种分布，随机试验结果具有特征(A1,A2,…,Ar)，个数为(m1,m2,…,mr)，而其中每一个特征Ai出现的个数，有可能为一切非负的整数.

定理3在r项分布中，如果以pn,i代替pi(n次独立重复试验中，试验结果具有特征Ai的概率为：P(Ai)=pn,i)，假定pn,i满足

必有r项分布的极限服从于r-1维的Poisson分布，即对于给定的

mi=0,1,2,…；i=1,2,…,r-1(mr=n-(m1+m2+…+mr-1))，都有

证明若记λn,j=npn,j,则有

同时，n→∞时，对于任意的定值m1，m2，…，mr-1，

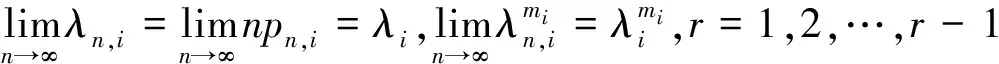
而且

定理3得证.

[1] 马松林.超几何分布的数学期望和方差的一种新求法[J].巢湖学院学报，2006,8(3)：139-140.

[2] 唐守宪.超几何分布的递推算法[J].辽宁师范大学学报，2004,2(3):13-14.

[3] 匡能辉.超几何分布的数学期望和方差的定义求法[J].高等数学研究，2010,4(3):15-16.

[4] 李金秋，田秋菊.超几何分布高阶矩的一种简便算法[J].科学技术与工程，2010,32(3):39-40.

[5] 李玉萍，刘心馨.超几何分布的数字特征和概率计算的探讨[J].大学数学，2015,31(3):102-105.

[6] 燕建梁.超几何分布及其推广[J].太原师范学院学报，2013,12(1):21-23.

[7] 吕宏啸.多维超几何分布协方差矩阵的简单求法[J].佳木斯大学学报，2012,30(6):944-945.

[8] 孟雪，宋立新.多维超几何分布的最可能成功数[J].佳木斯大学学报，2010,28(4):590-592.

[9] 戴朝寿，姚承轩.多维超几何分布、多项分布与多维Poisson分布之间的关系[J].徐州师范学院学报，1994,12(2):12-15.

[责任编辑 王新奇]

Study on the Problem of Probability Calculation ofMultidimensional Hyper Geometric Distribution

LI Yu-ping1, ZHANG Jin-nuo2

(1. School of Mathematics and Statistics, Zhengzhou Normal University, Zhengzhou 450044, China;2. School of Economics and Management, China University of Geosciences, Wuhan 430074, China)

In this paper, the hyper geometric distribution is generalized, and the definition of multidimensional hyper geometric distribution is drawn out, and the most probable success number of multidimensional hyper geometric distribution is given. And on the basis of this, the limit distribution of multidimensional hyper geometric distribution, multinomial distribution and multidimensional Poission distribution are discussed, which can solve the problem of the probability calculation of the hyper geometric distribution.

hyper geometric distribution; the most probable success number; multinomial distribution; multidimensional Poission distribution

1008-5564(2016)05-0012-04

2016-03-16

河南省教育厅重点项目(2016-JSJYZD-072)；河南省科技厅软科学计划项目(132400410697)

李玉萍(1971—),女，河南郑州人，郑州师范学院数学与统计学院副教授，硕士，主要从事概率分布论研究.

O212

A