锂离子电池无机固体电解质的计算*
2016-02-10高健何冰施思齐
高健,何冰,施思齐③†
①上海大学材料基因组工程研究院,上海 200444;②上海大学计算机工程与科学学院,上海 200444;③上海大学材料科学与工程学院,上海 200444
锂离子电池无机固体电解质的计算*
高健①,何冰②,施思齐①③†
①上海大学材料基因组工程研究院,上海 200444;②上海大学计算机工程与科学学院,上海 200444;③上海大学材料科学与工程学院,上海 200444
利用高通量计算来挖掘材料基因是加速材料研发的有效手段。利用第一性原理对目标材料进行精确计算,可以得到晶体结构、电子结构、缺陷、相图与相变、离子/电子输运机制等信息。通过综述锂离子电池无机固体电解质材料的计算研究进展,展望了计算在高电导率、宽电化学窗口且与正负极匹配的固体电解质材料的高效优化、选取和设计方面的应用前景。
锂离子电池;无机固体电解质;材料基因工程;高通量计算;第一性原理计算
石油资源短缺和环境问题紧迫使“绿色环保”成为人们日益关注的焦点。绿色环保的核心是“新能源”,新能源的核心是化学电源。二次锂(离子)电池因比容量大,储存和循环寿命长,无记忆效应,环境污染小,而被广泛应用于便携电器,如移动电话、笔记本电脑、摄像设备等,从而大力推动了信息产业化。近来智能电网的储能电源、混合动力车和电动车电源等能量型和功率型储能电源对其安全性问题提出了新的挑战,而电解质材料常常是引起安全问题的关键。
目前商业化的锂离子电池均采用可燃的有机电解液,即将锂盐溶于有机溶液中,并包含添加剂;凝胶电解质是将盐和溶剂同时溶于高分子聚合物形成的胶体状态电解质。电池充放电时内部升温较容易引起气体膨胀,从而导致封装材料破裂、漏液、起火,甚至爆炸。除安全隐患外,电解液的不可逆反应可以消耗电极中的活性Li,降低电池的循环容量;副反应产物可能增加电阻,影响充放电功率。此外,此类电池不易小型化,不适当的回收利用可能污染环境。
由于对安全性的需求引起对于更多电解质种类的关注。固态聚合物电解质将锂盐与聚合物复合,可应用于柔性可弯折电池。因其没有自由液体电解质,从而避免了漏液,而且电极、电解质和隔膜式一体结构使电池更耐冲击、振动、变形,大大缓解了燃烧、爆炸等安全问题。然而其电导率目前仍难以满足应用需求。熔盐电解质可以根据电池的需求来选择/设计合适的阳离子-阴离子组合,使得其电导率在工作温度范围内满足需求。其电化学窗口较宽,具有较好的高温性能,且具备不挥发、不易燃、不易爆、毒性小、熔点低等特点。但是,由于其成本较高,黏度较大,合成条件苛刻,且对环境中水分敏感,还需做进一步的研究。
无机陶瓷是另一种有竞争力的备选电解质材料,其具有不可燃烧、不会爆炸、无泄漏、不腐蚀等特点,是安全问题的根本解决方案。目前已研发出多种锂离子电导率可以与液体电解质相比拟的材料体系。由于固体电解质的锂离子迁移率接近1,因此当其与液体电解质总电导率相近时,前者的有效锂离子电导率要高得多。固体电解质具有的优点还包括:在较宽的温度范围内具有良好的离子传导性能及电化学稳定性,可以应用于严苛的极端环境,对国防安全有重大意义;较高的致密度和机械强度,可以抑制锂枝晶刺穿造成的短路,使得Li负极成为可能,并显著提高电池的能量密度。对于无机固体电解质的要求包括高的离子电导率、可忽略的电子电导、宽的电化学窗口,以及与电极材料匹配,包括较低的界面阻抗、不发生(电)化学反应、脱嵌锂/热膨胀过程中保持应力/应变匹配等。目前尚未有单种材料可以满足需求。丰富的锂离子无机晶体种类,既具有巨大的挖掘空间,也为选择合适的材料提出极大的挑战。由于无机固体电解质具有周期性的晶体结构,其性质易于计算,以材料基因组思想为基础将计算、数据库与实验结合,可以大大减小材料的开发周期和研发成本。本文将从材料的高通量筛选和精确计算两个角度,综述锂离子无机固体电解质的研究进展。
1 锂(离子)电池无机固体电解质高通量计算进展
2011年,美国总统奥巴马提出“先进制造业伙伴关系”计划,明确再工业化战略以期实现制造业的复兴。2011年底推出的“材料基因组计划”作为其重要部分,寻找和建立材料从原子排列到相的形成到显微组织的形成到材料性能与使用寿命之间的相互关系,期望大大加快材料研发速度,降低材料研发的成本,提高材料设计的成功率,为产品和设备提供新材料,并带动现今制造业的发展。2011年12月21—23日,以“材料科学系统工程”为主题的香山会议在北京举行,将锂离子电池材料作为代表性示范材料之一,计划将基于计算模拟的材料数据库、开源软件工具以及机器学习方法应用于锂(离子)电池的研发的全产业链,系统地提高能量密度,降低成本,提高服役寿命,并大大缩短锂(离子)电池产业链的研发周期。
Ceder教授是材料基因组计划的发起者之一,原就职于麻省理工大学,现就职于加州大学伯克利分校。他的研究组开发机器学习方法预测新结构[1]和挖掘现有数据库中缺失的材料[2-3],在已有数据库基础上建立新的数据库,并对其中的材料进行第一性原理计算[4-5]。目前已完成开源交互式可视化平台的建设,并期望将材料的设计、计算、证实、发布和分析测试结合起来,以提高材料开发速度[6]。Wang等[7]从氧离子堆积方式与锂离子通道的角度,提出氧的体心立方堆积,预示了高电导率的可能性。考虑到固体电解质与电极材料的界面电阻常常是全电池电阻的重要来源,Richards等[8]大量预测不同电解质/包覆层/电极材料之间的稳定性,以及化学反应可能形成的界面相产物,并计算界面相的离子电导率,以预测高性能的组合。此外,Ceder目前在各个学校工作的学生,依然为全固态电池高通量计算做出了大量相关的工作。马里兰大学的Mo等[9-10]从电化学窗口的角度,对固体电解质材料相对于正/负极的电化学稳定性进行了高通量计算。在全固态电池的服役过程中,固体电解质的力学性能同样重要。加州大学圣地亚哥分校的Ong等[11]计算了碱金属超离子导体的弹性性质。考虑到无机快离子导体除了可以作为固体电解质材料替代有机电解液,同样也可以作为水系电池的隔膜材料,Ong等[12]利用第一性原理计算了锂离子和钠离子超离子导体在不同电势以及酸碱性条件下相对于水系电解液的稳定性,并作出Pourbaix图,同时指出氧化物材料的稳定性通常优于硫化物/卤化物材料,碱金属类型同样会影响材料相对于环境的稳定性。
具有高的锂离子电导率是无机固体电解质材料的首要要求,而连通的锂离子通道是高电导率的先决条件。对于实验手段而言,锂离子通道可以通过中子衍射直接得到[13-14]。对于理论研究而言,可以通过基于能量变化的第一性原理[15-18],基于配位环境变化的键价方法(bond valence method, BVM)[17-21],以及基于几何结构的Voroni-Dirichlet分割[22]、Colony表面[23]、Procrystal分析[24]等方法计算获得。其中,键价理论一直以来广泛应用于晶体学中,可确定晶体结构里面原子的占据位置[25]。对于小体积的离子,如Ag+或者Li+,所有的原子可占据位点可能相互连通,形成一个原子价地图(valence map)。González-Platas等[26]编写VALMAP 程序,首次展示了该地图。新加坡国立大学(National University of Singapore, NUS)的Adams小组[27-28]基于BVM开发了新程序,可以获得三维的原子价态图,即“离子通道”。BVM最大的优势在于“快速”和“可视化”,使得高通量计算并筛选固体电解质成为可能[27,29]。此外,他们在理论方面做出的努力,包括使该计算方法更适合于计算载流子的离子通道[29-32],以及赋予计算结果能量尺度(类似于跃迁势垒)的意义[33-34]。得益于这种方法的低计算成本,该组已完成对于无机晶体结构数据库(Inorganic Crystal Structure Database, ICSD)中碱土金属离子材料中锂离子通道的计算和材料的筛选[35]。此外,该组与Aarhus大学合作,利用Procrystal方法可视化锂离子迁移通道。该方法基于原子的球壳状电子密度,同样具有计算快速的特点,并应用在电池材料的筛选中[24]。
中国科学院物理研究所陈立泉院士是中国“材料科学系统工程”香山会议的发起人之一,目前其课题组从国际衍射数据中心(International Centre for Diffraction Data, ICDD) 数据库中获得材料的结构数据,从中提取含锂、无重金属、无变价元素的材料作为备选数据库利用BVM计算其离子通道。筛选过程如图1所示[36],将锂离子通道连通的材料作为固体电解质候选材料,并对目标材料进行第一性原理计算研究[37]。该课题组采用改进的方法,将键价参数用Morse势与静电库仑势表示,得到使离子通道连通的活化能,与密度泛函理论(density functional theory, DFT)计算值比较如图2所示[38]。2015年4月23日,由上海大学牵头的上海材料基因组工程研究院成立;2016年2月4日,北京材料基因工程创新联盟成立。新型能源材料,包括锂(离子)全固态电池和锂离子无机固体电解质,均是重要的研究方向。

图1 固态电解质筛选流程图[36]
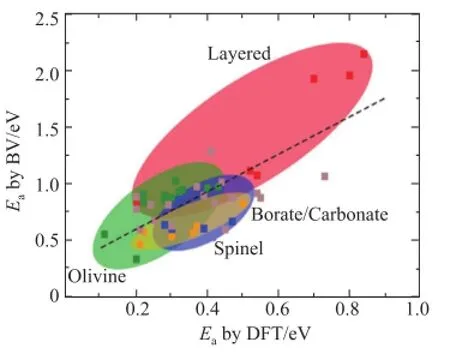
图2 基于BV方法和DFT方法计算锂离子输运活化能(Ea)[38]
2 常见锂离子无机固体电解质材料的精确计算研究进展
电解质材料位于正负极材料之间,起到输运离子、隔绝电子的作用。因此,以实际应用为导向,对于无机固体电解质材料的计算研究大多集中在高电导率材料的成分/组分优化、扩散系数、输运机制,以及相对于电极材料以及环境的稳定性等方面。由于快离子导体中常常有过量的锂离子可占据位置,因此建立无序的结构模型通常是理论计算的难点之一。无序常常会有助于锂离子的协同跃迁,这需要采用原子尺度的计算方法来阐明其中的输运机理。下面分别就常见的固体电解质材料(结构如图1(a)~1(d)所示)简述其部分计算的研究进展。
1977年,Goodenough和Hong等[39]提出高电导率NASICON (Na SuperIonic CONductor)型锂离子无机固体电解质材料LiM2(PO4)3,其中MO6八面体和PO4四面体组成共价的[M1M2P3O12]-骨架,导电锂离子分布在骨架中形成三维的锂离子通道。锂离子存在的两种占位类型A1和A2,纯相中A1位占满而A2位留空,低价掺杂可以使A2位部分占据。Francisco等[40]将第一性原理计算与实验结果相结合,对不同占据模式导致的熵变进行了讨论。丰富的掺杂取代,使NASICON结构成为研究化学掺杂-晶体结构-导电性能关系的典型范例之一[41],其中Li1.3Al0.3Ti1.7(PO4)3具有最高的电导率[42-43]。然而,由于载流子浓度和迁移率的提高在实验上很难区分,该掺杂使电导率提高的机理并不明确。Aono等[44]提出Al掺杂导致的致密度提高和晶界电阻降低或许是其具有高电导率的本质原因。Nuspl等[45]利用分子力学和分子动力学方法模拟了纯相LiTi2(PO4)3以及Al掺杂体系中的锂离子扩散通道和活化能,证明了锂离子迁移势垒(0.30 eV)受Al掺杂的影响较小。但是,Lang等[46]利用第一性原理计算了LiTi2(PO4)3中Ti被不同元素取代后(LXTP, X可为3、4、5价元素)间隙位以及空位锂离子扩散的跃迁势垒,结果表明间隙位锂离子在遵循Knock-off机制时跃迁势垒低至0.19 eV。然而为了引入间隙位锂离子,用Al3+部分取代Ti4+将会导致锂离子“陷入”Al附近,反而使跃迁势垒提高。
1978年,Hong等[47]提出同样具有三维离子通道的LISICON(Li SuperIonic CONductor)结构,Li14Zn(GeO4)4,并可扩展为γ-Li3PO4体系(xLi4MIVO4—(1-x)Li3MVO4;MIV= Ge,Ti;MV=As,V),该体系仅在有限的浓度(x=0.4~0.6)和温度范围内可以形成固溶体纯相[48]。第一性原理方法主要用于计算周期性结构,对于该固溶体体系通常需要扩展晶胞以满足计量比要求,且该体系锂离子扩散过程中复杂的化学环境和多种输运机制给计算带来很大的挑战。Fujimura和Tanaka等[49]利用团簇展开法建立较宽范围的固溶体组分模型,确定有序—无序相转变温度以及多种掺杂/取代组分三元相图,并利用第一性原理分子动力学方法模拟了高温锂离子电导率;随后结合实验数据,利用机器学习的方法预测各个组分100 ℃的电导率,并系统地对该结构进行组成与电导率优化。然而,对于该体系的组分调控是有限的,且理论最大电导率仍不超过10-3S/cm。2000年,Kanno等[50]提出硫代LISICON结构(thio-LISICON)具有比氧系更高的电导率。2011年,Kamaya与Kanno等[51]报道了Li10GeP2S12,其室温锂离子电导率可高达10-2S/cm,并结合第一性原理计算确定其晶体结构。其四面体4d位的P/Ge分数占据为建模带来难度[52]。由经典[18]和第一性原理[53]分子动力学计算可得超快的一维锂离子通道,可动锂离子之间的强库仑相互作用导致“线状协同运动(stringlike cooperative ionic motion)”[54]。Du等[52]认为锂离子的扩散势垒与其配位环境相关,三种不同配位方式的一维通道势垒分别为0.16、0.20、0.29 eV,二维通道分别为0.37、0.27、0.24 eV。中子衍射结果表明低温时一维通道连通,高温时二维通道开始连通[55]。固态核磁共振结果证实了各向异性的三维通道,一维超快锂离子通道的活化能为0.16 eV,二维快锂离子通道的活化能为0.26 eV[56],均证实了计算结果。然而,考虑多体之间的范德华力时会得出三维通道的结论[57],且范德华力对于力学性质而言非常重要,计算表明材料具有较好的延展性。利用第一性原理计算衍生体系Li10±1MP2X12(M=Ge,Si,Sn,Al,P;X=O,S,Se)体的相图、电化学稳定性和电导率,表明取代导致的晶格参数减小会显著抑制锂离子输运,但是晶格参数增大对于电导率的提高并不明显。虽然氧化物具有更高的化学稳定性,但是氧原子替换硫原子会导致结构热稳定性下降,且氧化物电导率极低。此外,考虑到Ge对于Li负极通常不稳定,而Si和Sn不仅稳定且价格更便宜,计算表明Li10SiP2S12和Li10SnP2S12与Ge系材料性能相近[58](Sn[59-60]、Si[60-62]取代已被实验验证)。硫代γ-Li3PO4体系及其相应的纳米结构和玻璃态同样是研究热点。Liu等[63]认为β-Li3PS4是高电导率相;Yang等[64]利用第一性原理分子动力学计算了β-Li3PS4和γ-Li3PS4的扩散系数,认为前者更高的电导率来源于本征的锂空位,而具有更多缺陷位的纳米团簇中锂离子迁移率更高。Xiao等[38]利用BVM算得O部分取代S反而可以提高电导率。Ohara等[65]利用密度泛函理论和可逆蒙特卡洛方法,并结合实验结果分析二元Li2S-P2S5玻璃体系的相组分、局域结构以及电子结构,认为可通过调节PSx和LiSx多面体共享边的结构以及降低电子在P和桥接S之间的转移,来提高体系的电导率。
1953年,Brous等合成Li0.5La0.5TiO3钙钛矿型固体电解质。通过调节组分得到的Li3xLn2/3-x□1/3-2xTiO3本征存在晶格空位,可以用渗流机制模型定性地拟合电导率 σ与锂离子浓度n、空位浓度n′、渗流阈值xc的关系式:

这里,α为晶格扭曲导致局域无序度增加的修正项,扭曲可以忽略时α=0。在立方结构中,对于三维通道,xc=0.311 7,μ=2,拟合结果与实验浓度-电导率图符合很好[66-67]。1993至1994年,Inaguma等[68-69]发现Li0.33Ln0.56TiO3具有最高的电导率,然而由于O的电子2p轨道具有不对称性[70],实验中常发现二维的锂离子通道[13,71-72]。此时xc=0.296,μ=1.3。渗流模型先验地假定Li、La和空位的晶格位等价,而实际上钙钛矿具有富La层和贫La层的超晶格结构,且层间Li、La与空位占据存在无序性。这不仅造成其定量地偏离简单的渗流模型,亦提高了第一性原理计算的建模难度[73]。Nakayama等[74]结合团簇展开、蒙特卡洛方法和第一性原理计算,得到La和空位与温度相关的排列方式。Catti等根据实验结果建立各个组分相应的空间群模型,通过静电势分布推测锂离子最可能的占据位置[75]或通过基态能计算确定最稳定Li-La-空位分布[76-77]。Tanaka等[70]通过分析锂离子扩散能面中能谷的构型特征,预测锂离子分布方式以及对应的输运通道。Jay和Kilner等[78]创新地利用遗传算法(genetic algorithm),使子构型不断继承高离子电导率局域序结构的“父体(富La层)”和“母体(贫La层)”的“基因”,最终“繁衍”出高电导率结构。以上结构模型建立后,锂离子输运机制的研究就顺理成章,其与Li/La/空位组分以及层内/层间序结构均有很大关系。然而,该类材料总电导率限制因素常归因于过高的晶界电阻。Moriwake等[79]构造了直角的畴界,解释实验上观察到的畴现象[80-81],但是该模型并不能解释复杂得多的实际晶界。
2003年Weppner等[82]发现石榴石(Garnet)结构Li5La3M2O12(M=Ta,Nb)具有较高的离子电导率和较宽的电化学窗口,且因其相对于金属Li稳定而受到关注。2007年Murugan等[83]发现Li7La3Zr2O12,室温离子电导率超过10-4S/ cm。石榴石通式为,其中孤立的(SiO4)四面体四个顶角与(B3+O6)八面体顶角相连,A2+在十二面体空隙中。其锂离子化合物变体LixLa3M2O12(x=3~7.5;M=W,Te,Ta,Nb,Zr,Y,…)中,M占据B位,La占据A位,Li在3个四面体(原结构中的Si位)以及6个八面体(原结构中为空)位占据,分配方式与锂含量有关,且锂离子之间由于相互作用而尽量远离。极限值为3时仅有四面体位占据,7.5时一半四面体24 d和全部八面体位中的一半96 h位占据[84]。“stuffed”的锂占据方式为该体系实验研究的热点之一[14,84-87]。Wang等[88]利用逆向蒙特卡洛法和经典分子动力学方法,以Li5La3Ta2O12为例研究锂的局域结构和热力学分布。Adams等[89]和Bernstein等[90]以Li7La3Zr2O12为例,利用键价方法、分子动力学和第一性原理计算等方法,研究其锂离子分布以及温度相关的相变。实验表明Li含量在6.5左右时四方相—立方相转变温度较低,且室温电导率可高达10-3S/cm[91]。Bernstein等[90]解释相变机理:四方相中锂离子有序分布,立方相中锂离子无序分布,相变伴随着锂的重新分布和晶格向高对称性扭曲;引入锂空位可以增加构型熵,缓解立方相无序化带来的能量增加,导致更低的四方—立方相转变温度。Santosh等[92]通过第一性原理计算,认为锂空位缺陷生成能较低,或许可以带来额外的非化学计量比空位。四面体的Li是否参与锂离子输运在实验研究中被长期争论[93]。Xu等[94]利用第一性原理计算研究了立方相不同锂含量石榴石结构LixLa3M2O12(x=3,5,7;M=Te,Nb,Zr)的锂离子占据方式和跃迁势垒。根据不同含量的锂离子配位推测可知:x=3,锂离子倾向于占据四面体位,基本不可跃迁;x=5,八面体位锂离子倾向于绕过四面体锂占据位跃迁,势垒约为0.8 eV;x=7,锂离子倾向于经过四面体空位在八面体之间跃迁,势垒约为0.3 eV;实际活化能为不同跃迁方式的几率平均[94]。然而,Wang等[88]认为x=5时锂离子也不会绕过四面体,以八面体—八面体方式直接跃迁。Adams等[89]认为四面体不参与锂离子迁移,但四面体和八面体锂离子通道并不是分离的,四面体的占据会阻碍锂离子在八面体之间有效跃迁,因此可以通过M位高价掺杂等方式引入足够的四面体空位来提高电导率。可注意到,Al掺杂可以有效稳定立方相,增加空位浓度,提高电导率[15],计算证实了Al在Li位的掺杂方式[95]。无序的空位有助于载流子协同运动,计算表明协同输运机制广泛存在于Li7La3Zr2O12[96-97]和Li5La3Ta2O12
[98]中。为了优化电导率,Miara等[99]计算不同掺杂后证实,增加晶胞参数不会显著提高电导率,减小晶胞参数会快速降低电导率,且锂离子电导率与空位和锂的浓度均相关。因此,异价掺杂使得锂离子与四面体/八面体锂空位浓度适中并保持立方结构,是优化电导率的方向。考虑到实际应用环境的(电)化学与机械性能稳定,计算研究了LixLa3M2O12与H2O/CO2[100]界面、Li[101]和LiCoO2电极材料[102]界面的稳定性及其弹性性质[103]。
2012年,Zhao等[104]基于钙钛矿ABX3结构,用一价阳离子Li+占据X位得到富锂材料,并用-1价的卤族元素和-2价的O分别来替代A位和B位。此时材料中元素的电性与传统钙钛矿材料相反,且具有高锂离子浓度,因此称之为“富锂的反钙钛矿材料” (Lithium-rich anti-perovskites, LiRAP),其中Li3OCl0.5Br0.5具有该体系最高的室温电导率(6.05×10-3S/cm)。Deng等[105]根据不同卤化物局域环境的锂离子跃迁势垒建立键渗流模型,认为0.235≤x≤0.395时Li3OCl1-xBrx具有更高的电导率,并利用第一性原理分子动力学证实Li3OCl0.75Br0.25扩散系数高于Li3OCl0.5Br0.5。计算表明反钙钛矿是亚稳态,0 K时单相Li3OA(A=Cl,Br)相对于混合相Li2O和LiA能量更高[106-108],但是可以通过提高温度超过550 K获得[108]。Chen等[109]通过计算声子谱发现Li3OCl力学不稳定,Li6O八面体的倾斜将降低整体能量,但当温度超过480 K时振动熵可以稳定其结构。Zhao等[104]提出材料制备的热处理历史导致微观结构的变化,例如空位增多、结构扭曲(如八面体的倾斜)、局域无序等,这为确定载流子类型以及研究微观输运机制带来难度。活化能实验值也并不统一(0.18 eV[104]和0.36 eV[110])。Zhang等[106]利用第一性原理的分子动力学方法,认为当材料存在锂空位时可以在熔点以下获得超离子相变(亚晶格融化)。Zhang等[106]和Deng等[105]均认为材料遵循空位跃迁,活化能为0.3~0.4 eV。Emly等[107]认为材料中的主要缺陷为电中性的弗兰克缺陷对,协同输运机制跃迁势垒为0.15 eV。Mouta等[108,111]则用经典原子准静态计算,推断材料中的主要缺陷为LiCl肖脱基缺陷对,锂空位的迁移势垒约为0.3 eV。由于电荷补偿机制,肖脱基缺陷可以提高间隙锂缺陷浓度,推填子机制跃迁时势垒约为0.1 eV。Lu等[112]利用第一性原理计算该体系电中性缺陷对和导致的间隙锂和空位锂的缺陷生成能和迁移能,并利用经典分子动力学研究其扩散机理,支持肖脱基缺陷对以及锂空位跃迁,其经过Cl空位路径的活化能<0.34 eV。计算均表明本征缺陷浓度依然十分低,难以达到实验得到的电导率。因此空位/间隙位输运机制以及不同的活化能,可能归结于不同制备过程中[104,110]非本征缺陷浓度的过量程度、卤素的耗损以及无序结构导致的协同输运机制。如何调控和优化电导率,目前仍未有定论。关于该材料的电化学窗口,亦有一定争议性:Zhang等[106]算得电化学窗口接近5 eV;Braga等[113]算出电子能隙为6.44 eV,130 ℃的循环伏安实验表明实际的稳定范围超过8 V;Emly等[107]通过计算锂化学势-组分相图发现,虽然Li3OCl具有超过5 eV的带隙,然而当对其施加2.5 V偏压时,反钙钛矿材料倾向于分解为Li2O2、LiCl和LiClO4。
3 小结与展望
锂离子无机固体电解质材料的应用有希望提高锂(离子)电池的安全性和能量密度,但获取可以和有机液体电解质电导率(>1 mS/cm)比拟的材料依旧是一项挑战。利用材料基因组的思想将计算、数据库与实验结合,有希望提高无机固体电解质材料的研发和优化速度,以满足应用需求,包括高的电导率、良好的机械性能、对环境以及正负极的稳定性等。本文从材料的高通量筛选以及针对特定材料的精确计算两方面,综述锂离子无机固体电解质的计算研究进展。从材料的筛选与设计方面,新型高性能材料仍有待于进一步的研究和探索。从特定材料的机理研究方面,快离子导体具有无序性与载流子协同输运的特征[114],其所涉及的关键物理问题可能更为复杂,仍然缺乏深入的认识,例如无序的晶体结构模型、快离子导体的相变机制、协同运动的微观机制、载流子与骨架离子/载流子与电子之间的相互作用以及晶体结构与高电导率之间的构效关系等等,而第一性原理计算与分子动力学模拟提供了微观机理研究的有力工具。对于全固态电池而言,界面电阻常常是问题的关键,实际界面不仅要考虑复杂的空间电荷层,而且还需要考虑互扩散导致的有限固溶体组分、由于晶格匹配造成的应力、界面形貌/分形与纳米结构等复杂的问题,这不仅包括长期以来有关纳米/团簇计算的挑战,也涉及实际充放电中由动力学控制的结构演化/热力学非平衡过程,需要从多时间-空间尺度来综合考虑。
(2016年5月4日收稿)■
[1] FISCHER C C, TIBBETTS K J, MORGAN D, et al. Predicting crystal structure by merging data mining with quantum mechanics [J]. Nat Mater, 2006, 5(8): 641-646.
[2] HAUTIER G, FISCHER C C, JAIN A, et al. Finding nature's missing ternary oxide compounds using machine learning and density functional theory [J]. Chem Mater, 2010, 22(12): 3762-3767.
[3] HAUTIER G, FISCHER C, EHRLACHER V, et al. Data mined ionic substitutions for the discovery of new compounds [J]. Inorg Chem, 2011, 50(2): 656-663.
[4] CEDER G. Opportunities and challenges for frst-principles materials design and applications to Li battery materials [J]. MRS Bull, 2010, 35(9): 693-701.
[5] CEDER G, HAUTIER G, JAIN A, et al. Recharging lithium battery research with frst-principles methods [J]. MRS Bull, 2011, 36(3): 185-191.
[6] JAIN A, ONG S P, HAUTIER G, et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation [J]. APL Mater, 2013, 1(1): 011002.
[7] WANG Y, RICHARDS W D, ONG S P, et al. Design principles for solid-state lithium superionic conductors [J]. Nat Mater, 2015, 14(10): 1026-1031.
[8] RICHARDS W D, MIARA L J, WANG Y, et al. Interface stability in solid-state batteries [J]. Chem Mater, 2016, 28(1): 266-273.
[9] ZHU Y, HE X, MO Y. First principles study on electrochemical and chemical stability of solid electrolyte-electrode interfaces in all-solidstate Li-ion batteries [J]. J Mater Chem A, 2016, 4(9): 3253-3266.
[10] ZHU Y, HE X, MO Y. Origin of outstanding stability in the lithium solid electrolyte materials: insights from thermodynamic analyses based on first-principles calculations [J]. ACS Applied Materials & Interfaces, 2015, 7(42): 23685-23693.
[11] DENG Z, WANG Z, CHU I H, et al. Elastic properties of alkali superionic conductor electrolytes from frst principles calculations [J]. J Electrochem Soc, 2016, 163(2): A67-A74.
[12] RADHAKRISHNAN B, ONG S P. Aqueous stability of alkali superionic conductors from frst-principles calculations [J]. Frontiers in Energy Research, 2016. doi: 10.3389/fenrg.2016.00016.
[13] YASHIMA M, ITOH M, INAGUMA Y, et al. Crystal structure and diffusion path in the fast lithium-ion conductor La0.62Li0.16TiO3[J]. J Am Chem Soc, 2005, 127(10): 3491-3495.
[14] HAN J T, ZHU J L, LI Y T, et al. Experimental visualization of lithium conduction pathways in garnet-type Li7La3Zr2O12[J]. Chem Commun, 2012, 48(79): 9840-9842.
[15] GEIGER C A, ALEKSEEV E, LAZIC B, et al. Crystal chemistry and stability of “Li7La3Zr2O12” garnet: A fast lithium-ion conductor [J]. Inorg Chem, 2011, 50(3): 1089-1097.
[16] LI W, WU G T, ARAUJO C M, et al. Li+ion conductivity and diffusion mechanism in α-Li3N and β-Li3N [J]. Energ Environ Sci, 2010, 3(10): 1524-1530.
[17] ADAMS S, RAO R P. Ion transport and phase transition in Li7-xLa3(Zr2-xMx)O12(M=Ta5+, Nb5+, x=0, 0.25) [J]. J Mater Chem, 2012, 22(4): 1426-1434.
[18] ADAMS S, RAO R P. Structural requirements for fast lithium ion migration in Li10GeP2S12[J]. J Mater Chem, 2012, 22(16): 7687-7691.
[19] ADAMS S, SWENSON J. Pathway models for fast ion conductors by combination of bond valence and reverse Monte Carlo methods [J].Solid State Ionics, 2002, 154: 151-159.
[20] ADAMS S. Bond valence analysis of structure-property relationships in solid electrolytes [J]. J Power Sources, 2006, 159(1): 200-204.
[21] THANGADURAI V, ADAMS S, WEPPNER W. Crystal structure revision and identifcation of Li+-ion migration pathways in the garnetlike Li5La3M2O12(M=Nb, Ta) oxides [J]. Chem Mater, 2004, 16(16): 2998-3006.
[22] ANUROVA N A, BLATOV V A. Analysis of ion-migration paths in inorganic frameworks by means of tilings and Voronoi-Dirichlet partition: a comparison [J]. Acta Crystallogr B, 2009, 65: 426-434.
[23] NUSPL G, TAKEUCHI T, WEISS A, et al. Lithium ion migration pathways in LiTi2(PO4)3and related materials [J]. J Appl Phys, 1999, 86(10): 5484-5491.
[24] FILSO M O, TURNER M J, GIBBS G V, et al. Visualizing lithium-ion migration pathways in battery materials [J]. Chem-Eur J, 2013, 19(46): 15535-15544.
[25] BROWN I D. Recent developments in the methods and applications of the bond valence model [J]. Chem Rev, 2009, 109(12): 6858-6919.
[26] GONZALEZ-PLATAS J, GONZALEZ-SILGO C, RUIZ-PEREZ C. VALMAP2.0: contour maps using the bond-valence-sum method [J]. J Appl Crystallogr, 1999, 32: 341-344.
[27] ADAMS S, SWENSON J. Determining ionic conductivity from structural models of fast ionic conductors [J]. Phys Rev Lett, 2000, 84(18): 4144-4147.
[28] ADAMS S, RAO R P. Understanding ionic conduction and energy storage materials with bond-valence-based methods [M]//BROWN I D, POEPPELMEIER K R (eds). Bond Valences. [S. l.]: Springer Berlin Heidelberg, 2014: 129-159.
[29] ADAMS S. Relationship between bond valence and bond softness of alkali halides and chalcogenides [J]. Acta Crystallogr B, 2001, 57: 278-287.
[30] ADAMS S, TAN E S. Pathways for ion transport in nanostructured BaF2: CaF2[J]. Solid State Ionics, 2008, 179(1-6): 33-37.
[31] ADAMS S. From bond valence maps to energy landscapes for mobile ions in ion-conducting solids [J]. Solid State Ionics, 2006, 177: 1625-1630.
[32] ADAMS S. SoftBV web pages [M]. Göttingen: Universität Göttingen, 2003.
[33] ADAMS S, RAO R P. High power lithium ion battery materials by computational design [J]. Phys Status Solidi A, 2011, 208(8): 1746-1753.
[34] ADAMS S, RAO R P. Transport pathways for mobile ions in disordered solids from the analysis of energy-scaled bond-valence mismatch landscapes [J]. Phys Chem Chem Phys, 2009, 11(17): 3210-3216.
[35] AVDEEV M, SALE M, ADAMS S, et al. Screening of the alkali-metal ion containing materials from the inorganic crystal structure database (ICSD) for high ionic conductivity pathways using the bond valence method [J]. Solid State Ionics, 2012, 225: 43-46.
[36] GAO J, CHU G, HE M, et al. Screening possible solid electrolytes by calculating the conduction pathways using bond valence method [J]. Sci China Phys Mech Astron, 2014, 57(8): 1526-1536.
[37] XIAO R, LI H, CHEN L. Candidate structures for inorganic lithium solid-state electrolytes identified by high-throughput bond-valence calculations [J]. Journal of Materiomics, 2015, 1(4): 325-332.
[38] XIAO R, LI H, CHEN L. High-throughput design and optimization of fast lithium ion conductors by the combination of bond-valence method and density functional theory [J]. Sci Rep, 2015, 5: 14227.
[39] TAYLOR B E, ENGLISH A D, BERZINS T. New solid ionic conductors [J]. Materials Research Bulletin, 1977, 12(2): 171-181.
[40] FRANCISCO B E, STOLDT C R, MPEKO J C. Energetics of ion transport in Nasicon-type electrolytes [J]. Journal of Physical Chemistry C, 2015, 119(29): 16432-16442.
[41] ANANTHARAMULU N, RAO K K, RAMBABU G, et al. A wideranging review on Nasicon type materials [J]. J Mater Sci, 2011, 46(9): 2821-2837.
[42] AONO H, SUGIMOTO E, SADAOKA Y, et al. Ionic conductivity of solid electrolytes based on lithium titanium phosphate [J]. J Electrochem Soc, 1990, 137(4): 1023-1027.
[43] AONO H, SUGIMOTO E, SADAOKA Y, et al. Ionic-conductivity of the lithium titanium phosphate (Li1+xAlxTi2-x(PO4)3), (Li1+xScxTi2-x(PO4)3), (Li1+xYxTi2-x(PO4)3), (Li1+xLaxTi2-x(PO4)3systems [J]. J Electrochem Soc, 1989, 136(2): 590-591.
[44] AONO H, SUGIMOTO E, SADAOKA Y, et al. Electrical property and sinterability of LiTi2(PO4)3mixed with lithium salt (Li3PO4or Li3PO3) [J]. Solid State Ionics, 1991, 47(3/4): 257-264.
[45] NUSPL G, TAKEUCHI T, WEIB A, et al. Lithium ion migration pathways in LiTi2(PO4)3and related materials [J]. J Appl Phys, 1999, 86(10): 5484-5491.
[46] LANG B, ZIEBARTH B, ELSAESSER C. Lithium ion conduction in LiTi2(PO4)3and related compounds based on the Nasicon structure: A frst-principles study [J]. Chem Mater, 2015, 27(14): 5040-5048.
[47] HONG H Y P. Crystal structure and ionic conductivity of Li14Zn(GeO4)4and other new Li+superionic conductors [J]. Materials Research Bulletin, 1978, 13(2): 117-124.
[48] BRUCE P G, WEST A R. Phase-diagram of the lisicon, solid electrolyte system, Li4GeO4-Zn2GeO4[J]. Materials Research Bulletin, 1980, 15(3): 379-385.
[49] FUJIMURA K, SEKO A, KOYAMA Y, et al. Accelerated materials design of lithium superionic conductors based on first-principles calculations and machine learning algorithms [J]. Adv Energy Mater, 2013, 3(8): 980-985.
[50] KANNO R, MARUYAMA M. Lithium ionic conductor thio-LISICON. The Li2S-GeS2-P2S5system [J]. J Electrochem Soc, 2001, 148(7): A742-A746.
[51] KAMAYA N, HOMMA K, YAMAKAWA Y, et al. A lithium superionic conductor [J]. Nat Mater, 2011, 10(9): 682-686.
[52] DU F, REN X, YANG J, et al. Structures, thermodynamics, and Li+mobility of Li10GeP2S12: a first-principles analysis [J]. Journal of Physical Chemistry C, 2014, 118(20): 10590-10595.
[53] MO Y, ONG S P, CEDER G. First principles study of the Li10GeP2S12lithium super ionic conductor material [J]. Chem Mater, 2012, 24(1): 15-17.
[54] XU M, DING J, MA E. One-dimensional stringlike cooperative migration of lithium ions in an ultrafast ionic conductor [J]. Appl Phys Lett, 2012, 101: 031901. doi: 10.1063/1.4737397.
[55] KWON O, HIRAYAMA M, SUZUKI K, et al. Synthesis, structure, and conduction mechanism of the lithium superionic conductor Li10+δGe1+δP2-δS12[J]. J Mater Chem A, 2015, 3(1): 438-446.
[56] LIANG X, WANG L, JIANG Y, et al. In-channel and in-plane Li ion diffusions in the superionic conductor Li10GeP2S12probed by solidstate NMR [J]. Chem Mater, 2015, 27(16): 5503-5510.
[57] HU C H, WANG Z Q, SUN Z Y, et al. Insights into structural stability and Li superionic conductivity of Li10GeP2S12from first-principles calculations [J]. Chemical Physics Letters, 2014, 591: 16-20.
[58] ONG S P, MO Y, RICHARDS W D, et al. Phase stability, electrochemical stability and ionic conductivity of the Li10±1MP2X12(M=Ge, Si, Sn, Al or P, and X=O, S or Se) family of superionicconductors [J]. Energy & Environmental Science, 2013, 6(1): 148-156.
[59] BRON P, JOHANSSON S, ZICK K, et al. Li10SnP2S12: An affordable lithium superionic conductor [J]. Journal of the American Chemical Society, 2013, 135(42): 15694-15697.
[60] KATO Y, SAITO R, SAKANO M, et al. Synthesis, structure and lithium ionic conductivity of solid solutions of Li10(Ge1-xMx)P2S12(M = Si, Sn) [J]. Journal of Power Sources, 2014, 271: 60-64.
[61] WHITELEY J M, WOO J H, HU E, et al. Empowering the lithium metal battery through a silicon-based superionic conductor [J]. J Electrochem Soc, 2014, 161(12): A1812-A1817.
[62] KUHN A, GERBIG O, ZHU C, et al. A new ultrafast superionic Liconductor: ion dynamics in Li11Si2PS12and comparison with other tetragonal LGPS-type electrolytes [J]. Physical Chemistry Chemical Physics, 2014, 16(28): 14669-14674.
[63] LIU Z, FU W, PAYZANT E A, et al. Anomalous high ionic conductivity of nanoporous β-Li3PS4[J]. J Am Chem Soc, 2013, 135(3): 975-978.
[64] YANG J, TSE J S. First-principles molecular simulations of Li diffusion in solid electrolytes Li3PS4[J]. Computational Materials Science, 2015, 107: 134-138.
[65] OHARA K, MITSUI A, MORI M, et al. Structural and electronic features of binary Li2S-P2S5glasses [J]. Scientific Reports, 2016, 6: 21302.
[66] INAGUMA Y, ITOH M. Infuences of carrier concentration and site percolation on lithium ion conductivity in perovskite-type oxides [J]. Solid State Ionics, 1996, 86-88: 257-260.
[67] KATSUMATA T, MATSUI Y, INAGUMA Y, et al. Influence of site percolation and local distortion on lithium ion conductivity in perovskite-type oxides La0.55Li0.35-xKxTiO3and La0.55Li0.35TiO3-KMO3(M=Nb and Ta) [J]. Solid State Ionics, 1996, 86-88: 165-169.
[68] INAGUMA Y, CHEN L Q, ITOH M, et al. High ionic-conductivity in lithium lanthanum titanate [J]. Solid State Commun, 1993, 86(10): 689-693.
[69] INAGUMA Y, CHEN L Q, ITOH M, et al. Candidate compounds with perovskite structure for high lithium ionic-conductivity [J]. Solid State Ionics, 1994, 70: 196-202.
[70] TANAKA Y, OHNO T. Two dimensional Li diffusion in ion-conductive lithium lanthanum titanates [J]. ECS Electrochemistry Letters, 2013, 2(7): A53-A55.
[71] EMERY J, BUZARE J Y, BOHNKE O, et al. Lithium-7 NMR and ionic conductivity studies of lanthanum lithium titanate electrolytes [J]. Solid State Ionics, 1997, 99(1/2): 41-51.
[72] BOHNKE O, EMERY J, FOURQUET J L. Anomalies in Li+ion dynamics observed by impedance spectroscopy and Li-7 NMR in the perovskite fast ion conductor (Li3xLa2/3-x□1/3-2x)TiO3[J]. Solid State Ionics, 2003, 158(1/2): 119-132.
[73] OHARA K, KAWAKITA Y, PUSZTAI L, et al. Structural disorder in lithium lanthanum titanate: the basis of superionic conduction [J]. Journal of Physics: Condensed Matter, 2010, 22(40): 404203.
[74] NAKAYAMA M, SHIRASAWA A, SAITO T. Arrangement of La and vacancies in La2/3TiO3predicted by frst-principles density functional calculation with cluster expansion and Monte Carlo simulation [J]. Journal of the Ceramic Society of Japan, 2009, 117(1368): 911-916.
[75] CATTI M. First-principles modeling of lithium ordering in the LLTO (LixLa2/3-x/3TiO3) superionic conductor [J]. Chem Mater, 2007, 19(16): 3963-3972.
[76] CATTI M. Ion mobility pathways of the Li+conductor Li0.125La0.625TiO3by ab initio simulations [J]. Journal of Physical Chemistry C, 2008, 112(29): 11068-11074.
[77] CATTI M. Short-range order and Li+ion diffusion mechanisms in Li5La9□2(TiO3)16(LLTO) [J]. Solid State Ionics, 2011, 183(1): 1-6.
[78] JAY E E, RUSHTON M J D, CHRONEOS A, et al. Genetics of superionic conductivity in lithium lanthanum titanates [J]. Phys Chem Chem Phys, 2015, 17(1): 178-183.
[79] MORIWAKE H, GAO X, KUWABARA A, et al. Domain boundaries and their influence on Li migration in solid-state electrolyte (La,Li) TiO3[J]. J Power Sources, 2015, 276: 203-207.
[80] GAO X, FISHER C A J, KIMURA T, et al. Lithium atom and A-site vacancy distributions in lanthanum lithium titanate [J]. Chem Mater, 2013, 25(9): 1607-1614.
[81] GAO X, FISHER C A J, KIMURA T, et al. Domain boundary structures in lanthanum lithium titanates [J]. J Mater Chem A, 2014, 2(3): 843-852.
[82] THANGADURAI V, KAACK H, WEPPNER W J F. Novel fast lithium ion conduction in garnet-type Li5La3M2O12(M=Nb, Ta) [J]. J Am Ceram Soc, 2003, 86(3): 437-440.
[83] MURUGAN R, THANGADURAI V, WEPPNER W. Fast lithium ion conduction in garnet-type Li7La3Zr2O12[J]. Angew Chem Int Ed Engl, 2007, 46(41): 7778-7781.
[84] XIE H, ALONSO J A, LI Y, et al. Lithium distribution in aluminumfree cubic Li7La3Zr2O12[J]. Chem Mater, 2011, 23(16): 3587-3589.
[85] CUSSEN E J. The structure of lithium garnets: cation disorder and clustering in a new family of fast Li+conductors [J]. Chem Commun, 2006, 4: 412-413.
[86] VAN WULLEN L, ECHELMEYER T, MEYER H W, et al. The mechanism of Li-ion transport in the garnet Li5La3Nb2O12[J]. Physical Chemistry Chemical Physics, 2007, 9(25): 3298-3303.
[87] O'CALLAGHAN M P, CUSSEN E J. Lithium dimer formation in the Li-conducting garnets Li5+xBaxLa3-xTa2O12(0<x≤1.6) [J]. Chem Commun, 2007, 20: 2048-2050.
[88] WANG Y X, KLENK M, PAGE K, et al. Local structure and dynamics of lithium garnet ionic conductors: A model material Li5La3Ta2O12[J]. Chem Mater, 2014, 26(19): 5613-5624.
[89] ADAMS S, RAO R P. Ion transport and phase transition in Li7-xLa3(Zr2-xMx)O12(M=Ta5+, Nb5+, x=0, 0.25) [J]. J Mater Chem, 2012, 22(4): 1426-1434.
[90] BERNSTEIN N, JOHANNES M D, HOANG K. Origin of the structural phase transition in Li7La3Zr2O12[J]. Phys Rev Lett, 2012, 109(20): 205702.
[91] LI Y, HAN J T, WANG C A, et al. Optimizing Li+conductivity in a garnet framework [J]. J Mater Chem, 2012, 22(30): 15357.
[92] SANTOSH K C, LONGO R C, XIONG K, et al. Point defects in garnet-type solid electrolyte (c-Li7La3Zr2O12) for Li-ion batteries [J]. Solid State Ionics, 2014, 261: 100-105.
[93] ZEIER W G. Structural limitations for optimizing garnet-type solid electrolytes: a perspective [J]. Dalton Transactions, 2014, 43(43): 16133-16138.
[94] XU M, PARK M S, LEE J M, et al. Mechanisms of Li+transport in garnet-type cubic Li3+xLa3M2O12(M=Te, Nb, Zr) [J]. Phys Rev B, 2012, 85(5): 052301. doi: 10.1103/phys Rev B. 85.052301.
[95] RETTENWANDER D, BLAHA P, LASKOWSKI R, et al. DFT study of the role of Al in the fast ion-conductor Li7-3xAl3+xLa3Zr2O12garnet [J]. Chem Mater, 2014, 26(8): 2617-2623.
[96] JALEM R, YAMAMOTO Y, SHIIBA H, et al. Concerted migration mechanism in the Li ion dynamics of garnet-type Li7La3Zr2O12[J]. Chem Mater, 2013, 25(3): 425-430.
[97] MEIER K, LAINO T, CURIONI A. Solid-state electrolytes: Revealing the mechanisms of Li-ion conduction in tetragonal and cubic LLZO byfrst-principles calculations [J]. The Journal of Physical Chemistry C, 2014, 118(13): 6668-6679.
[98] JAEM R, NAKAYAMA M, MANALASTAS W, et al. Insights into the lithium-ion conduction mechanism of garnet-type cubic Li5La3Ta2O12by ab-initio calculations [J]. Journal of Physical Chemistry C, 2015, 119(36): 20783-20791.
[99] MIARA L J, ONG S P, MO Y, et al. Effect of Rb and Ta doping on the ionic conductivity and stability of the garnet Li7+2x-y(La3-xRbx)(Zr2-yTay) O12(0≤x≤0.375, 0≤y≤1) superionic conductor: a first principles investigation [J]. Chem Mater, 2013, 25(15): 3048-3055.
[100] KANG S G, SHOLL D S. First-principles study of chemical stability of the lithium oxide garnets Li7La3M2O12(M=Zr, Sn, or Hf) [J]. The Journal of Physical Chemistry C, 2014, 118(31): 17402-17406.
[101] NAKAYAMA M, KOTOBUKI M, MUNAKATA H, et al. Firstprinciples density functional calculation of electrochemical stability of fast Li ion conducting garnet-type oxides [J]. Phys Chem Chem Phys, 2012, 14(28): 10008-10014.
[102] MIARA L J, RICHARDS W D, WANG Y E, et al. First-principles studies on cation dopants and electrolyte|cathode interphases for lithium garnets [J]. Chem Mater, 2015, 27(11): 4040-4047.
[103] YU S, SCHMIDT R D, GARCIA-MENDEZ R, et al. Elastic properties of the solid electrolyte Li7La3Zr2O12(LLZO) [J]. Chem Mater, 2016, 28(1): 197-206.
[104] ZHAO Y, DAEMEN L L. Superionic conductivity in lithium-rich antiperovskites [J]. J Am Chem Soc, 2012, 134(36): 15042-15047.
[105] DENG Z, RADHAKRISHNAN B, ONG S P. Rational composition optimization of the lithium-rich Li3OCl1-xBrxanti-perovskite superionic conductors [J]. Chem Mater, 2015, 27(10): 3749-3755.
[106] ZHANG Y, ZHAO Y, CHEN C. Ab initio study of the stabilities of and mechanism of superionic transport in lithium-rich antiperovskites [J]. Phys Rev B, 2013, 87(13): 134303. doi: 10.1103/PhysRevB.87.134303.
[107] EMLY A, KIOUPAKIS E, VAN DER VEN A. Phase stability and transport mechanisms in antiperovskite Li3OCl and Li3OBr superionic conductors [J]. Chem Mater, 2013, 25(23): 4663-4670.
[108] MOUTA R, MELO M Á B, DINIZ E M, et al. Concentration of charge carriers, migration, and stability in Li3OCl solid electrolytes [J]. Chem Mater, 2014, 26(24): 7137-7144.
[109] CHEN M H, EMLY A, VAN DER VEN A. Anharmonicity and phase stability of antiperovskite Li3OCl [J]. Phys Rev B, 2015, 91(21): 214306.
[110] LU X, WU G, HOWARD J W, et al. Li-rich anti-perovskite Li3OCl films with enhanced ionic conductivity [J]. Chem Commun, 2014, 50(78): 11520-11522.
[111] MOUTA R, DINIZ E M, PASCHOAL C W A. Li+interstitials as the charge carriers in superionic lithium-rich anti-perovskites [J]. J Mater Chem A, 2016, 4(5): 1586-1590.
[112] LU Z, CHEN C, BAIYEE Z M, et al. Defect chemistry and lithium transport in Li3OCl anti-perovskite superionic conductors [J]. Phys Chem Chem Phys, 2015, 17(48): 32547-32555.
[113] BRAGA M H, FERREIRA J A, STOCKHAUSEN V, et al. Novel Li3ClO based glasses with superionic properties for lithium batteries [J]. J Mater Chem A, 2014, 2(15): 5470-5480.
[114] GAO J, ZHAO Y S, SHI S Q, et al. Lithium-ion transport in inorganic solid state electrolyte [J]. Chin Phys B, 25(1): 018211.
(编辑:沈美芳)
Calculating investigations of inorganic solid-state electrolytes for Li-ion battery
GAO Jian①, HE Bing②, SHI Siqi①③
①Materials Genome Institute, Shanghai University, Shanghai 200444, China; ②School of Computer Engineering and Science, Shanghai University, Shanghai 200444, China; ③School of Materials Science and Engineering, Shanghai University, Shanghai 200444, China
The high throughput calculations can be used to mine the structure-activity relationship and accelerate the discovery of novel materials. The exact frst-principles calculations can predict the crystal structure, electronic structure, defects, phase diagram and phase transition, and the transport mechanisms of ions and electrons. This review is focused on the developments and perspectives in inorganic solid-state electrolytes calculating investigations, including the effective and effcient optimizing, screening and designing for the solid electrolytes with high conductivities, wide electrochemical windows, and proper compatibilities with electrodes.
Li-ion battery, inorganic solid-state electrolyte, materials genome initiative, high-throughput calculation, frst-principles calculation
10.3969/j.issn.0253-9608.2016.05.004
*国家自然科学基金(51622207、51372228、U1630134)资助
†通信作者,国家优秀青年科学基金获得者,研究方向:电化学能量存储材料的第一性原理计算和设计。E-mail: sqshi@shu.edu.cn
