热电材料中自旋轨道耦合效应对电输运的影响*

吴立华，杨炯，李鑫，骆军，张文清

上海大学材料基因组工程研究院，上海 200444

热电材料中自旋轨道耦合效应对电输运的影响*

吴立华，杨炯，李鑫，骆军，张文清†

上海大学材料基因组工程研究院，上海 200444

自旋量子效应对材料电输运性质的影响，是一个物理和材料领域的基础问题。热电材料能够实现电能和热能相互转换，其往往含有重元素，自旋轨道耦合效应对电性能的影响不容忽视。自旋轨道耦合造成的Zeeman型能带劈裂效应降低能带带边的简并度和能态密度，对热电材料的输运性质不利；而自旋熵和Rashba型自旋劈裂效应对热电性质有益，其中的Rashba自旋劈裂效应能够产生新奇的低维化电输运。拓扑绝缘体中非平庸电子结构对电输运调控提供新的方向。

热电材料；自旋轨道耦合；电子能带；电输运

半导体热电材料利用塞贝克效应和帕尔贴效应实现温差发电或电制冷，被应用在空间用特种电源、汽车尾气废热或工业余热发电、电子器件制冷等领域。相比于其他能量转换技术，热电材料构成的器件具有无污染、可靠性高、无需运动组件和无需光源等优势，但其能量转换效率仍旧较低。提高材料的热电性能，是优化热电器件能量转换效率的第一步。高性能热电材料应具有高的塞贝克系数(同等温差下高的电动势)、低的电阻率和热导率，而这些物理参数本身相互关联，协同优化这些物性是热电材料研究的核心。本质上，优化热电性能就是同时调控电子和声子的输运性质。近年来，填充方钴矿等“电子晶体-声子玻璃”体系[1-2]、相变体系[3-4]、半晶态体系[5-6]和铅硫族纳米材料[7-9]等呈现出优异的热电性能。

热电材料的带边电子结构对其电输运起决定作用[10]。在常规热电材料研究中，电子内禀的自旋量子效应对电子结构和电输运的影响，往往被涵盖在理论计算中或者被忽略。近年来，自旋量子效应在自旋电子学和凝聚态物理等领域受到很多关注。自旋轨道耦合效应造成的非平庸电子结构，使得相关基础物理性质、材料性能的调控不同寻常。在固体材料中，电子总是处于离子实和电子云产生的势能梯度中，这一势能梯度即局域的内建电场，其作用于运动的电子可产生一个有效磁场，有效磁场与电子自旋的作用就是自旋轨道耦合效应[11]。热电材料往往含有重元素，因此具有强自旋轨道耦合效应，这一效应对电子结构和电子输运的影响是一个物理和材料的基础问题。本文将讨论自旋轨道耦合效应对电子能带的影响，重点关注自旋熵、Zeeman型能带劈裂和Rashba型自旋劈裂效应对热电材料电输运的作用，同时也将涉及自旋轨道耦合造成的非平庸电子结构对热电性质的可能贡献。

1 自旋轨道耦合效应对电子能带的影响

在单个原子中，自旋轨道耦合效应的典型作用是使简并原子能级发生分裂；而在由原子周期性排列构成的固体材料中，自旋轨道耦合效应则对电子能带施加影响。固体能带被影响的程度与自旋轨道耦合的强度、固体材料的结构对称性等密切相关[11]。在没有外加磁场时，体系保持时间反演对称性，即朝反方向运动的自旋相反电子应具有相同能量：

其中，k为波矢，↑↓表示两种自旋态。当固体保持晶体结构的中心反演对称性时，电子还满足：

在时间反演和中心反演对称性都保持时，自旋轨道耦合效应可造成能带的劈裂[12]。如图1(a)所示，自旋轨道耦合造成两条能带之间具有劈裂能量ΔSOC。这一现象在具有中心对称性的半导体中很常见，如Ge的价带顶，劈裂的能带仍自旋简并。然而当时间反演对称性破缺时，如外加磁场，等式(1)不再成立，能带会出现Zeeman型自旋劈裂，即不同自旋态对应的能带之间出现能量差，如图1(b)所示。能带带边的简并度降低，能态密度减小。图1(a)和1(b)两种情形的劈裂可以看成Zeeman型能带劈裂。

在中心对称性破缺时，自旋轨道耦合效应可能造成Dresselhaus效应[13-14]或Rashba效应[15-18]，分别如图1(c)和1(d)所示。它们的共同特征是，不同自旋态对应的能带沿着不同波矢方向劈裂，带底偏离倒空间高对称次轴。此时，等式(2)不再成立，但两条能带仍保持能量简并。InSb、GaAs等具有闪锌矿结构的III-V族化合物，波矢为非零时发生Dresselhaus效应；而CdS、ZnS等具有纤锌矿结构的体系，则具有Rashba效应。这两种效应的差别是，Dresselhaus和Rashba效应的劈裂大小分别正比于波矢的三次方和一次方，因此，Rashba效应在带边劈裂的程度明显强于Dresselhaus效应。如图1(d)所示，常将Rashba效应中的波矢偏移量定义为k0，Rashba能量定义为E0，表征Rashba强度的参量定义为αR，三个参数在抛物带近似下满足αR=2E0/k0。非对称体系的自旋轨道耦合效应和内建电场越强，Rashba劈裂效应越强，αR也就越大。早期的Rashba效应研究主要关注整体结构对称性破缺的二维低维体系[19-21]，但从2011年以来，三维块体材料BiTeI和GeTe被发现具有巨Rashba效应[22-23]。

图1 自旋轨道耦合效应对电子能带的影响示意图。(a)自旋轨道耦合效应造成中心对称体系的Zeeman型能带劈裂，能带仍具有自旋简并； (b) 时间反演对称性破缺造成的Zeeman型能带劈裂，能带无自旋简并；晶体结构中心反演对称性破缺造成的(c) Dresselhaus效应和(d)Rashba效应

2 典型自旋轨道耦合效应对电输运的影响

2.1 自旋熵

物理本质上，热电材料的塞贝克系数衡量了固体中载流子的熵。在NaxCoO2等钴金属氧化物中，磁性Co离子具有3+和4+的不同价态，增加了自旋和轨道自由度，也就增加了电子排布的构型熵和塞贝克系数[24-25]。图2显示了不同价态Co离子呈现的低、中和高自旋态，每种状态下电子构型的可能性(即简并度)标注在框内[26]。钴的变价导致体系的电子构型熵增大，自旋熵对塞贝克系数的额外贡献可以表示成：

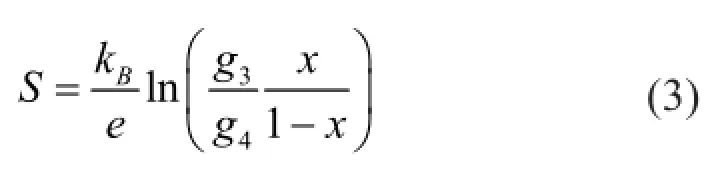
其中，x是四价钴的比例，g3和g4分别是三价和四价钴离子的电子构型简并度。低、中和高三种自旋态的能量接近，这无疑增大了体系的简并度；同时，不同价态Co离子的比例对电学输运很重要。由于自旋熵的贡献，NaxCoO2体系的300 K塞贝克系数高达100 μV/K，电导率仍如同金属，功率因子比Bi2Te3还高[24]。过渡金属氧化物的自旋熵为热电体系设计提供了新的思路。

图2 不同价态Co离子呈现的低自旋态(LS state)、中自旋态(IS state)和高自旋态(HS state)[26](其中，横线代表eg和t2g轨道，箭头代表一个电子自旋，总自旋角动量和每个状态的简并度分别显示在方框下和方框内)

2.2 Zeeman型能带劈裂效应

自旋效应往往造成能带带边的Zeeman型劈裂，而带边结构恰对热电材料的电输运起关键作用，Zeeman型能带劈裂效应一般对热电材料的电学输运不利。例如，自旋轨道耦合效应造成Mg2X(X=Si，Ge，Sn)体系价带顶的能带劈裂，并显著影响了其热电性能[27]。如图3(a)所示，Mg2Sn的价带在布里渊区Γ点处出现了劈裂(虚线为计入自旋轨道耦合效应的能带)。Mg2X(X= Si，Ge，Sn) 体系Zeeman型劈裂程度随着X原子序数的增加逐渐变强，Mg2Si、Mg2Ge和Mg2Sn的劈裂能量ΔSOC分别达到了36 meV、208 meV和525 meV。图3(b)显示了自旋轨道耦合效应对Mg2Sn塞贝克系数的影响规律：不考虑极高温的双极扩散效应，在P型导电时，价带顶的劈裂显著降低塞贝克系数；而在N型导电的情形下，自旋轨道耦合效应对塞贝克系数的影响很小，这是由于其对导带结构几乎没有影响。价带的Zeeman型劈裂造成了能态密度的降低，也等效成有效质量的减小，塞贝克系数减少，热电性能变差。外加磁场破坏时间反演对称性，材料则会出现Zeeman型自旋劈裂，同样也会降低带边的能态密度，不利于热电性能。例如， Na0.68CoO2体系在外加磁场后发生Zeeman型自旋劈裂[28]，外加磁场使其同等温度下的塞贝克系数明显降低，而且磁场越强，塞贝克系数越低。图4总结了Zeeman型能带劈裂效应对电子能带、能态密度和塞贝克系数的影响规律。两种情形下，能带在能量空间的劈裂造成带边电子能态密度和塞贝克系数的下降。

图3 (a)自旋轨道耦合效应对Mg2Sn的价带顶能带结构的影响[27]；(b)Mg2Sn在70 K、300 K和900 K温度下塞贝克系数与载流子浓度的关系[27](实线和虚线分别表示不计入和计入自旋轨道耦合效应之后的结果)

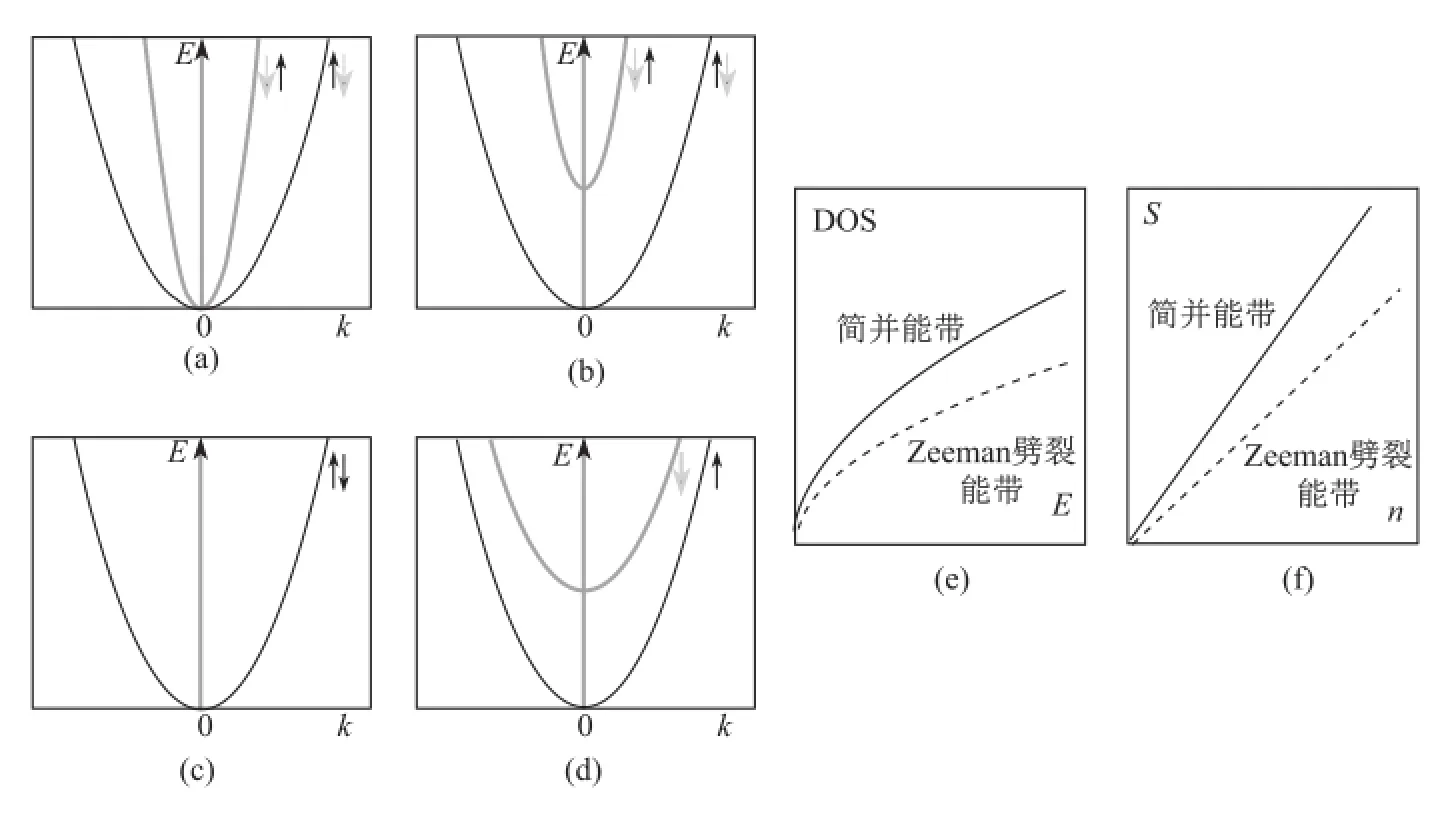
图4 Zeeman型能带劈裂效应对能带、能态密度和塞贝克系数影响的示意图。(a)双自旋简并能带在零点能量简并；(b)自旋轨道耦合造成能带(a)出现Zeeman型劈裂；(c)单自旋简并能带；(d)时间反演对称性破缺造成能带(c)出现Zeeman型自旋劈裂。两种情形的Zeeman型能带劈裂均使得(e)能态密度(DOS)降低和(f)塞贝克系数(S)变小

2.3 Rashba型自旋劈裂效应

Rashba效应使得不同自旋态的能带沿着相反波矢方向偏移，这造成费米面拓扑结构发生变化，二维和三维体系分别呈现圆环和甜甜圈形状[29]。理论研究发现，Rashba体系独特的费米面同时造成了能态密度和电学输运的低维化[30-31]，并在BiTeI和BiTeBr体系中被实验证实[31-32]。低维化的电学输运对热电性质非常有利，在带边能态密度突变附近可能造成巨热电效应[33-34]。

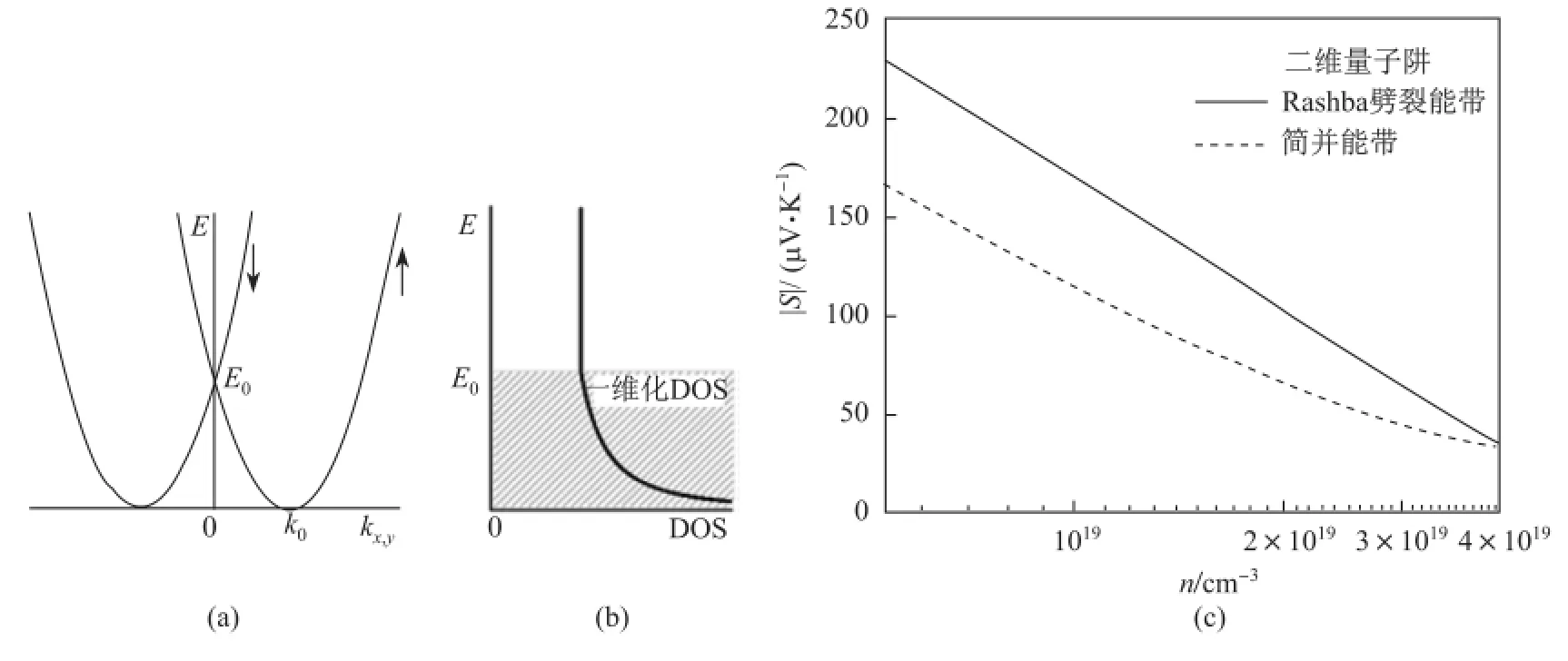
图5 Rashba型自旋劈裂效应对(a)二维量子阱能带、(b)能态密度和(c)塞贝克系数的影响[30]

二维体系成为新热电材料，主要是由于其好的电性能以及低的热导率[35]。常规二维量子阱具有自旋简并能带和恒定的能态密度，而由于自旋轨道耦合和结构对称性破缺，体系可能发生Rashba型自旋劈裂效应。具有强Rashba效应的二维体系包括Bi/Ag(111) 表面合金[20]、Bi单层或者量子薄膜[36-37]等。当费米能级低于Rashba能量E0时，能态密度具有一维化特征，如同一维纳米线体系(图5)，这可能对材料的超导电性产生有利影响(提高居里温度)[29]。从能态密度和弛豫时间近似出发，可以通过Boltzmann方程推导二维体系在自旋简并和Rashba自旋劈裂情形下的塞贝克系数S和载流子浓度n。构建一个以BiTeI作为阱材料的二维量子阱，厚度设定为2 nm，可以计算该Rashba型自旋劈裂体系的电输运性质。BiTeI的平面有效质量是0.09me(me是自由电子质量)，Rashba能量是0.113 eV[22,38-39]。我们选定温度是300 K，并考虑弛豫时间与温度无关，即散射因子r=0。计算结果表明[30]，在低载流子浓度区域，Rashba型自旋劈裂量子阱的塞贝克系数比自旋简并系统的要高40%左右(图5)，相应的电学参量S2n则为自旋简并体系的两倍。如果自旋劈裂和简并量子阱的迁移率和热导率相同，Rashba自旋劈裂体系的热电优值ZT就将两倍于自旋简并体系。

类似地，Rashba型三维块体材料在低费米能级区域具有二维化恒定的能态密度。基于抛物线带近似，利用输运理论可以系统对比块体中自旋劈裂与简并能带对电学输运的影响[31]。近几年来，具有强Rashba效应(大αR)的三维材料相继被发现，包括BiTeX (X=I，Br，Cl)[22,40-41]、α-GeTe[23]、α-SnTe[42]、LaOBiS2[42-43]和 AMX3(A=CH3NH3；M=Pb，Sn；X=I，Br)[44]。其中，BiTeI的导带底仅有Rashba劈裂能带，没有其他简并能带，将费米能级调控到该能量范围，可研究Rashba效应与电性能的关联。理论计算和实验表征如图6所示，计算结果与实验结果吻合得很好。与同等载流子浓度下的自旋简并体系相比较，Rashba型自旋劈裂体系具有更高的塞贝克系数S，电学参量S2n的提升也达到一倍。进一步的分析发现，BiTeI的塞贝克系数表现得如同一个2.67 nm厚的二维量子阱。Rashba型自旋劈裂体系之所以有更优异的热电性能，是因为低维化的能态密度造成同等载流子浓度时更低的费米能级，偏分电导的能量对称性更差，由Mott关系可知塞贝克系数更高。Xiao等[45]发现，Rashba型自旋劈裂材料中载流子的特殊散射机制也利于热电性质。目前，BiTeI这类Rashba型自旋劈裂体系的热电优值还不高，通过迁移率或带隙调控等手段可进一步提升其ZT[46-47]。

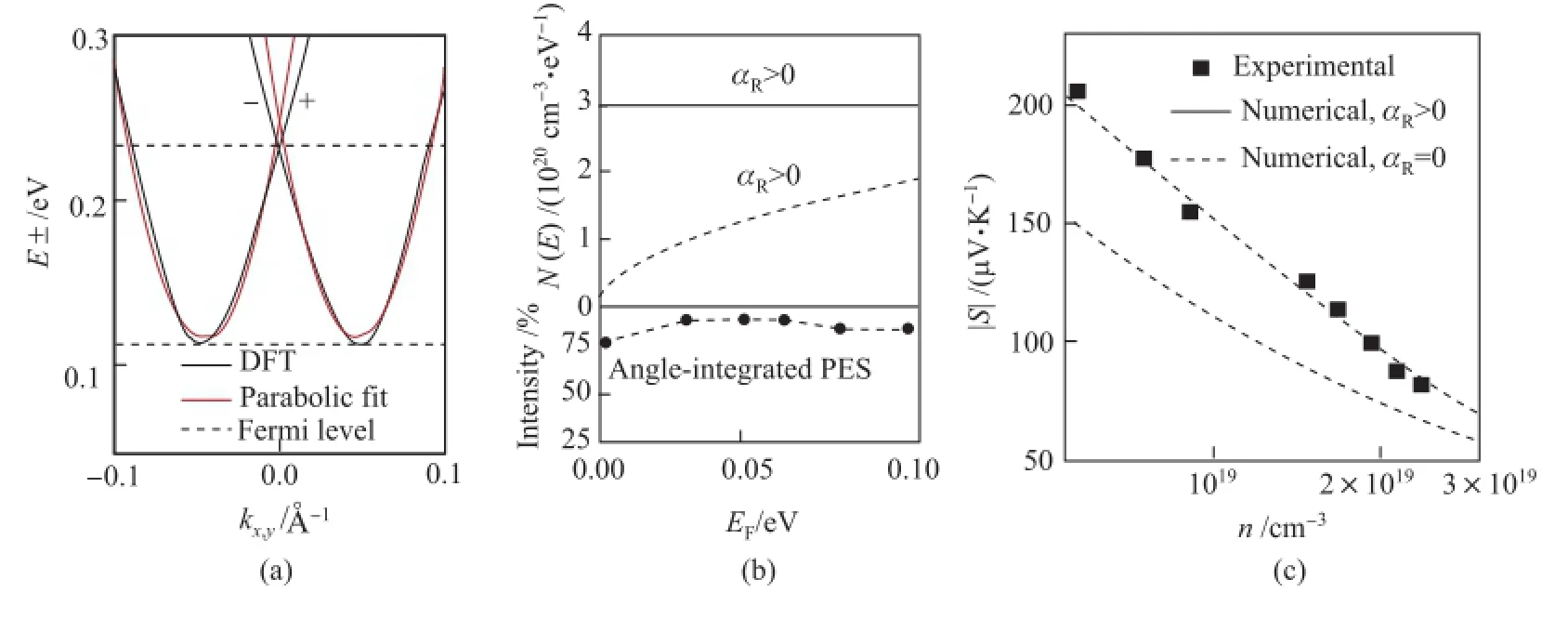
图6 块体材料BiTeI中Rashba型自旋劈裂效应对能带密度和塞贝克系数的影响[31]：(a)BiTeI的能带结构；(b)能态密度；(c)实验和理论塞贝克系数(其中，αR＞0表示Rashba自旋劈裂，αR=0表示自旋简并)

2.4 非平庸电子结构对电输运的影响

很多热电材料也具有拓扑绝缘性，非平庸电子结构对热电材料电输运的作用近年来受到较多关注[48-50]。热电材料和拓扑绝缘体的相似性主要包括重元素和窄带隙，重元素利于热导率的降低，而窄带隙则利于电输运性质[51]。当拓扑绝缘体的表面输运被考虑时，整体的电学性质将是材料表面和体电荷输运的耦合，其中表面电子的弛豫时间远大于体电子的弛豫时间。最近的研究表明[49]，拓扑绝缘体的表面、体电荷输运的耦合可能产生高的热电性能，体系尺寸的调控实现适当的表面、体电荷的协同输运。对于块体材料表面输运不重要时，拓扑绝缘体的能带翻转效应可能造成带边能带出现双带，符合能带简并的特征，能态密度得到提升，可能也对热电性质有利[52]。同时，Dirac和Weyl半金属的热电性质也不同于常规热电半导体[53]。相比于传统窄带隙热电半导体，零带隙的Dirac半金属的塞贝克系数可能很低，不是高性能热电材料[52]。这类体系的带边能带接近于线性带，导致载流子的有效质量和能带的能态密度很小；因而虽然载流子迁移率很高，但塞贝克系数和功率因子可能不理想，如Na3Bi。因此，非平庸电子结构对热电材料的电输运性质具有两面性。

3 总结与展望

热电材料中内禀的自旋轨道耦合效应对能带结构的影响与对称性密切相关，其对电输运性能的影响有利有弊。Zeeman型劈裂体系中劈裂能的存在显著降低能带的简并度和带边能态密度，塞贝克系数和总体电学输运性质明显低于能带简并体系；而Rashba型自旋劈裂引起费米面和能态密度的新奇变化，产生低维化电输运，对塞贝克系数和电学性质有利。近期发现的非平庸电子结构对热电材料的影响尚待继续探索，拓扑绝缘体体系的表面、体电荷输运的耦合可能产生高的热电性能。

(2016年5月4日收稿)■

[1] 席丽丽, 杨炯, 史迅, 等. 填充方钴矿热电材料: 从单填到多填[J]. 中国科学: 物理学 力学 天文学, 2011, 41: 1-23.

[2] SHI X, YANG J, SALVADOR J R, et al. Multiple-flled skutterudites: high thermoelectric figure of merit through separately optimizing electrical and thermal transports [J]. J Am Chem Soc, 2011, 133(20): 7837-7846.

[3] LIU H, SHI X, XU F, et al. Copper ion liquid-like thermoelectrics [J]. Nat Mater, 2012, 11(5): 422-425.

[4] ZHAO L D, LO S H, ZHANG Y, et al. Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals [J]. Nature, 2014, 508(7496): 373-377.

[5] QIU W, XI L, WEI P, et al. Part-crystalline part-liquid state and rattling-like thermal damping in materials with chemical-bond hierarchy [J]. Proc Natl Acad Sci USA, 2014, 111(42): 15031-15035.

[6] QIU W, WU L, KE X, et al. Diverse lattice dynamics in ternary Cu-Sb-Se compounds [J]. Sci Rep, 2015, 5: 13643.

[7] ZHAO L D, DRAVID V P, KANATZIDIS M G. The panoscopic approach to high performance thermoelectrics [J]. Energy Environ Sci, 2014, 7(1): 251-268.

[8] PEI Y, HEINZ N A, LALONDE A, et al. Combination of large nanostructures and complex band structure for high performance thermoelectric lead telluride [J]. Energy Environ Sci, 2011, 4(9): 3640-3645.

[9] BISWAS K, HE J, BLUM I D, et al. High-performance bulk thermoelectrics with all-scale hierarchical architectures [J]. Nature, 2012, 489(7416): 414-418.

[10] YANG J, XI L, QIU W, et al. On the tuning of electrical and thermal transport in thermoelectrics: an integrated theory-experiment perspective [J]. npj Computational Materials, 2016, 2: 15015.

[11] ZIMAN J M. Principles of the theory of solids [M]. London: Cambridge University Press, 1972.

[12] WINKLER R. Spin-orbit coupling effects in two-dimensional electron and hole systems [M]. Berlin Heidelberg: Springer, 2003.

[13] DRESSELHAUS G. Spin-orbit coupling effects in zinc blende structures [J]. Phys Rev, 1955, 100(2): 580-586.

[14] CARDONA M, CHRISTENSEN N, FASOL G. Relativistic band structure and spin-orbit splitting of zinc-blende-type semiconductors [J]. Phys Rev B, 1988, 38(3): 1806.

[15] RASHBA E I. Symmetry of energy bands in crystals of wurtzite type. 1. symmetry of bands disregarding spin-orbit interaction [J]. Sov Phys Solid State, 1959, 1(3): 368-380.

[16] RASHBA E, SHEKA V. Simmetriya energeticheskikh zon v kristallakh tipa vyurtsita. II. Simmetriya zon s uchyotom spinovykh vzaimodeistvii [J]. Fizika Tverd Tela, 1959, 1: 162-176.

[17] CASELLA R. Toroidal energy surfaces in crystals with wurtzite symmetry [J]. Phys Rev Lett, 1960, 5(8): 371.

[18] VOON L L Y, WILLATZEN M, CARDONA M, et al. Terms linear in k in the band structure of wurtzite-type semiconductors [J]. Phys Rev B, 1996, 53(16): 10703.

[19] HUANG S, BADRUTDINOV A, SERRA L, et al. Enhancement of Rashba coupling in vertical In0.05Ga0.95As/GaAs quantum dots [J]. Phys Rev B, 2011, 84(8): 085325.

[20] AST C R, HENK J, ERNST A, et al. Giant spin splitting through surface alloying [J]. Phys Rev Lett, 2007, 98(18): 186807.

[21] GIERZ I, SUZUKI T, FRANTZESKAKIS E, et al. Silicon surface with giant spin splitting [J]. Phys Rev Lett, 2009, 103(4): 046803.

[22] ISHIZAKA K, BAHRAMY M S, MURAKAWA H, et al. Giant Rashba-type spin splitting in bulk BiTeI [J]. Nat Mater, 2011, 10(7): 521-526.

[23] DI SANTE D, BARONE P, BERTACCO R, et al. Electric control of the giant rashba effect in bulk GeTe [J]. Adv Mater, 2013, 25(4): 509-513.

[24] TERASAKI I, SASAGO Y, UCHINOKURA K. Large thermoelectric power in NaCo2O4single crystals [J]. Phys Rev B, 1997, 56(20): R12685.

[25] WANG Y, ROGADO N S, CAVA R, et al. Spin entropy as the likely source of enhanced thermopower in NaxCo2O4[J]. Nature, 2003, 423(6938): 425-428.

[26] KOSHIBAE W, TSUTSUI K, MAEKAWA S. Thermopower in cobalt oxides [J]. Phys Rev B, 2000, 62(11): 6869.

[27] KUTORASINSKI K, WIENDLOCHA B, TOBOLA J, et al. Importance of relativistic effects in electronic structure and thermopower calculations for Mg2Si, Mg2Ge, and Mg2Sn [J]. Phys Rev B, 2014, 89(11): 115205.

[28] XIANG H J, SINGH D J. Suppression of thermopower of NaxCoO2by an external magnetic feld: Boltzmann transport combined with spinpolarized density functional theory [J]. Phys Rev B, 2007, 76(19): 195111.

[29] CAPPELLUTI E, GRIMALDI C, MARSIGLIO F. Topological change of the Fermi surface in low-density Rashba gases: application to superconductivity [J]. Phys Rev Lett, 2007, 98(16): 167002.

[30] WU L, YANG J, WANG S, et al. Thermopower enhancement in quantum wells with the Rashba effect [J]. Appl Phys Lett, 2014, 105(20): 202115.

[31] WU L, YANG J, WANG S, et al. Two-dimensional thermoelectrics with Rashba spin-split bands in bulk BiTeI [J]. Phys Rev B, 2014,90(19): 195210.

[32] SANS J, MANJÓN F, PEREIRA A, et al. Structural, vibrational, and electrical study of compressed BiTeBr [J]. Phys Rev B, 2016, 93(2): 024110.

[33] HICKS L D, DRESSELHAUS M S. Effect of quantum-well structures on the thermoelectric fgure of merit [J]. Phys Rev B, 1993, 47(19): 12727-12731.

[34] DRESSELHAUS M S, CHEN G, TANG M Y, et al. New directions for low-dimensional thermoelectric materials [J]. Adv Mater, 2007, 19(8): 1043-1053.

[35] VENKATASUBRAMANIAN R, SIIVOLA E, COLPITTS T, et al. Thin-flm thermoelectric devices with high room-temperature fgures of merit [J]. Nature, 2001, 413(6856): 597-602.

[36] GIERZ I, SUZUKI T, FRANTZESKAKIS E, et al. Silicon surface with giant spin splitting [J]. Phys Rev Lett, 2009, 103(4): 046803.

[37] MATHIAS S, RUFFING A, DEICKE F, et al. Quantum-well-induced giant spin-orbit splitting [J]. Phys Rev Lett, 2010, 104(6): 066802.

[38] BAHRAMY M S, ARITA R, NAGAOSA N. Origin of giant bulk Rashba splitting: Application to BiTeI [J]. Phys Rev B, 2011, 84(4): 041202.

[39] BORDÁCS S, CHECKELSKY J G, MURAKAWA H, et al. Landau level spectroscopy of dirac electrons in a polar semiconductor with giant Rashba spin splitting [J]. Phys Rev Lett, 2013, 111(16): 166403.

[40] EREMEEV S V, NECHAEV I A, KOROTEEV Y M, et al. Ideal twodimensional electron systems with a giant Rashba-type spin splitting in real materials: surfaces of bismuth tellurohalides [J]. Phys Rev Lett, 2012, 108(24): 246802.

[41] SAKANO M, BAHRAMY M S, KATAYAMA A, et al. Strongly spinorbit coupled two-dimensional electron gas emerging near the surface of polar semiconductors [J]. Phys Rev Lett, 2013, 110(10): 107204.

[42] ZHANG X, LIU Q, LUO J W, et al. Hidden spin polarization in inversion-symmetric bulk crystals [J]. Nat Phys, 2014, 10: 387.

[43] LIU Q, GUO Y, FREEMAN A J. Tunable Rashba effect in twodimensional LaOBiS2flms: Ultrathin candidates for spin feld effect transistors [J]. Nano Lett, 2013, 13(11): 5264-5270.

[44] KIM M, IM J, FREEMAN A J, et al. Switchable S=1/2 and J=1/2 Rashba bands in ferroelectric halide perovskites [J]. Proc Natl Acad Sci USA, 2014, 111(19): 6900-6904.

[45] XIAO C, LI D, MA Z. Unconventional thermoelectric behaviors and enhancement of fgure of merit in Rashba spintronic systems [J]. Phys Rev B, 2016, 93(7): 075150.

[46] WU L, YANG J, CHI M, et al. Enhanced thermoelectric performance in Cu-intercalated BiTeI by compensation weakening induced mobility improvement [J]. Sci Rep, 2015, 5: 14319.

[47] WU L, YANG J, ZHANG T, et al. Enhanced thermoelectric performance in the Rashba semiconductor BiTeI through band gap engineering [J]. J Phys: Condens Matter, 2016, 28(8): 085801.

[48] GHAEMI P, MONG R S, MOORE J E. In-plane transport and enhanced thermoelectric performance in thin flms of the topological insulators Bi2Te3and Bi2Se3[J]. Phys Rev Lett, 2010, 105 (16): 166603.

[49] XU Y, GAN Z, ZHANG S C. Enhanced thermoelectric performance and anomalous seebeck effects in topological insulators [J]. Phys Rev Lett, 2014, 112: 226801.

[50] SHI H, PARKER D, DU M H, et al. Connecting thermoelectric performance and topological-insulator behavior: Bi2Te3and Bi2Te2Se from frst principles [J]. Phys Rev Applied, 2015, 3(1): 014004.

[51] MÜCHLER L, CASPER F, YAN B, et al. Topological insulators and thermoelectric materials [J]. Phys Status Solidi RRL, 2013, 7(1/2): 91-100.

[52] PAL K, ANAND S, WAGHMARE U V. Thermoelectric properties of materials with nontrivial electronic topology [J]. J Mater Chem C, 2015, 3(46): 12130-12139.

[53] LUNDGREN R, LAURELL P, FIETE G A. Thermoelectric properties of Weyl and Dirac semimetals [J]. Phys Rev B, 2014, 90(16): 165115.

(编辑：沈美芳)

Influence of spin-orbital coupling on electrical transport for thermoelectric materials

WU Lihua, YANG Jiong, LI Xin, LUO Jun, ZHANG Wenqing
Materials Genome Institute, Shanghai University, Shanghai 200444, China

The infuence of spin-related quantum effected on electrical transport in materials is a fundamental question in the felds of physics and condensed matter. Thermoelectric materials normally contain heavy elements, where spin-orbital coupling effect can play an important role on the electronic band structure and electrical transport. The Zeeman-type band splitting effect induced by spin-orbital coupling can lower the band degeneracy and density of states, consequently deteriorate the Seebeck coeffcient and thermoelectric performance. In contrast, spin entropy and Rashba-type spin-splitting effect are benefcial to thermoelectric properties. The Rashba effect can lead to a low-dimensional transport phenomena, which raises the Seebeck coeffcient and overall thermoelectric performance. The non-trivial electronic band structures provide new directions for electrical transport in thermoelectric designs. In topological insulators, the coupling of bulk and surface transport may provide new approaches for optimizing electrical transport.

thermoelectric material, spin-orbital coupling, electronic band, electrical transport

10.3969/j.issn.0253-9608.2016.05.002

*国家自然科学基金(11234012、51572167、51632005、11604200)，上海市优秀学术带头人项目 (16XD1401100)和上海市自然科学基金(16ZR1448000)资助

†通信作者，国家杰出青年科学基金获得者，研究方向：计算材料科学与能量转换/储存材料的微观设计。E-mail: wqzhang@t.shu.edu.cn