直觉模糊时间序列

田宗浩，王 鹏

（陆军军官学院，合肥230031）

直觉模糊时间序列

田宗浩，王 鹏

（陆军军官学院，合肥230031）

针对模糊时间序列模型在处理数样本数据时存在局限性，引入直觉模糊集理论对模糊时间序列模型进行扩展。首先，通过对样本数据直觉模糊化，更加细腻地反映实际数据的不确定性本质；然后，在建立直觉模糊逻辑关系时引入犹豫度因子，更加真实地描述数据之间状态转换的不确定性，以Song、Chen和Lee提出的模型为框架，构建直觉模糊时间序列预测模型；最后，利用Alabama大学22年的入学人数为实验数据，对比分析Song、Chen和Lee模型及其加权模型的预测结果，验证了直觉模糊时间序列模型的可行性和优越性。

直觉模糊集；模糊时间序列；模糊逻辑关系；均方误差

自1993年Song和Chissom［1－3］首次提出基于模糊集理论的时间序列预测模型后，模糊时间序列（fuzzy time series，FTS）研究的脚步就一直没有停止。由于FTS能较好地处理含糊、不确定信息，且其模型具有良好的鲁棒性和泛化性，因此它在学术界和工程控制领域得到了广泛的重视。随着研究人员对模型的不断改进，其应用的范围不断扩展。同时FTS的局限性也逐渐显现出来：首先，普通模糊集的隶属度比较单一，不能形象地反映信息的含糊、不确定性；传统的FTS预测模型主要依据模糊逻辑关系的对应规则预测结果属性，忽略了预测值的随机依赖性，不能正确反映数据之间的随机变化特性。为此，模糊时间序列模型的扩展成为不可阻挡的趋势。

直觉模糊集［4］（intuitionistic fuzzy set，IFS）是对Zadeh教授提出的模糊集理论的扩展和补充。它通过增加一个非隶属度参数来描述事物“非此非彼”的模糊特性，其相应的数学描述更加符合客观世界的模糊本质，为处理不确定信息提供了新的研究思路。基于IFTS预测模型的理论刚刚起步，国内外相关的研究成果相对较少。Oscar等［5］首次将直觉模糊集推理融入到时间序列的分析中去，初步建立了直觉模糊时间序列（intuitionistic fuzzy time series，IFTS）预测模型，为提高FTS预测精度提供了新的研究方向。黎昌珍等［6］将时变的模糊时间序列推广到时变的直觉模糊时间序列。郑窛全［7］提出了一种基于IFCM聚类的时序预测模型。虽然这些成果提高了FTS的预测精度，但是模型缺乏标准的定义和相关的理论基础，尤其在样本数据直觉模糊化和模糊逻辑关系建立规则方面相对薄弱。为此，本文结合文献［4－7］，进一步完善IFTS模型的定义，将Song、Chen［8］和Lee［9］提出的FTS模型以及其相关的加权模型推广到直觉模糊范围，并通过实例验证IFTS预测模型的有效性。

1 基础理论

IFTS理论是FTS理论的延伸和扩展，其相应的定义和运算也是普通模糊集更一般的形式，鉴于此，依据文献［4－7］对IFTS的一些定义进行规范化。

定义1 Atanassov对直觉模糊集进行如下定义：

设X为给定的论域，则X上的一个直觉模糊集为

其中uA（x）：X→［0，1］，vA（x）：X→［0，1］分别表示A的隶属度函数和非隶属度函数，并且对于A上的所有x∈X总有0≤uA（x）＋vA（x）≤1成立。对于X上的一个直觉模糊集，πA（x）＝1－uA（x）－vA（x）称为A中x的直觉指数，表示x对A的一种不确定程度，因此普通的模糊集可以表示为A＝｛〈x，uA（x），1－uA（x）〉｜x∈X｝，直觉指数πA（x）＝0。

定义2 令Y（t），（t＝0，1，2，…）为论域U上的一个时间序列，论域U可以划分为n个语言变量U＝｛w1，w2，…，wn｝，则相应的时间序列Y（t）在U上可以用直觉模糊集F（t）的隶属度和非隶属度〈u1（Y（t）），v1（Y（t））〉来表示，其中u1（Y（t）），v1（Y（t））∈［0，1］，并且0≤u1（Y（t））＋v1（Y（t））≤1，则称F（t）为定义在Y（t）上的直觉模糊时间序列：

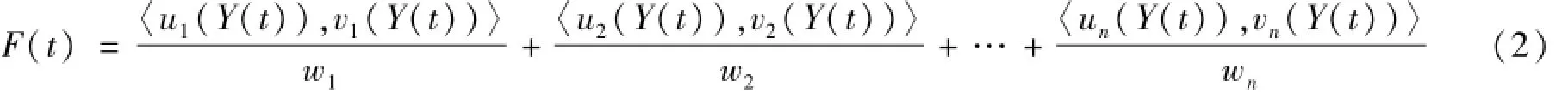
其中〈ui（Y（t）），vi（Y（t））〉是Y（t）相对于语言变量wi的隶属度和非隶属函数对，并且0≤ui（Y（t））＋vi（Y（t））≤1，F（t）为直觉模糊集，因此IFTS的样本数据必须直觉模糊化。

定义3 设R（t，t－1）为定义在F（t－1）和F（t）间的一阶直觉模糊关系，且满足F（t）＝F（t－1）。R（t，t－1），则称F（t）是由F（t－1）通过直觉模糊关系R（t，t－1）推导得到，F（t－1）和F（t）均为直觉模糊集。令F（t－1）＝Ai，F（t）＝Aj，则直觉模糊逻辑关系也可表示成Ai→Aj，其中：Ai称为直觉模糊逻辑关系的前件；Aj称为直觉模糊逻辑关系的后件。

定义4 对直觉模糊集之间的运算进行相关的定义，假设Ai＝｛〈μi，υi〉｝和Aj＝｛〈σj，γj〉｝，其中〈μi，υi〉和〈σj，γj〉分别为论域U上的隶属度和非隶属度函数对，则Ai和Aj之间的直觉模糊逻辑关系表示为

其中：T为转置符号；。为直觉模糊合成运算；Rij＝〈uRij，vij〉为直觉模糊关系矩阵的元素，并且

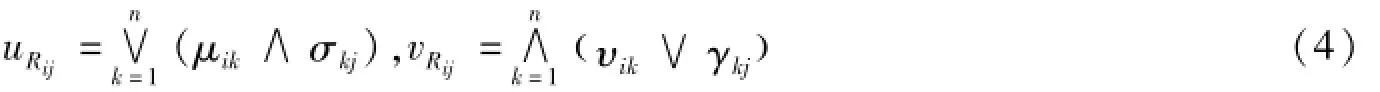
2 直觉模糊时间序列

模糊时间序列预测模型的关键是挖掘历史数据内部的模糊变化和不确定特性，掌握序列数据随时间的变化规律，提高预测结果的精度［10－11］。IFS通过增加非隶属度函数更加形象细腻地刻化模糊现象“非此非彼”的特性，反映实际状态变换的不确定性。因此，本文从样本数据直觉模糊化处理以及直觉模糊逻辑关系的建立层面入手，以传统Song、Chen和Lee提出的模糊时间序列模型框架以及它们对应的加权模型为基础，将模糊信息中的踌躇因素考虑到时序模型关系中去，构建直觉模糊时间序列预测模型，主要的建模步骤如下：

2.1 论域划分及序列数据直觉模糊化处理

若时间序列存在n个样本X＝｛x1，x2，…，xn｝，依据Song模型等分论域划分方法对样本数据进行划分。为对比需要，依旧采用7等分论域划分方法，对应的语义解释为：“极少”“很少”“少”“正常”“多”“很多”和“较多”，相应模糊概念的直觉模糊隶属函数为

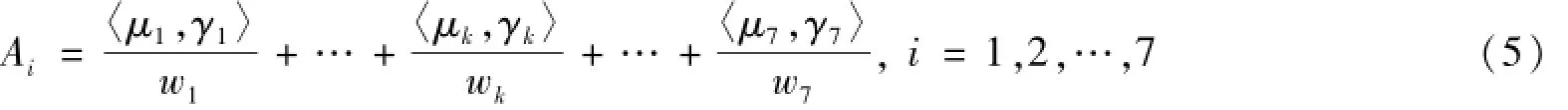
其中〈μk，γk〉表示对应模糊概念的隶属度和非隶属度函数对，具体的计算规则如下：

由定义2可知：IFTS的试验样本集应该为直觉模糊集，而现实中给出的样本数据大多为实数集。为此需要对样本数据进行直觉模糊化处理以满足建模的需要，本文利用式（6）对样本数据进行直觉模糊化处理。

其中：xj，j＝1，2，…，n为样本数据；l为等分论域区间间隔；mi为对应子区间的中间值；k为犹豫度，表示数据隶属集合的变异程度。依据式（6）即可对样本数据直觉模糊化，求出样本数据对每个模糊概念的隶属度和非隶属度函数对。

2.2 依据训练数据的先后建立直觉模糊关系矩阵

根据式（6）得到的样本直觉模糊化结果，按照最大隶属度和最小非隶属度原则，确定每个样本数据所对应的模糊概念。分别以Song、Chen和Lee提出的模糊逻辑关系确定方法为基础，推广建立相应的直觉模糊逻辑关系矩阵。

1）Song模型

为得到关系矩阵，传统的Song模型定义了一种“max－min”运算：

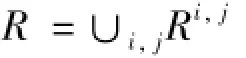
其中：“∪”为取矩阵Ri，j中元素最大值；Ri，j＝ATi×Aj，“×”为矩阵乘积取小运算。然而在IFTS中，样本集为直觉模糊集，依据IFS的运算性质，运用定义（4）将Song模型的关系矩阵扩展为直觉模糊关系矩阵，其对应的隶属度函数采用“max－min”运算，非隶属度函数采用“min－max”运算，因此R中的每个元素均为直觉模糊集。

2）Chen和Lee模型

在Chen模型中，模糊逻辑关系矩阵R是由Ai→Aj是否存在决定的，即如果出现Ai→Aj，则Rij＝1，否则Rij＝0；Lee模型为了更好地反映训练样本之间的模糊逻辑关系，采用Ai→Aj在训练集中出现的频率来建立模糊关系矩阵。然而在实际应用中，模糊状态之间的转换存在一些不确定的因素影响，导致Chen和Lee模型的模糊逻辑关系矩阵并不能很好地反映实际状态之间的转换关系。为此，引入犹豫度因子来反映状态之间转移的不确定性，其相应的直觉模糊逻辑关系确定方法为：设定一个犹豫度因子k，0≤k≤1，将k与模型的关系矩阵作用，将关系矩阵中的非零元素与1－k相乘，然后将k平分到关系矩阵每行与非零元素相邻的零元素位置（距离非零元素越远，状态变异的可能性就越小），以取代原来的零元素，这样得到的关系矩阵为带有犹豫度的直觉模糊逻辑关系矩阵。

2.3 预测去模糊化

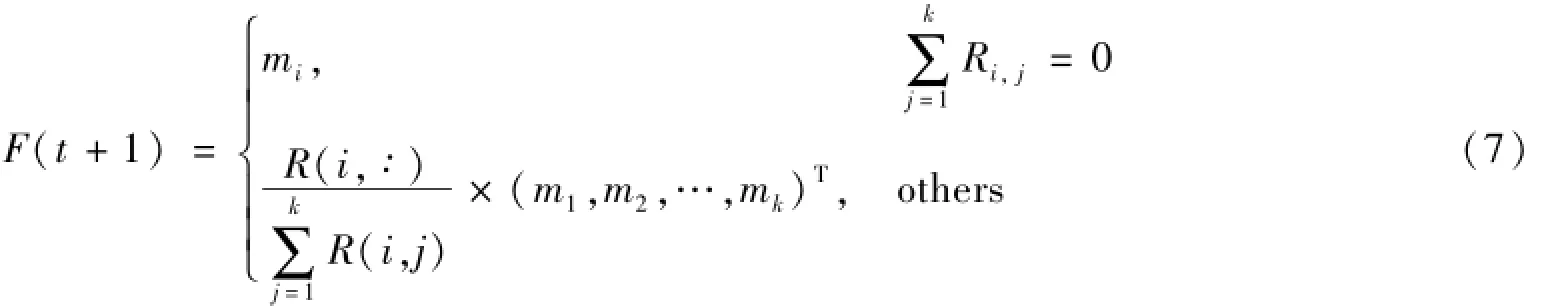
沿用Song提出的FTS的预测规则建立预测公式：其中：F（t＋1）为预测值；mk为对应模糊子集wk的中心值；R（i，：）为t时刻观测值对应模糊概念上直觉模糊集中隶属度最大值在关系矩阵R中的行向量的隶属度。

Song、Chen和Lee对应的加权模型充分考虑数据集隶属于每个模糊概念的隶属度，不仅仅局限于隶属度最大的位置。为此，将加权模型推广到IFTS，其预测公式为：

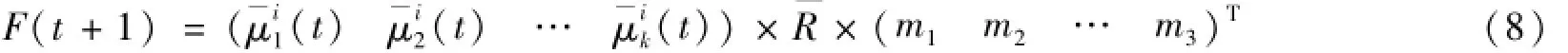
度向量，具体加权模型的相关运算见参考文献［12］。

为了说明模型的有效性，利用均方误差MSE来衡量模型的预测精度：

其中：x（t）为样本数据；F（t）为其对应的预测值。

3 算例分析

为验证IFTS模型的有效性，遵照本文方法建立IFTS模型的过程，利用Alabama大学22年的入学人数为实验数据，分别和Song、Chen和Lee模型以及其相应的加权模型进行对比分析。

步骤1 定义论域和数据直觉模糊化

依据文献［1－3］提出的均等论域划分方法，同样将样本数据划分为7个模糊子区间，以1 000为区间长度，则每个子区间为：w1＝［13 000，14 000］，w2＝［14 000，15 000］，…，w7＝［19 000，20 000］。由式（5）可定义直觉模糊集为：

由于Alabama大学22年的入学人数为实数集，而IFTS模型要求样本集为直觉模糊集，应用式（6）对样本数据直觉模糊化，直觉模糊化结果如下：

步骤2 建立直觉模糊逻辑关系

从步骤1可以得到每个样本值的直觉模糊化结果，按照时间先后顺序可得21个模糊关系，即：

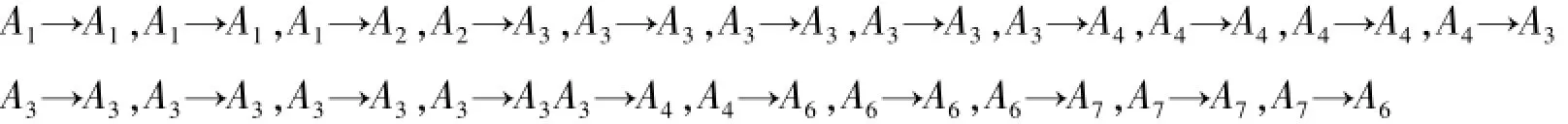
利用定义（4）可得Song模型直觉模糊逻辑关系矩阵为：

依据Chen和Lee模型中直觉模糊关系矩阵的建立的方法，可以得到直觉模糊关系矩阵RC和RL为：

其中k为犹豫度因子，0≤k≤1。

步骤3 预测与去模糊化

利用Song、Chen和Lee模型的预测算法，结合式（7）和（8）以及步骤2求出的直觉模糊关系矩阵，设定k＝0.05，分别得到推广到直觉模糊集范围模型的预测结果。在加权模型中，为了讨论的方便，仅仅考虑i＝2时的预测结果，对应直觉模糊模型的预测结果如表1所示，对应原模型的预测结果见参考文献［12］。

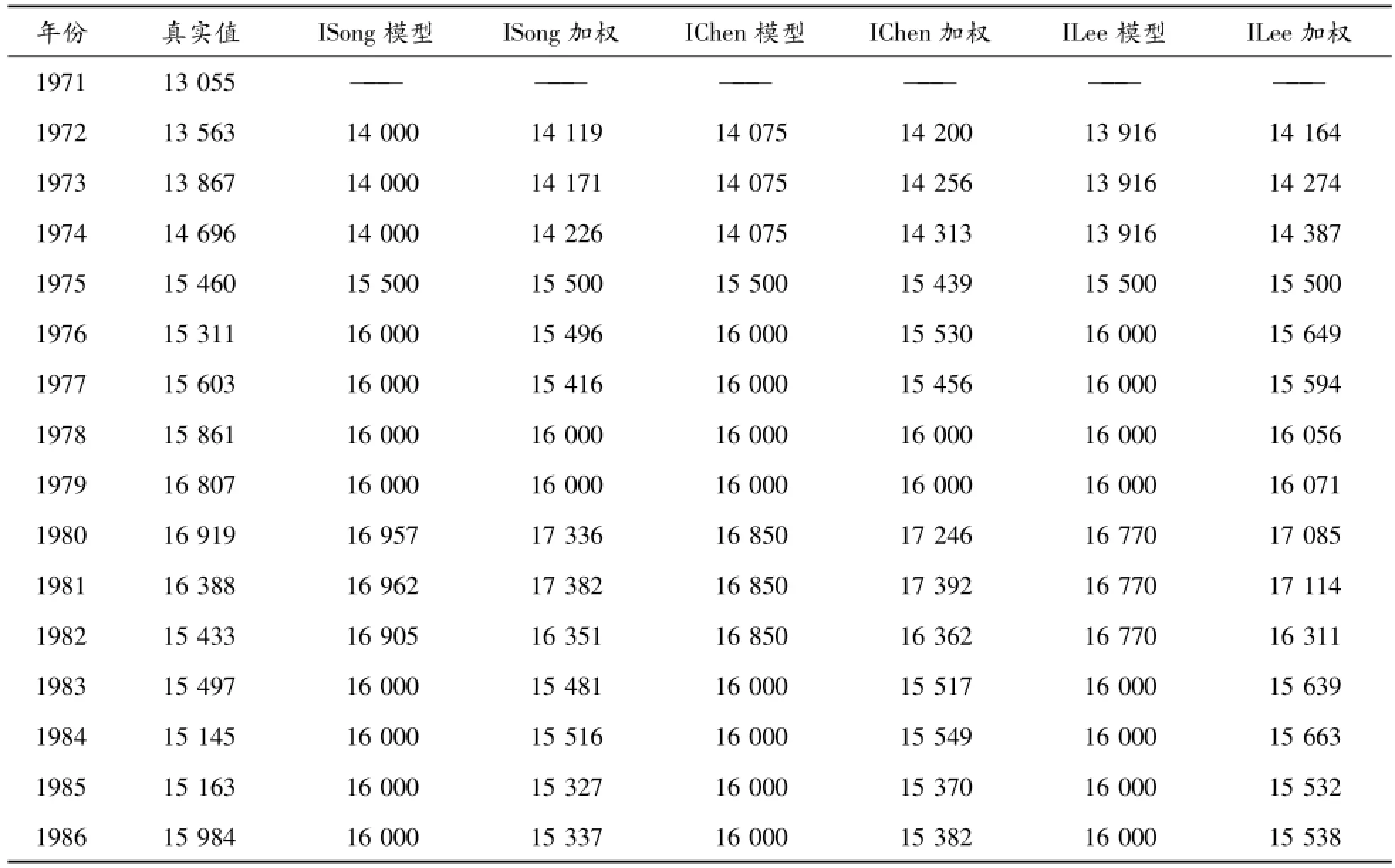
表1 相应直觉模糊模型预测结果

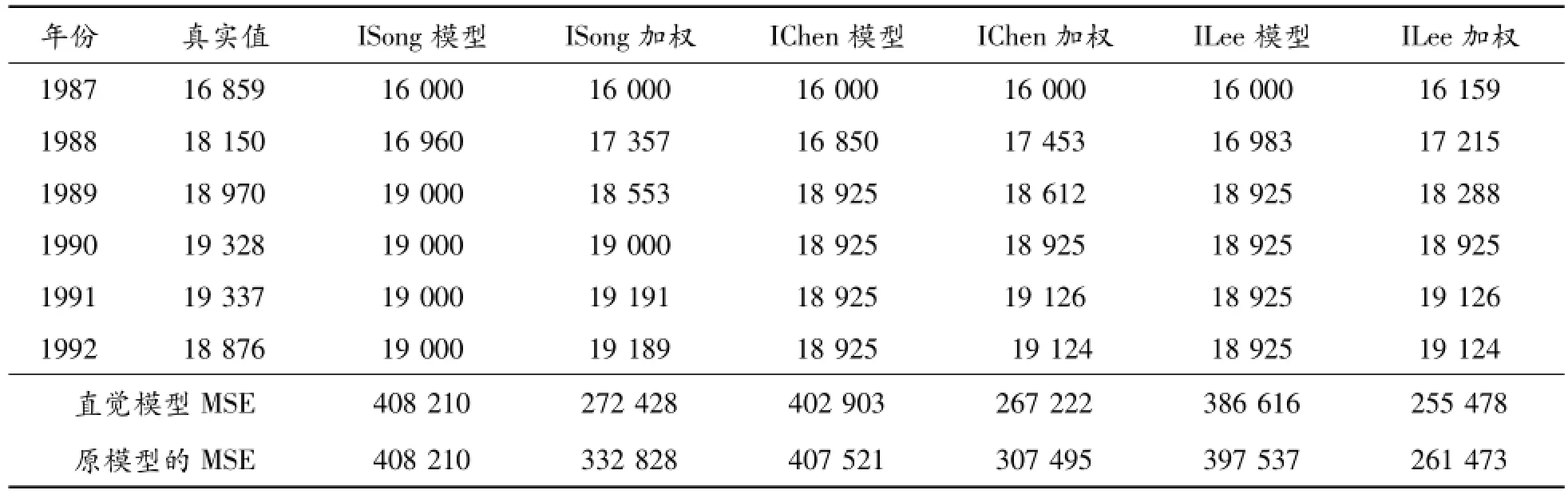
续表（表1）

如图1所示，将本文建立的IFTS模型与对应Song、Chen和Lee模型及其加权模型进行比较，并利用度量标准中的均方误差（MSE）对模型的预测性能进行测试。由表1和图1分析可以看出：本文建立的IFTS模型的预测结果比相对应Song、Chen和Lee模型及其加权模型的预测结果更接近真实值，只有直觉模糊Song模型在只考虑隶属度最大和非隶属度最小时所得的预测结果和原始Song模型的预测结果相同。这是因为在预测过程中仅仅利用了观测值隶属于某个模糊概念的位置，并没有用到观测值隶属于某个模糊概念的隶属度和非隶属度；并且在相对应的IFTS模型中，加权直觉模糊时间序列模型的预测值更贴近真实值，进一步验证了加权直觉模糊模型的优越性。因此，本文建立的IFTS模型通过样本数据直觉模糊化，较好地反映了实际数据的不确定性本质，通过在模糊逻辑关系中引入犹豫度因子充分考虑了样本数据的模糊变化趋势，更加细腻地描述了模糊现象的本质，使模型的预测精度得到进一步提升，验证了本文建立IFTS模型的可行性和可靠性。

图1 直觉模糊模型预测结果对比

4 结束语

本文分析了传统FTS模型局限性，引入直觉模糊集对传统的FTS模型进行扩展。通过样本数据直觉模糊化，较好地反映了实际数据的不确定性本质；在模糊逻辑关系中引入犹豫度因子，充分考虑了样本数据的模糊变化趋势，更加细腻地描述了模糊现象的本质。最后，通过实例验证和对比分析，验证了直觉模糊时间序列模型较好的预测性能。但是，本文犹豫度k的选取过于主观，实际分析中犹豫度的取值会随着样本数据的变化而不同，这也将是今后研究的重点。

［1］ SONG Q，CHISSOM B S.Fuzzy time series and its models［J］.Fuzzy Sets Syst，1993，54：269－277.

［2］ SONG Q，CHISSOM B S.Forecasting enrollments with fuzzy time series-Part I［J］.Fuzzy Sets Syst，1993，54：1－10.

［3］ SONG Q，CHISSOM B S.Forecasting enrollments with fuzzy time series-Part II［J］.Fuzzy Sets Syst，1993，52：1－8.

［4］ ATANASSOV K.Intuitionistic fuzzy sets［J］.Fuzzy Sets and Systems，1986，20（1）：87－96.

［5］ CASTILLO O，ALANISA，GARCIAM，etal.An intuitionistic fuzzy system for times series analysis in plant monitoring and diagnosis［J］.Applied Soft Computing，2007，7（4）：1227－1233.

［6］ 黎昌珍，李瑞岚.基于直觉模糊时变时间序列的预测方法［J］.系统工程，2013，31（3）：100－104.

［7］ 郑窛全，雷英杰，王睿，等.基于确定性转换的IFTS预测［J］.应用科学学报，2013，31（2）：204－211.

［8］ CHEN SM.Forecasting enrollments based on fuzzy time series［J］.Fuzzy Set and Systems，1996，81：311－319.

［9］ LEEM H，EFENDIR，ISMAIL Z.Modified weighted for enrollment forecasting based on fuzzy time series［J］.MATEMATIKA，2009，25（1）：67－78.

［10］郑寇全，雷英杰，王睿，等.直觉模糊时间序列建模及应用［J］.控制与决策，2013（10）：1525－1530.

［11］郑寇全，雷英杰，余晓东，等.基于直觉模糊线性方程组的IFTS预测方法［J］.控制与决策，2014（5）：941－945.

［12］邱望仁.模糊时间序列模型理论及应用研究［M］.天津：天津大学出版社，2012.

（责任编辑陈 艳）

Intuitionistic Fuzzy Tim e Series

TIAN Zong-hao，WANG Peng

（Army Officer Academy，Hefei230031，China）

As to the limitations when dealing with sample data in the fuzzy time series models，this paper introduces intuitionistic fuzzy set theory to obscure time series models.First of all，it obscures the sample data intuitionistic，and reflects the uncertainty nature of the actual data.Then，the hesitation degree factor is developed for the intuitionistic fuzzy logic relationship，and the uncertainty of state transition is described more realistically.Using Song，Chen and Lee’s model as framework，it constructs intuitionistic fuzzy time series forecasting model.Using the enrollment of Alabama for experimental data，it is verified that the intuitionistic fuzzy time series model is more feasible and superior to the model proposed by Song，Chen and Lee.

intuitionistic fuzzy set；fuzzy time series；fuzzy logical relationship；mean squared error

O29

A

1674－8425（2016）12－0177－08

10.3969／j.issn.1674－8425（z）.2016.12.028

2016－07－18

安徽省自然科学基金资助项目（1508085MF131）

田宗浩（1991—），男，河北晋州人，硕士研究生，主要从事预测与决策分析研究，E-mail：1109180769＠qq.com。

田宗浩，王鹏.直觉模糊时间序列［J］.重庆理工大学学报（自然科学），2016（12）：177－184.

format：TIAN Zong-hao，WANG Peng.Intuitionistic Fuzzy Time Series［J］.Journal of Chongqing University of Technology（Natural Science），2016（12）：177－184.