基于RBF神经网络模型的板料成形变压边力优化

谢延敏， 何育军， 田 银

（西南交通大学先进设计与制造技术研究所，四川成都610031）

基于RBF神经网络模型的板料成形变压边力优化

谢延敏， 何育军， 田 银

（西南交通大学先进设计与制造技术研究所，四川成都610031）

为了解决变压边力优化过程中RBF（radial basis function）神经网络隐层节点训练难的问题，利用人工智能算法的优越性，建立了基于人工免疫算法的RBF神经网络，并将其用于非线性函数的逼近中．结合分块压边圈与改变压边力控制技术，通过Dynaform软件进行数值模拟获得成形数据，建立了变压边力与成形质量之间的RBF神经网络近似模型．利用人工免疫智能算法对该近似模型进行优化，获得最优压边力参数．将该方法应用于S形梁冲压成形中，与优化前的结果进行比较，采用优化后最优变压边力可以抑制起皱，最大起皱量减少了89．53%．

板料成形；变压边力；数值模拟；RBF神经网络

板料拉深成形过程中，影响成形质量的因素有很多，如成形件尺寸和形状、压边力大小、板料力学性能、模具结构、摩擦等，在这些影响因素中，控制压边力大小对提高板料冲压成形质量最为明显［1］．

目前，关于压边力大小的确定主要依靠原始经验，缺乏较准确的理论依据和计算．传统的压力机在冲压过程中，压边力不能随冲头行程、冲压时间或冲压位置而变化，制约了板料成形质量的提高．为此，文献［2］中对材料为钛合金的覆盖件施加不同形式的压边力进行研究，试验发现递减型的变压边力不仅能较好的控制材料流入凹模的速度，而且有利于改善材料与凸模型面的贴合状态，获得的覆盖件成形质量也较为理想．文献［3］在单动压力机上，利用计算机技术和多点液压拉深垫系统，建立了一种压边力随时间和位置变化的变压边力控制系统．文献［4］中基于M-K成形极限理论，研究了压边力随时间变化对铝合金成形极限的影响，实验和数值模拟结果均表明变压边力可以显著改善铝合金板成形质量．文献［5］中采用分块压边圈对矩形件进行拉深研究，结果表明，直边区应加载较大的压边力，圆角部位取仅能维持不起皱的较小压边力即可．文献［6］中利用响应面模型和遗传算法进行拉延筋几何参数的优化，结果表明，近似建模技术不仅预测精度和建模效率高，而且可以用于板料成形参数优化．文献［7］中建立了工艺参数与回弹量之间的神经网络模型，并将其应用到某拖拉机后壁板冲压件的工艺参数优化中．文献［8］中将灰色理论和GA-BP结合，建立了多目标神经网络模型，对某汽车车身后纵梁冲压件的工艺参数进行迭代寻优．

目前在板料成形过程中，针对压边力的控制主要包括两个方面：一是压料面的形状和位置的设置，主要体现在拉深筋上；二是压边力大小的选定．由于压料面的形式和位置与具体的成形件形状有关，压边力加载形式和大小的控制相对来说应用普遍，符合板料成形压边力相关理论．本文采用RBF（radial basis function）神经网络对变压边力加载大小与形式进行研究．

1 人工免疫算法与RBF神经网络

人工免疫算法是受自然免疫系统启发而发展起来的一种进化算法．该算法将被求解的问题视为抗原，将问题的解视为抗体．抗体与抗原的匹配程度表现为它们之间的亲合力，抗体之间的亲和力表现为抗体间的相似程度［9-11］．

RBF神经网络是一种具有单隐含层的前向神经网络，利用局部逼近的方法，具有训练速度快、结构简单、泛化性能好等优点，RBF神经网络结构如图1所示．

图1中：n为输入样本数；m为隐节点数；q为输出节点数．

图1 RBF神经网络结构Fig．1 Structure of RBF neural network

RBF网络由3个部分构成：输入层节点（f11，f12，…，f1n）、隐含层节点（f21，f22，…，f2m）和输出层节点（f31，f32，…，f3q）．输入（xk）与输出（ykj）关系为［11-12］

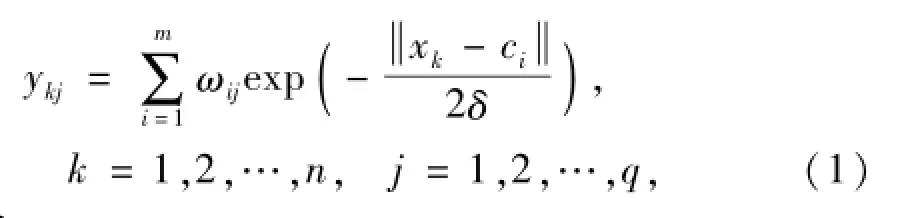
式中：

ωij为隐含层与输出层的连接权值；

ci为第i个隐节点数据中心；

δ为隐含层节点宽度．

RBF神经网络的训练样本集［11］为

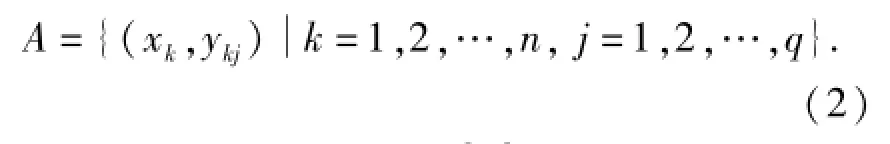
训练样本集的误差函数［11］为

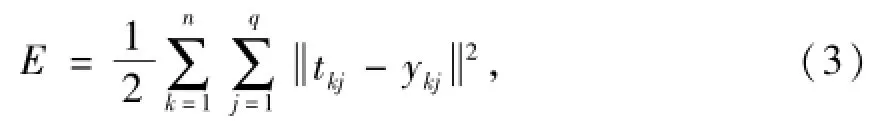
式中：

tkj为与第k组训练数据输入对应第j个神经元的实际输出；

ykj为与第k组训练数据输入对应第j个神经元的期望输出．

2 基于免疫算法的RBF神经网络

2．1 参数定义

由RBF神经网络的原理可知，隐含层主要采用高斯函数作为传递函数．高斯函数是一个关于中心点径向对称的非线性函数，对输入信号产生局部响应，它随着输入与该中心之间的距离增大，函数值迅速衰减到0［11］．

基于此，结合人工免疫算法的特点，假定输入数据xk＝（xk1，xk2，…，xkp）为抗原（p为变量个数），隐含层中第i个中心ci＝（ci1，ci2，…，cip）为抗体，抗原与抗体亲和力［11］为

隐含层数据中心ci1与数据中ci2之间的相似度为

2．2 基于免疫算法的RBF神经网络流程

以人工免疫算法作为RBF神经网络训练方法，获得较优的数据中心和宽度参数，由伪逆矩阵法求得隐含层与输出层的连接权值，整个RBF神经网络训练完毕，具体训练流程如图2所示．

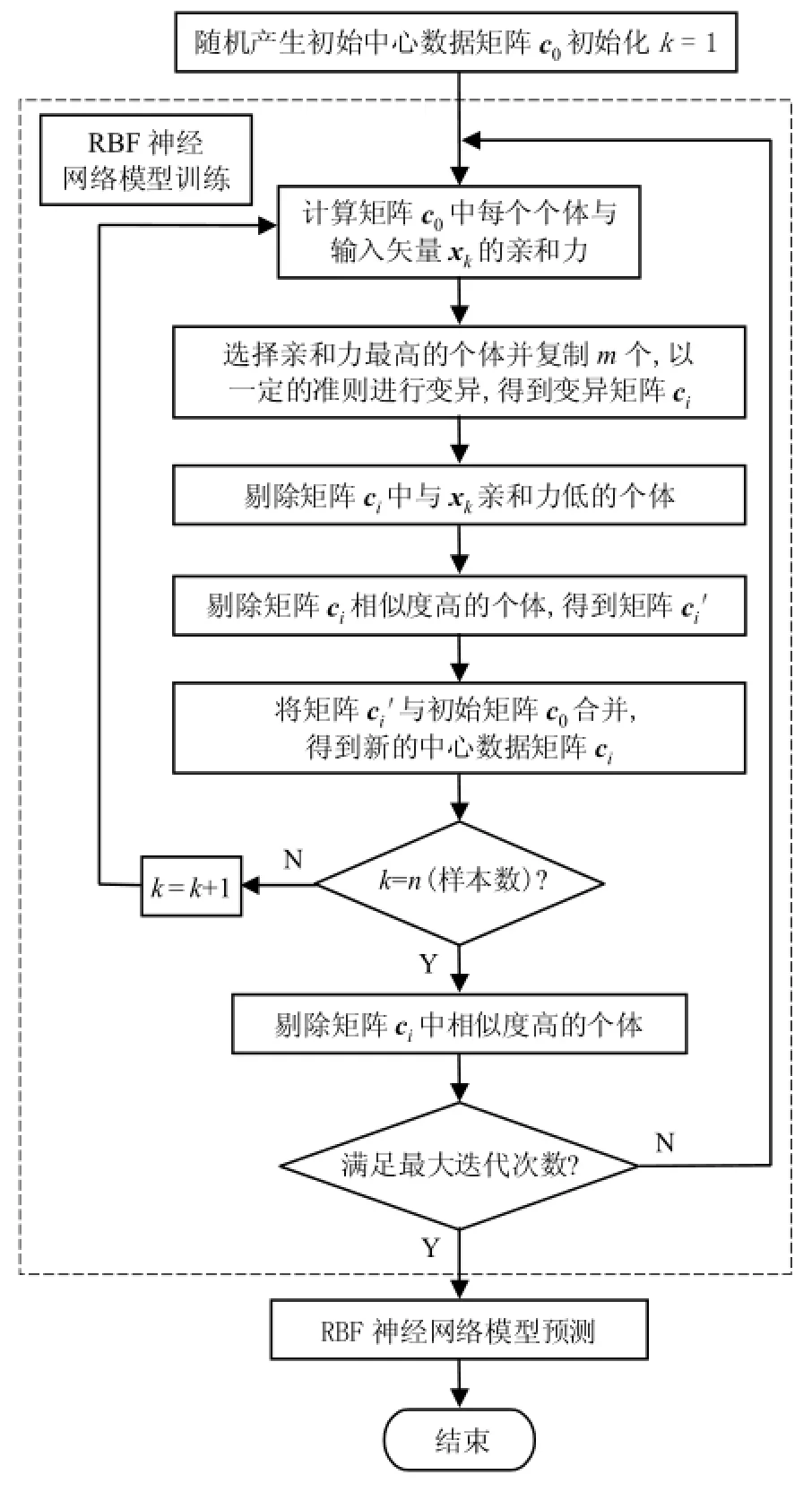
图2 基于人工免疫算法的RBF神经网络训练流程Fig．2 Flow chart of training RBF neural network based on the artificial immune algorithm

2．3 人工免疫训练算法有效性验证

为了检验人工免疫算法作为训练方法训练RBF神经网络效果，用式（6）进行测试，

在［－4，4］之间随机抽取50个样本作为输入，其相对应的函数值作为训练输出，分别采用人工免疫算法和k-均值聚类对RBF神经网络进行训练，再以0．16为步长，在［－4，4］均匀取点作为模型的预测输入样本，其相对应的函数值作为实际输出．在该模型中，径向基函数采用高斯函数，初始RBF神经网络隐含层节点设置为10个，预测结果如图3～5所示．

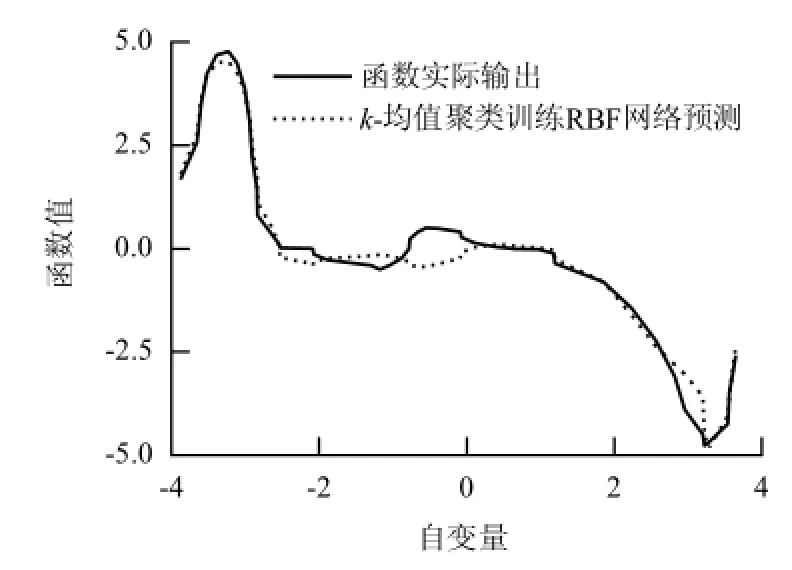
图3 基于k-均值聚类的RBF神经网络预测结果Fig．3 Prediction results of RBF neural network based on k-means clustering

图4 基于人工免疫训练算法的RBF神经网络预测结果Fig．4 Prediction results of RBF neural network based on artificial immune algorithm

对比上述非线性函数的预测结果可以看出，在训练RBF神经网络精度上，人工免疫算法比k-均值聚类更加准确．

由图5可知，k-均值聚类的RBF神经网络预测最大误差为0．939 5，人工免疫训练算法的RBF神经网络最大误差为0．505 0，人工免疫训练算法优势明显．

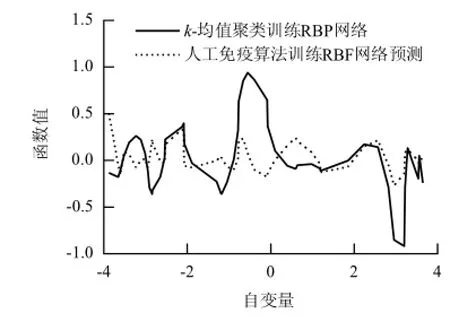
图5 不同训练方法下RBF神经网络预测结果误差Fig．5 Prediction errors of RBF neural network under two different training methods

3 基于免疫算法的RBF神经网络在板料成形中的应用

3．1 S梁冲压成形有限元模型

本文以NUMISHEET'96［13］标准考题S梁为研究对象，采用Dynaform作为仿真软件，凸模、板料、压边圈和凹模的有限元模型如图6所示．

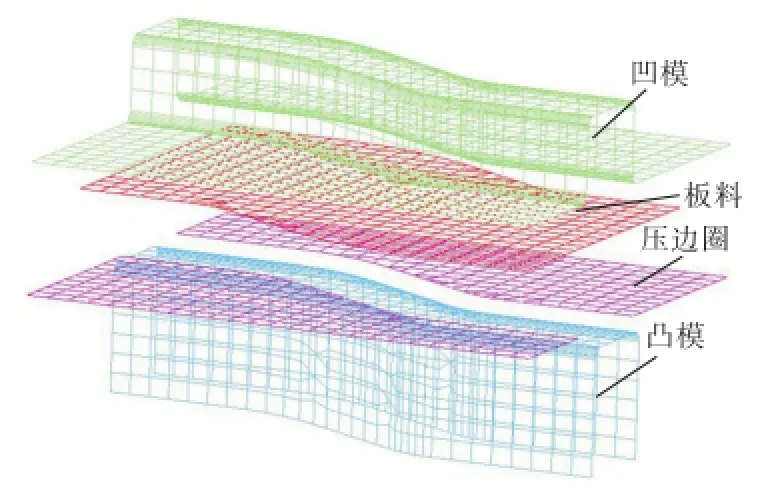
图6 S梁有限元分析模型Fig．6 Finite element analysis model of S-rail

参照文献［13］，材料参数分别为：弹性模量为69 GPa；泊松比为0．33；厚向异性系数为0．64；屈服应力为155 MPa；摩擦因数为0．1；板料厚度为0．92 mm；应力（σ）与应变（εp）关系为

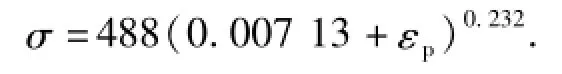
3．2 S梁有限元模型验证

参照文献［14］，在S梁成形试验中，选取B′G′截面线方向作为参考，以回弹后该方向上的高度为测量指标，如图7所示．

采用单动拉深成形，选择四边形BT壳单元，冲压速度设置为4 000 mm／s，数值模拟与实验数据对比如图8所示．

由图8可以看出，仿真结果与实验结果基本一致，说明有限元仿真可以代替物理实验进行后续相关研究．

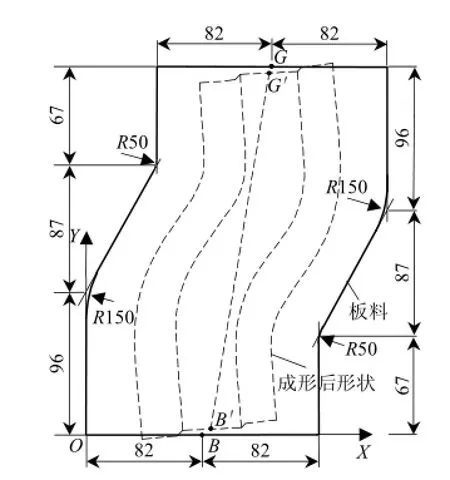
图7 参考截面的位置Fig．7 Location of the reference section

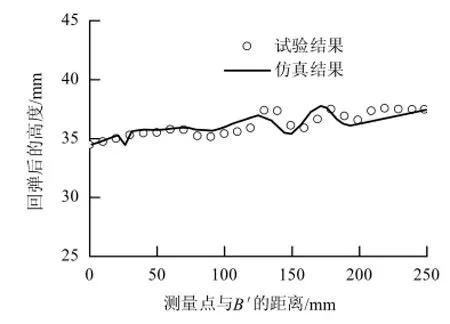
图8 数值模拟和实验结果对比Fig．8 Comparison between the simulations and the experiment data for S-rail

3．3 设计变量与成形质量目标

S梁零件是一种典型的复杂件，具有不对称性，工艺参数若控制不合理，很容易产生破裂和起皱，甚至出现由于零件各部位变形不一致所导致的回弹．针对这一问题，采用中心对称原理，将S梁压边圈划分为3个部分，形成中心对称分块压边，有限元模型如图9所示．

将冲压时间分成4段，每一块压边圈上有4个压边力和2个中间冲压时间转变时刻，共6个输入变量组成，整个模型由18输入变量构成．在每一块压边圈上依次用直线连接构成压边力加载轨迹，整个模型选取最大减薄和最大增厚作为成形目标，其它工艺参数采用文献［14］中的试验值．

在恒定加载条件下，依照既不起皱又不拉裂原则，结合近似模型精度要求，选取压边力取值范围为100～160 kN．表1为18个成形变量取值范围．图10为随时间（t）变压边力（F）加载轨迹．

图9 S梁分块压边圈有限元模型Fig．9 Finite element model of S-rail with block binders

表1 变量取值范围Tab．1 Range of the variables

图10 随时间变压边力加载轨迹Fig．10 Load pathway of blank holder force with time

3．4 基于Dynaform的数值模拟与RBF神经网络模型的建立

通过拉丁超立方抽取50个样本，依次输入Dynaform软件进行仿真，根据仿真结果，分别计算出每次S梁成形质量指标．

将样本输入数据进行归一化处理，前42个样本用来训练，后8个样本用来预测，采用本文中的人工免疫算法训练RBF神经网络．

表2为人工免疫算法训练下的RBF神经网络8个测试样本预测结果．由表2可知，基于人工免疫算法的RBF神经网络模型预测精度比较高，满足建模要求．

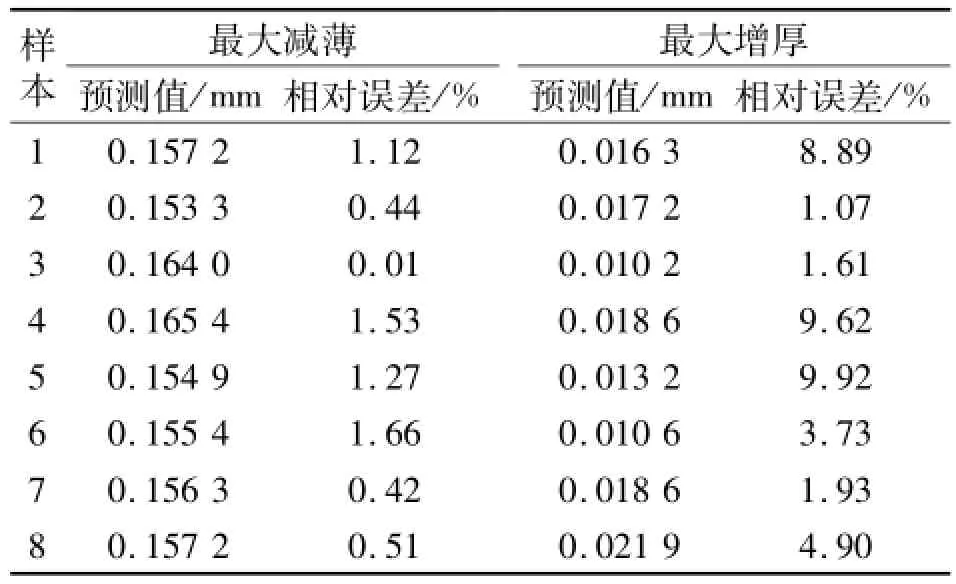
表2 基于人工免疫算法的RBF神经网络预测结果Tab．2 Prediction results of RBF neural network based on artificial immune algorithm

3．5 变压边力的优化与比较

以最大减薄和最大增厚为质量指标，使用人工免疫算法对模型进行优化，经过反归一化处理后，得到：

第1块压边圈上变压边力为

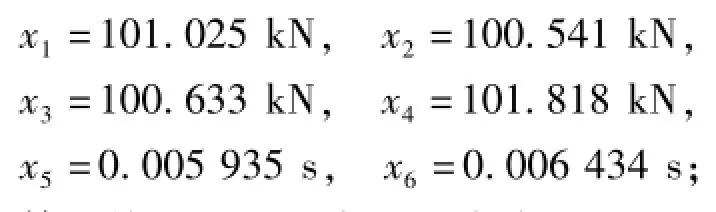
第2块压边圈上变压边力为

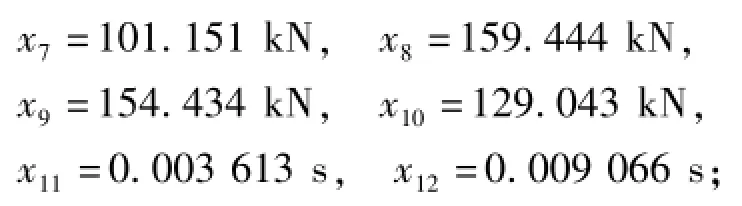
第3块压边圈上变压边力为

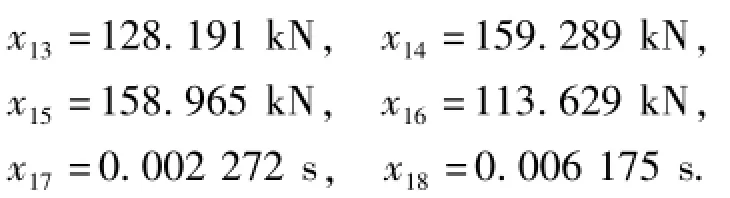
与之对应的成形目标最大减薄值为0．154 mm，最大增厚值为0．008 mm．

图11～13分别为3块压边圈最优变压边力加载轨迹曲线．

为了验证上述优化结果的准确性，将优化所得的最优工艺参数值输入S梁有限元模型，计算仿真结果最大减薄值为0．161 mm，最大增厚值为0．009 mm，与优化结果基本一致．同时利用文献［14］中试验数据进行仿真，求得最大减薄值为0．089 mm，最大增厚值为0．086 mm．在安全余量范围内，最大起皱量减少了89．53%．

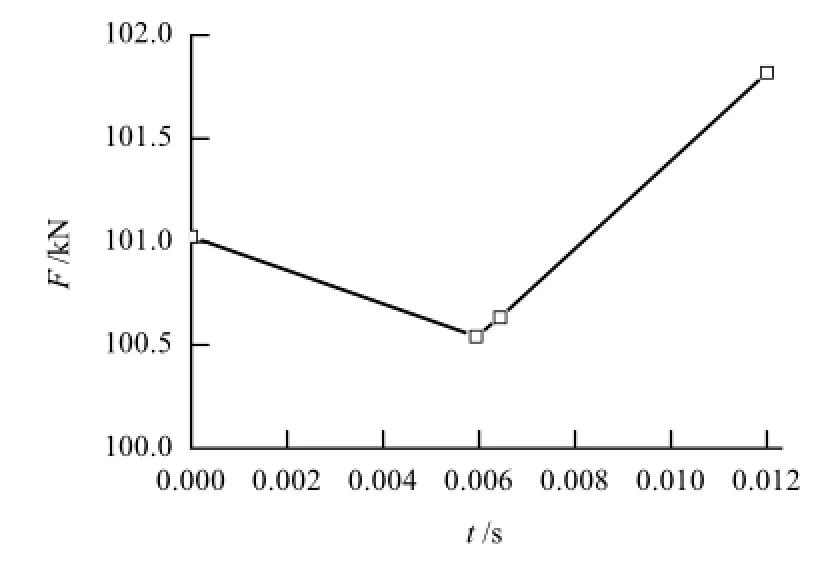
图11 压边圈1变压边力加载轨迹Fig．11 Load pathway of blank holder force for block 1

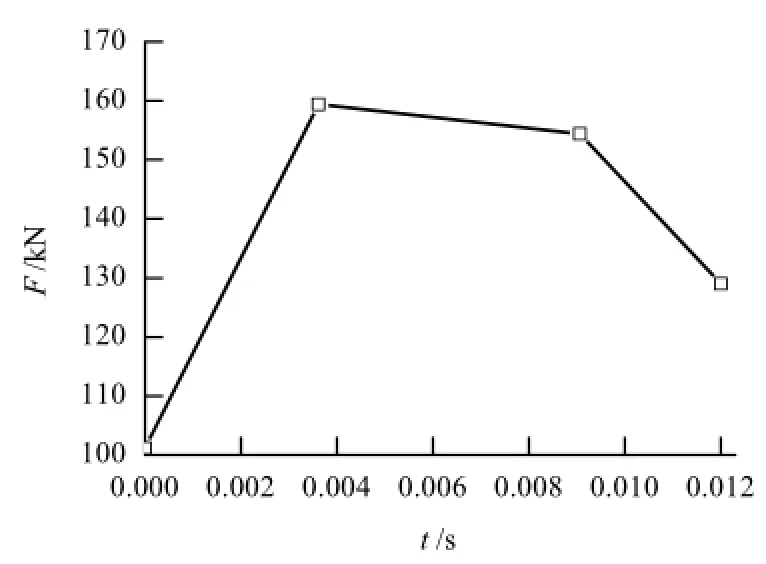
图12 压边圈2变压边力加载轨迹Fig．12 Load pathway of blank holder force for block 2

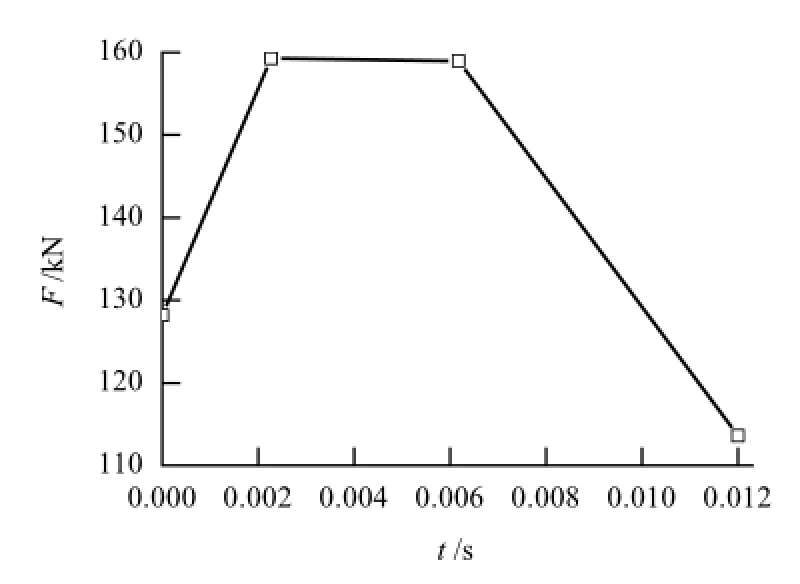
图13 压边圈3变压边力加载轨迹Fig．13 Load pathway of blank holder force for block 3

S梁成形优化前与优化后FLD对比如图14、15所示．

结果表明，采用优化后的最优变压边力，起皱得到了较好的抑制，S梁成形质量得到了极大提高．

图14 优化前S梁的FLD图Fig．14 Forming limit diagram of S-rail before optimization

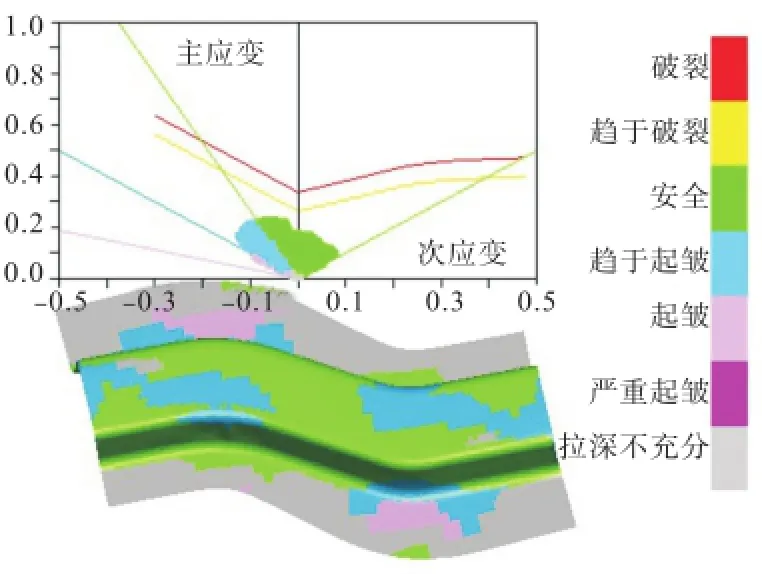
图15 优化后S梁的FLD图Fig．15 Forming limit diagram of S-rail after optimization

4 结 论

本文将分块压边与变压边力技术相结合，借助RBF神经网络近似模型，研究了变压边力优化，得到如下结论：

（1）利用人工免疫算法和RBF神经网络建立了分块随时间变化的变压边力与成形质量的映射模型．通过对该模型进行优化，获得了最优变压边力；

（2）通过与传统整体压边成形效果相对比，将该方法获得的最优变压边力应用到板料成形中，最大起皱量减少了89．53%，提高了板料成形质量；

（3）通过对某非线性函数的预测结果可以看出，在训练RBF神经网络精度上，人工免疫算法比k-均值聚类更加准确．

［1］ 李少平，郑静风，何丹农．板料成形参数对拉深成形性能影响的正交分析［J］．锻压技术，2002，27（3）：27-28．LI Shaoping，ZHENG Jingqiu，HE Dannong．Orthogonal analysis of influence of sheet forming parameters on drawing properties［J］．Forging＆Stamping Technology，2002，27（3）：27-28．

［2］ KAZUNARI K，MASAHIRO S，YASUO H，et al．Binding force control of uni-pressure cushion in automobile panel stamping［C］∥1995 SAE International Congress and Exposition．Detroit：［s．n．］，1995：No．950916．

［3］ SIEGERT K，DANNEMANN E，WAGNER S，et al．Closed-loop control system for blank holder forces in deep drawing［J］．Ann CIRP，1995，44（1）：251-254．

［4］ 陈关龙，孙成智，王东川，等．变压边力对铝合金板冲压成形的影响研究［J］．塑性工程学报，2005，12（3）：41-45．CHEN Guanlong，SUN Chenzhi，WANG Dongchuan，et al．Mechanism investigation of variable blank-holder forces improving the formability of aluminum alloy sheets during sheet metal forming［J］．Journal of Plasticity Engineering，2005，12（3）：41-45．

［5］ 孙成智，陈关龙，李淑慧，等．变压边力对矩形件成形性能的影响［J］．塑性工程学报，2003，10（4）：1226-1229．SUN Chengzhi，CHEN Guanlong，LI Shuhui，et al．The effect of variable blank-holder forces on formability of ractangle box deep drawing［J］．Journal of Plasticity Engineering，2003，10（4）：1226-1229．

［6］ 郑刚，李光耀，孙光永，等．基于近似模型的拉延筋几何参数反求［J］．中国机械工程，2006，17（19）：1988-1992．ZHENG Gang，LI Guangyao，SUN Guangyong，et al．Geometrical parameter inverse problem for drawbeads based on the approximate model［J］．China Mechanical Engineering，2006，17（19）：1988-1992．

［7］ 苏娟华，张文琼，李丽春．神经网络与正交试验法结合优化板料成形工艺［J］．锻压技术，2009，33（1）：154-156．SU Juanhua，ZHANG Wenqiong，LI Lichun． Application of network and orthgonal experiment method in optimization of sheet metal forming process technology［J］．Forging＆Stamping Technology，2009，33（1）：154-156．

［8］ 周杰，华俊杰，阳德森，等．基于GS理论与GA-BP网络的板料多目标成形工艺优化［J］．热加工工艺，2009，38（17）：73-76．ZHOU Jie，HUA Junjie，YANG Desen，et al．Optimization of forming process for sheet metal multiobjective based on GS theory and GA-BP network［J］．Hot Working Process，2009，38（17）：73-76．

［9］ 焦李成，杜海峰，刘芳，等．免疫优化计算、学习与识别［M］．北京，科学出版社，2006：53-92．

［10］ 郑日荣．基于欧式距离和精英交叉的免疫算法研究［D］．广州：华南理工大学，2004．

［11］ 田银，谢延敏，孙新强，等．基于鱼群RBF神经网络和改进蚁群算法的拉深成形工艺参数优化［J］．锻压技术，2014，39（12）：129-136．TIAN Yin，XIE Yanmin，SUN Xinqiang，et al．Process parameters optimization of deep drawing based on fish RBF neural network and improved ant colony algorithm［J］．Forging＆Stamping Technology，2014，39（12）：129-136．

［12］ 谢延敏，田银，孙新强，等．基于灰色关联的铝合金板拉深成形扭曲回弹工艺参数优化［J］．锻压技术，2015，40（3）：25-31．XIE Yanmin，TIAN Yin，SUN Xinqiang，et al．Optimization of twist springback process parameters of aluminum alloy aheet forming based on grey correlation［J］．Forging＆Stamping Technology，2015，40（3）：25-31．

［13］ SCHWARZE M，VLADIMIROV IN，REESE S．Sheet metal forming and springback simulation by means of a new reduced integration solid-shell finite element technology［J］．Computer Methods in Applied Mechanics and Engineering，2011，200（5／6／7／8）：454-476．

［14］ LEE S W，YOON J W，YANG D Y．Comparative investigation into the dynamic explicit and the static implicit method for springback of sheet metal stamping［J］．Engineering Computations，1999，16（3）：347-373．

（中文编辑：秦 瑜 英文编辑：兰俊思）

Optimization of Variable Blank Holder Forces in Sheet Metal Forming Based on RBF Neural Network Model

XIE Yanmin， HE Yujun， TIAN Yin
（Institute of Advanced Design and Manufacturing，Southwest Jiaotong University，Chengdu 610031，China）

In order to solve the difficulty of training the hidden layer nodes in radial basis function（RBF）neural network during the optimization of variable blank holder forces，a RBF neural network based on the artificial immune algorithm was established by taking advantages of artificial intelligence algorithms，and then used to approximate a nonlinear function．Using both the block blank holder technology and the variable blank holder force control technology，numerical simulations were conducted in Dynaform to obtain the forming data，and an approximate model of RBF neural network was established between the variable blank holder forces and the forming quality．The approximate model was optimized by artificial immune algorithm to obtain the optimal blank holder force parameters．In addition，the method was applied to the S-rail stamping．The results show that compared with that before optimization，the maximum wrinkle amount was reduced by 89．53%，and wrinkles could be effectively controlled by the optimized variable blank holder forces．

sheet forming；variable blank holder force；numerical simulation；RBF neural network

TG386

A

0258-2724（2016）01-0121-07

10．3969／j．issn．0258-2724．2016．01．018

2015-06-16

国家自然科学基金资助项目（51275431）

谢延敏（1975—），男，副教授，博士，研究方向为先进塑性加工技术仿真和稳健设计，E-mail：xie_yanmin＠swjtu．edu．cn

谢延敏，何育军，田银．基于RBF神经网络模型的板料成形变压边力优化［J］．西南交通大学学报，2016，51（1）：121-127．