Capacity Analysis on Distributed Antenna System with Imperfect CSI over Rayleigh Fading Channel

, , , ,

Jiangsu Key Laboratory of Internet of Things and Control Technologies, College of Electronic and Information Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, P. R. China



Capacity Analysis on Distributed Antenna System with Imperfect CSI over Rayleigh Fading Channel

WuBinbin,YuXiangbin*,WangYing,LiYang,QiuSainan

Jiangsu Key Laboratory of Internet of Things and Control Technologies, College of Electronic and Information Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, P. R. China

(Received 17 October 2015; revised 26 March 2016; accepted 30 March 2016)

Considering that perfect channel state information (CSI) is hard to obtain in practice, the capacity of downlink distributed antennas system (DAS) with imperfect CSI is analyzed over Rayleigh fading channel. Based on the performance analysis, using the probability density function and numerical calculation, an accurate closed-form expression of ergodic capacity of downlink DAS under imperfect CSI is derived. It includes the one under perfect CSI as a special case. This theoretical expression can provide good performance evaluation for downlink DAS for both perfect and imperfect CSI due to its accuracy. Simulation results indicate that the theoretical analysis agrees well with the corresponding simulation, and the capacity can be increased effectively by decreasing the estimation error and /or path loss.

distributed antenna system; capacity analysis; imperfect CSI; downlink; path loss

0 Introduction

Distributed antenna system (DAS), as a promising technique for next generation wireless mobile communications, has received significent attention thanks to its power efficiency and capacity improvement over traditional co-located antenna system (CAS)[1-2]. Different from conventional CAS, DAS consists of several widely spaced antennas, and each of them is called an antenna port (AP). Through coaxial cables or fiber optics, all the APs are connected to the main processing unit (MPU).

Ergodic capacity, as a measure of the system performance, plays an important role in communication systems. Based on different system models, the capacity of DAS has been extensively studied[3-7]. Ref. [3]analyzed the channel capacity of uplink, but neglected the large-scale fading for convenient analysis. The performance of DAS capacity over a composite fading channel was studied in Refs.[4—7]. Considering selective transmission and maximal ratio combining, using a log-normal distribution instead of the actual gamma-log-normal distribution, approximate expressions of the ergodic capacity were derived for downlink DAS[4-6], where Rayleigh fading channel[5-6]and Nakagami-mfading channel[4]were considered, respectively. However, the derived theoretical capacity formulae are not accurate to reflect the actual value because of the approximate substitution. For high signal-to-noise-ratio (SNR) analysis, Ref.[7] derived a simple ergodic capacity expression, which was close to the actual cell ergodic capacity at high SNR.

According to the analysis above, although the capacity of DAS has been well studied, the performance analyses were based on perfect channel state information (CSI). Whereas in practice, the perfect CSI is difficult to obtain due to channel estimation error. Therefore, we study DAS capacity with imperfect CSI over composite Rayleigh fading channel, where both small-scale fading (Rayleigh fading) and large-scale fading (path loss) are considered. The channel model from imperfect estimation is firstly presented for DAS, and then the probability density function (PDF) and conditional PDF of output SNR are derived by means of Bayesian linear model. With these PDFs, using the numerical calculation, an accurate closed-form ergodic capacity expression of downlink DAS with imperfect CSI is derived. With this expression, the ergodic capacity in the presence of imperfect CSI can be effectively evaluated. Moreover, it includes the capacity expression under perfect CSI as a special case. Simulation results verify the effectiveness of our theoretical analysis.

1 System and Channel Models

We consider a distributed antenna system with multiple APs in a single-cell environment, and the APs are distributed in the cell with radiusRand connected to the main processing unit via dedicated wireless (e.g. fiber option) for signal processing, whereNtAPs are considered, and theith AP is denoted as APi. Considering the implementation of mobile terminal (MT), single receive antenna is available at the MT[5-6]. This is also due to the limitation of volume and size of the MT. The positions of the MT and theith AP are denoted by the polar coordinates (ρ,ν) and (Ri,τi),i=1,…,Nt, respectively, whereρandνare the distance and the angle of the MT to the cell center, respectively.Riandτiare the distance and the angle of theith AP to the cell center, respectively. To improve the performance, the antenna selection technology is employed for APs. If APiis selected to transmit signals, the received signals at MT can be expressed as

(1)

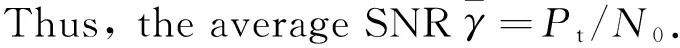
Due to the structural features of DAS,hican be modeled as

(2)

wherekirepresents the small-scale fast fading betweenAPiand MT,Lithe path loss betweenAPiand MT. The envelope of the fast fading is assumed to undergo a Rayleigh fading. The path loss termLican be modeled as

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

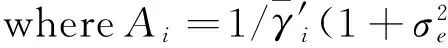
(11)

(12)

(13)

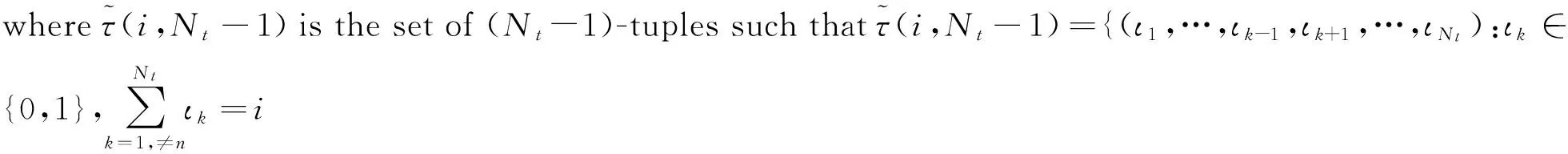
2 Ergodic Capacity Analysis

In this section, we will give the capacity analysis of the DAS with imperfect CSI. The ergodic capacity of the mobile terminal at a given location can be expressed as

(14)

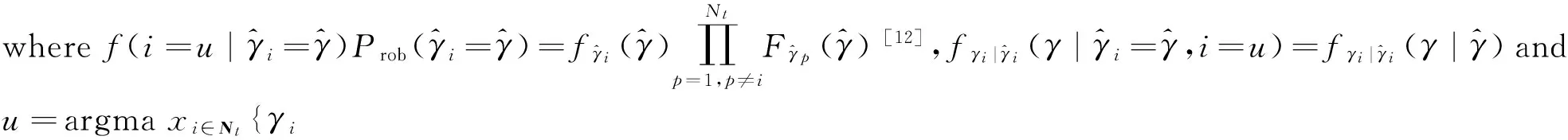
(15)

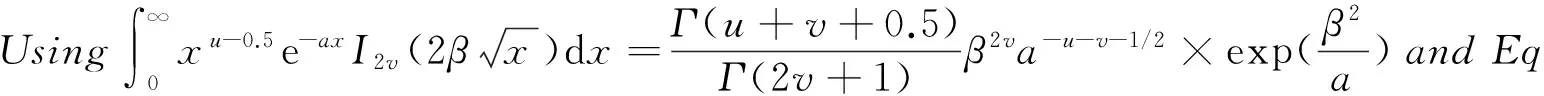
(16)

Substituting Eq.(16) into Eq.(14) yields

(17)

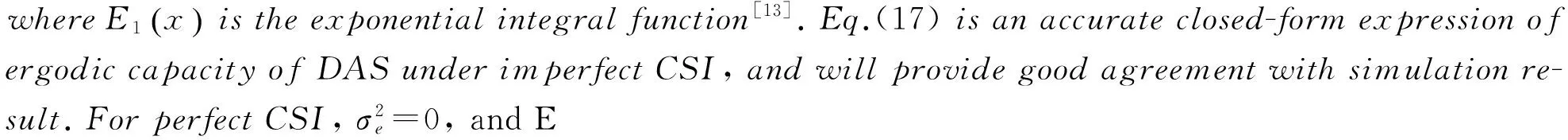
(18)

Eq.(18) is an accurate closed-form expression of ergodic capacity of DAS with perfect CSI, and can match the simulation well. According to this, the derived Eq.(17) includes the ergodic capacity under perfect CSI as a special case.

3 Simulation Results

In this section, we use the derived theoretical formula and simulation results to evaluate the ergodic capacity of DAS with antenna selection under imperfect CSI. In the simulation,NtAPs are evenly and symmetrically placed in the cell, that is, the distances between each AP and the MPU are the same, and the angles between every two neighboring APs are also the same[5-6]. The Monte-Carlo method is employed for simulation and single receive antenna is considered. The simulation results are illustrated in Figs.1—3. The main simulation parameters are listed in Table 1.

Table 1 Simulation parameters of DAS

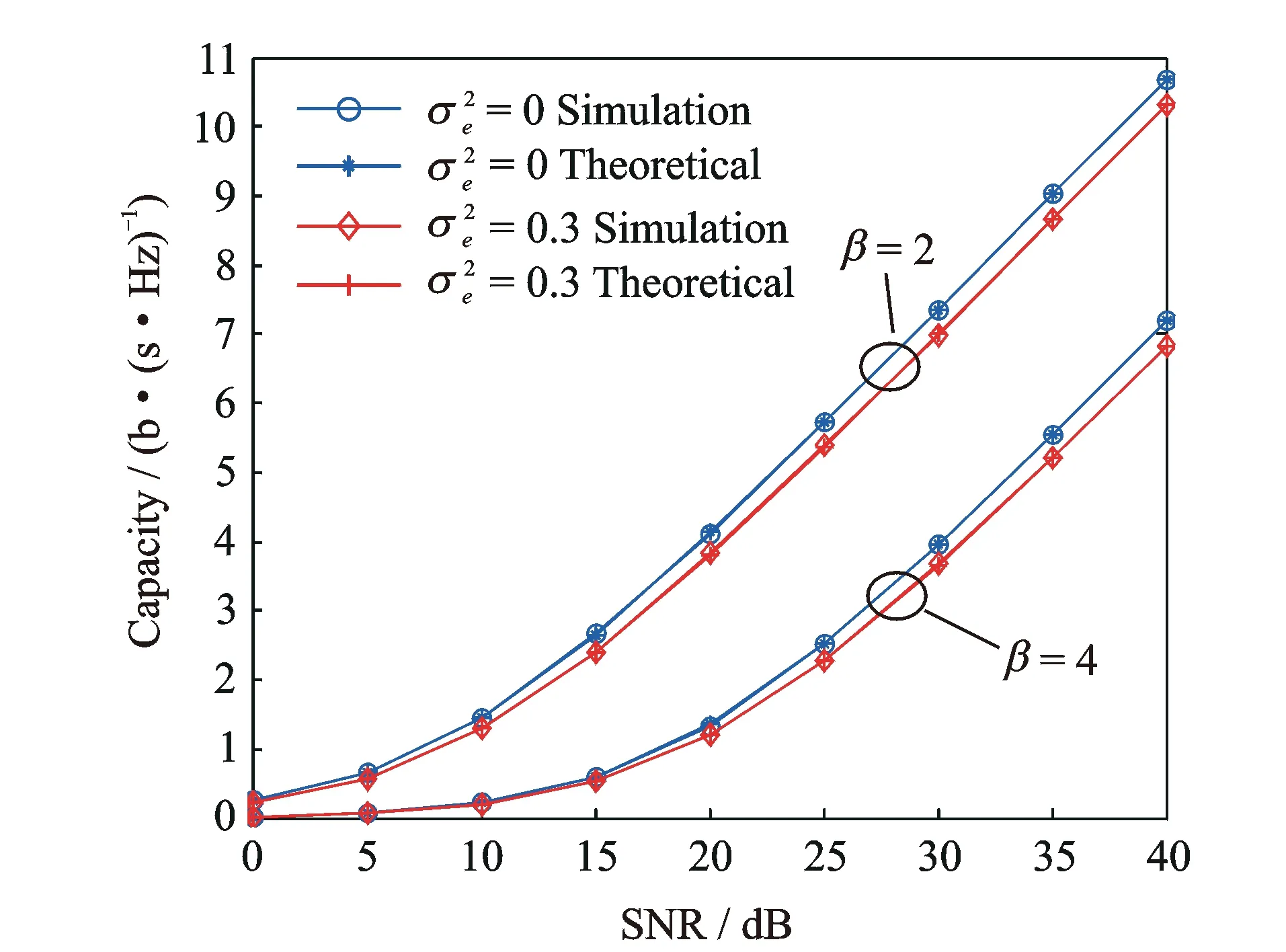
Fig.1 Capacity of DAS with different path loss exponents and estimation errors (Nt=5)

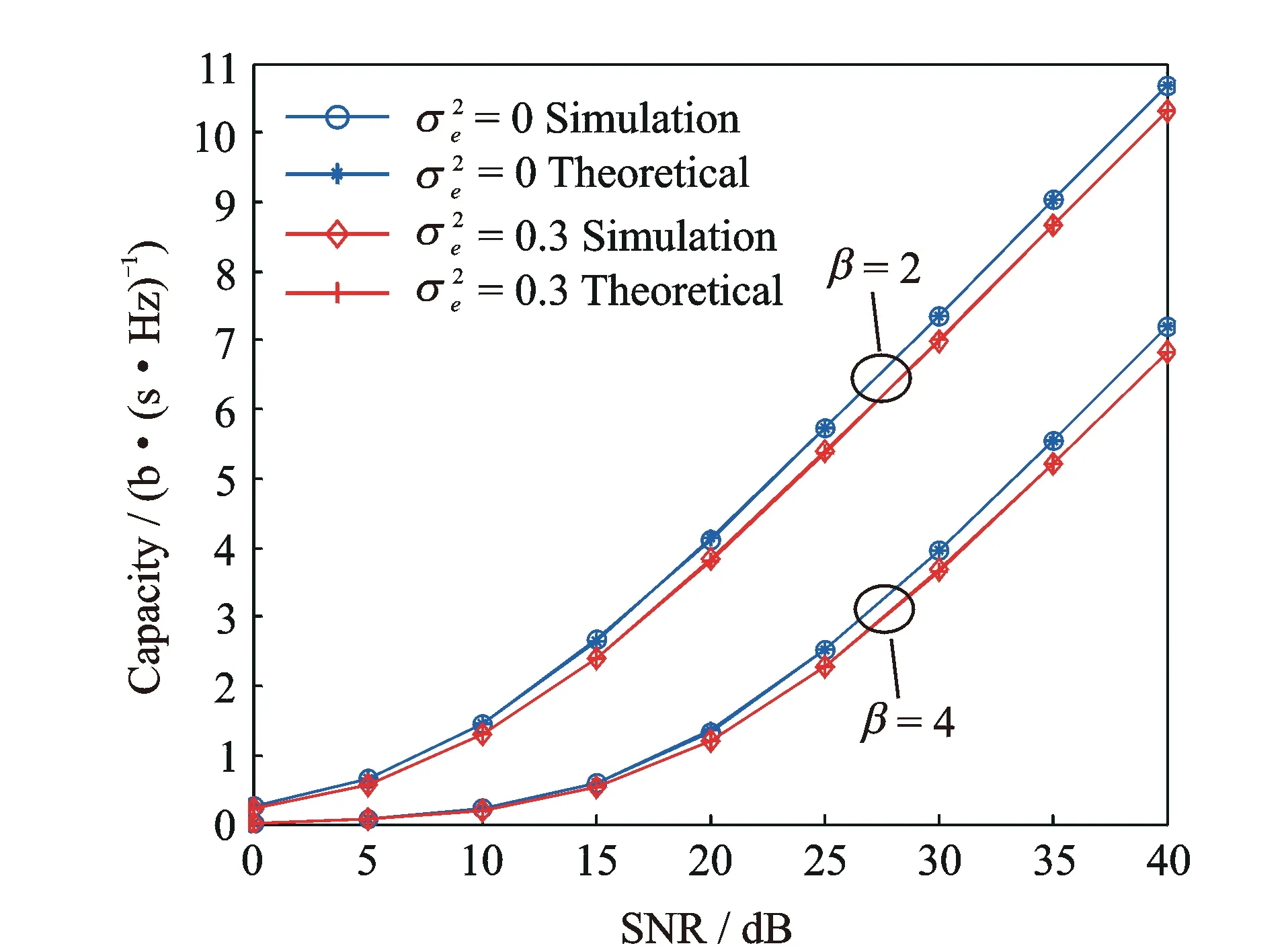
Fig.2 Capacity of DAS with different path loss exponents and estimation errors (Nt=9)

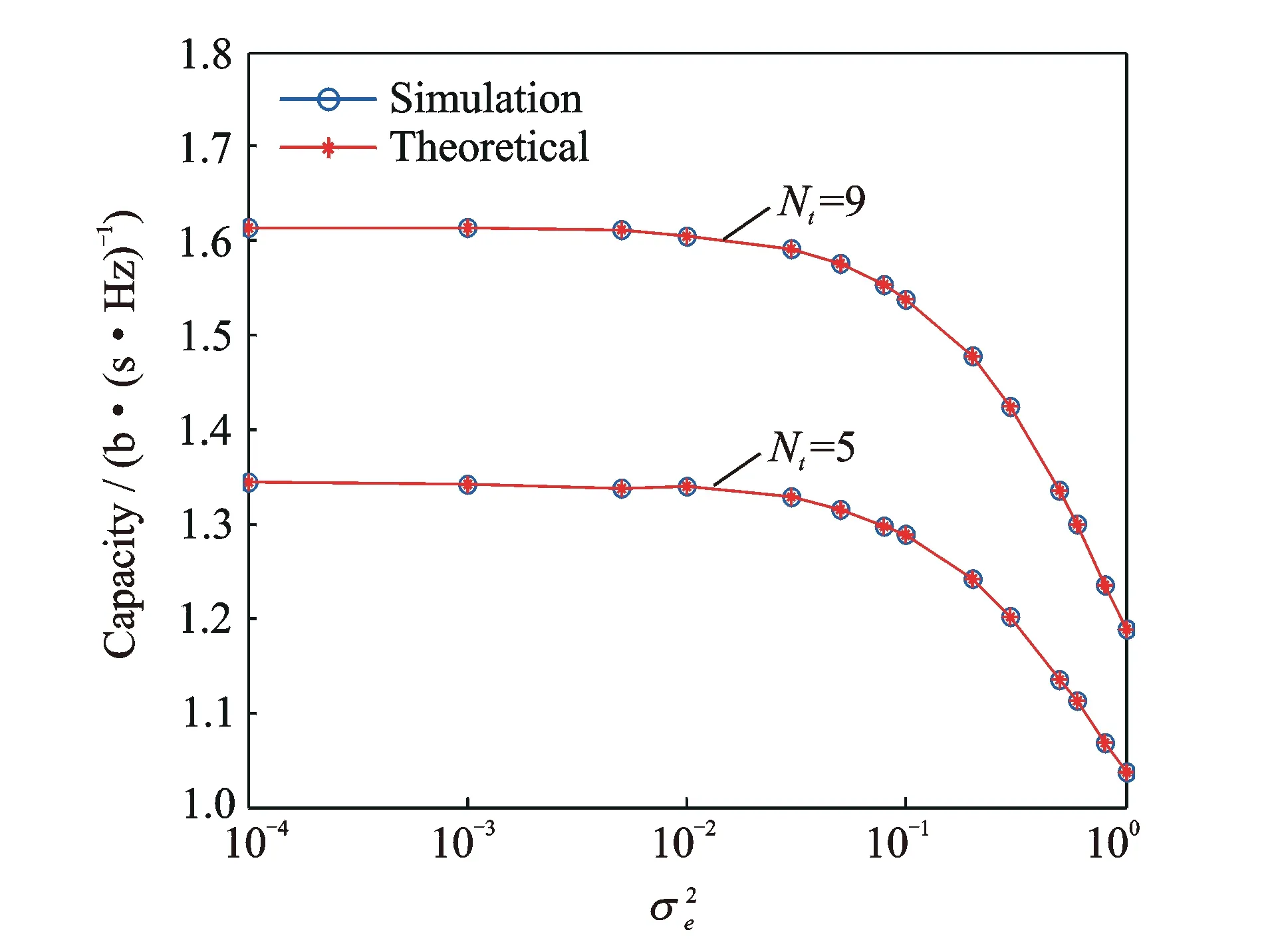
Fig.3 Capacity of DAS with different estimnaton errors and APs

4 Conclusions

We have studied the performance of downlink DAS capacity with imperfect CSI caused by estimation error in composite Rayleigh fading channel. Based on the performance analysis and established channel model, the closed-form PDF and CDF of the estimated SNR are derived, respectively. Using these functions and numerical calculation, an accurate closed-form capacity expression of DAS with single receive antenna under imperfect CSI is obtained. When channel estimation has no error, this expression is reduced to the one under perfect CSI. Using this expression, the capacity of downlink DAS in the presence of perfect and imperfect CSI can be effectively evaluated. The analysis indicates that DAS capacity is insensitive to the estimation error variance smaller than 0.01. Simulation results show that the derived capacity expression can match the corresponding simulation well, and the capacity may be improved by decreasing the estimation error and/or path loss exponent, and /or increasing the number of APs.

Acknowledgements

This work was supported by the Doctoral Fund of Ministry of Education of China (No.20093218120021), the Fundamental Research Funds for the Central Universities, the Research Founding of Graduate Innovation Center in NUAA (Nos.kfjj201429, kfjj20150410), and the PARD of Jiangsu Higher Education Institutions, Qing Lan Project of Jiangsu.

[1] ROBERT H, STEVEN P, YI W. A current perspective on distributed antenna systems for the downlink of cellular systems [J]. IEEE Communications Magazine, 2013, 51(4):161-167.

[2] ZHOU S, ZHAO M, WANG J, et al. Distributed wireless communication systems: A new architecture for future public wireless access [J]. IEEE Communications Magazine, 2003, 41(3):108-113.

[3] DAI L, ZHOU S, YAO Y. Capacity analysis in CDMA distributed antenna systems [J]. IEEE Transactions on Wireless Communications, 2006, 4(6):2613-2620.

[4] CHEN H M, CHEN M. Capacity of the distributed antenna systems over shadowed fading channels [C]∥ IEEE Vehicular Technology Conference. Spain, Barcelona:IEEE, 2009: 1-4.

[5] WANG J Y, WANG J B, DANG X Y, et al. System capacity analysis of downlink distributed antenna systems over composite channels [C] //IEEE International Conference on Communication Technology. Nanjing: IEEE, 2010: 1076-1079.

[6] WANG J B, WANG J Y, CHEN M, et al. Downlink system capacity analysis in distributed antenna systems [J]. Wireless Personal Communications, 2012, 67: 631-645.

[7] LEE S R, MOON S H, KIM J S, et al. Capacity analysis of distributed antenna systems in a composite fading channel [J]. IEEE Transactions on Wireless Communications, 2012, 11(3):1076-1086.

[8] SHI Z, LEIB H. Transmit antenna selected V-BLAST systems with power allocation [J]. IEEE Transaction on Vehicular Technology, 2008, 57(4):2293-2304.

[9] KUANG Q, LEUNG S H, YU X B, et al. Adaptive modulation and joint temporal spatial power allocation for OSTBC MIMO systems with imperfect CSI [J]. IEEE Transaction on Communications, 2012, 60(7):1914-1924.

[10]KAY S M. Fundamentals of statistical signal processing: Estimation theory [M]. New York: Prentice Hall, 1998.

[11]JUAN M, JEREZ R, GOLDSMITH J. Performance of multichannel reception with transmit antenna selection in arbitrarily distributed Nagakami fading channels [J]. IEEE Transactions on Wireless Communication, 2009, 8(4): 2006-2013.

[12]TORABI M, FRIGON J F, BRUNILDE S. Performance analysis of adaptive modulation in multiuser selection diversity systems with OSTBC over time-varying channels [J]. IEEE Signal Processing Letters, 2012, 19(4): 211-214.

[13]GRADSHTEYN I , RYZHIK I. Table of integrals, series, and products [M]. 7th ed. San Diego, CA: Academic, 2007.

Mr.Wu Binbin received his M.S. degree in Communication and Information System from Nanjing University of Aeronautics and Astronautics, Nanjing, China, in 2016. His research focuses on digital communication.

Prof. Yu Xiangbin received his Ph.D. degree in Communication and Information Systems in 2004 from National Mobile Communications Research Laboratory at Southeast University, Nanjing, China. He is a Professor of Information and Communication Engineering at Nanjing University of Aeronautics and Astronautics. His research interests include green communication, adaptive modulation, precoding design and space-time signal processing.

Ms.Wang Ying received the B.S. degree in Information Engineering from Nanjing University of Aeronautics and Astronautics, Nanjing, China, in 2014. She is currently a postgraduate student at Nanjing University of Aeronautics and Astronautics.

Mr.Li Yang received his M.S. degree in Communication and Information System from Nanjing University of Aeronautics and Astronautics, Nanjing, China, in 2016.

Ms.Qiu Sainan received the B.S. degree in information Engineering from Nanjing University of Aeronautics and Astronautics, Nanjing, China, in 2014. She is postgraduate student at Nanjing University of Aeronautics and Astronautics.

(Executive Editor: Zhang Bei)

TN925 Document code:A Article ID:1005-1120(2016)06-0733-06

*Corresponding author, E-mail address: yxbxwy@nuaa.edu.cn. How to cite this article: Wu Binbin, Yu Xiangbin, Wang Ying, et al.Capacity analysis on distributed antenna system with imperfect CSI over Rayleigh fading channel[J]. Trans. Nanjing Univ. Aero. Astro., 2016,33(6):733-738. http://dx.doi.org/10.16356/j.1005-1120.2016.06.733