Construction of Low Delay Maximal Rate Single-Symbol Decodable Distributed STBC with Channel Phase Information

, , ,

1.College of Information Engineering, Yangzhou University, Yangzhou 225127, P.R. China；2.School of Electronic and Optical Engineering, Nanjing University of Science and Technology, Nanjing 210094, P.R. China；3.College of Electronic and Information Engineering，Nanjing University of Aeronautics and Astronautics, Nanjing 210016, P.R. China；4.National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, P.R. China



Construction of Low Delay Maximal Rate Single-Symbol Decodable Distributed STBC with Channel Phase Information

ChenJunsheng1,2*,ZhangXiaofei3,ShuFeng2,4,WangJianxin2

1.College of Information Engineering, Yangzhou University, Yangzhou 225127, P.R. China；2.School of Electronic and Optical Engineering, Nanjing University of Science and Technology, Nanjing 210094, P.R. China；3.College of Electronic and Information Engineering，Nanjing University of Aeronautics and Astronautics, Nanjing 210016, P.R. China；4.National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, P.R. China

(Received 20 November 2015; revised 6 Mach 2016; accepted 28 March 2016)

Exploiting the source-to-relay channel phase information at the relays can increase the rate upper-bound of distributed orthogonal space-time block codes (STBC) from 2/Kto 1/2, whereKis the number of relays. This technique is known as distributed orthogonal space-time block codes with channel phase information (DOSTBC-CPI). However, the decoding delay of existing DOSTBC-CPIs is not optimal. Therefore, based on the rate of 1/2 balanced complex orthogonal design (COD), an algorithm is provided to construct a maximal rate DOSTBC-CPI with only half the decoding delay of existing DOSTBC-CPI. Simulation results show that the proposed method exhibits lower symbol error rate than the existing DOSTBC-CPIs.

distributed STBC; channel phase information; decoding delay; single-symbol decoding

0 Introduction

Distributed space-time block coding is an effective way of implementing cooperative communication systems[1-4]. To find distributed space-time block codes (DSTBC) in the set of complex orthogonal designs (COD) is natural and reasonable. However, the decoding of DSTBC depends on the covariance matrixΓof the equivalent noise at the destination, which will destroy the orthogonality of COD. Therefore, when the COD for point-to-point multiple input multiple output (MIMO) systems are directly applied to cooperative wireless networks, they are usually no longer single-symbol decodable and the decoding complexity grows exponentially with the size of the symbol constellation used[5].

To construct single symbol decodable DSTBCs, Yi et al.[5]proposed distributed row-monomial orthogonal space-time block codes (DOSTBC). The rate of row-monomial DOSTBC is upper-bounded by 2/K, whereKis the number of relays. Although this is twice that of the repetition-based schemes, it is still inversely proportional to the number of relays. To address this issue, Sreedhar et al.[6]and Yi et al.[7]have independently illustrated that exploiting the source-to-relay channel phase information (CPI) at the relays can increase the rate of DOSTBC dramatically from 2/Kto 1/2, and this rate is achievable by the well-known rate-1/2 COD given by Tarokh et al.[8](denoted as TJC code). The DOSTBCs that use CPI are known DOSTBC-CPIs. However, Refs. [9—10] show that the decoding delay of the TJC code is not optimal.

Therefore, based on the balanced COD (BCOD) given in Ref.[10], we propose an algorithm to construct a class of DOSTBC-CPIs that not only retain all the advantages of the TJC code such as maximal rate, full diversity and single-symbol decodable, but also hold only half the decoding delay of the latter. Simulation results show that the proposed design also outperforms TJC code in terms of symbol error rate (SER).

1 System Model

Consider a cooperative wireless network as shown in Fig.1, with one source nodeS, one destination nodeD, andKrelay nodes denoted asRifori=1, 2, …,K.

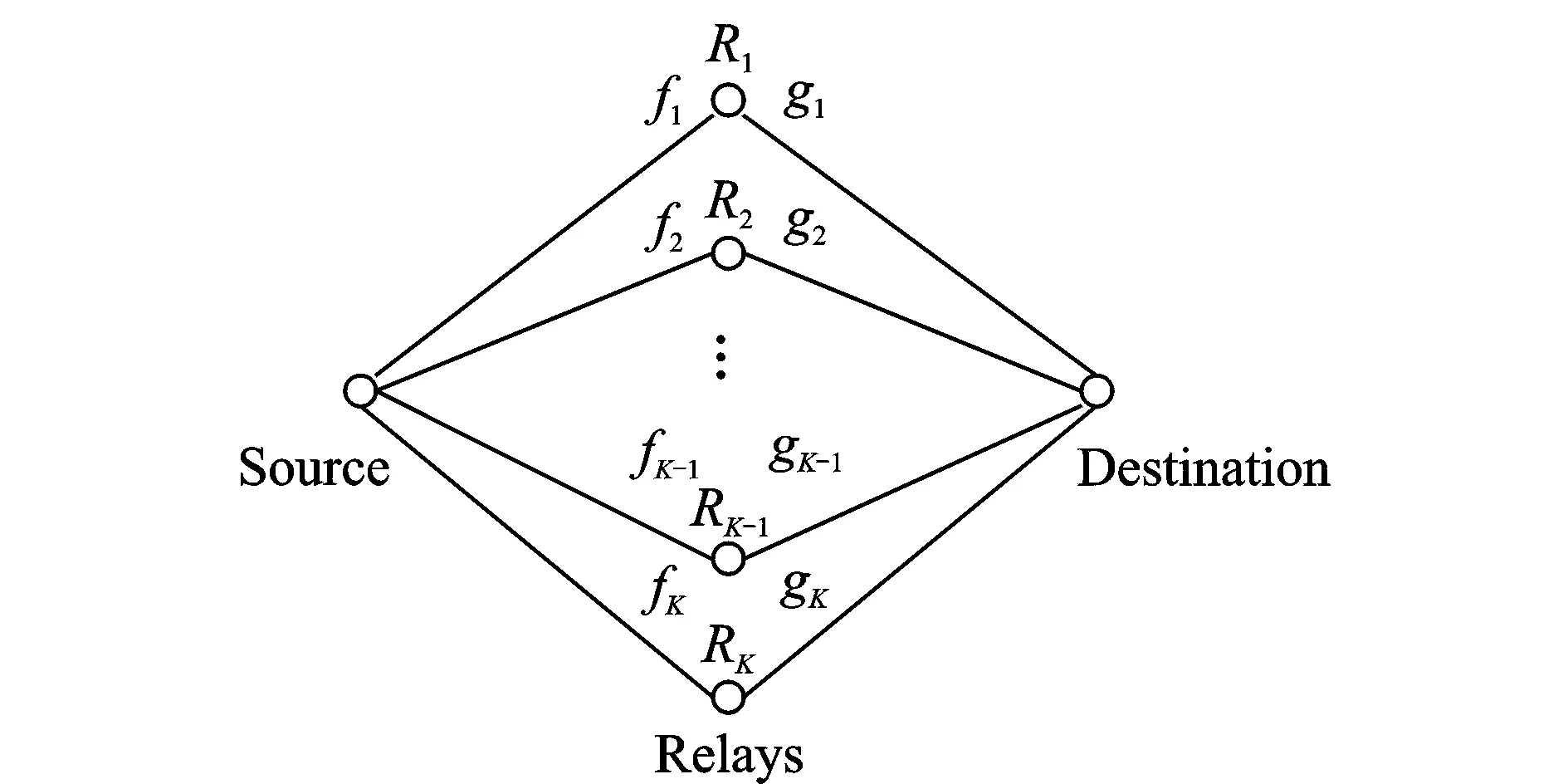
Fig.1 Cooperative wireless network model

(1)

whereri=(ri,1ri,2…ri,N) is the received symbol vector, andni=(ni,1ni,2…ni,N) is the complex additive white Gaussian noise (AWGN) atRiwith zero mean and identity covariance matrix. We assume the symbol vector from the source cannot be directly received by the destination. The same assumption has been made in many previous publications such as Refs.[1, 5—7]. Consider amplify-and-forward transmission at the relays. In the second stage, relayRifirst compensates forθiand obtains

(2)

(3)

(4)

is the equivalent noise at the destination. Notice thatXis aK×Tmatrix, whereTis the block length ofX, and stands for the decoding delay (delay for short in the rest of this paper). SinceXcontainsNinformation-bearing symbolsx1,x2,…,xNand lasts forTtime slots, the rate ofXis defined asR=N/T. It is easy to see that the mean ofnis zero and the covariance matrix ofnis given by

(5)

The maximum likelihood (ML) estimate of the symbol vectorxis given by

(6)

whereCis the set containing all the possible symbol vectorx.

2 Distributed Orthogonal Space-Time Block Code with Channel Phase Information

Definition 1 ( Yi and Kim[7]) AK×Tcomplex matrixXon complex variablesx1,x2,…,xNis called a DOSTBC-CPI if the following conditions are satisfied:

2)Xsatisfies the following equality

(7)

ItisshowninRef.[7]thattheupper-boundontherateofDOSTBC-CPIisexactly1/2,andthisupper-boundisachievablebythewell-knownrate-1/2TJCcode.Twoexamplesofrate-1/2DOSTBC-CPIareasfollows[7]

(8)

and

(9)

The latter is a TJC code for four antennas[8]. However, as shown in Refs.[9, 10], the delay of TJC code is not optimal. In the rest of this paper, we will propose an algorithm to construct maximal rate DOSTBC-CPI with lower delay.

3 Construction of Maximal Rate DOSTBC- CPI with Lower Delay

Refs.[9, 10] independently proposed the rate-1/2, zero-entry-free and minimal delay CODs. However, the COD in Ref.[9] depends on a complicated iterative algorithm, while the COD in Ref.[10] is not suitable to be used as DOSTBC-CPI since it is easy to verify thatΓin this case is not diagonal, which makes the decoding much harder.

Therefore, we propose an algorithm to construct a class of rate 1/2 zero-entry-free and low delay CODs so that when the COD is used as a DOSTBC-CPI and the noise covariance matrixΓis a scaled identity matrix. Due to space limitations, the detailed definition of balanced complex orthogonal design is illustrated in Definition 3.1 in Ref.[10]. The definition of column companion matrix is obtained by simply changing the ″row″ in Definition 4.1 in Ref.[10] into ″column″, and the definition of zero-masking column companion matrix is obtained by changing the ″row″ and ″column″ in Definition 4.2 in Ref.[10] into ″column″ and ″row″, respectively. The proofs of the following lemmas, theorem and corollary are omitted for the same reason.

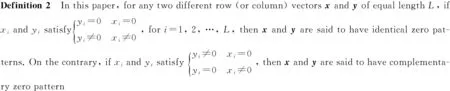
Lemma 1 Every columnlof a (2k, 2n,k) BCODPhas precisely one other partner columnl′ inPso that

(1)landl′ have complementary zero patterns;

(2)landl′ include the same variables;

(3) if any variableχappears inl, then it must appear asχ*inl′, and vice versa.

Such columnslandl′ are called zero-masking partners.

Lemma 2 Any (2k, 2n,k) BCODPhas a (2k, 2n,k) zero-masking column companion matrixQso that

(1) theith column ofQis the zero-masking partner of the ith column ofP;

(2) theith column ofQhas the same variables as theith column ofP;

(3) if any variableχappears in theith column ofP, then it must appear asχ*in theith column ofQ, and vice versa, for all 1≤i≤2n.

The idea of the following Theorem is similar to Theorem 5.2 of Ref.[10].

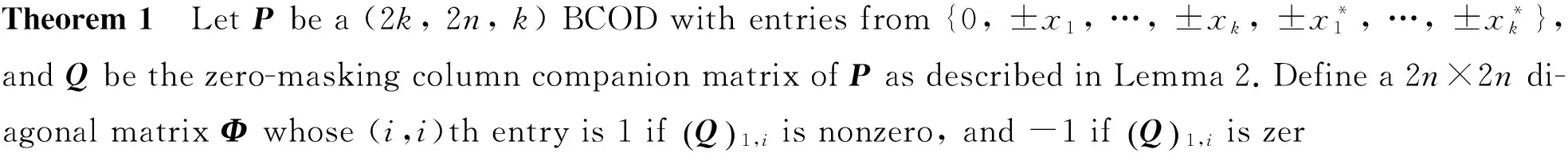
Like Theorem 5.2 of Ref.[10], Theorem 1 also provides an algorithm for constructing a class of rate-1/2, zero-entry-free CODs for any number of columns when followed by column deletion as necessary. Similar to the rate 1/2, zero-entry-free and minimal delay COD constructed in section V of Ref.[10], our design is also derived from BCODs that are generated via the modified-Liang algorithm in Ref.[10]. Hence following the method used in Ref.[10], it is not difficult to prove that the new rate-1/2 zero-entry-free CODs also have only half the delay of the TJC code and can achieve the lower bound on delay for most numbers of columns.

In addition，the property of not containing any zero entry not only avoids the need to switch on and off the antennas frequently, but also leads to low peak-to-average power ratio (PAPR)[10,12].

By transposing the rate-1/2 zero-entry-free CODs given above, we obtain a class of maximal rate DOSTBC-CPIs for cooperative wireless networks, which can achieve the lower bound on delay for most numbers of relays.

Corollary 1 When the rate-1/2 zero-entry-free COD constructed in Theorem 1 is used as a DOSTBC-CPI, the noise covariance matrixΓis a scaled identity matrix.

Example Consider the BCOD for six antennas in Ref.[10] that is generated via the modified Liang algorithm

(10)

Its zero masking column companion matrix is

(11)

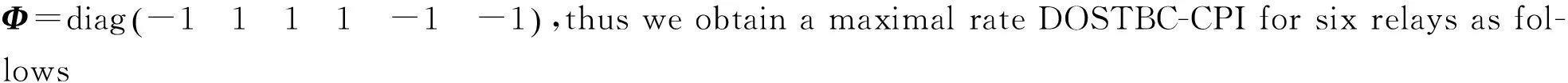
It is easy to verify that the noise covariance matrixΓis

Γ=E(nHn)=

(12)

The rate is 1/2 and the delay isT=8, which is the lower bound on delay for six relays ( for the lower bound on decoding delay of rate-1/2 CODs, see Refs.[9, 10] ).

For comparison, we list the TJC code for six relays as follows

(13)

The delay isT=16，which is twice that of the new code given above.

The DOSTBCs-CPI proposed in this paper have many desirable properties:

(1) They can achieve full diversity order and are single-symbol decodable since they are also CODs.

(2) They also achieve the rate 1/2, which is the upper-bound on the rate of DOSTBC-CPI.

(3) They have only half the delay of the TJC code, and can achieve the lower bound on delay for most numbers of relays like the rate 1/2 CODs in Refs.[9, 10].

(4) They have low PAPR since they do not contain any zero entry.

(5) They are obtained through a simple algebraic approach avoiding iterative algorithms.

4 Simulation Results

We consider a cooperative wireless network scenario in which one source node communicates with one destination node through the help ofKrelay nodes. The fading coefficients between the source and the relaysfi, and between the relays and the destinationgi, are modeled as independent complex Gaussian random variables with zero-mean and unit-variance.fiandgiare assumed to keep constant for the entire transmission of one code block. The noises at the relays and the destination are modeled as independent zero-mean unit-variance Gaussian additive noise. We compare the performance of the proposed code and the TJC code in terms of SER versusPs, the power used by the source node per channel use. The optimum power allocation proposed in Ref.[1] is adopted, i.e.Pr=Ps/K. Since the proposed code and the TJC code both have rate 1/2, they employ the same signal sets to achieve the same bandwidth efficiency. Hence QPSK, 8PSK and 16QAM are employed for both codes to achieve bandwidth efficiency of 1 b/(s·Hz), 3/2 b/(s·Hz) and 2 b/(s·Hz), respectively. The symbol vectors are decoded symbol by symbol via ML estimation algorithm given in Eq.(6). The SER performance is obtained by source sending 107symbols at a time.

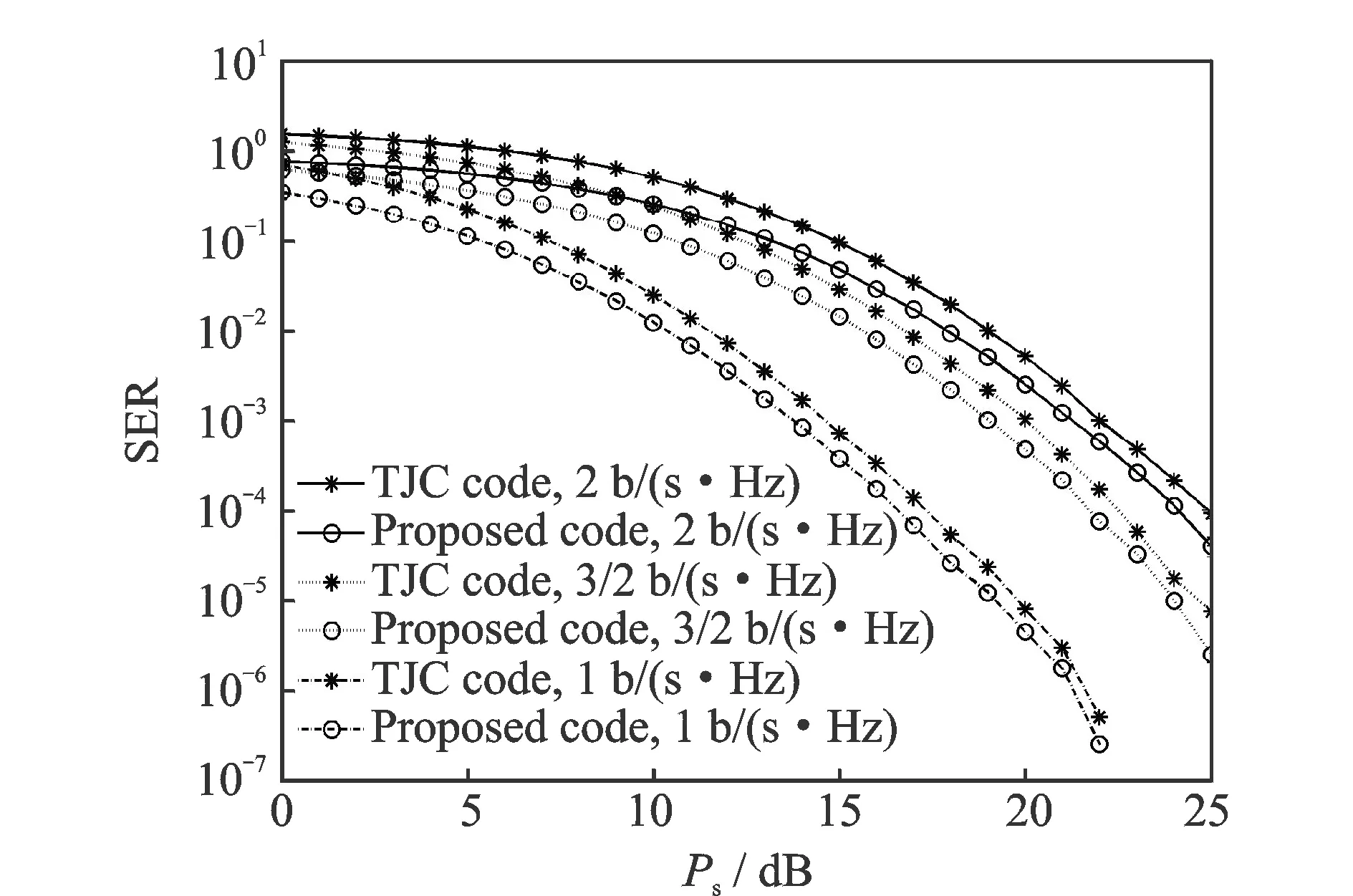
Fig.2 SER performance comparison of the proposed code and TJC code for K=6

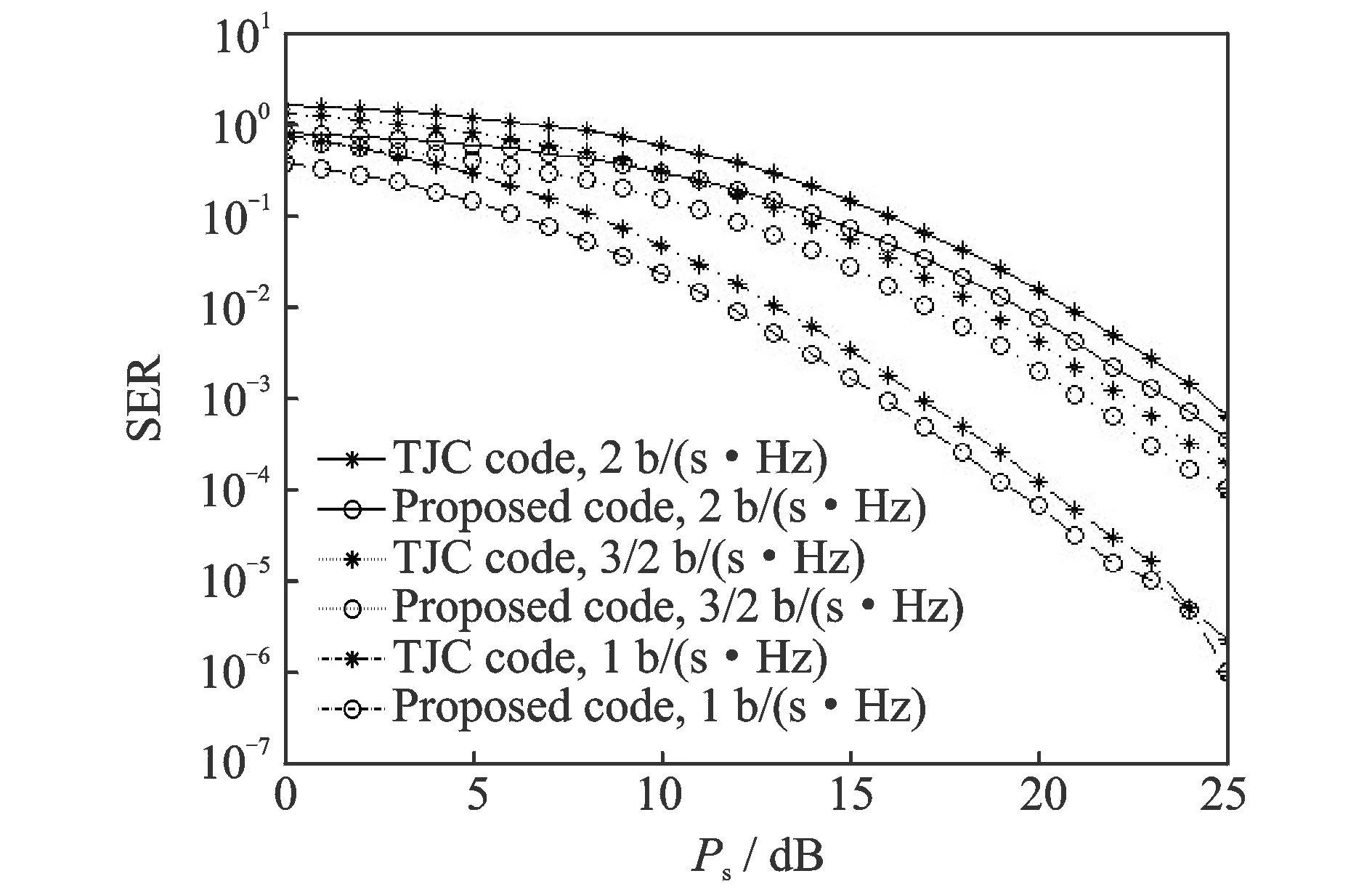
Fig.3 SER performance comparison of the proposed code and the TJC code for K=4

Fig.2 compares the SER performance of the proposed code and the TJC code for six relays given in Eq.(13). Fig.3 shows the SER performance comparison of the proposed code and the TJC code for four relays. As we have expected, the proposed code provides full diversity, for the same bandwidth efficiency, the SER curve of the proposed code moves parallel to that of the TJC code. Also as expected, the proposed code achieves the same diversity order for different modulation schemes, since at large values ofPs, the SER curves of the proposed code for different modulation schemes are parallel to each other. The reason for these is that the diversity order that a DOSTBC can provide in high SNR region is determined by the number of relays. It is also observed that for same bandwidth efficiency, the proposed code outperforms the TJC code by about 1—2 dB. Therefore, the proposed code outperforms the TJC code in SER performance as well as in decoding delay.

5 Conclusions

We propose an algorithm to construct a class of maximal rate DOSTBC-CPIs with half the decoding delay of the TJC code. The proposed method not only hold all the desirable properties of the TJC code such as full diversity order, maximal rate, single-symbol decodable, low PAPR, noise covariance matrix being a scaled identity matrix and obtained through a simple algebraic approach, but also outperform the latter in SER performance as well as in decoding delay.

Acknowledgements

This work was supported in part by the National Natural Science Foundation of China (Nos. 61271230, 61472190), and the National Mobile Communications Research Laboratory, Southeast University (No. 2013D02).

[1] JING Y, HASSIBI B. Distributed space-time coding in wireless relay networks [J]. IEEE Transactions on Wireless Communication, 2006, 5(12): 3524-3536.

[2] JING Y, JAFARKHANI H. Using orthogonal and quasi-orthogonal designs in wireless relay networks[J].IEEE Transactions on Information Theory, 2007, 53 (11): 4106-4118.

[3] HAN J, CHOI J, SEO J. Cooperative space-time block coded full-duplex relaying over frequency-selective channel [J]. IET Communications, 2015, 9 (7): 960-968.

[4] ABOURJEILY C. Distributed space-time codes for full-duplex IR-UWB amplify-and-forward cooperation [J]. IEEE Transactions on Wireless Communication, 2015, 14 (4): 2144-2155.

[5] YI Z, KIM I M. Single-symbol ML decodable distributed STBCs for cooperative networks [J]. IEEE Transactions on Information Theory, 2007, 53 (8): 2977-2985.

[6] SREEDHAR D, CHOCKALINGAM A, RAJAN B S. Single-symbol ML decodable distributed STBCs for partially-coherent cooperative networks [J]. IEEE Transactions on Wireless Communication, 2009, 8 (5): 2672-2681.

[7] YI Z, KIM I M. Symbol rate upper-bound on distributed STBC with channel phase information [J]. IEEE Transactions on Wireless Communication, 2011, 10 (3): 745-750.

[8] TAROKH V, JAFARKHANI H, CALDERBANK A R. Space-time block codes from orthogonal designs [J]. IEEE Transactions on Information Theory, 1999, 45 (7): 1456-1467.

[9] DAS S, RAJAN B S. Low-delay, high-rate nonsquare complex orthogonal designs [J]. IEEE Transactions on Information Theory, 2012, 58 (5): 2633-2647.

[10]ADAMS S S, DAVIS J, KARST N, et al. Novel classes of minimal delay and low PAPR rate 1/2 complex orthogonal designs [J]. IEEE Transactions on Information Theory, 2011, 57(4): 2254-2262.

[11]HARSHAN J, RAJAN B S. Distributed space-time block codes for two-hop wireless relay networks [J]. Journal of Communications, 2010, 5(4): 282-296.

[12]YUEN C, GUAN Y L, TJHUNG T T. Power-bananced orthogonal space-time block code [J]. IEEE Transactions on Vehicular Technology, 2008, 57 (5): 3304-3309.

Mr. Chen Junsheng is currently a lecturer in College of Information Engineering, Yangzhou University. His research interests include multiuser detection, cooperative communications and distributive space-time coding.

Prof. Zhang Xiaofei is currently a full professor and Ph.D. supervisor in College of Electronic and Information Engineering, Nanjing University of Aeronautics and Astronautics. His research interests mainly include communication signal processing, array signal processing and MIMO radar.

Prof. Shu Feng is currently a full professor and Ph.D. supervisor in School of Electronic and Optical Engineering, Nanjing University of Science and Technology. His research interests include wireless networking, and radar signal processing.

Prof. Wang Jianxin is currently vice dean and also a full professor and Ph.D. supervisor in School of Electronic and Optical Engineering, Nanjing University of Science and Technology. His main research areas are communications signal processing and software radio.

(Executive Editor： Zhang Bei)

TN929.5 Document code:A Article ID:1005-1120(2016)06-0726-07

*Corresponding author, E-mail address: jschen@yzu.edu.cn. How to cite this article: Chen Junsheng, Zhang Xiaofei, Shu Feng, et al. Construction of low delay maximal rate single-symbol decodable distributed STBC with channel phase information[J]. Trans. Nanjing Univ. Aero. Astro., 2016,33(6):726-732. http://dx.doi.org/10.16356/j.1005-1120.2016.06.726