考虑土-结构相互作用的黏弹性减震结构的简化设计方法①

赵学斐， 王曙光， 杜东升， 刘伟庆

(南京工业大学土木工程学院， 江苏 南京 210009)

考虑土-结构相互作用的黏弹性减震结构的简化设计方法①

赵学斐， 王曙光， 杜东升， 刘伟庆

(南京工业大学土木工程学院， 江苏 南京 210009)

首先在频域中建立了考虑土-结构相互作用(SSI)的黏弹性阻尼单自由度消能减震结构体系的动力平衡方程,通过模态应变能法及结构体系的传递函数,推导出了结构体系等效周期及等效阻尼比的计算方法，并参数化分析了SSI效应对消能减震结构的影响。结果表明结构的高宽比及初始附加阻尼比对阻尼器的减震效率影响较大。通过等效方法将质量刚度分布比较均匀的多自由度减震框架体系简化为单质点体系进行抗震分析。算例表明该方法具有一定的精度，对考虑SSI效应的消能减震结构体系的抗震评估具有一定的工程应用价值。

土-结构相互作用； 减震结构; 黏弹性阻尼器； 等效方法

引 言

消能减震结构通过在结构中设置消能装置来吸收地震能量，从而减轻主体结构的地震反应或其他动力反应，提高结构的安全性与经济性等要求。近几十年来，消能减震技术迅速发展，得到越来越多的关注和工程应用[1-3]。由于土-结构相互作用问题分析的复杂性，在进行结构的抗震设计时，结构工程师常采用刚性地基假定，此种假定在地基刚度比较大时是可行的，而对于软土地基，该假定并不一定总是安全。消能减震装置在增加结构阻尼的同时也增加了结构的刚度，使结构的动力特性发生一定程度的变化。土-结构刚度比作为SSI问题中的敏感性参数之一将很大程度上影响结构的地震反应。因此，对建立在较软弱地基上的消能减震结构，忽略SSI效应将对分析结果将带来一定的误差，所以有必要对考虑SSI效应的消能减震结构的地震反应进行探讨和研究。

目前，关于SSI效应对消能减震结构影响的研究相对较少。宋和平[4]等结合实际工程，对地震作用下消能减震结构体系进行了分析，结果表明，在考虑SSI效应后，减震效果明显变差。张兆超[5]通过数值算例分析，认为SSI作用降低了消能装置的有效性，基于刚性地基假定进行高层结构的减震控制和抗震性能评价并不一定偏于安全。但以往的研究一般根据工程实例计算结果得出结论，缺乏系统性和推广性。

本文在以往学者研究成果的基础上提出了考虑SSI效应的单自由度黏弹性阻尼减震结构等效周期和等效阻尼比的计算方法，并采用等效方法将质量刚度分布较均匀的多自由度减震框架体系简化为单质点体系进行抗震分析，为考虑SSI效应的减震框架结构的地震反应评估提供了一种简单可行的分析方法。

1 考虑SSI效应的单自由度黏弹性阻尼减震体系的动力平衡方程

本文首先考虑了具有埋置基础的单自由度减震结构体系，如图1所示。沿基础上表面可将结构体系分为上部结构和下部基础两部分，结构与基础上表面之间有剪力和弯矩传递。上部结构的运动方程可写成如下形式：

(1)

(2)

(3)

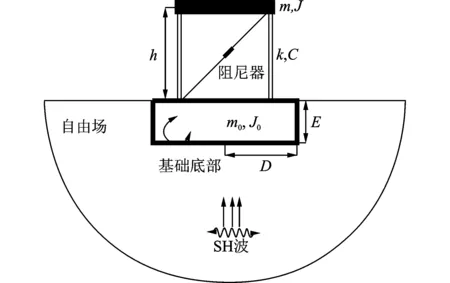
图1 考虑SSI效应的单自由度减震体系Fig.1 The SDOF energy dissipated structure considering SSI

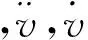
通过傅里叶变换，运动方程在频域中的表达式如下：

(4)

(5)

(6)

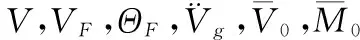
黏弹性阻尼器本构采用Makris[6]提出的五参数分数导数模型，其具体表达式如下

(7)

其中

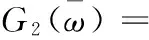
表达式中具体参数通过实验数据拟合得到，其中：k=0,c0=15kN/m ,b=0.3 s0.6,α=1，β=0.6。实部刚度与虚部刚度及阻尼系数随频率的变化如图2所示。

考虑剪切面积与剪切厚度的影响，阻尼器复刚度表达式如下所示

(8)

式中As为黏弹性阻尼器剪切面积，d为剪切厚度。

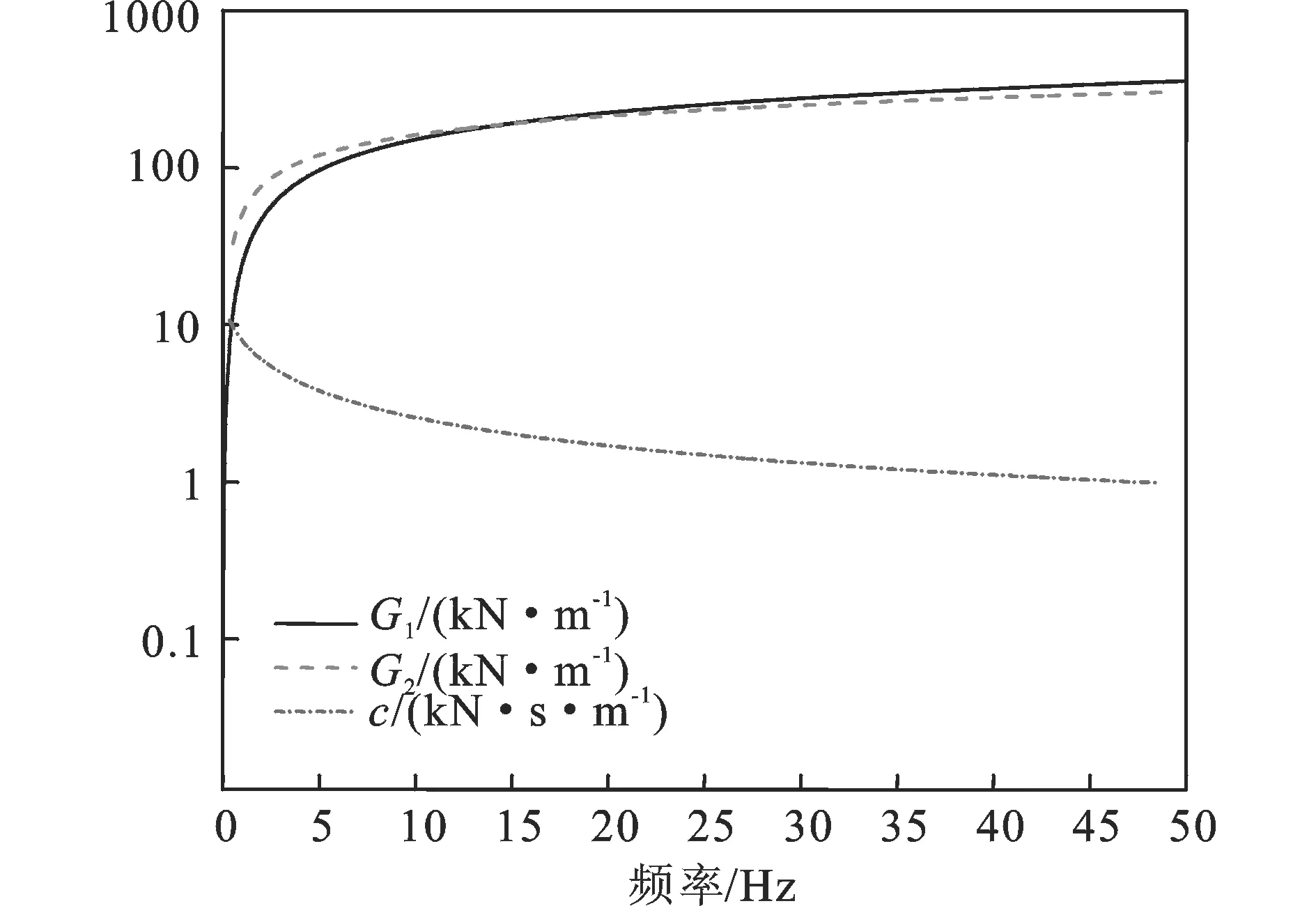
图2 黏弹性阻尼复刚度及阻尼系数Fig.2 The complex stiffness and damping coefficient of VED

下部基础与土体相互作用的平衡方程如下所示：

(9)

式中Ghh,Ghr,Grh,Grr分别表示基础的水平阻抗，水平-回转耦合阻抗，回转-水平耦合阻抗，回转阻抗。其通常具有如下统一的表达式

G(ia0)=GR(a0)+iGI(a0)

(10)

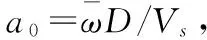
基础的存在会对地震波的传播产生一定程度的影响，从而造成输入结构的地震动与自由场地震动是不相同的，这种现象称之为土-结运动相互作用。基础的存在一般会对自由场水平地震动不同频段的傅里叶幅值产生一定的削弱作用，与此同时产生回转地震动。本文使用原田提出的基础输入运动的近似公式[7]来考虑土结动力相互作用问题。水平、回转分量如下所示:

水平分量：

(11)

回转分量：

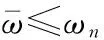
(12)

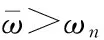
(13)

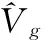
综上，同时考虑土-结运动相互作用与惯性相互作用的单自由度黏弹性阻尼减震结构体系的动力平衡方程如下表示：

(14)

表达式中具体参数如下所示

IT=mh2+J+J0

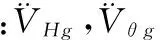
式(14)可变换为如下形式

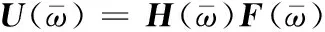
(15)

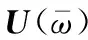
2 结构体系的等效周期与等效阻尼比

直接求解考虑SSI效应的消能减震结构体系的地震动反应比较繁琐，若能将原结构体系简化为在固定基础上的具有等效周期及阻尼比的单质点体系(即将图1所示结构体系等效为图3所示结构体系)，则问题不仅将得到大大简化，结构体系还可在时域中进行等效分析。本节在以往学者对减震结构及土结相互作用研究成果的基础上，提出了能够考虑SSI效应的消能减震结构体系等效周期及阻尼比的计算方法，并对等效结果的精度进行了验证。

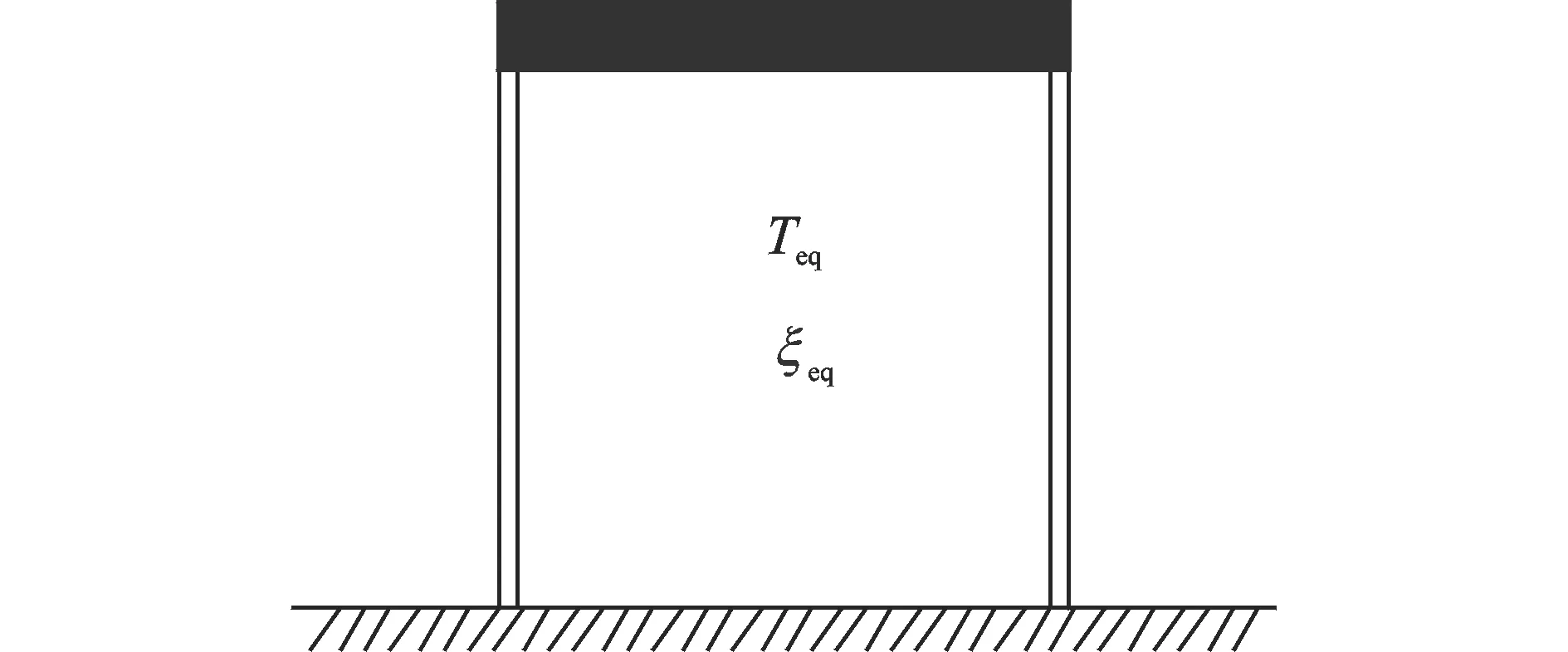
图3 固定基础等效单自由度体系Fig.3 The equivalent SDOF system on fixed base

首先考虑固定基础上单质点黏弹性阻尼减震体系，其动力方程在频域中的表达式如下所示

(16)

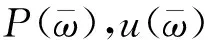
(17)

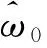
(18)

结合式(14)与(18)，定义如式(17)所示的复频传递函数

(19)

式中V为上部结构集中质量质心处相对与基础表面的位移的傅里叶变换，Vg为自由场地位移的傅里叶变换。

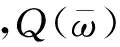
(20)

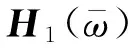
体系的等效阻尼比及等效周期可采用共振传递函数[9]得到，其表达式如下所示：

(21)

(22)

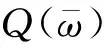
为验证该等效计算方法的精度，对以上过程通过Matlab编程进行数值检验。模型基本参数为：基础采用埋置圆形基础，半径D=10 m，埋深E=5 m，其阻抗函数根据Kausel[10]提出的简化方法计算求得；上部结构周期T=0.7 s，阻尼比ξ=0.05；土体密度ρ=2000 kg/m3，泊松比ν=0.4, 剪切波速Vs=100 m/s；结构-土体质量比δ=15 %(其中δ=m/(ρπD2h)); 阻尼器对固定基础结构提供的初始附加阻尼比分别取0，5%，10%，15%(可通过模态应变能方法求得[8])。

图4～7给出了等效方法与SSI减震体系结构顶部位移响应功率谱的对比情况(地震波采用El-Centro波南北向输入，加速度峰值0.3g)。图8及9给出了初始附加阻尼比为分别为5%，15%的等效方法与SSI减震体系计算所得位移时程对比情况

可以看出无论在频域还是时域中，等效方法与原减震体系的计算结果均吻合得很好。

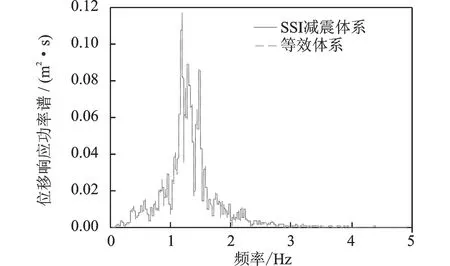
图4 位移响应功率谱对比(无阻尼器)Fig.4 Comparison of displacement PSD(No damper)

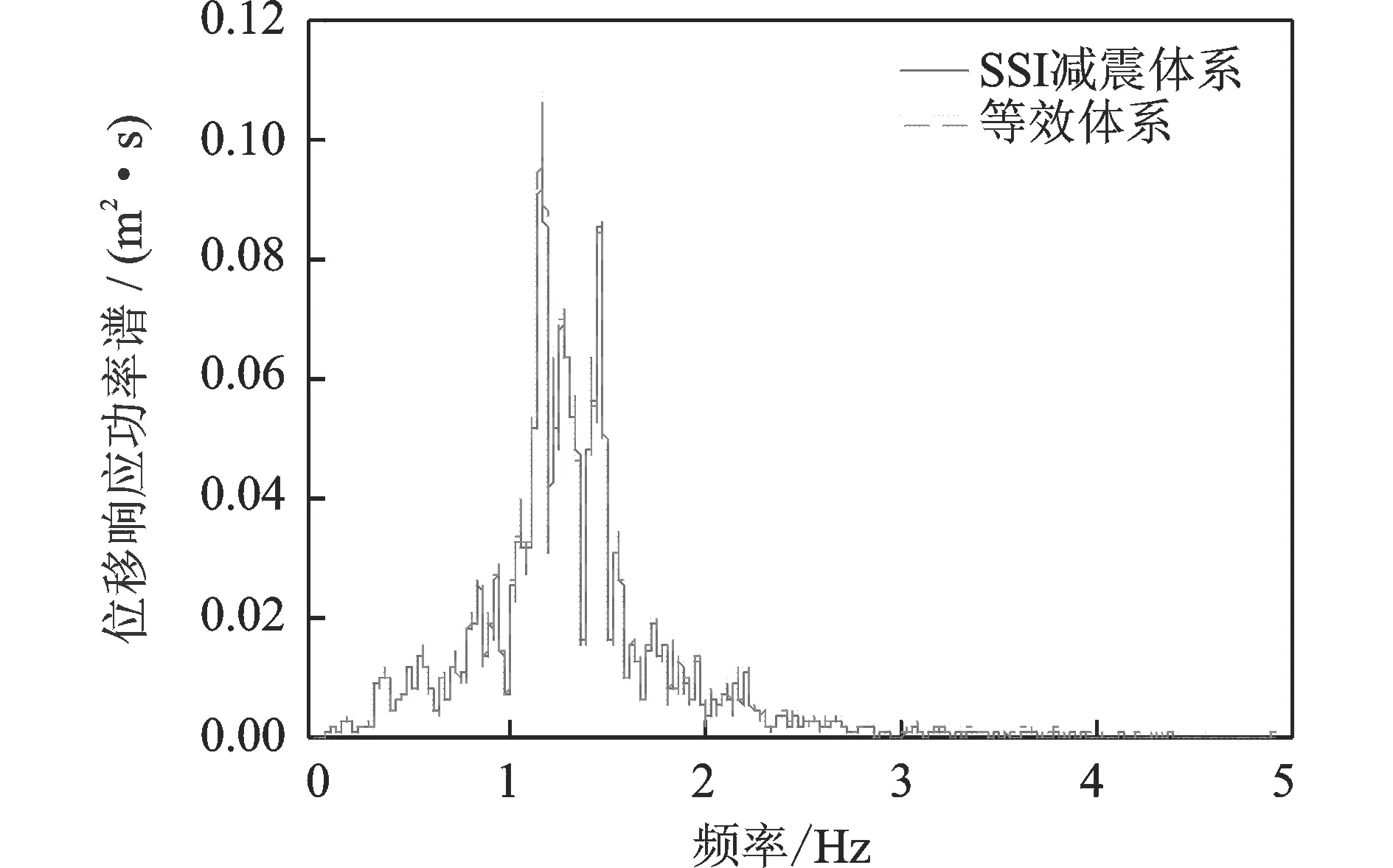
图5 位移响应功率谱对比(5%附加阻尼比)Fig.5 Comparison of displacement PSD(5% additional damping)

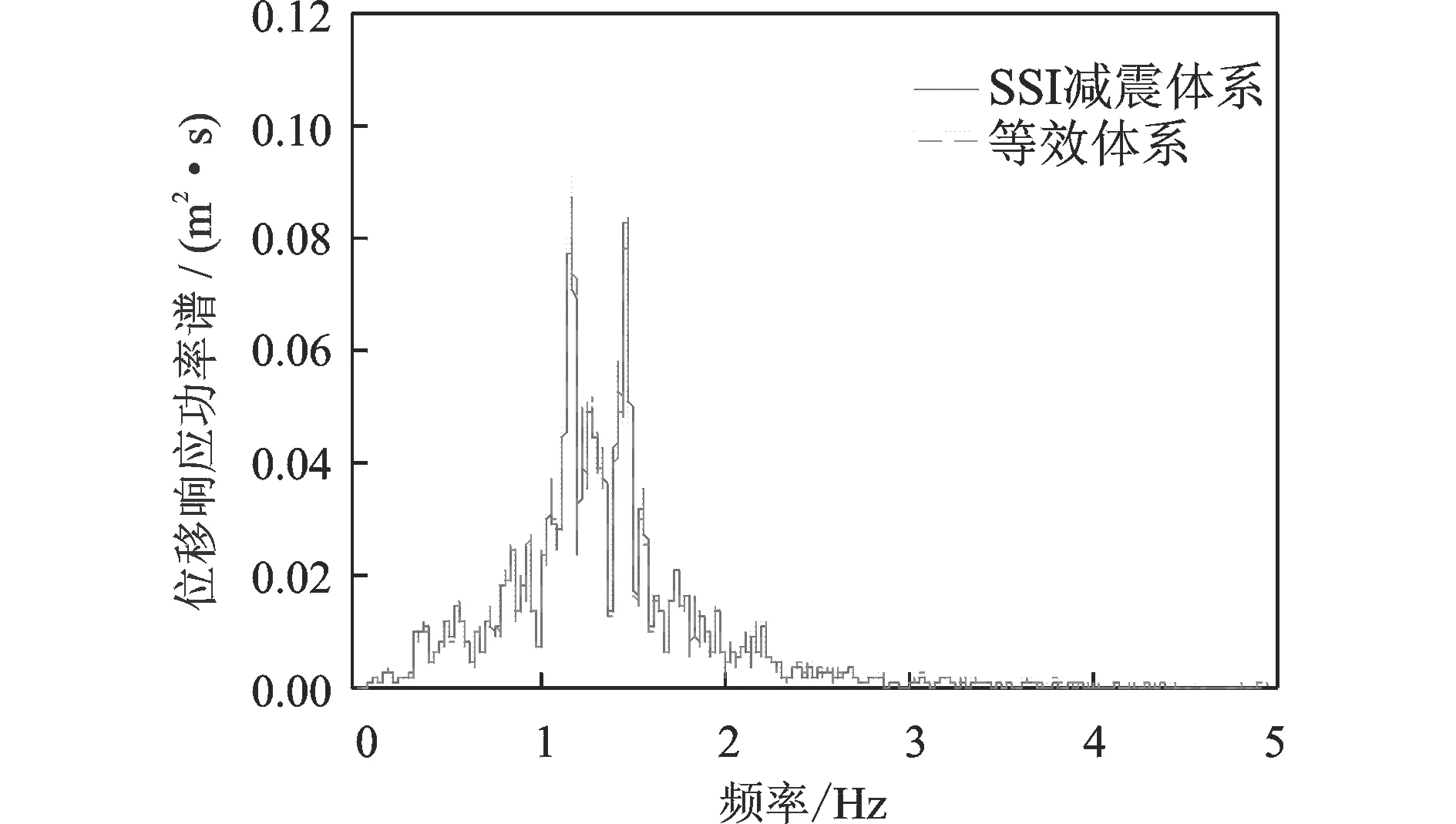
图6 位移响应功率谱对比(10%附加阻尼比) Fig.6 Comparison of displacement PSD(10% additional damping)

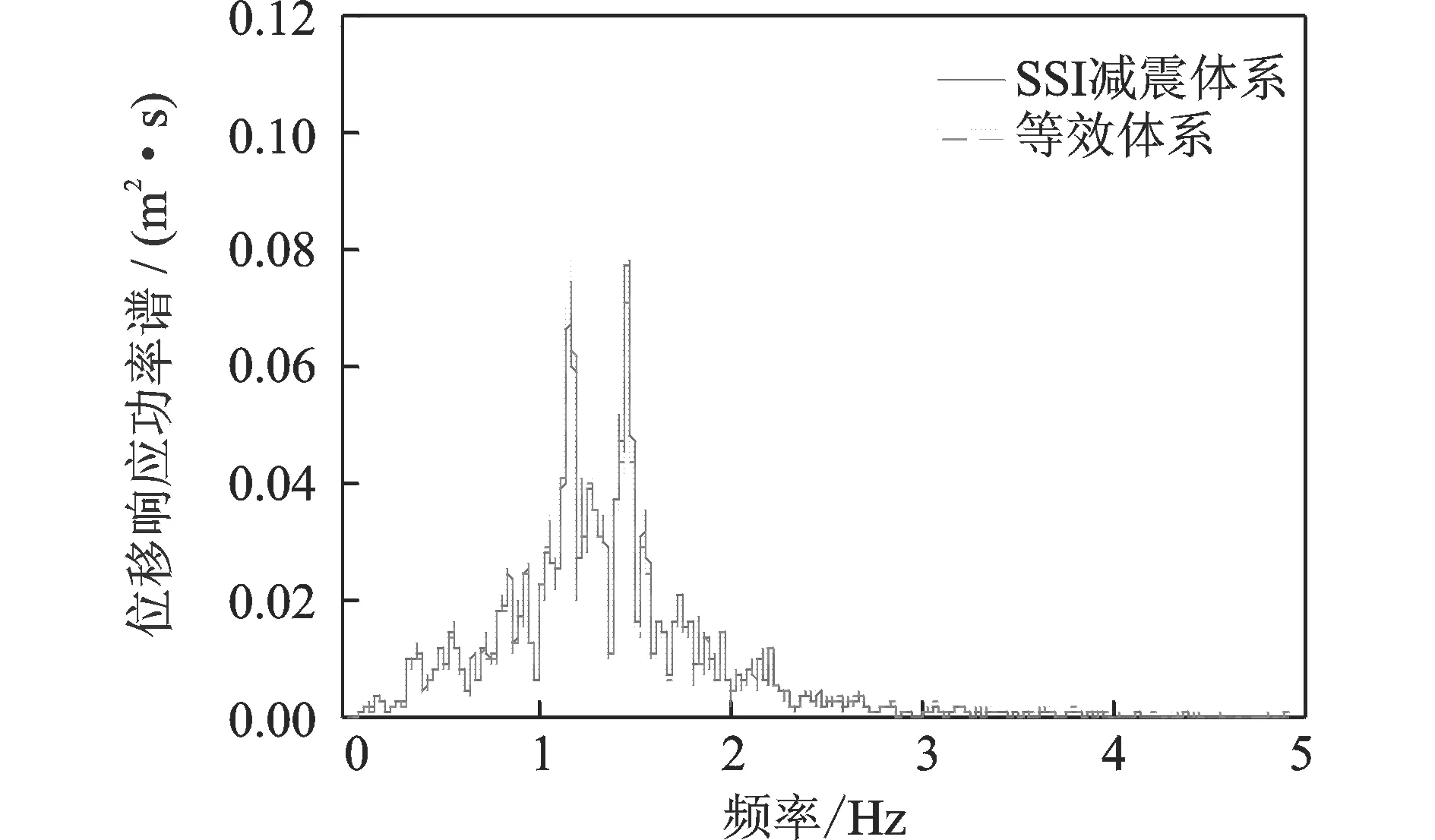
图7 位移响应功率谱对比(15%附加阻尼比)Fig.7 Comparison of displacement PSD(15% additional damping)

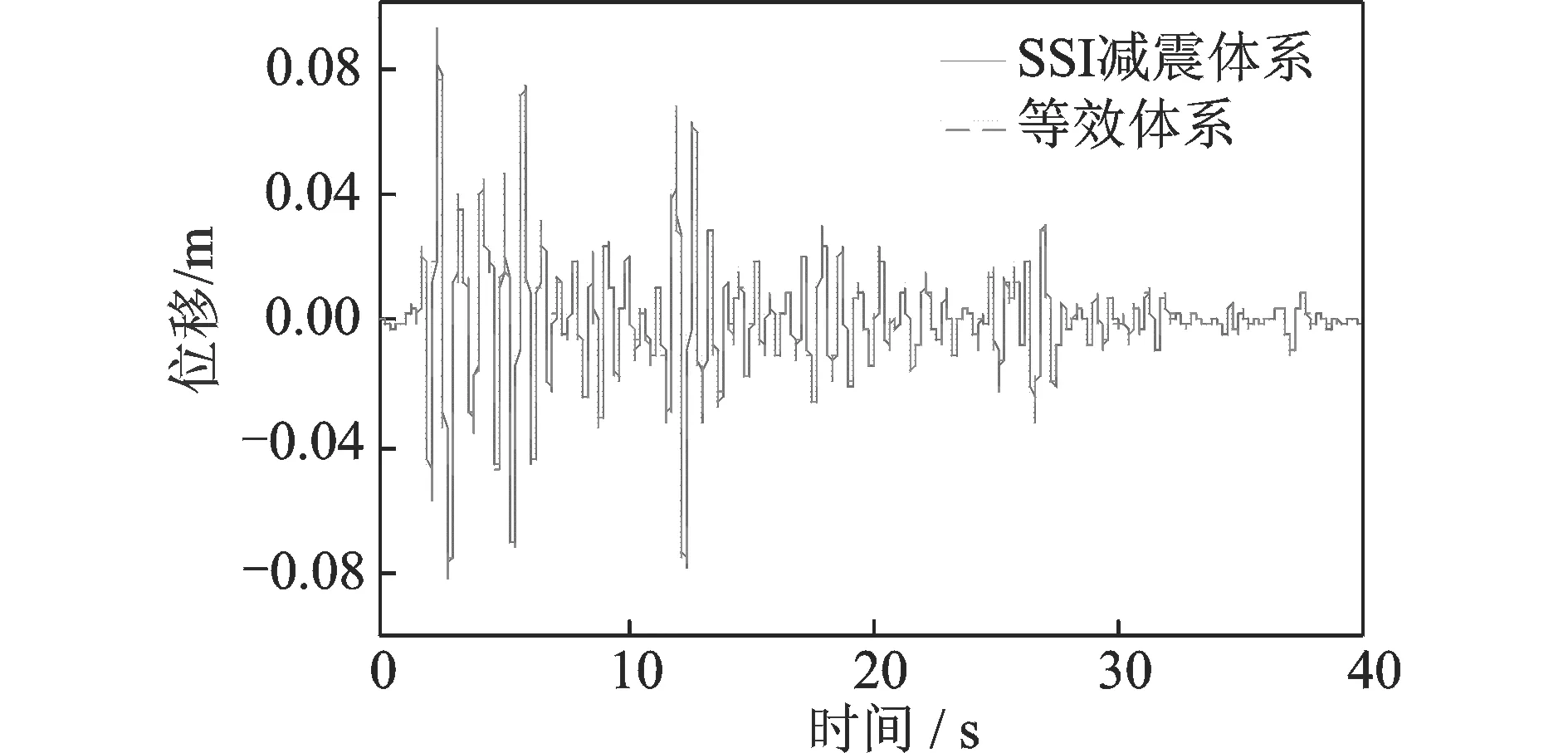
图8 5%附加阻尼比等效体系与SSI减震体系位移时程对比Fig.8 The comparison of displacement time history between equivalent method and SSI system(5% additional damping)

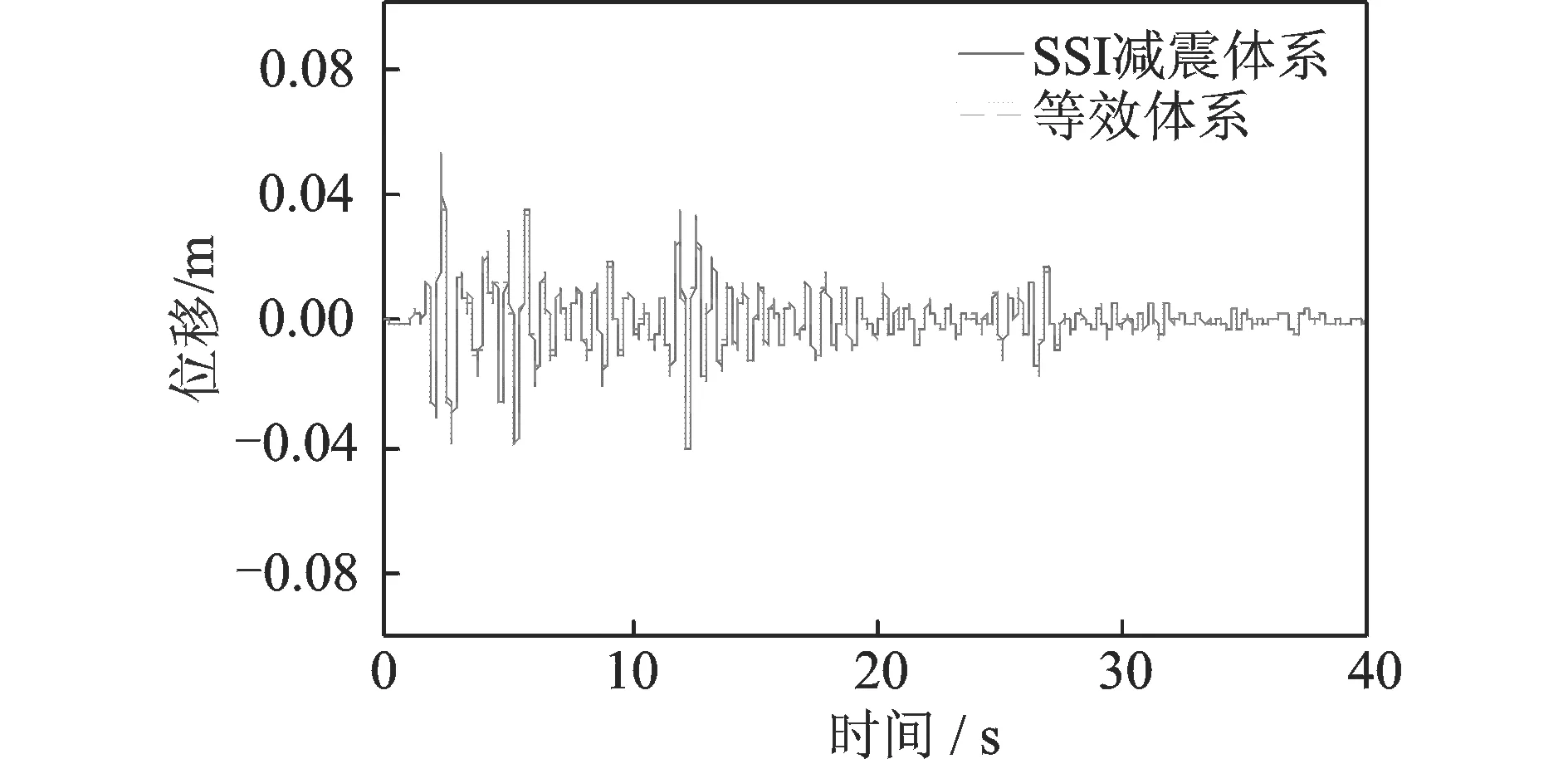
图9 15%附加阻尼比等效方法与SSI减震体系位移时程对比Fig.9 The comparison of displacement time history between equivalent method and SSI system(15% additional damping)

3 SSI效应对黏弹性阻尼减震结构影响的参数化分析

本节通过第2节提出的简化方法参数化研究了结构高宽比h/D，基础埋深比E/D，阻尼器提供的附加阻尼比以及土体-结构体刚度比σ=VsT/h(其倒数形式为α=1/σ)四种参数对结构体系等效周期及等效阻尼比的影响。所有工况保持结构-土体质量比δ=15%不变，结构初始阻尼比ξs=0.05。为考虑动力相互作用对结构体系的影响，分别计算了只考虑惯性相互作用(基础输入地震波同自由场)与同时考虑惯性相互作用与运动相互作用结构体系的等效周期及等效阻尼比。

图10给出了基础半径D=10 m，不同参数下，结构体系等效周期延长率的变化情况。图中T为结构体系的等效周期，T0为未增设阻尼器的结构在固定基础上的周期。ξ0表征在固定基础情况下阻尼器所提供的附加阻尼比(例如：ξ0=5%表征阻尼器提供5%的附加阻尼比)。

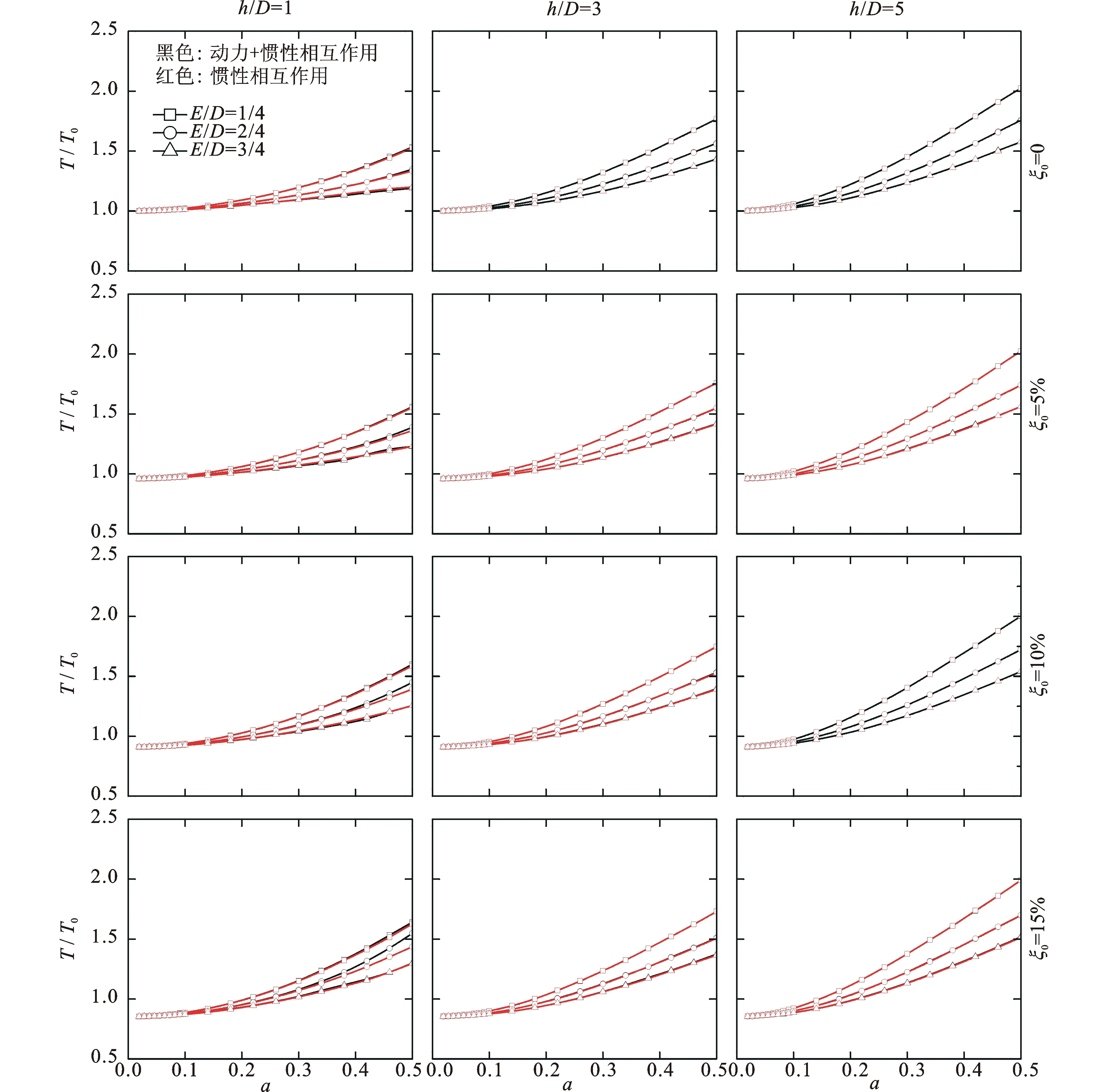
图10 不同参数对体系等效周期的影响Fig.10 The influence of different parameters on the equivalent period

等效周期在不同参数影响下的变化规律可归纳如下：(1)同时考虑土-结运动相互作用与惯性相互作用与只考虑土-结惯性相互作用情况下结构的等效周期基本一致，因此在计算结构体系的等效周期时可以忽略运动相互作用, 而只考虑惯性相互作用；(2)随着基础埋深的增加，结构体系的等效周期具有一定程度的下降，该趋势随着土体的变软而更加明显；(3)结构高宽比越大，等效周期越大。

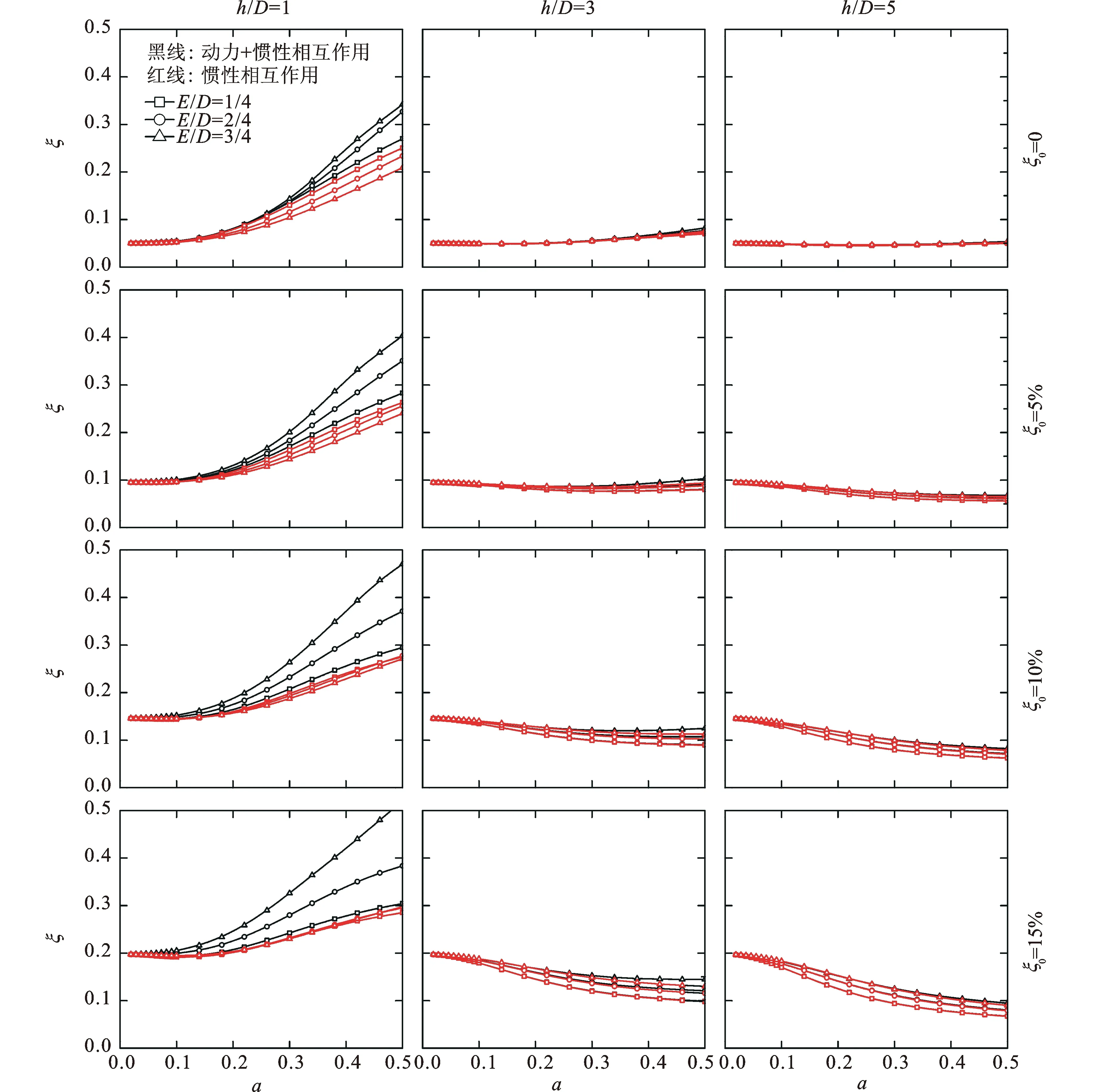
图11 不同参数对体系等效周期及等效阻尼比的影响Fig.11 The influence of different parameters on equivalent damping ratio

图11给出了基础半径D=10 m，不同参数下，结构体系等效阻尼比ξ的变化情况。

等效阻尼比在不同参数影响下的变化规律如下：(1)当结构高宽比较小(h/D=1)时，只考虑惯性相互作用与同时考虑惯性相互作用与运动相互作用所计算得出的等效阻尼比具有明显的差异，这种差异程度随着基础埋深的增加与附加阻尼比的增加而更加明显。而当结构高宽比变大时，运动相互作用的影响可逐渐忽略。(2)基础的埋深越大，结构体系的等效阻尼比越大。(3)当结构高宽比较小时(h/D=1)，结构体系的等效阻尼比随土体的变软而增加，而随着结构高宽比变大及初始附加阻尼比的提高，结构体系的等效阻尼比下降程度逐渐增加。说明对建在软土地基上的具有高附加阻尼比的高层减震结构，阻尼器的减震效率同固定基础的设计目标相比具有很大程度的下降。

4 考虑SSI效应的多质点黏弹性减震结构地震反应简化评估

质量及刚度分布较为均为的多自由度框架结构的地震反应通常可等效为单质点结构体系进行分析。其等效质量可写为如下的表达形式[11]

(23)

式中φj1为第一振型第j层分量，mj为第j层质量。

等效高度可写为如下表达形式

(24)

式中Hj为第j层质心处相对于基础上表面高度。

阻尼器布置按层刚度比例分配

(25)

式中Kj为第j层刚度值，p为比例系数。

单质点体系的周期与多质点体系一阶周期相同，则等效刚度可通过下式计算得出

(26)

单质点体系附加阻尼器存储刚度根据式(25)中的比例系数p得到，则考虑SSI效应的多质点消能减震结构体系等效为了单质点结构体系，从而可通过第2节提出的简化方法进行地震反应分析。

5 算例分析

为验证上述方法的可行性，本节建立了考虑SSI效应的四层减震框架结构的数值模型，基础采用埋置圆形基础，基础半径D=10 m，埋深E=5 m。土体剪切波速考虑三种情况，Vs=100 m/s，200 m/s, 300 m/s，分别定义为Case1,Case2,Case3,以研究不同土性对计算结果以及计算精度的影响。土体密度ρ=2000 kg/m3, 泊松比ν=0.4。表1给出了结构及阻尼器的相关参数。

根据式(23)及(24)的等效原则，将原结构等效为单自由度体系，其等效质量Meq=1.54×106kg,等效高度Heq=11.8 m, 结构第一振型周期为T=0.718 s。按照等刚度比例原则，等效单自由度体系阻尼器的形状系数As/d=920 mm。

表1 四层结构参数

Tab.1 The parameters of four story structure

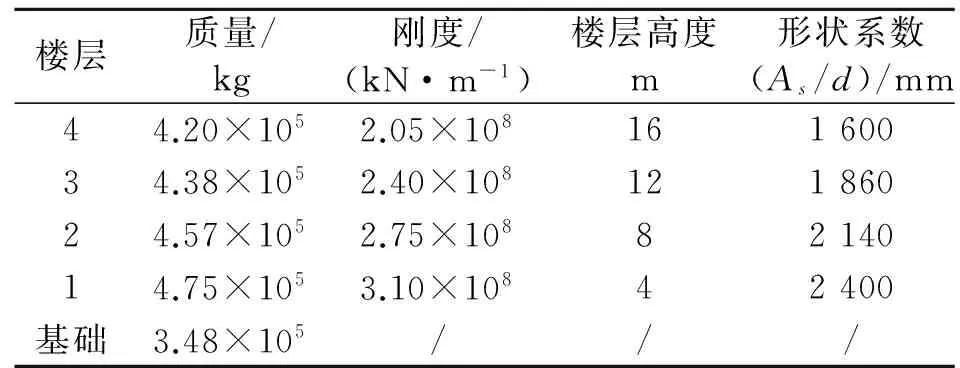
楼层质量/kg刚度/(kN·m-1)楼层高度m形状系数(As/d)/mm44.20×1052.05×10816160034.38×1052.40×10812186024.57×1052.75×1088214014.75×1053.10×10842400基础3.48×105///

等效单自由度体系参数确定后，通过第2节提出的等效周期及等效阻尼比计算公式得到结构体系在不同土体情况下的等效周期与等效阻尼比。对Case1, 等效周期Teq=0.728 s，等效阻尼比ξeq=0.161；对Case2，Teq=0.683 s，ξeq=0.158；对Case 3,Teq=0.671 s，ξeq=0.155。

地震输入采用El-Centro波和Kobe波，加速度峰值均调整为0.3g。采用Matlab分别计算了原四层减震结构的地震反应和等效单自由度结构的地震反应。

图12～15给出了等效体系与SSI减震体系在El-Centro波输入下，顶部加速度及位移地震反应时程的对比情况。图16～19给出了等效体系与SSI减震体系在Kobe波输入下，顶部加速度及位移地震反应时程的对比情况。由于篇幅有限，并未列出所有工况的时程对比。

表2给出了所有工况下等效体系与SSI减震体系地震反应峰值的对比情况及其误差分析。

通过图表可以看出：采用本文提出的简化设计方法对于质量刚度分布比较均匀的以第一振型为主的框架结构，其计算误差比较小，具有较高的精度。

表2 地震反应峰值对比和误差分析

Tab.2 Comparison of the peak seismic responses and error analysis

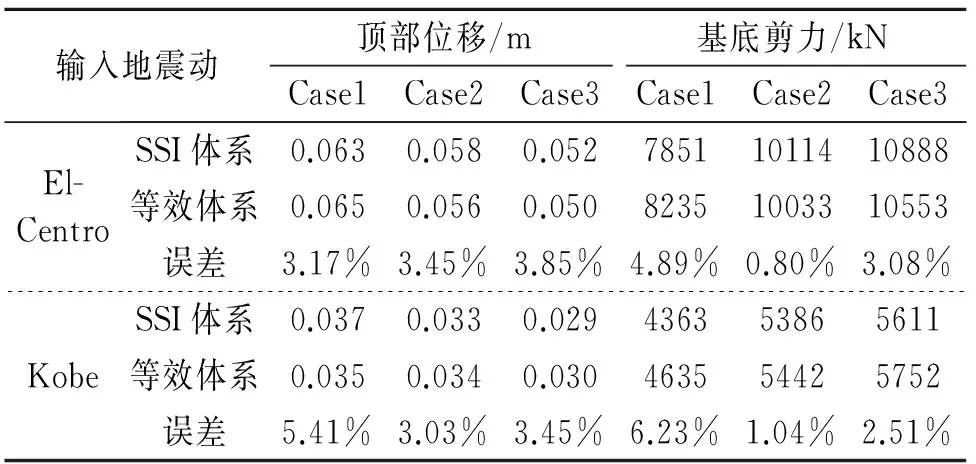
输入地震动顶部位移/m基底剪力/kNCase1Case2Case3Case1Case2Case3El-CentroSSI体系0.0630.0580.05278511011410888等效体系0.0650.0560.05082351003310553误差3.17%3.45%3.85%4.89%0.80%3.08%KobeSSI体系0.0370.0330.029436353865611等效体系0.0350.0340.030463554425752误差5.41%3.03%3.45%6.23%1.04%2.51%

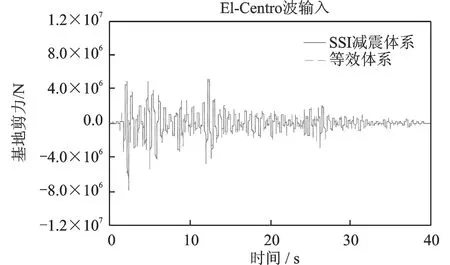
图12 等效体系与原结构体系基底剪力对比(Vs=100 m/s)Fig.12 Comparison of base shear force between equivalent system and the original SSI system(Vs=100 m/s)

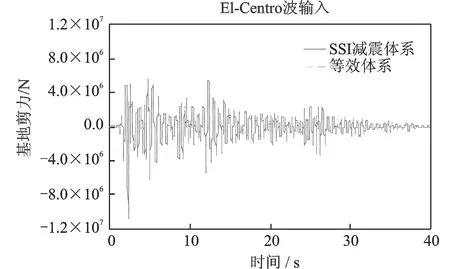
图13 等效体系与原结构体系基底剪力对比(Vs=300 m/s)Fig.13 Comparison of base shear force between equivalent system and the original system(Vs=300 m/s)

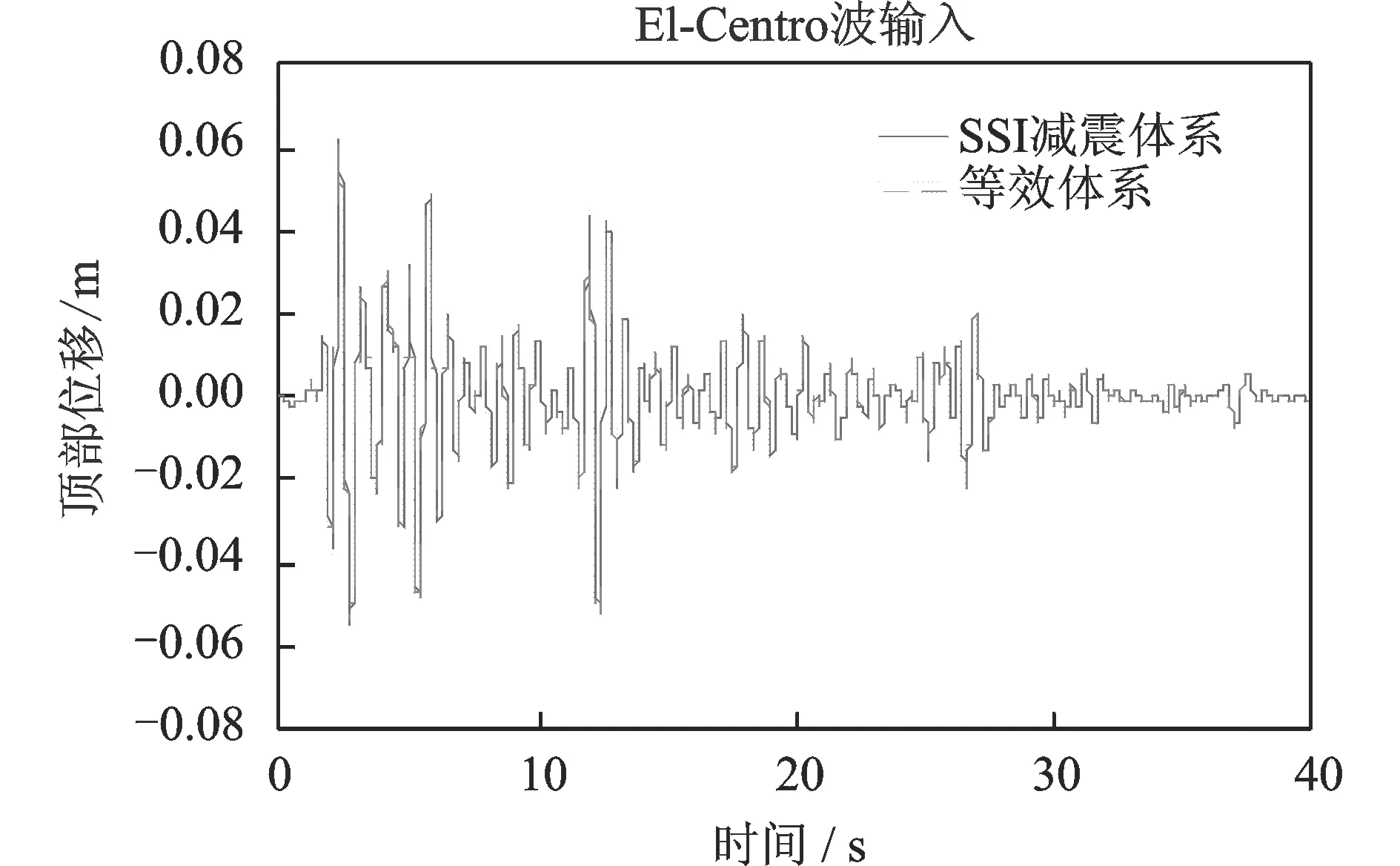
图14 等效体系与原结构体系顶部位移对比(Vs=100 m/s)Fig.14 Comparison of top displacement between equivalent system and the original SSI system(Vs=100 m/s)

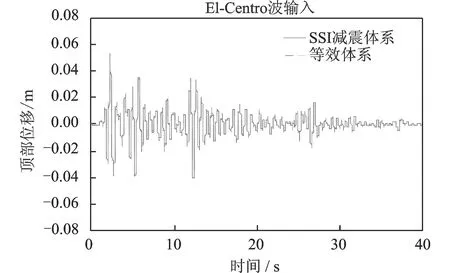
图15 等效体系与原结构体系顶部位移对比(Vs=300 m/s)Fig.15 Comparison of top displacement between equivalent system and the original SSI system(Vs=300 m/s)

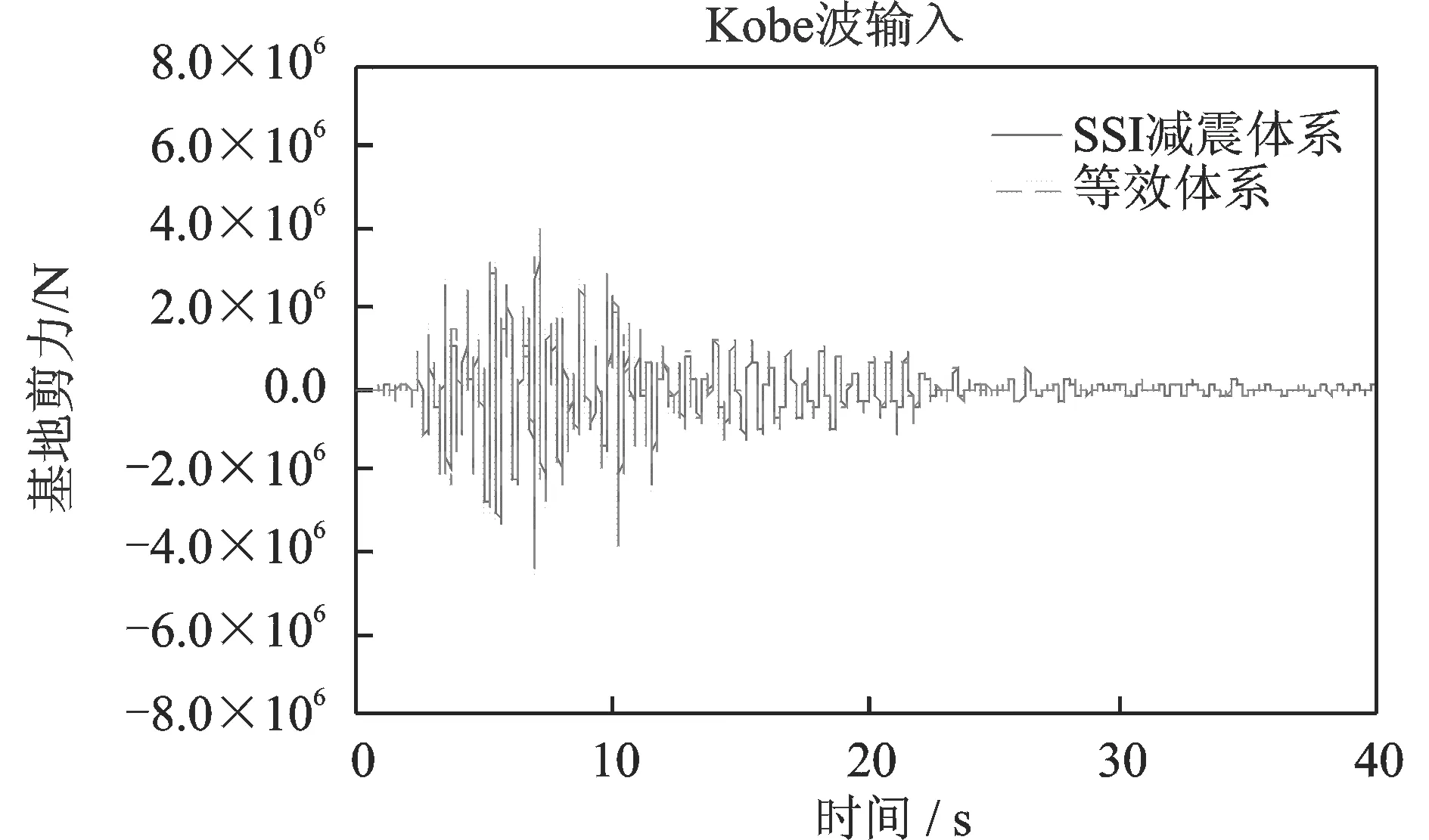
图16 等效体系与原结构体系基底剪力对比(Vs=100 m/s)Fig.16 Comparison of base shear force between equivalent system and the original SSI system(Vs=100 m/s)

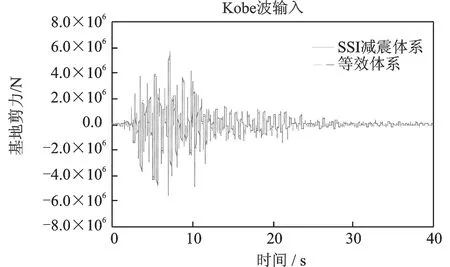
图17 等效体系与原结构体系基底剪力对比(Vs=300 m/s)Fig.17 Comparison of base shear force between equivalent system and the original system(Vs=300 m/s)

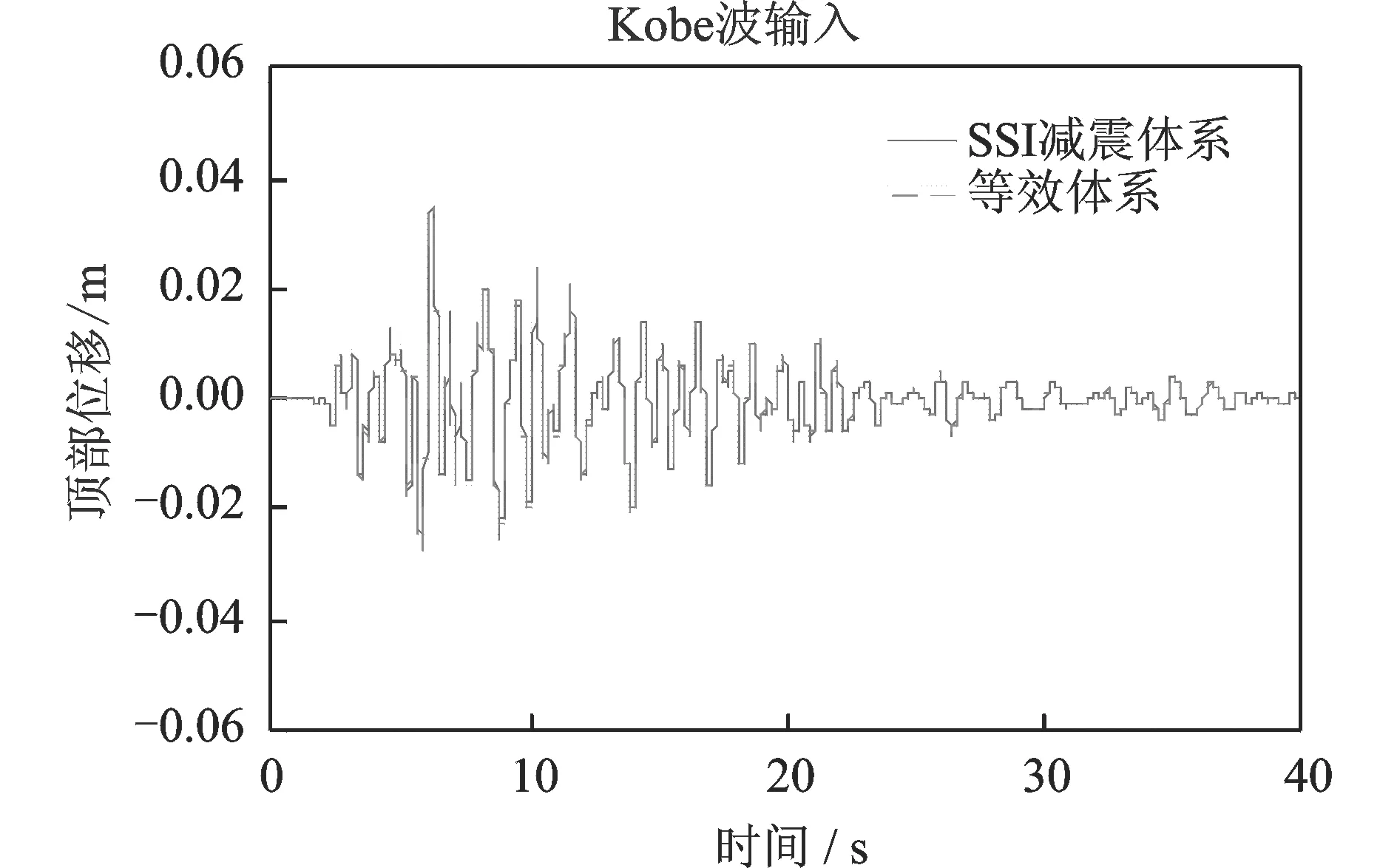
图18 等效体系与原结构体系顶部位移对比(Vs=100 m/s)Fig.18 Comparison of top displacement between equivalent system and the original SSI system(Vs=100 m/s)

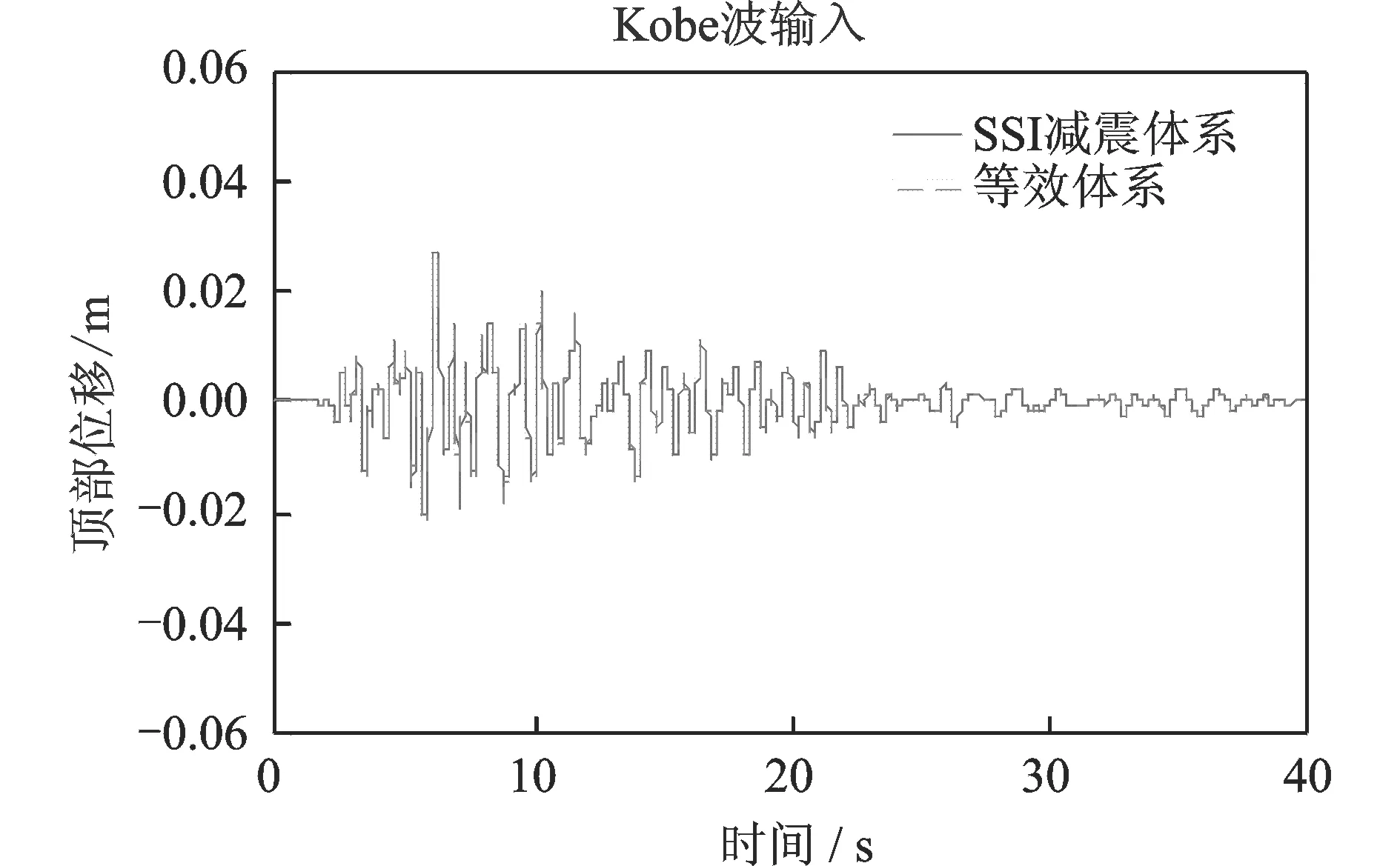
图19 等效体系与原结构体系顶部位移对比(Vs=300 m/s)Fig.19 Comparison of top displacement between equivalent system and the original SSI system(Vs=300 m/s)

6 结束语

本文通过结合模态应变能法与单自由度黏弹性减震结构体系的传递函数，推导出了能够考虑SSI效应的体系等效周期及等效阻尼比的计算方法，并进行了相应的参数化分析。通过多质点体系的等效方法，将该简化方法应用到质量刚度分布比较均匀的以第一振型为主的减震框架结构体系。算例表明该方法具有一定的精度，对考虑SSI效应的黏弹性减震框架结构的抗震评估具有一定的工程应用价值。

[1] 周福霖. 工程结构减震控制[M]. 北京: 地震出版社, 1997.

ZHOU Fu-lin. Seismic Control in Engineering Structures[M]. Beijing: Seismological Press, 1997.

[2] Housner G W, Bergman L A, Caughey T K, et al. Structural control: past, present, and future[J]. Journal of Engineering Mechanics, 1997, 123(9): 897—971.

[3] Powell G H, Allahabad A. Seismic damage prediction by deterministic method: concept and procedures[J]. Earthquake Engineering and Structural Dynamics, 1988, 16(5): 719—734.

[4] 宋和平, 吕西林. 土体-结构相互作用对消能减震结构的影响[J]. 地震工程与工程振动, 2009, 29(1):162—168.

SONG He-ping, LÜ Xi-lin. Influence of soil-structure-interaction on energy dissipating structures[J]. Earthquake Engineering and Engineering Vibration , 2009, 29(1): 162—468.

[5] 张兆超. 土-结构动力相互作用在消能减震控制中的作用探讨与研究[D]. 长沙: 湖南大学，2009.

ZHANG Zhao-chao. The research and discussion on the role of soil-structure dynamic interaction in the control of energy dissipation[D]. Changsha: Hunan University, 2009.

[6] N Makris, M C C Constantinou. Fractional derivative Maxwell model For viscous dampers[J]. Journal of Structure Engineering, ASCE, 1991: 117:2708—2724.

[7] 日本建築学会.入門·建物と地盤動との相互作用[M].东京：東京日本建築学会,1996.

[8] Zambrano A. Modal coupling and accuracy of modal strain energy method[J]. Journal of Engineering Mechanics, 1996, 122(7):603—612.

[9] Chopla AK. Dynamic of Structures. Theory and Applications to Earthquake Engineering[M]. NJ: Prentice-Hall, 2011.

[10]Kausel E, Ushijima R. Vertical and torsional stiffness of embedment footings[R]. Research Report R79-6, Massachusetts Institute of Technology, 1979.

[11]周云. 黏弹性阻尼减震结构设计[M]: 武汉: 武汉理工大学出版社, 2006.

ZHOU Yun. Viscoelastic Damping Structure Design[M]. Wuhan: Wuhan University of Technology Press, 2006.

[12](日)社团法人. 被动减震结构设计、施工手册[M]. 北京：中国建筑工业出版社, 2008.

A simplified design method for structures with viscoelastic dampers
considering soil-structure dynamic interaction effect

ZHAOXue-fei,WANGShu-guang,DUDong-sheng,LIUWei-qing

(College of Civil Engineering, Nanjing Tech University, Nanjing 210009, China)

The dynamic equilibrium equation for single-degree-of-freedom (SDOF) structure with viscoelastic dampers considering soil-structure interaction (SSI) effect is firstly established in frequency domain, then the equivalent period and damping are obtained through the combination of modal stain energy (MSE) method and the transfer function of the system. Parametric analysis is also conducted to study the SSI influence on the efficiency of the dampers, the results show that the slenderness ratio of the structure and the initial additional damping have a significant influence on the efficiency of the dampers. The proposed simple method is also used to multi-degree-of-freedom (MDOF) frame energy dissipating structures with relatively uniform mass and stiffness distribution. The numerical results demonstrate that this method has a good accuracy, which has an available application value in the evaluation of energy dissipating structures considering SSI effect.

soil-structure interaction; damping structure; viscoelastic damper; equivalent method

2015-08-23；

2016-05-27

国家自然科学基金重大研究计划资助项目(90815017)；国家自然科学基金资助项目(51678302，51678301)

TU352.12；TU311.3

：A

1004-4523(2016)06-1079-09

10.16385/j.cnki.issn.1004-4523.2016.06.018

赵学斐(1987—)，男，博士研究生。电话：15850573187；E-mail:zhaoxuefeinjut@163.com

王曙光(1972—)，男，教授,博士生导师。电话：13584029545；E-mail:720108@vip.sina.com