基于改进变分模态分解的旋转机械故障时频分析方法①

刘尚坤， 唐贵基， 王晓龙

(华北电力大学机械工程系， 河北 保定 071003)

基于改进变分模态分解的旋转机械故障时频分析方法①

刘尚坤， 唐贵基， 王晓龙

(华北电力大学机械工程系， 河北 保定 071003)

变分模态分解(variational mode decomposition, VMD)算法作为一种新的多分量信号分解方法，采用频域迭代的求解方式，具有明确的理论基础和高的分解精度，为了自适应确定其分解分量的个数，以互信息为判据对原方法进行了迭代停止条件的改进，并结合Teager能量算子具有对单分量信号解调速度快、精度高的优点，提出了Teager-VMD时频分析新方法。仿真信号分析表明该方法能将含有变频、频率突变和频率相近的多分量信号进行有效的分离；实测转子系统局部碰摩、油膜振荡信号分析表明，该方法能够精确提取各分量的清晰时频特征，能准确地辨别碰摩故障的严重程度和诊断油膜振荡故障，较HHT方法精确有效，具有一定的工程应用价值。

故障诊断；时频分析； 碰摩；Teager能量算子； 油膜振荡

引 言

汽轮机等旋转机械由于结构复杂、工况多变，故障振动信号常表现为多分量非平稳特点。由于时频分析方法能同时提供非平稳信号在时域和频域的局部化信息而得到了广泛的应用[1-6]，而对多分量信号分析的关键是找到一种有效的信号分解方法[1]。针对这一问题学者们进行了不断的探索，文献[2]利用希尔伯特-黄变换(Hilbert-Huang Transform，HHT)分析和监测裂纹转子的瞬态响应，文献[3]利用建立在EMD基础上的Teager-Huang对转子碰摩故障进行了诊断，但由于EMD存在模式混淆、过包络、欠包络等问题[4]影响分析效果；文献[5]利用经验小波变换(Empirical Wavelet Transform, EWT)分析了碰摩故障的频率分布以判别碰摩故障的严重程度；文献[6]采用希尔伯特振动分解(Hilbert Vibration Decomposition，HVD)诊断了转子系统油膜涡动故障。

Dragomiretskiy等提出了一种新的多分量信号自适应分解方法——变分模态分解(VMD)[7]，该方法采用频域非递归的迭代求解方式搜寻变分模型最优解来确定每个调幅调频分量的中心频率及带宽，最终自适应的实现信号的频域剖分及各分量的分离，分解精度高且能有效避免模式混淆问题[8]。文献[9]利用VMD分解得到的中心频率作为聚类中心并结合标准模糊C均值聚类诊断了滚动轴承故障。本文在介绍VMD算法的基础上，提出基于互信息准则的自适应确定变分模态分解分量个数的改进算法，并与Teager能量算子解调相结合，提出了Teager-VMD时频分析新方法，仿真信号和实测转子局部碰摩、油膜失稳信号分析效果说明了该方法的有效性。

1 Teager-VMD时频分析方法原理

1.1 变分模态分解

变分模态分解将本征模态函数(IMF)定义为一个调幅调频信号，即

uk(t)=Ak(t)cos[φk(t)]

(1)

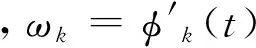
假设原信号f为多分量信号，由K个有限带宽的本征模态函数(IMF)分量uk组成，且各IMF的中心频率为ωk，VMD算法建立的约束变分模型为

(2)

式中 uk={u1, … ,uK}，ωk={ω1, …,ωK}。

该模型中，通过Hilbert变换得到uk(t)的解析信号进而得到单边谱,乘以指数函数e-jωkt是将所估计的uk(t)的中心频带调整到基频带上，为求上述约束变分问题的最优解，需将其转换为非约束变分问题，为此引入如下形式的增广Lagrange函数

(3)

式中 α为二次项惩罚参数；λ为Lagrange乘子。利用乘子交替方向算法不断更新各IMF及其中心频率，最终所求式(3)的鞍点即为原问题的最优解，而所有的IMF可从频域中通过下式获得

(4)

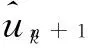
(5)

1.2 VMD分量个数的自适应确定

由VMD算法原理可知，其处理信号时需要预先设定分解IMF分量的个数K，然而受不同设备不同工况的限制，K值通常难以准确设定。为解决这一问题，本文利用互信息为判据来控制VMD算法的迭代过程，提出自适应确定分量个数K的改进VMD算法。

互信息(mutual information，MI)由信息论中熵的概念引申而来，用两个随机变量间不确定度的差值表示，能够表明其统计相关性，比相关系数法更准确[10]，能更好地辨别相关程度。互信息表达式如下

MI(X,Y)=H(Y)-H(Y|X)

(6)

式中H(Y)为Y的熵，H(Y|X)为已知X时Y的条件熵。

上式表明，X与Y的相关性越强，条件熵值H(Y|X)越小，则互信息MI(X,Y)越大[11]，本文将其由下式

δi=MIi/max(MIi)

(7)

进行归一化后，用于判断分解余量与原信号的相关程度，当归一化互信息值低于阈值(参考文献[10]，本文取阈值δ=0.02)时，认为分解余量不再含有重要信息，原信号已被完全分解，结束整个运算过程，从而能够根据实际分析信号自动地确定IMF分量的个数，具体实现步骤如下：

(1) 初始化K为1；

(2)K=K+1，执行外层循环；

(4) n=n+1，开始内层循环；

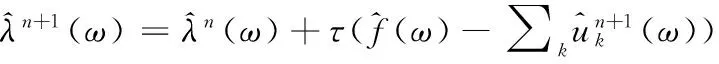
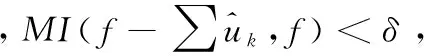
1.3 Teager能量算子解调

本研究针对当前应用型心理学课程教学存在的弊端，在心理卫生学教学中，整合合作学习和探究性学习两种学习方式，以学生学习小组为单位，结合相关教学内容，通过探究性学习，研究和解决实际心理问题，深化学生对心理卫生学理论的理解，培养学生的心理卫生学应用能力。

要表达K个分量的时频分布信息，还需对得到的每个IMF分量进行解调分析，Teager能量算子是一种非线性差分算子，解调能力比Hilbert变换解调能力强[12]，同时具有时间分辨率高、解调速度快的优点，能够对单分量的调幅调频信号解调[13]，近些年被广泛用于信号解调分析[14-15]。

对于调幅调频的连续时间信号x(t)，其Teager能量算子定义为

(8)

对应离散信号x(n)的能量算子定义为

ψ[x(n)]=x2(n)-x(n+1)x(n-1)

(9)

由式(9)可知每一时刻算子的计算只需要3个样本数据，计算量较小，由式(10)和(11)实现单分量调幅调频信号的瞬时频率与瞬时幅值的求解。

(10)

(11)

相对于Hilbert变换，Teager能量算子在求信号的瞬时频率时，无需进行复数计算，具有快速响应能力，可以迅速跟踪瞬时变化信号的幅值和频率，能更好地揭示瞬时频率的突变情况。

1.4 Teager-VMD时频分析方法

本文提出的Teager-VMD时频分析方法，首先利用改进VMD算法自适应将一多分量信号分解为K个表征信号特征的IMF分量(同时参考文献[7],本文设定惩罚参数α=300)，再通过Teager能量算子计算每个IMF分量的瞬时幅值和瞬时频率，得到原信号的时频分布信息，最后通过分析时频分布图中的故障特征频率诊断故障类型。基于改进变分模态分解的机械故障时频分析方法的分析流程如图1所示。

图1 Teager-VMD时频分析流程图Fig.1 Teager-VMD time-frequency analysis flow chart

具体实现步骤如下：

(2)通过Teager能量算子解调计算每一个IMF分量的瞬时幅值和瞬时频率。

(3)绘制三维时频分布图，分析其中是否存在相应的故障特征频率，进而判断故障类型，实现故障诊断。

2 仿真信号分析

利用仿真信号来验证本文方法的时频分析能力,考查一含有噪声的多分量信号x(t)，其中分量x1(t)为调幅调频信号，x2(t)是在两个不同时间段频率单一的频率突变信号，x3(t)是频率接近的两个余弦信号，x4(t)是噪声模拟信号。具体表达式如下式

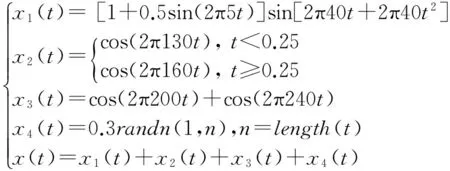
(12)

采样频率为2048 Hz，分析点数为1024点。图2为多分量信号x(t)的时域波形。首先，利用改进VMD算法对x(t)进行分解，得到5个IMF分量，如图3所示，图中各个分量被较好地分解出来，各个IMF与原信号的归一化互信息如表1所示，其中前4个分量大于阈值0.02。图4是对前4个IMF分量进行能量算子解调得到的时频分布图，由图可知，VMD能较好的把调幅调频分量x1(t)、频率突变分量x2(t)以及x3(t) 中频率接近的200与240 Hz分量进行有效分离，清晰地表示了各分量的时频信息。

为了对比分析，图5是采用HHT分析该仿真信号得到的Hilbert谱，由图可知，各分量频率调制现象明显，分解得到的调幅调频分量x1(t)不够明确，频率突变分量x2(t)中的130 Hz分量尚能基本识别，而160 Hz分量不能识别，x3(t)中两个频率接近的分量不能有效分离，效果较本文方法差。

图2 仿真信号的时域波形Fig.2 Time domain waveform of simulation signal

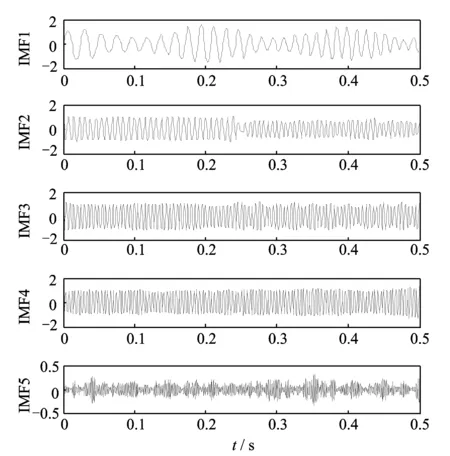
图3 仿真信号的自适应变分模态分解Fig.3 Adaptive variational mode decomposition of simulation signal

表1 各IMF与仿真信号的归一化互信息值

Tab.1 Normalized mutual information value between IMFS and simulation signal

IMF1IMF2IMF3IMF4IMF50.90130.74901.00000.88720.0003

图4 仿真信号的Teager-VMD时频分布图Fig.4 Teager-VMD time-frequency distribution of simulation signal

图5 仿真信号HHT分析的Hilbert谱Fig.5 Simulation signal′s Hilbert spectrum by HHT

3 转子实验振动信号分析

实验装置采用Bently RK-4转子系统故障模拟实验台(如图6所示)，配有信号前置适配器、转速控制调节装置和做油膜失稳所需的轴承、油泵系统。在单盘转子两侧安装电涡流传感器测量转轴径向振动位移，由美国Iotech 公司生产的 ZonicBook/618E设备采集转子在碰摩过程中以及在油膜失稳状态下的振动信号，采样频率为1280 Hz，本文取转子各实验状态的1280个采样点加以分析。

图6 转子实验台Fig.6 Rotor experiment platform

3.1 碰摩故障分析

在距离转轴小间隙处由支架固定一铜质顶针，转轴升速过程中与铜质顶针发生局部碰摩，随着转速的升高局部碰摩程度由轻微发展到严重，采集振动信号进行分析。

图7是转速为1 560 r/min时采集的轻微碰摩信号的时域波形和频谱图，从时域波形上基本上看不出发生了碰摩故障，频谱图中也只是转频26 Hz幅值明显，难以判断已经发生了碰摩故障。

图7 轻微碰摩信号的时域波形和频谱图Fig.7 Time domain waveform and spectrum of slight rub-impact signal

图8 轻微碰摩信号的自适应变分模态分解Fig.8 Adaptive variational mode decomposition of slight rub-impact signal

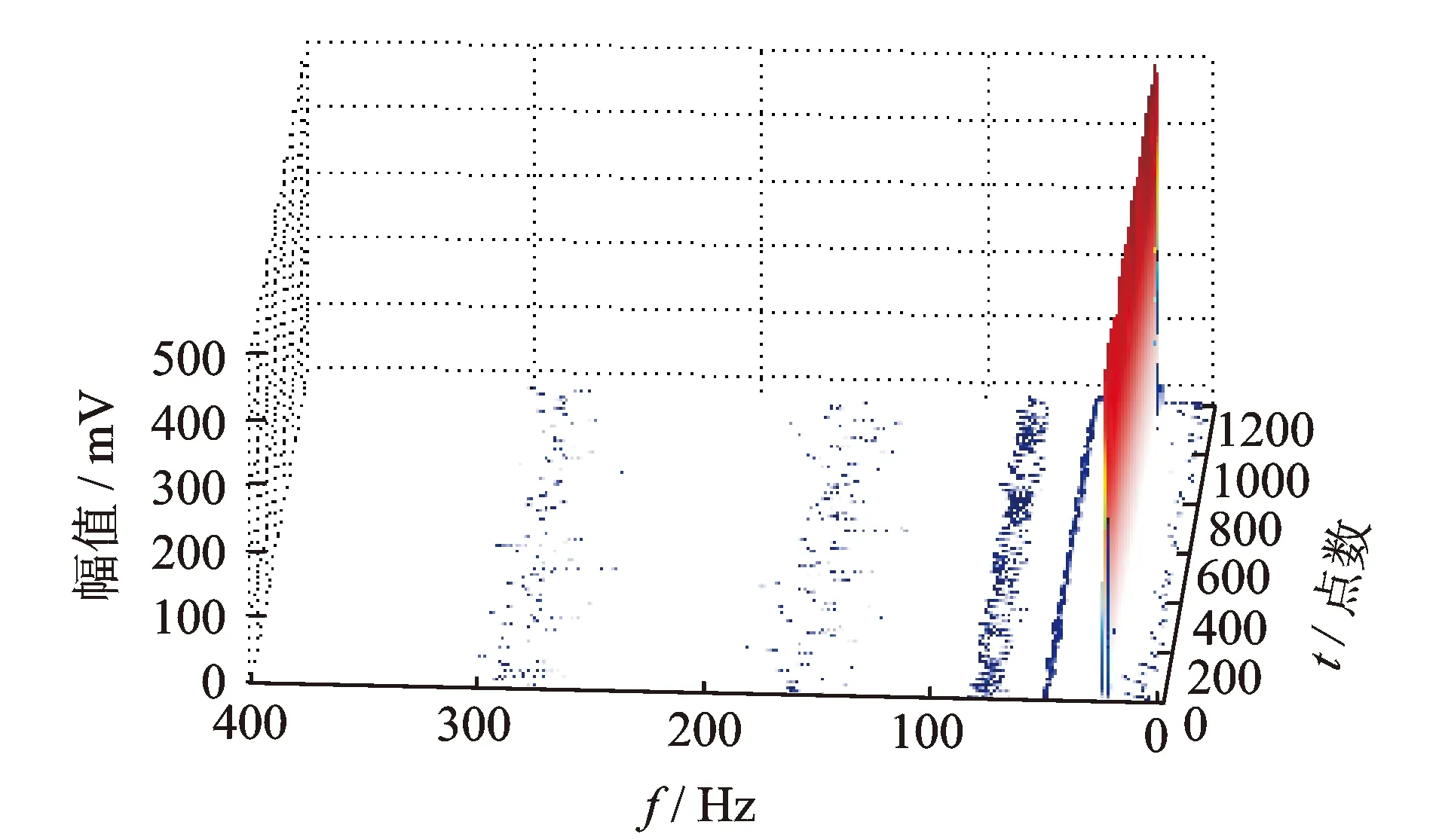
图9 轻微碰摩信号的Teager-VMD时频分布图Fig.9 Teager-VMD time-frequency distribution of slight rub-impact signal

图8是采用改进VMD分解得到的8个IMF分量，周期性明显的分量中，IMF7对应转频，IMF4对应二倍频，IMF3对应三倍频。对大于阈值的前7个IMF分量进行Teager能量算子解调得到图9所示的轻微碰摩信号的Teager-VMD时频分布图，图中转频幅值最大，同时存在幅值较小的二倍频、三倍频成分，也存在幅值很小且频率波动的三分频及高次谐波，通过分析，结合碰摩故障特征[16]可以准确地确定转子已经发生了碰摩且程度轻微，实现了早期转子碰摩故障的识别。

为了对比本文方法的分析效果，图10是将轻微碰摩信号进行HHT分析得到的Hilbert谱，图中只能分析出转频具有频率调制特点，难以准确地判断一定发生了碰摩故障，相比本文分析方法较差。

图10 轻微碰摩信号HHT分析的Hilbert谱Fig.10 Slight rub-impact signal′s Hilbert spectrum by HHT

图11是转速为1740 r/min时采集的严重碰摩信号时域波形和频谱图，图中幅值变大说明碰摩程度及能量变大，时域波形中已经发生了较明显的变形，频谱图中仍是转频29 Hz幅值突出，但能够观察到小幅值的二倍频、三倍频成分。该信号的自适应变分模态分解如图12所示，共得到11个IMF分量，分量间存在着倍频特征，对大于阈值的前10个IMF分量做能量算子解调得到的时频分布图如图13所示，图中各分量的时频谱清晰可见，其中2～7倍频成分被准确检测出来，且2～4倍频幅值相对较大，5～7倍频幅值相对较小，同时图中还有10倍频的调制频率成分出现，此频谱特征充分表明转子发生了严重的碰摩故障。

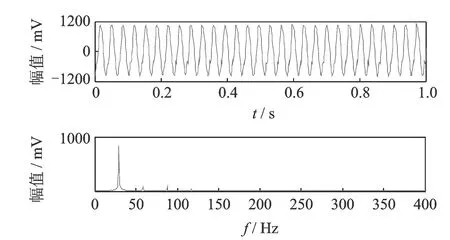
图11 严重碰摩信号的时域波形和频谱图Fig.11 Time domain waveform and spectrum of serious rub-impact signal

图12 严重碰摩信号的自适应变分模态分解Fig.12 Adaptive variational mode decomposition of serious rub-impact signal

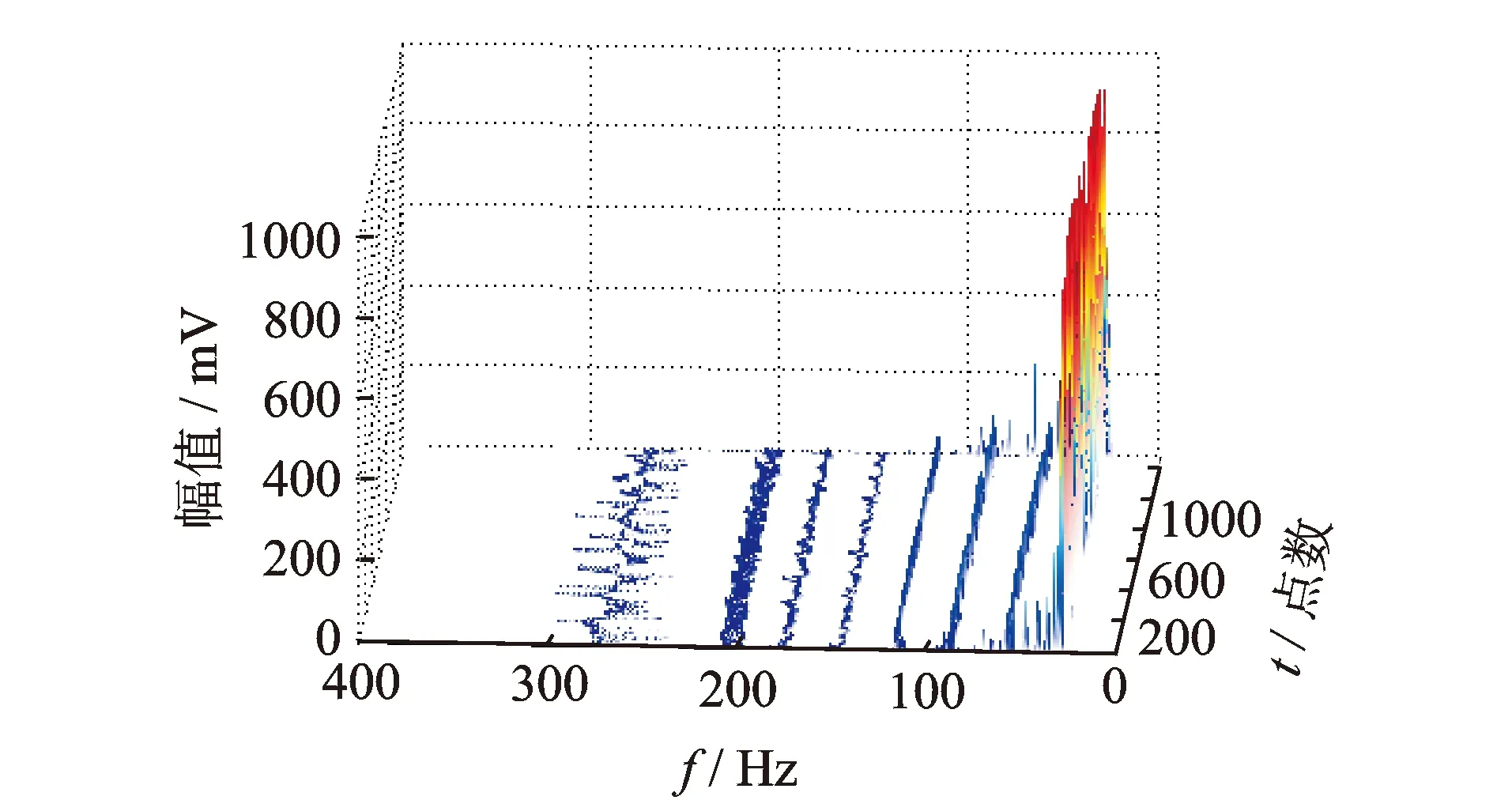
图13 严重碰摩信号的Teager-VMD时频分布图Fig.13 Teager-VMD time-frequency distribution of serious rub-impact signal

为了对比分析，图14是将严重碰摩信号进行HHT分析得到的Hilbert谱，图中虽能显示出被调制的转频29 Hz及高频成分，但不能详细分析各频率特征，对碰摩的严重程度不易准确辨别，分析效果明显不如本文分析效果。

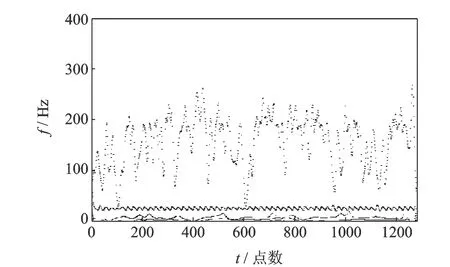
图14 严重碰摩信号HHT分析的Hilbert谱Fig.14 Serious rub-impact signal′s Hilbert spectrum by HHT

3.2 油膜失稳故障分析

转子系统油膜失稳常由半速油膜涡动发展为油膜振荡[17]，由于油膜振荡的频谱结构较油膜涡动复杂，下面分析实验台转子1阶油膜振荡时的频谱特征。

图15 油膜振荡信号的时域波形和频谱图Fig.15 Time domain waveform and spectrum of oil-whip

图16 油膜振荡信号的自适应变分模态分解Fig.16 Adaptive variational mode decomposition of oil-whip

图17 油膜振荡信号的Teager-VMD时频分布图Fig.17 Teager-VMD time-frequency distribution of oil-whip

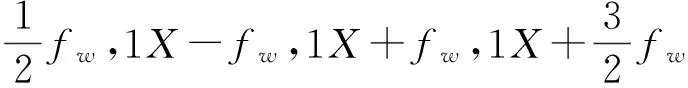
为了进行分析效果对比，图18是采用HHT分析油膜振荡信号得到的Hilbert谱，图中800～1000采样点时段出现了明显的频率混淆现象，虽然分析出振荡频率31 Hz及其二分频成分，但转频76 Hz出现明显的调制现象，其他组合频率也不能分解出来，比本文方法分析效果差。

图18 油膜振荡信号HHT分析的Hilbert谱Fig.18 Oil-whip signal′s Hilbert spectrum by HHT

4 结 论

(1)结合变分模态分解与Teager能量算子解调各自的优点，本文提出了一种Teager-VMD时频分析方法。为了在信号分解过程中自适应地确定VMD分量的个数，采用互信息准则对VMD的迭代停止条件进行了改进，实现了分量个数的自适应确定。对比分析表明该方法效果明显优于HHT方法，具有一定的工程应用价值。

(2)将Teager-VMD时频分析方法应用于转子实验信号，精确地分析出转子轻微碰摩和严重碰摩时的频率成分以及油膜振荡时的转频、振荡频率及其和差组合频率成分，准确地诊断了故障，也表明该方法提取信号时频特征的精确性和准确性。

(3)本文仅对单盘转子的局部碰摩及油膜振荡现象进行了时频分析与故障诊断，取得了较好的效果，所提方法在其他复杂设备、复杂工况及其他行业领域中的应用有待进一步研究。

[1] 程军圣, 杨宇, 于德介. 基于广义解调时频分析的多分量信号分解方法[J]. 振动工程学报, 2007, 20(6):563—569.

CHENG Junsheng, YANG Yu, YU Dejie. A multi component signal decomposition method based on the generalized demodulation time frequency analysis[J]. Journal of Vibration Engineering, 2007, 20(6):563—569.

[2] Ramesh Babu T, Srikanth S, Sekhar A S. Hilbert-Huang transform for detection and monitoring of crack in a transient rotor [J]. Mech. Syst. Signal Process, 2008, 22 (4): 905—914.

[3] Liu Shangkun，Tang Guiji，Pang Bin. Rotor local rubbing fault feature analysis based on Teager-Huang transform [C]. 4th International Conference on Materials Science and Information Technology, Tianjin, China, 2014：3244—3247.

[4] 向玲，鄢小安. 汽轮机转子故障诊断中LMD法和EMD法的性能对比研究[J]. 动力工程学报, 2014, 34(12): 945—951.

XIANG Ling, YAN Xiaoan. Performance contrast between LMD and EMD in fault diagnosis of turbine Rotors [J]. Journal of Chinese Society of Power Engineering, 2014, 34(12): 945—951.

[5] 李志农，朱明，褚福磊，等. 基于经验小波变换的机械故障诊断方法研究[J]. 仪器仪表学报，2014, 35(11): 2423—2432.

LI Zhinong, ZHU Ming, CHU Fulei, et al. Mechanical fault diagnosis method based on empirical wavelet transform [J]. Chinese Journal of Scientific Instrument, 2014, 35(11): 2423—2432.

[6] 唐贵基，庞彬. 基于改进的希尔伯特振动分解的机械故障诊断方法研究[J]. 振动与冲击，2015, 34(3): 167—171.

Tang Guiji, Pang Bin. Research for a mechanical fault diagnosis method based on improved Hilbert vibration decomposition [J]. Journal of Vibration and Shock, 2015, 34(3): 167—171.

[7] Dragomiretskiy Konstantin, Zosso Dominique. Variational mode decomposition [J]. IEEE Transactions on Signal Processing，2014，62(3): 531—544.

[8] 唐贵基，王晓龙. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J]. 西安交通大学学报，2015,49(5): 73—81.

TANG Guiji, WANG Xiaolong. Parameter optimized variational mode decomposition method with application to incipient fault diagnosis of rolling bearing [J]. Journal of Xi′an Jiaotong University, 2015, 49(5):73—81.

[9] 刘长良, 武英杰, 甄成刚. 基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断[J]. 中国电机工程学报, 2015, 35(13): 3358—3365.

LIU Changliang, WU Yingjie, ZHEN Chenggang. Rolling bearing fault diagnosis based on variational mode decomposition and fuzzy c means clustering [J]. Proceedings of the CSEE, 2015, 35(13): 3358—3365.

[10]胡爱军． Hilbert-Huang 变换在旋转机械振动信号分析中的应用研究[D]．保定：华北电力大学, 2008．

Hu Aijun． Research on the application of Hilbert-Huang Transform in vibration signal analysis of rotating machinery [D]．Baoding, North China Electric Power University, 2008.

[11]张志刚，石晓辉，施全，等. 基于改进EMD和谱峭度法滚动轴承故障特征提取[J]. 振动、测试与诊断, 2013, 33(3): 478—530.

Zhang Zhigang, Shi Xiaohui, Shi Quan, et al. Fault feature extraction of rolling element bearing based on improved emd and spectral kurtosis [J]．Journal of Vibration，Measurement & Diagnosis，2013, 33(3): 478—530.

[12]钟先友.旋转机械故障诊断的时频分析方法及其应用研究[D]．武汉：武汉科技大学，2014．

Zhong Xianyou. Research on time-frequencyanalysis methods and its applications to rotating machinery fault diagnosis[D]．Wuhan：Wuhan University of Science and Technology，2014．

[13]Marago S P，Kaiser J F，Quatieri T F．Energy separation in signal modulations with applications to speech analysis [J]．IEEE Transactions on Signal Processing，1993，41(10)：3024—3051．

[14]孟宗, 李姗姗, 季艳. 基于对称差分能量算子解调的局部均值分解端点效应抑制方法[J]. 机械工程学报, 2014, 50(13): 80—87.

MENG Zong, LI Shanshan, JI Yan. Restraining method for end effect of local mean decomposition based on energy operator demodulation of symmetrical differencing[J]. Chinese Journal of Mechanical Engineering , 2014, 50(13): 80—87.

[15]张文义，于德介，陈向民．齿轮箱复合故障诊断的信号共振分量能量算子解调方法[J]．振动工程学报，2015，28(1)：148—155．

Zhang Wenyi，YU Dejie，Chen Xiangmin．Energy operator demodulating of signal′s resonance components for the compound fault diagnosis of gearbox [J]. Journal of Vibration Engineering, 2015，28(1)：148—155．

[16]马辉, 杨健, 宋溶泽, 等. 转子系统碰摩故障实验研究进展与展望[J]. 振动与冲击, 2014, 33(6): 1—12.

MA Hui, YANG Jian, SONG Rongze, et al. Review and prospect on the research of rub-impact experiment of rotor systems [J]. Journal of Vibration and Shock, 2014, 33(6): 1—12.

[17]唐贵基，向玲，朱永利. 基于 HHT的旋转机械油膜涡动和油膜振荡故障特征分析[J]. 中国电机工程学报，2008, 28(2):77—81.

TANG Guiji, XIANG Ling, ZHU Yongli. Fault analysis of oil whirl and oil whip based on Hilbert Huang transform for rotor system [J]. Proceedings of the Chinese Society for Electrical Engineering, 2008, 28(2): 77—81.

[18]马辉，李辉，唐玉生，等. 两种不同载荷形式下转子系统油膜失稳的数值研究[J]. 振动工程学报，2013, 26(1): 105—111.

MA Hui, LI Hui, TANG Yusheng, et al. Numerical research on oil-film instability in a rotor system under two types of load conditions [J]. Journal of Vibration Engineering, 2013, 26(1): 105—111.

Time frequency analysis method for rotary mechanical fault based
on improved variational mode decomposition

LIUShang-kun,TANGGui-ji,WANGXiao-long

(School of Mechanical Engineering，North China Electric Power University, Baoding 071003, China)

As a new method for multi-component signal's decomposition, variational mode decomposition (VMD) has explicit theoretical basis and high decomposition accuracy. In order to adaptively determine the number of its decomposition components, the criterion of mutual information is used to improve the iterative stopping conditions to the original method. Combining with the advantages of fast and high accuracy of Teager energy operator demodulation, a new method named Teager-VMD is proposed for time frequency analysis. The simulation signal analysis results show that the proposed method can effectively separate the multi-component signal with frequency conversion, frequency mutation and frequency similar signal. The analysis results of the local rub-impact and oil whip of the experiment rotor system show that the proposed method can accurately extract the clear time-frequency characteristics and can accurately identify the severity of the rub-impact fault and diagnosis the oil whip fault. The proposed method is more accurate and effective than the HHT method and has certain engineering application value.

fault diagnosis; time frequency analysis; rub-impact; Teager energy operator; oil whip

2015-10-21；

2016-02-28

国家自然科学基金资助项目(51307058，51475164)；河北省自然科学基金资助项目(E2014502052, E2015502013)；中央高校基本科研业务费专项资金资助项目(2014MS156，2015XS120)

TH165+.3；TN911.7

1004-4523(2016)06-1119-08

10.16385/j.cnki.issn.1004-4523.2016.06.022

刘尚坤(1979—)，男，博士研究生，讲师。电话：(0312)7523442; E-mail:lsk1213@163.com

唐贵基(1962—) ,男, 教授, 博士生导师。电话:(0312)7525028; E-mail:tanggjlk@ncepubd.edu.cn