事件驱动无线传感器网络中有效节点的选择方法

朱旻如 郭 剑

(南京邮电大学计算机学院 江苏 南京 210003)

事件驱动无线传感器网络中有效节点的选择方法

朱旻如 郭 剑

(南京邮电大学计算机学院 江苏 南京 210003)

事件驱动的无线传感器网络需要对事件状态做出合理的判断以进行处理，本文研究如何选取少量节点参与通信，以较低的能耗代价获取事件状态。文中提出的NSS(Node Supported Selection)算法，首先利用节点之间的空间相关性将事件感知空间划分为若干相关单元，再依据节点支持度选取代表节点参与数据传输。仿真结果表明，该算法只需小比例的节点数就能保证感知精度，且具有较好的可扩展性，能满足多样的应用需求。

事件驱动无线传感器网络；环状空间相关性；最优节点集选择；节点支持度；失真度

1.引言

WSN(Wireless Sensor Networks)因其能满足战场监控、灾难管理、环境监测、智能家居、健康管理等特殊环境而日益受到重视，但是WSN节点多是微小的，能量、存储和处理能力有限，该现状造成对WSN的研究存在很多约束，诸如能耗限制、计算能力和存储能力限制等，而能耗的控制更是首当其冲的设计要素[1-2]。WSN依赖网内各个节点的协作共同完成任务，各个节点不仅需要感知周边信息并及时向sink传输，往往还需要作为中继节点帮助形成有效的传输路径。节点之间的协同合作有利于提高感知精度、增强覆盖范围，及对事态做出正确评估等[3]。

然而，为增强整个网络的连通性和鲁棒性，节点通常是密集部署，大量的被感知数据在网内传递也造成能耗的急剧增加，甚至信道的竞争和拥塞，这都不利于网络的持续和稳定。近年研究者利用密集分布的节点之间感知的信息具有空间相关性特点展开了研究。文献[4-5]采用数据融合技术，感知的数据延路由向sink传递经过融合节点时进行融合计算，减少冗余数据，从而减轻无线链路和基站的通信开销；文献[6-9]从密集分布的节点中选取部分节点参与数据的传输，在保证数据精度的同时也能大大降低网内传输的数据总量。文献[10-11]利用DSC（Distributed Source Coding）消除数据之间的冗余。文献[10]在信道编码的思想上考虑空间相关性以分割信源的符号空间，使得通信时只需要传递信源所在陪集的索引就可以 完成信息传递，大大减低能耗。

在事件驱动的无线传感器网络如森林火灾检测、目标跟踪等应用中，研究者更关注的在一定误差容忍范围内对事件做出及时有效的处理而不是数据的无损传递[12][13]，因此，当有突发事件产生时，从感知到事件的节点中选取部分具有代表性节点参与数据传输，尽量以较低的能耗代价使得sink节点在接收到数据后能对事件做出有效正确的评估，该问题是值得研究的。文献[8]中M.C.Vuran等在时间和空间相关性的模型基础上，依据节点分布的统计属性给出部分节点参与感知来保证事件感知的精度，所采用的随机节点选取方法经过验证显示尽管随着节点的加入失真度逐步降低，但随机选择的节点不一定具有很好的代表性[8]。随后又进一步提出INS(Interative Node selection)算法选择节点集，用矢量量化算法将节点投影到Voronoi空间，再根据感知半径选取一定的代表节点以保证失真度要求，但是过程中没有考虑事件源的位置对代表节点选择的影响[14]。文献[15]改进了失真度判断方法，用AOST(Adaptive Add One Sensor node at a Time)算法逐个选取节点加入传输节点集，算法简单且性能上有较大提高，但是每一轮选取节点时都需要对感知范围内的所有节点进行遍历，大大增加了运算工作量和计算时间。和本文相似的研究如苏威等也提出了环状相关性模型并验证其可行性，但是并没有就此给出代表节点选择的方法[16]。

本文将在文献[8]基础上考虑到节点之间的相关性不仅和节点之间的距离有关，还和节点到事件源的距离有关，得到环状相关性模型，在此基础上提出NSS（Node Supported Selection）算法，将事件感知空间划分为若干相关单元，从每个相关单元选取一个代表节点，这些代表节点协作参与数据传输，通过调整相关单元的大小选取不同的代表节点集以满足不同失真度要求。

2.空间相关性模型

2.1 系统模型

本文采用M. C. Vuran等提出事件感知系统模型[8]。描述如下：

(2) N个传感器节点随机均匀地分布在半径为的圆形事件域内，节点静止且位置已知。传感器节点传输半径为Rc，且Rc＜Re，使得事件域内的多个节点要协作完成对事件的感知；

(3) 传感器节点i的坐标为(xi,yi)，其对事件S感知到信息Si的测量值为Xi，Xi是有噪声的，即：Xi=Si+Ni，噪声Ni也是期望为0，均方差为的高斯随机序列，且各个节点的噪声相互独立；

(4) 节点观测到的信息Xi编码为Yi传输给sink节点，sink节点对接收到的M个编码信息 Yi解码后得到Zi，由此获得事件S的估计值这样就可以用失真度衡量估算值的准确性。

由于节点之间相关性的存在，通过M个对事件源进行估算，基于MMSE(Minimum Mean Square Error)原则其失真度可由式(1)计算得到：

其中：

式(2)和(3)分别表示传感器节点之间以及传感器节点和事件源的相关系数。

2.2 环状相关性模型

相关系数的计算主要有四种形式，根据监测事件的物理属性可以选取相关的模型。本文采用能量指数模型，如公式(4)所示，其中

其中相关系数 是和节点之间距离 、节点和事件源距离 相关的，介于[0，1]之间的单调递减非负函数。

当突发事件产生时，一方面，事件域内感知到事件的节点的观测值和事件源的相关度将随着与事件源的距离增加而降低；另一方面，和事件源距离相同的那些节点的观测值，之间相关度较高。因此给出如图1所示的环状相关性模型。图中，事件源位于(0,0)，事件域为半径是500的圆形区域。将节点划分到以事件源为圆心的各个同心圆环中，同一层圆环中节点感知的数据相关性较高。基于此，本文提出NSS算法选取部分代表节点参与数据传输，而普通节点则不传输数据，以此降低能耗。

图1 环状相关性模型示意图

3.NSS算法

为解决事件驱动的传感器网络中选取有效的代表节点集传递感知数据的问题，根据上述环状相关性模型，可以将公式(4)代入式(1)整理后得到：

由式(5)可知，失真度大小与选取的节点个数及其位置相关。为降低失真度，代表节点集 中各节点应满足以下条件：

即在满足最大失真度的要求下选取和事件高度相关，而彼此之间相关性尽可能低的节点集作为代表节点参与信息的传输，事件域中其他节点不参与信息传递，以降低能耗。

因此，本文提出NSS算法：首先将事件域根据环状相关性分层，而后划分相关单元，使得相关单元内的节点相关度较高，最后根据节点支持度得到相关单元的代表节点。NSS算法得到的相关单元为如图1所示的区域。

3.1 事件域分层

根据环状相关性模型，首先应对事件域进行分层，将事件域划分为 个同心圆环，根据和事件源的距离由近及远划分成半径序列为{R1,R2,…,Rk,…,RL}的同心圆环，各层次半径之间的关系如式(8)所示：

其中，k=1,2…,L 表示将事件域划分为L层。R0=0为事件源所在位置；wk为圆环的宽度，最内层的w1可以取值为节点传输半径，因为距离事件一跳范围内的节点相关性较高。wk满足其中圆环相关半径系数1α＜=，表示从事件源由内而外圆环宽度逐步减少或者相等，这是因为根据能量衰减模型，随着距离的增加信号强度下降越快，即随着节点和事件距离的增加，节点之间相关性会逐步减少。

3.2 划分相关单元

根据和事件源的距离确定节点所在层次后，本文将各个圆环区域进一步划分成一个个面积相同的相关单元，相关单元内的节点对事件源的感知信息相似。其如图2中阴影显示的是半径分别为1kR-，的相邻两层同心圆环中的两个相关单元。

若和事件源S最近的第一层初始圆心角为β1，以事件源S为圆心，各层中相关单元的圆心角βk（k=1,2,…,L ）可以用式(9)依次求得：

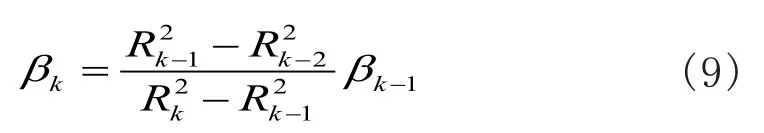
考虑到空间相关和节点间距离关系密切，可以认为相关单元内的节点之间具有最大的相关度，只要选择其中一个作为代表节点即可。显然，1β越大，相关单元的面积越大。

图2 相关单元示意图

3.3 确定代表节点

考虑公式(6)和(7)的约束，选择距离事件源较近而彼此之间较远的节点能有效地降低失真度。为评价节点和本层其他节点的接近程度，本文引入节点支持度（Node Supported），定义如下：

其中j=1,2…,n为节点i所在层的其他节点个数。Ci越小，说明节点 和其他节点感知的数据越接近，其他节点和节点i的相关性越高，节点i具有代表性。

综上，NSS算法流程如下：

1 输入:S //事件源发生位置(xe,ye)，事件半径 Re

α，β1，Rc//圆环相关半径系数、相关域初始角度和节点感知半径

Φ(N) //感知到事件的N个节点集，节点i的位置(xi,yi)

Dmax//最大失真度

2输出:Φ(M) //代表节点集

3R0=0，计算Rk=Rk-1+wk，其中k=1,2…,L

4β1=π,根据计算各层圆心角度数

5 for each ∈()NΦ

计算,sid //计算节点和事件发生位置的距离

if,sid＞=kR and,sid＜1kR+

得到节点i所属层次编号为1kL+

end

根据所属层次的1kβ+，得到节点i所属的相关单元

end

61l=，()DM=0

7forl层的各个相关单元

end

8 根据式(5)计算失真度()DM

9 ifD(M)＞Dmax且l≤L

l=l+1

转7，继续选择代表节点

end

10 输出代表节点集()MΦ及()DM

NSS算法基于相关性将事件域划分为若干相关单元，各个相关单元依据节点之间的支持度选取具有代表性的部分节点参与数据的传输，能有效降低无线传感器网络总的数据传输量，从而有效降低能耗。公式(5)显示失真度的大小和参与运算的节点个数M、节点和事件源的距离及节点之间的距离相关，而NSS算法中可以通过调整圆环相关参数以得到不同的代表节点个数满足实际应用的需求。

4.性能分析及仿真

下面就本文提出的NSS算法用Matlab进行仿真，仿真参数见表1所示。4.1分析算法中各个参数对算法性能的影响，结果表明通过调整相应参数可以得到不同的代表节点集以满足不同的应用场景；4.2在同等条件下比较相关算法对事件估计的失真度以及选取的代表节点个数占总节点数比例，仿真显示NSS只需要选取较少的代表节点就能得到对事件源较为理想的估算精度。文中所有数据都是1000次试验的平均值。

4.1 NSS算法性能分析

NSS算法中代表节点个数和相关单元的个数息息相关，而这又依赖于网络中的参数。

表1 仿真参数

节点感知半径Rc的影响：图3显示β1=π，Rc分别为{50，100，150，200}时，代表节点的个数以及失真度变化曲线。图中显示：随着感知半径cR的增大，代表节点个数减少，失真度也有所增加。这是因为当cR变大即节点感知的范围增大，使得相邻节点覆盖重叠范围也增加，感知信息大量冗余，这时只需要较少的代表节点。仿真也显示，虽然cR取值不同，但是当代表节点数接近10左右时失真度最小，此后增加代表节点个数，失真度不但没有降低反而有所增加，分析后知道，随着远离事件源的节点的加入，外界的干扰逐步增大，失真度会略微增加，这也是算法中考虑到感知节点和事件源位置的结果。

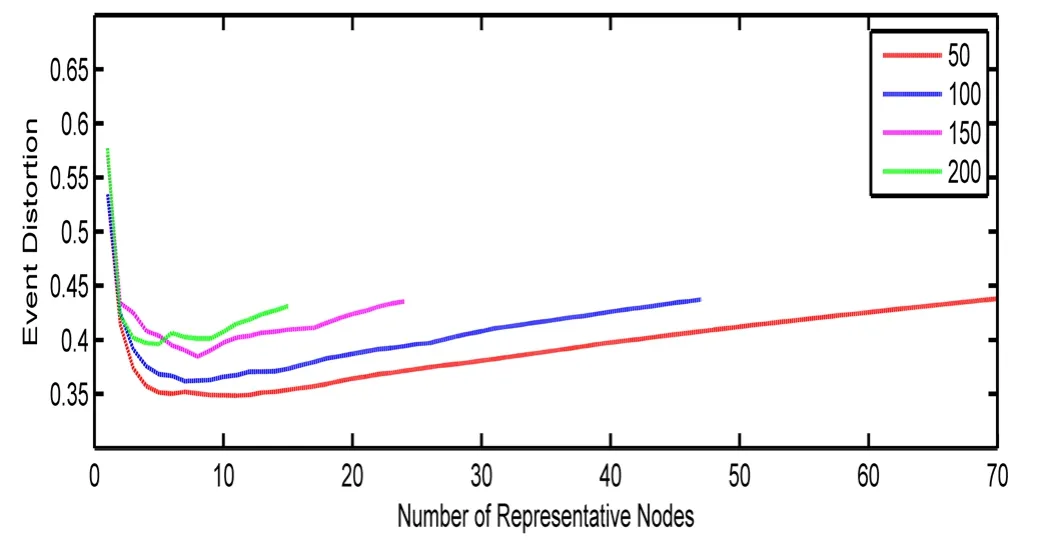
图3 感知半径对算法的影响

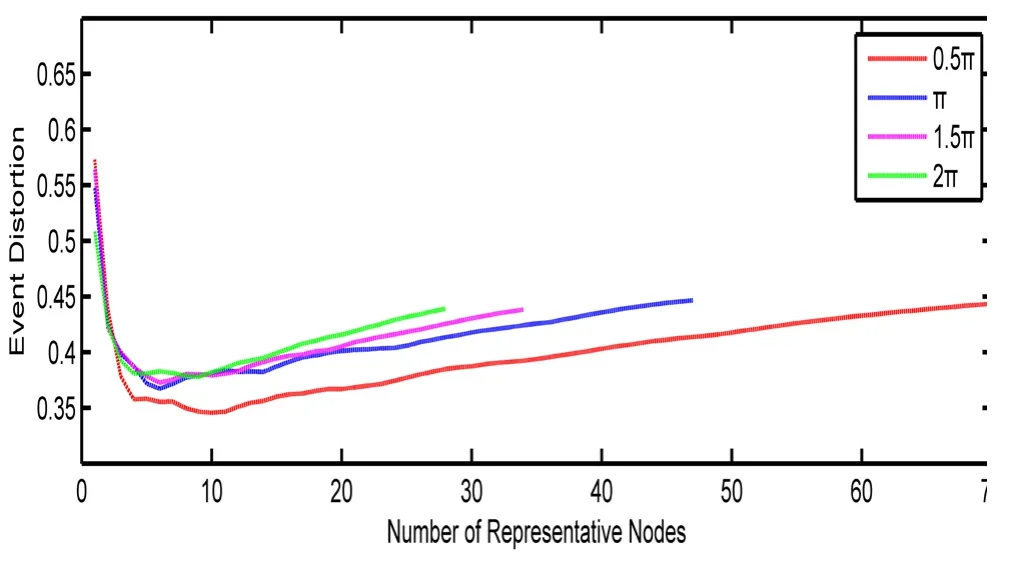
图4 初始角对算法的影响

初始角度1β的影响：图4显示cR=100，1β分别为0.5π，π，1.5π，2π时代表节点的个数以及失真度曲线。图中显示，随着1β的增加，代表节点个数减少，失真度却增大了。这是因为初始角度增加，相关单元的面积增大，划分的相关域个数减少，代表节点相应减少。但是相关单元面积增大后，节点之间感知数据的相关度减少，因此失真度变大。但是，不管选取怎样的1β，失真度变化的趋势是一致的。

图5 节点个数对算法的影响

节点数N的影响：图5显示cR=100，1β=π，事件域内N的个数分别为50、100、300、1000的情况，结果显示：随着事件域内感知的节点数量增加，失真度会变小，这是因为同样的事件域内感知到的节点个数越多，节点之间的相关度越高，感知的信息也越准确。值得注意的是，本文提出的NSS算法不仅能迅速找到具有代表性的节点，使得失真度快速下降，而且代表节点集的个数并没有随着节点个数的增加而迅速增加。这说明节点规模增加对算法影响不大。

图6 算法性能比较

4.2 相关算法比较

为了评估算法的效果，在半径为500的事件域中部署的节点数N分别为{50，80，100，150，200，250，300，350，400，450，500，600，700，800，900，1000}，计算最小失真度和选择的代表节点数M占总节点数N的百分比，以此比较本文提出的NSS算法以及文献[8]中提出的随机节点选取和其后的INS算法的性能。仿真结果如图6所示，图中显示，在同样的环境下，随机选取节点的算法波动性比较大，这是因为选择的节点的位置是随机的，造成对事件的感知精度也不确定。INS算法中代表节点选取节点总数的20％～40％能得到较小的失真度。而NSS算法能得到更为理想的失真度，代表节点数占总节点数的比例在N较小时较高，但是随着N的增加迅速下降，逐渐趋于稳定。分析后知道，算法中优先考虑距离事件源较近的节点，能较好地反映事件真实信息，有利于降低失真度。但是当事件域内节点数目较少时，节点之间的相关度不高，相对需要较多的代表节点参与信息的感知，之后随着节点的逐步增加，节点感知信息之间的冗余增加，所选的代表节点个数占总节点数的比例逐步下降。

5.结论

针对事件驱动传感器网络中如何选取代表节点集传递感知数据来以获取满足一定精度要求的事件信息的问题，本文利用节点之间的空间相关性，在环状相关性模型基础上提出NSS算法，将事件域划分为若干相关单元，并选取合适的节点作为代表节点协作参与数据传输。仿真表明算法性能稳定，且能通过相关参数的调整满足不同精度或应用要求，算法能适应不同规模的无线传感器网络。

6.致谢

本文章服务于国家自然科学基金资助项目（61300239）。

[1] G. Anastasi, M. Conti, M. Francesco. Energy Conservation in Wireless Sensor Networks: A survey. Adhoc Networks, 7:537-568, 2009.

[2] I. F. Akyildiz, W. Su, Y. Sankarasubramaniam, and E. Cayirci. Wireless Sensor Networks: A Survey. Computer Networks, 38:393 422, 2002.

[3] M. Mitici, J. Goseling. Decentralized vs. Centralized Scheduling in Wireless Sensor Networks for Data Fusion. Acoustics, Speech and Signal Processing (ICASSP), 2014.

[4] Eskandari Z. , Yaghmaee M.H. , Mohajerzadeh A.-M. Automata Based Energy Efficient Spanning Tree for Data Aggregation in Wireless Sensor Networks. Communication Systems , ICCS 2008. 943-947,2008.

[5] Kulkarni, R.V. , Venayagamoorthy, G.K. Particle Swarm Optimization in Wireless Sensor Networks: A Brief Survey. Systems, Man, and Cybernetics, Part C: Applications and Reviews, IEEE Transactions on Volume 41, Issue 2: 262- 267, 2011.

[6] Leandro A. Villas, Azzedine Boukerche. An Energy-Aware Spatial Correlation Mechanism to Perform Efficient Data Collection in WSNs. 11th IEEE International Workshop on Wireless Local Networks:882-889,2011.

[7] L. Doherty, K.Pister. Scattered Data Selection for Dense Sensor Networks. In Proceedings of IPSN’04, 2004.

[8] M. C. Vuran and B. Akan, I. F. Akyildiz. Spatiotemporal correlation: theory and applications for wireless sensor networks. Computer Network, vol. 45, no. 3,pp. 245 259, Jun. 2004.

[9] Gedik.B., Ling Liu and P.S. YU. ASAP: An Adaptive Sampling Approach to Data Collection in Sensor Networks. IEEE Transactions on Parallel and Distributed Systems, 18: 1766 1783, 2007.

[10] S.S. Pradhan and K. Ramchandran, Distributed Source Coding Using Syndromes (DISCUS): Design and Construction. Information Theory, IEEE Transactions 49: 626-643, 2003.

[11] Karjee, J. , Jamadagni, H.S. Data Accuracy Estimation for Cluster with Spatially Correlated Data in Wireless Sensor Networks. Communication Systems and Network Technologies (CSNT):427- 434,2012.

[12] Arnoldo Díaz-Ramíreza, Luis A. Tafoyaa, Jorge A. Atempaa, and Pedro Mejía-Alvarezb. Wireless Sensor Networks and Fusion Information Methods for Forest Fire Detection. Procedia echnology 3:69 79, 2012.

[13] Singh P. , Kumar R. , Kumar V.. An Energy Efficient Grid based Data Dissemination Routing Mechanism to mobile sinks in Wireless Sensor Network. Issues and Challenges in Intelligent Computing Techniques (ICICT): 401-409, 2014.

[14] Mehmet C. Vuran, and Ian F. Akyildiz. Spatial Correlation-based Collaborative Medium Access Control in Wireless Sensor Networks. IEEE/ACM Transactions on Networking. 14: 316 -329, 2006.

[15] Zoghi, M.R. ; Kahaei, M.H. Efficient sensor selection based on spatial correlation in wireless sensor networks. Computer Conference: 627- 632,2009.

[16] 苏威,林亚平,尤志强,胡玉鹏,周四望. 无线传感器网络中一种环状空间相关性模型. 计算机应用研究,2008(25):1860～1863

[17] Ren Guocan, Ding Guowei. An Improved Isoline based Data Aggregation Scheme in Wireless Sensor Networks . Procedia Engineering,23: 326 332,2011.

An Efficient Node Selection Method in Event-Driven Wireless Sensor Networks

Zhu Min-ru, Guo Jian
(College of Computer, Nanjing University of Posts and Telecommunications, Jiang su Province, Nanjing 210003, China)

Event-driven wireless sensor networks need to make reasonable judgments for event states. In this paper, we study how to select a small number of active nodes so as to reduce energy consumption and acquire event states with minor cost. The proposed NSS (Node Supported Selection) algorithm exploits the spatial correlation in nodes and makes use of node supported degree to select representative nodes involved in data transmissions. Simulation results show that this algorithm can keep data accuracy with a small ratio of nodes. Besides, the performance of NSS is better than other algorithms, especially, it has good scalability.

Wireless Sensor Networks; Circular Spatial Correlation Model; Efficient Node Selection; Distortion

TP212

A

1009-5624-（2016）02-0051-06