对一个数学模型的思考
——从2016年淄博市中考第24题说起
2016-02-07山东省淄博市周村区城北中学
山东省淄博市周村区城北中学
张 俊 (邮编:611731)
对一个数学模型的思考
——从2016年淄博市中考第24题说起
山东省淄博市周村区城北中学
张 俊 (邮编:611731)
笔者近来对2016年淄博市中考第24题进行研究,发现该题题目典型,思路开阔,平面几何知识交叉丰富,可拓展,可延伸,本文结合该题对相关的命题导向和教学导向,与大家研讨.
1 题目呈现
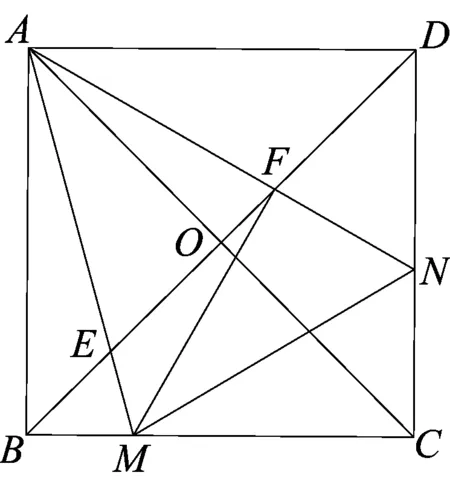
图1
(2016年淄博中考第24题)如图1,正方形ABCD的对角线相交于点O,点M、N分别是边BC、CD上的动点(不与点B、C、D重合),AM、AN分别交BD于点E、F,且∠MAN始终保持45°不变.
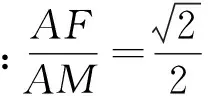
(2)求证:AF⊥FM;
(3)请探索:在∠MAN的旋转过程中,当∠BAM等于多少度时,∠FMN=∠BAM?写出你的探索结论,并加以证明.

图2
2 思路突破
1.1 识别相似模型,问题迎刃而解

图3
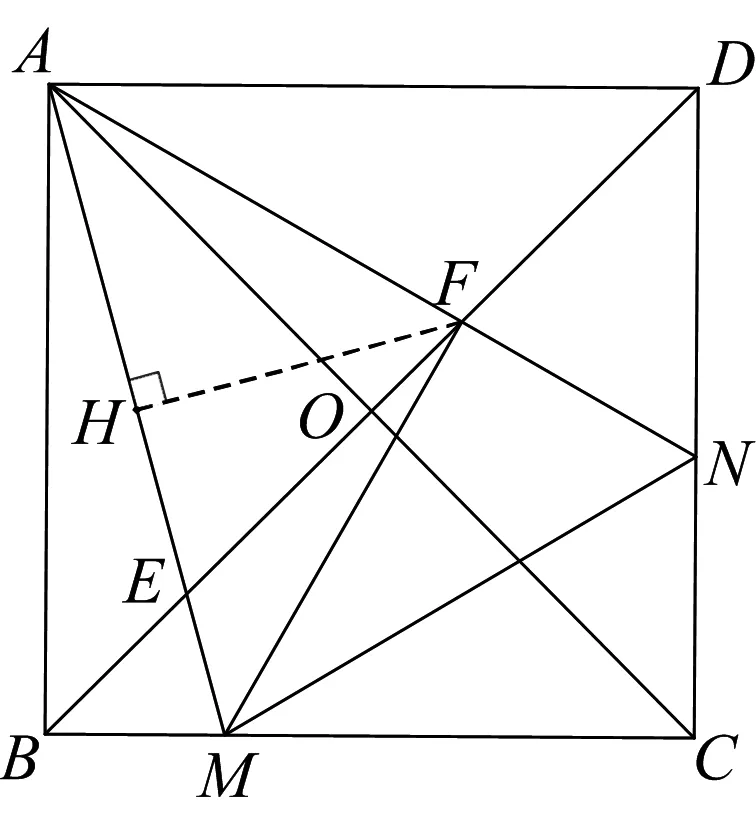
图4

1.2 利用已证结论,进而递进求解

3 巧用“8”字型,得出关键角
第3问看到网上很多答案是利用点A、B、M、F四点共圆来解答,尽管思路简洁,但考虑四点共圆新的课程标准已经不做要求,学生也较难想到,那么我们还有更自然和常规的方法吗?如图5,我们可以从复杂图形中抽取出这对“8”字型,因为∠ABF=∠AMF=45°,又∠AEB=∠MEF, 所以∠BAM=∠MFB.当∠FMN=∠BAM时,得∠FMN=∠MFB.所以BF∥MN,即∠DBC=∠NMC=45°,△NMC为等腰直角三角形, 所以CM=CN,进而BM=DN,易得△ADN≌△ABM,因为∠MAN=45°,则∠BAM=∠DAN=22.5°,即∠BAM=22.5°时,∠FMN=∠BAM.

图5

图6

图7

图8

图9
4 模型思考
通过以上问题解决我们可以感受到本题是以熟悉的半角模型为背景进行的一次命题考查,这不禁使笔者想到了半角模型的一个典型问题:如图6,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,求证:EF=BE+DF.
评析 该问题常规的思路可以用截长补短法,如果我们从图形变化的角度来思考会更有数学的味道,思路简述1:如图7,把△ABE绕点A逆时针旋转90°,易证△AEF≌△AGF,进而求证.思路简述2:如图8,把△ADF沿AF对折,连接ED′,可证△ABE≌△AED′,进而得到点E、D′、F共线,进而求证.以上给我们提供了解决半角模型的常用方法和思路.
如果我们再连接对角线BD,交AE、AF于点M、N,如图9,求证: MN2=BM2+DN2.

图10
思路简述 如图10,把△ABM绕点A逆时针旋转90°到△ADM′,连接NM′,易证△ANM≌△ANM′,因为△NM′D为直角三角形,利用勾股定理进而求出关系,这里也可以选择轴对称思路来分析,不再赘述.
如果我们再把上述图形抽象化,就可建立下面的基本模型:如图11,等腰直角三角形ABC中,∠BAC= 90°,AB=AC,点M、N在边BC上,且∠MAN= 45°,求BM、MN、NC之间的数量关系.

图11
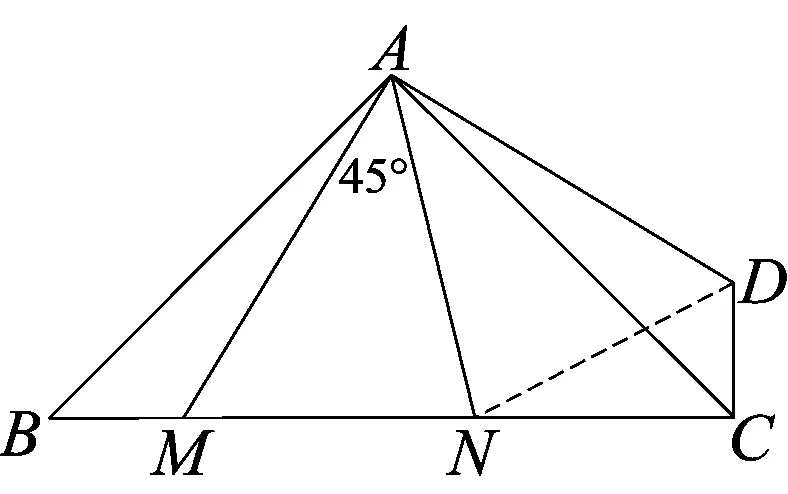
图12
评析 如图12,我们依然把△ABM把绕点A逆时针旋转90°得到△ACD,可以证得△AMN≌△ADN,把线段BM、MN、NC,转化到了△DCN中,由于∠DCN=∠ACD+∠ACB=45°+45° =90°,所以根据勾股定理可得DN2=CD2+CN2,即MN2=BM2+NC2.这样我们就得到了半角模型的一个基本结论, 2014年浙江绍兴中考试题的23题,2016年广西贵港的26题都以此进行了命题考查.

图13
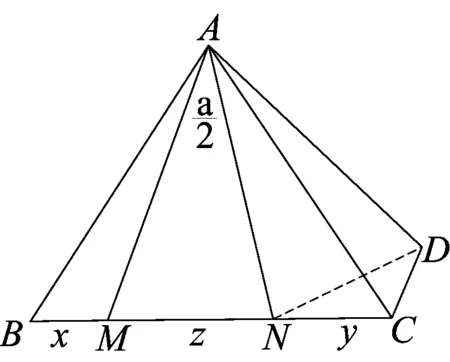
图14

在这里我们依然可以采用旋转变化的方式,如图14,把线段x、y、z转化到△DCN中,利用三角函数可得到一般化的结论:z2=x2+y2+2xycosα (有兴趣的老师可以证一下,这里不再赘述),从而,对于α=90°其实就是半角模型的一种特殊情况,这也是问题的本质所在.
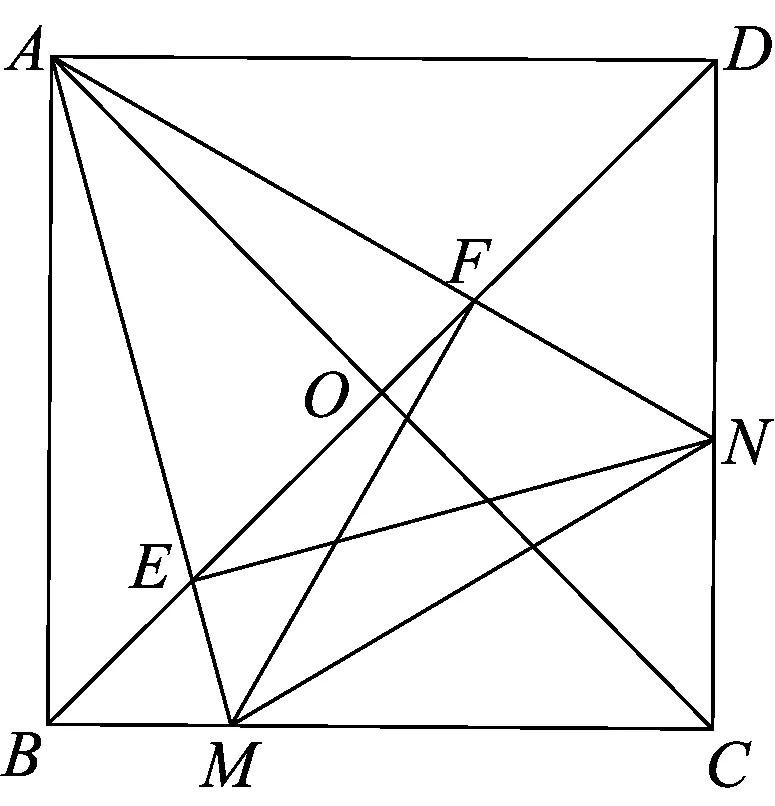
图15
从2016年淄博市中考第24题,我们可以看到,以半角模型为载体的中考命题这几年一直活跃在各地市的中考试卷中.原因在于该模型能把众多的平面几何知识融合在一起,结论比较开放,变式较多,给命题者留下了广阔的思考空间.基于本题的半角模型,我们继续挖掘还可得出以下结论:如图15.
(1)∠AMB=∠AMN=∠AFB或∠AND=∠ANM=∠AED;
(2)2AE2=BE2+DE2或2AF2=BF2+DF2;
(3)△AFM与△AEN都是等腰直角三角形;

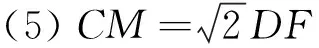
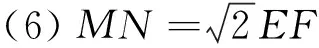
同时,我们还可继续发现,2016年淄博市中考24题中的第2问中,如果我们把∠MAN=45°绕点A继续旋转,如图16,可以得到△AFM始终是等腰直角三角形,揭示了变化中的不变.
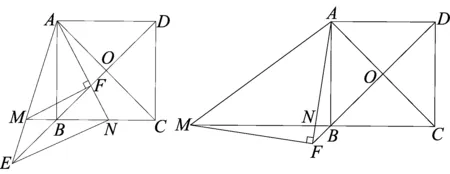
图16
5 教学导向
4.1 基于模型,寻求模型本质
《数学课程标准》在几何方面的学习要求是让学生“能从较复杂的图形中分解出基本的图形,并能分析其中的基本元素及其关系,利用直观来进行思考”.因此,这就要求我们教师在教学中要不断引导学生将同种类型的问题进行合理归纳、梳理,进而形成一个几何模型.例如本文所探讨的半角模型,在数学学习中,我们提倡追根溯源,寻找问题之间的相互联系,从而对问题的研究形成系统性,同样在几何模型教学时,要让学生循序渐进,找到模型的变化和迁移,从而对一类问题找到本质特点.例如淄博市中考第24题的第1问不仅要得出相似,而且要引导学生从图形变化的角度理解到其实是有一个三角形按照一定的比例放大或缩小,绕一个顶点旋转得到的,让学生从旋转相似的本质来理解,同样对于前面z2=x2+y2+2xycosα的探究,让学生经历特殊到一般的理解过程,不仅知其然,更要知其所以然,进而积累出解决这类问题的方法和思路.
4.2 基于模型,开展变式教学
就半角模型而言,通过改变不同的条件,我们可以得出不同的结论,正是由于其典型,因而大有文章可做,在实际的教学中,我们要抓住平时教学中具有代表性的数学模型,发挥学生的主动性开展变式教学,让学生对问题进行不同角度、不同层次、不同情形、不同背景的变式,通过变式达到一题多用,多题重组,可以促使学生的思维向多维发散.
1 刘文燕. 数形结合明结构,以退为进获思路[J]. 中学数学(下),2015(8)
2 中华人民共和国教育部制订.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012
2016-09-27)
