机器人机构设计的运动灵活性评价方法*

应明峰，莫晓晖，姜 劲

(金陵科技学院 a.机电工程学院；b.计算机工程学院，南京 211169)

机器人机构设计的运动灵活性评价方法*

应明峰a，莫晓晖b，姜 劲a

(金陵科技学院 a.机电工程学院；b.计算机工程学院，南京 211169)

以一种工业机器人为研究对象，在机器人运动学的基础上，分析其全域运动性能平均指标、全域运动性能波动指标、全域运动性能最差指标，并针对这3项性能指标进行多目标优化。将机器人杆长参数作为机构设计变量，根据机器人的工作空间及运动学灵活性要求建立多目标优化模型。设计一种改进的多目标粒子群算法，引入Pareto分布熵及其差熵估计种群的多样性及进化状态，以此为反馈信息来设计进化策略。进行优化计算，最终得到一组最优解。采用优化后的机器人机构参数可以使机器人运动灵活性能有较大提高。

机器人运动学；性能指标；Pareto 熵；多目标粒子群优化

0 引言

机器人机构设计是一个困难而复杂的问题，往往需要依赖性能指标来评价机器人机构设计的好坏，因此在设计过程中不可避免地要考虑选取合适的性能评价指标[1]。在机器人性能指标的研究上，国内外许多学者做了大量的研究工作，并取得了许多成果。YOSHIKAWA[2]定义了机器人的可操作度，并利用可操作度椭球对其几何意义进行了阐述。SALISBURY等[3]提出了条件数，并将其用于机器手指的工作空间进行评价。

但是由于雅可比矩阵依赖于机器人具体的位姿，因此基于雅可矩阵的条件数指标、可操作度指标都只是一个局部指标，它们的优化往往具有局限性。如果能够对机器人运动学多个性能评价指标之间进行耦合及制约问题加以研究，进而将其运动学性能进行多目标优化，这对所设计的机器人机构性能的评价具有重要意义。一些学者已经在机构多指标优化评价问题上做了相关研究工作。Zhang Lufan[4]采用改进的多目标遗传算法优化了宏微观运动平台连接机构的总质量、关键点最小变形以及第1阶固有频率。Zhang Dan[5]引入了粒子群优化算法对土拨鼠机器人的刚度和工作空间进行了优化。

粒子群算法使近年发展起来的一种新的进化算法，具有形式简洁、收敛快速和参数调节机制灵活等优点，并且一次运行可得到多个解，因而被认为是求解多目标优化问题最具潜力的方法之一。本文采用改进的多目标粒子群优化方法进行一种焊接机器人机构设计的运动学性能多目标优化与评价。通过对机器人的机构分析，建立其运动学性能的多目标优化模型。以机器人运动灵活性能指标条件数的全域运动平均性能、全域运动波动性能、全域运动最差性能3个指标为优化目标，以机器人的机构杆长参数为优化变量进行多目标优化，比较机构杆长参数的变化对机器人运动灵活性能的影响，最后获得较好的机构设计参数值。

1 机器人性能优化问题描述

1.1 机器人模型的建立

图1为六自由度焊接机器人模型示意图，由6个转动副构成，该机器人是一种典型的串联机器人。由于它的灵活性，可以广泛应用于弧焊、涂胶、切割、喷漆等多种领域。

图1 机器人结构简图

按照D-H标准建立坐标系，可得出该机器人的D-H 参数见表1。

表1 机器人的D-H连杆参数

为了分析机器人的运动学，根据机构影响系数法[6]建立一阶影响系数矩阵。Si表示连杆i轴线方向的单位矢量，Ri表示坐标系i与固定坐标系两原点之间的距离，(P-Ri)表示连杆i对研究点P的矢径，则机器人一阶影响系数雅可比矩阵J为：

(1)

1.2 优化指标

雅可比矩阵的条件数[3]代表了雅可比转换矩阵向各个方向的变化均一性，在机器人机构设计和对机器人进行控制时，需使雅可比矩阵尽量各向同性，即尽量“均匀”，就是要控制雅可比矩阵的条件数尽量接近1。但是该指标只是用于表示机器人的局部的一个性能值，并不能反映机器人在工作空间的整体性能指标，为此Gosselin等定义了一个新指标η[7]：

(2)

η是一个全域性能指标，它等于机器人工作空间w内所有观测点的局部指标条件数k倒数的平均值。为了考虑到机器人在工作空间内性能指标的变化，石志新等[8]在η的基础上又提出了全域性能波动指标σ：

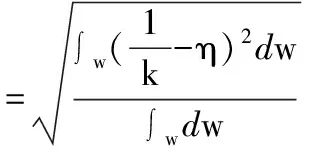
(3)

η和σ两个指标是对机器人整个工作空间内的灵活性进行评价，可用于机器人机构设计中工作空间综合问题的求解，以及在机器人工作过程中，机器人与工件对象之间的相对最优位姿求解。

以上两个指标都可以对机器人运动灵活性进行量化描述，从而给机器人机构的优化设计提供了重要的评价准则。但是由于实际工程问题的复杂性和多样性，这些灵活性指标之间是相互关联影响的。除了考虑机器人运动性能的要求以外，还要强调其综合运动灵活性能的优劣。特别是对于一个具体任务构成的空间，使机器人以一定位姿处于工作空间内的某一位置时，如果想知道机器人对于这个具体任务能否完成，或者完成时执行质量如何，除了考察在此任务空间上机器人运动灵活性的整体情况以外，还需要考虑最差情况。因为在最差情况下机器人如果不能完成任务或完成的质量差，都会影响整个任务完成质量，仅凭η和σ两个指标来衡量时，只能知道工作空间中运动灵活性总体状况和波动情况，因此考虑增加一个描述最差灵活性情况的指标δ：

δ=η-kmin

(4)

它由表示整体灵活性的指标η与观测点中条件数最小值kmin的差来评价，δ越小，说明在任务空间上灵活性变化幅度越小。

1.3 数学描述

研究的目的是在考虑机器人的设计要求基础上，找到最优的机构杆长，使该机器人工作时发挥最优的运动性能。在设计要求的基础上综合考虑机器人运动学性能的变化，将需优化的变量机构杆长进行条件约束，以确保机器人整体尺寸在一定范围内变化，不超出设计要求。

采用目标函数的最小方向寻优，对三个指标η、σ与δ进行变化后分别建立目标函数f1、f2、f3进行多目标优化，最终找到机构杆长l1和l2一些最优的组合。

该优化问题的数学表示如下：

minf1(l1,l2)

minf2(l1,l2)

minf3(l1,l2)

(5)

s.t.100mm≤l1≤700mm

100mm≤l2≤400mm

(6)

2 工程实例分析

2.1 优化算法

很多工程问题都可以归结为多目标优化问题，其求解方法一直都是学术界和工程界共同关注的焦点。多目标优化问题通常存在多个彼此冲突的目标，其优化结果为Pareto 最优解集[9]。与数学规划方法相比，进化算法因一次运行可得到多个解，且能逼近非凸或不连续的Pareto 最优前端，从而被认为是更适合求解多目标优化问题的智能方法。

粒子群优化算法(particle swarm optimization,简称PSO)[10]是由Kennedy和Eberhart在1995年提出的仿生算法，它是受到飞鸟集群活动规律的启发，根据社会学和心理学而建立的群体智能模型。

熵在热力学中表示系统混乱状态[11]，而在生态学中表示生物的多样性，它可以来度量近似Pareto前端的分布均匀性，从而体现出进化算法中种群的多样特性。具体可以通过对目标空间变换来获得Pareto前端的熵，先对优化算法中种群的多样性进行度量，对于Pareto前端在相邻迭代时刻的熵的变化大小，用差熵来表示，以此来估计种群的进化状态，从而得到实时的进化环境反馈信息。同时，在变换后的目标空间中为了评估Pareto最优解，使其能够逼近真实的Pareto综合程度，采用了个体格距离密度和格占优强度为算法中外部档案更新和全局最优解选择提供决策依据。

为了解决机器人机构设计中的性能优化问题，采用了一种基于Pareto熵的多目标粒子群优化算法，流程图如图2所示。

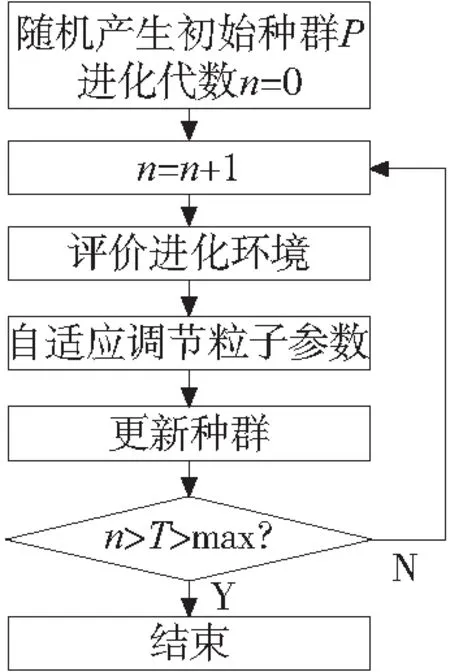
图2 算法流程图

其算法流程如下：

输入：具有M个目标的待优化问题MOP，具有D个决策变量的搜索空间SD；

初始化参数：最大外部档案容量F，种群粒子个数PN，最大迭代次数T_max；

输出：存储在外部档案中的近似Pareto最优解集G_pa。

步骤1：初始化：产生初始化种群P，令迭代计数器n=0，在搜索空间SD中按均匀分布随机生成PN个粒子，计算每个粒子的M个目标函数值，初始化每个粒子的外部档案Pa，更新G_pa；

步骤2：更新迭代的计数器：t=t+1；

步骤3：评估其进化的环境：计算G_pa的Pareto熵和差熵，评估种群进化状态Status，计算G_pa中每个Pareto最优解的个体格距离密度和个体格占优强度；

步骤4：自适应调节粒子运动参数,计算当前粒子运动参数；

步骤5：更新种群：选择粒子i的全局最优解

gBest(i),从Pa(i) 中选择一个与gBest(i)空间距离最近的成员作为粒子i的个体最优解pBest(i)，更新粒子i的速度和位置，评估粒子i的M个目标函数值，更新粒子i的个体外部档案Pa(i)，更新全局外部档案G_pa；

步骤6：检测算法终止条件：如果n>T_max，则输出G_pa;否则，跳转步骤(2)。

2.2 优化结果及分析

根据焊接机器人的工作空间及运动学性能要求，设定机器人初始机构杆长l1=200mm，l2=150mm，将表1中其他连杆参数取值a1=260mm,a3=35mm，d1=675mm,d6=115mm。此时，计算所得的机器人3个优化目标函数值分别为：f1=56.8532，f2=80.2851，f3=233.2060。

接着根据输入变量、优化的目标以及约束条件，编写MATLAB优化函数，设定粒子群算法参数，种群大小设为N=500，最大外部档案容量F=500，最大迭代次数T_max=400。算法运行后得到优化结果，以l1作为x轴，l2作为y轴，绘制出各个性能指标随l1、l2变化的等高线分布图3。

(a)指标1等高线分布图

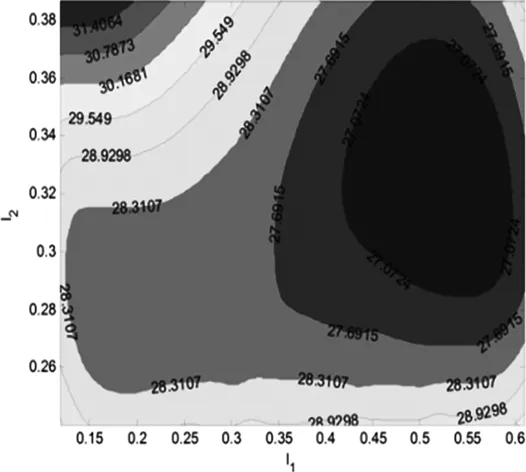
(b)指标2等高线分布图

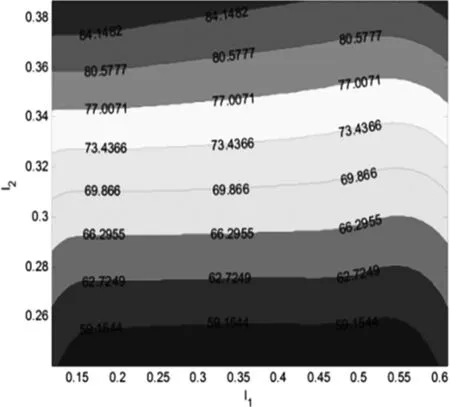
(c)指标3等高线分布图图3 三个优化指标的等高线分布图

由图3中可以看出，三个指标随着机器人机构杆长的优劣变化趋势是不同的，如果仅仅追求某一个性能指标的最优，可能会影响到其他指标的性能，因此只能找寻一些具有较好综合性能的杆长组合。根据Pareto效率从最后优化的解集中取10组Pareto最优解，如表2所示。

表2 机构参数优化结果

将优化的结果与初始数值进行比较，做出散点图，如图4所示。

(a)全域性能均值比较图

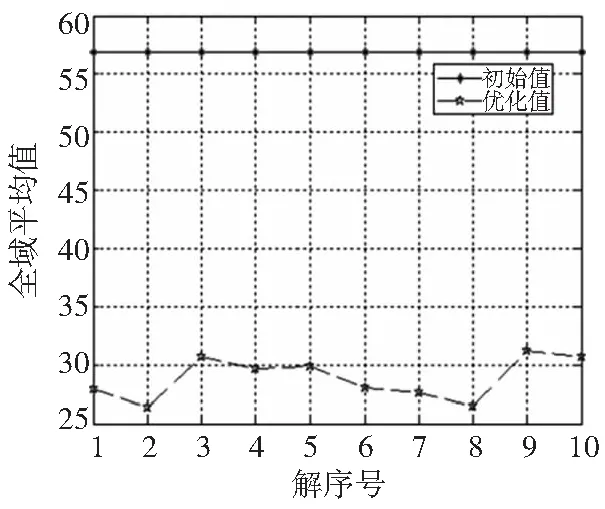
(b)全域性能波动值比较图

(c)全域性能最差值比较图图4 优化结果对比图

经过比较可以发现，优化计算后获得的10组解可以使机器人运动性能指标条件数的全域性能平均值优化45.10%～53.57%，全域性能波动值优化61.51%～65.46%，全域性能最差值优化64.23%～75.70%。比较分析后，最终选择l1=440.2mm，l2=299.1mm作为机构杆长值。采用此种组合机构构型的机器人性能指标条件数的全域运动性能平均值可以优化 50.68%，全域运动性能波动值优化65.32%，全域运动性能最差值优化71.05%。算法的运算时间约300s，运算效率有很大提高。

3 结论

通过对一种串联机器人进行机构设计的运动学性能评价分析，得到了机器人性能的多目标优化模型。将机器人运动灵活性指标条件数的全域平均性能指标、全域波动性能指标、全域最差灵活性指标作为三个优化目标。利用多目标粒子群算法，引入Pareto效率对它们进行优化。将优化后的Pareto第一前端最优解集进行数据分析，最终经优化计算得到了较好的机构杆长参数组合，实现了机器人的机构优化，使机器人运动灵活性能有了较大提高。

[1] 邹慧君，高峰．现代机构学进展[M]．北京:高等教育出版社，2011.

[2] YOSHIKAWA T. Manipulability of robotic mechanisms[J]. International Journal of Robotics Research，1985，4(2)：3-9.

[3] SHH Zargarbashi, W Khan, J Angeles. TheJacobian condition number as a dexterity index in 6R machining robots[J]. Robotics and Computer-Integrated Manufacturing，2012, 28(6):694-699.

[4] Zhang Lufan, Long Zhili, et al. Multi-objective optimization design of a connection frame in macro-micro motion platform[J]．Applied Soft Computing，2015，32: 369-382.

[5] Zhang Dan, Gao Zhen. Forward kinematics analysis and multi-objective optimization of a bio-inspired parallel manipulator[J]．Robotics and Computer-Integrated Manufacturing，2012，28(4): 484-492.

[6] 于靖军，刘辛军，丁希仑，等．机器人机构学的数学基础[M]．北京: 机械工业出版社，2008.

[7] Gosselin C, Angeles J. A Global Performance Index for the Kinematic Optimization of Robotic Manipulators[J]. Transaction of the ASME, 1991, 113(3):220-226.

[8] 石志新，罗玉峰，陈红亮,等．机器人机构的全域性能指标研究[J]．机器人，2005，27(5)：420-422 .

(Shi Zhi-xin, Luo Yu-feng, Chen Hong-liang,et al. On Global Performance Indices of Robotic Mechanisms[J]. Robot, 2005,27(5):420-424.

[9] H Safikhani, S Eiamsa-Ard. Pareto based multi-objective optimization of turbulent heat transfer flow in helically corrugated tubes[J]. Applied Thermal Engineering, 2016, 95:275-280.

[10] H Zhang, DD Kennedy, et al. Novel bare-bones particle swarm optimization and its performance for modeling vapor-liquid equilibrium data[J]. Fluid Phase Equilibria, 2011,301(1):33-45.

[11] SA Matei, RJ Bruno. Pareto's 80/20 law and social differentiation:A social entropy perspective[J]. Public Relations Review, 2014,41(2):178-186.

(编辑 李秀敏)

Assessment of Kinematic Flexibility on Robotic Mechanism Design

YING Ming-fenga，MO Xiao-huib，JIANG Jina

(a.School of Electrical Engineering;b. School of Computer Science and Technology, Jinling Institute of Technology, Nanjing 210016, China)

Based on the kinematics of an industrial robot, the three indices, including global kinematic average value, global kinematic volatility, global kinematic worst value are analyzed and optimized by multi-objective optimization algorithm. The link length parameters of robot are design as the variable, and the multi-objective optimization model is established by the requirements of the robot workspace and kinematics. An improved multi-objective particle swarm optimization (pso) algorithm is designed by using the distribution entropy and its difference of an approximate Pareto front to assess the diversity and evolutionary status of the population, and getting feedback information to design evolution strategy. Finally, a group of optimum link length is calculated by using this method. The optimized link length parameters of robot can improve the performance index of the robot greatly.

robot kinematics; performance index; Pareto entropy; multi-objective particle swarm optimization

1001-2265(2016)12-0157-04

10.13462/j.cnki.mmtamt.2016.12.042

2016-02-23

江苏省高校自然科学基金(14KJD510003)；国家自然科学基金(61540068)

应明峰(1979—)，男，南京人，金陵科技学院副教授，研究方向为机器人运动控制与优化，(E-mail)ymf990@jit.edu.cn。

TH166;TG659

A