虚拟制造单元瓶颈缓冲区容量优化*

吕 洁， 郭婷芳, 韩文民

(江苏科技大学 经济管理学院，江苏 镇江 212000)

虚拟制造单元瓶颈缓冲区容量优化*

吕 洁， 郭婷芳, 韩文民

(江苏科技大学 经济管理学院，江苏 镇江 212000)

文章是在虚拟制造单元的生产方式下，基于约束理论考虑面向多个加工任务同时进行加工时瓶颈资源问题，以减少生产波动对瓶颈资源的影响来针对缓冲区容量问题进行研究，以最优缓冲区容量为目标建立目标函数模型，利用改进遗传算法求解，同时结合在制品拒绝率、在制品数量和设备的利用率等指标来评价缓冲区容量的优劣。最后，通过某船厂的实际数据进行验证，运用MATLAB进行仿真，仿真结果验证了方法的有效性和可行性。

虚拟制造单元；瓶颈资源；缓冲区容量；遗传算法

0 引言

虚拟制造单元(本文简称为虚拟单元)是指设备在物理位置上不改变，逻辑上对生产资源进行动态配置和重组[1]，且因其设备调整时间高效性和灵活性，加快了对市场的响应速度[2]。基于约束理论基础可知，瓶颈资源的利用程度会导致资源间的冲突，从而直接影响整个系统的生产能力和效率，所以，只有合理的设置瓶颈资源的相关参数，才能提高系统的生产率[3-4]。资源之间的冲突问题可通过设置缓冲区来协调，并结合符合生产实际的调度策略，同时考虑顾客需求、物料投放和交货期等因素的影响，可提高瓶颈资源的使用效率[5]。缓冲区容量和待加工零件的工艺流程、零件在不同加工设备上的加工时间、零件的运输系统、系统设计预算和厂房空间等密切相关，缓冲区容量的设置是否合理将对生产系统的生产费用产生重大影响[6]。

约束理论指出，瓶颈资源的利用程度决定了整个生产系统的生产效率，而较优的缓冲区设置能提高瓶颈资源的使用效率，因此缓冲区设置问题已成为基于虚拟单元生产模型下的制造企业亟需解决的重要问题[7-8]。文献[9]主要针对自动化的生产车间进行研究，利用分解策略来分析求解设备可用度与缓冲区容量之间关系的数学模型，且以生产线最大可用度为优化目标，并利用基于智能交叉算子和智能算子的改进遗传算法对模型进行求解，得到了缓冲区容量分配图。文献[10]对随机过程原理进行深入分析，并把随机过程原理利用于缓冲区容量设置，提出了缓冲区容量与缓冲区被充满概率之间的数学模型，优化缓冲区容量配置标准。由排队论中的利特尔定律(Little'slaw)可知，缩短生产系统的加工周期，最重要的一个方法就是合理控制在制品的总数量，而影响在制品总数至关重要的是要设置合理的缓冲区容量[12]。在生产过程中，各缓冲区容量设置与加工任务数量、设备利用情况等因素相关，因此，如何根据生产过程中的相关资源来优化缓冲区容量，成为有效提升瓶颈资源利用率关键问题。

本文基于前人研究基础上，对虚拟单元生产系统的动态调度进行研究分析，主要是针对生产系统中时间缓冲容量最优为目标，构建缓冲区容量求解模型，并同时以在制品拒绝率、在制品数量和设备的利用率等指标来约束最优的缓冲区容量，运用改进优化后的遗传算法进行运算，最后通过某船厂的实际生产数据，利用仿真软件MATLAB进行模型仿真验证。

1 问题模型

1.1 问题描述

Goldratt的约束理论中指出，通过重点配置瓶颈资源，合理设置系统的缓冲区容量来减少生产过程中出现的波动对瓶颈资源的不利影响，提高瓶颈资源利用率对提高系统整体性能具有重要意义。缓冲区的容量大小问题至关重要，过小会导致工位堵塞，过大又会耽误生产周期和工位的空闲状态。不管是工位堵塞和工位空闲都会使得生产线生产能力不平衡，出现工位负荷分配不均的情况，这在很大程度上影响了生产线的正常运行和生产效率。因此，合理配置缓冲区是生产线设计中的一个关键问题。研究缓冲区时需考虑缓冲容量与缓冲位置之间的关系，通过配置缓冲区，可以使虚拟单元在调度的同时性能达到最优。本文为简化处理，将缓冲位置和缓冲容量联合起来作为一个整体来研究。本文在面向多个加工任务情况下考虑瓶颈资源的情况下，以生产线的缓冲区容量最优为目标，且考虑生产过程中的多个指标值，使得求解的最优的缓冲区容量更符合实际的生产需要。

对于生产过程中瓶颈资源的确定，一般是根据订单来将加工任务进行分批量处理，再针对每道工序上的能力和负荷进行比较，或者通过观察生产过程中每道工序前在制品堆积量的大小来确定。本文主要是通过缓冲区容量的优化来提高瓶颈资源的利用率，因此，本文就采用第二种方式来识别瓶颈，针对这些瓶颈设置好缓冲区后，缓冲区容量大小的设置就成为提高整个生产系统的生产效率的至关重要的问题了。

虚拟单元内的设备可以根据实际的生产需要实时进行重构和重组，准确地识别出生产系统中的瓶颈资源，从而正确地设置缓冲容量，将会对缩短产品生产周期提供有效的保障。缓冲区是按照一定规则进行输入及输出的动态系统，如图1所示，设备和缓冲区的布局如图2，这里选取单元内相邻的三道工序。在生产系统中，设备性能参数用Si(ui,pi,ri)表示，其中ui、pi和ri分别表示设备i的加工速度、故障率和修复率，在t时缓冲区状态用Hi(zi,bi)来表示，zi表示加工设备Si的工作状态，当zi的值分别为z、j和d时，分别表示设备待料、阻塞和加工的状态。bi表示缓冲区Hi时刻t时待加工在制品数量。

图1 虚拟单元输入输出

图2 缓冲区布局图

1.2 条件假设及目标函数

假定进入到单元内加工的在制品有m道工序，每个设备的加工能力都不一样，虚拟单元内应包括n台机器设备，设置瓶颈设备的缓冲区，任务进入到单元内的第一道工序加工，直到所有的工序加工完毕，并假设条件如下：①加工对象到达缓冲区服从泊松分布；②当进入到单元加工时，将直接进入第一个工序，如果单元内的某一设备正在加工时，则新进入缓冲区的在制品进入列队等待加工；③任务的加工时间服从指数分布(这里包括装夹、准备时间等)；④第一道工序的加工设备不会停工待料，最后一道工序的设备的缓冲区不阻塞。

为了对整个缓冲区布局进行研究，选取第i个缓冲区并对其状态情况进行研究，其状态转移图如图3所示。

图3 缓冲区状态转移图

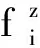
基于以上假设，可以得到虚拟单元考虑瓶颈资源因素的影响的缓冲区容量优化的目标函数为：

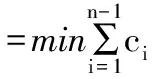
(1)

s.t.

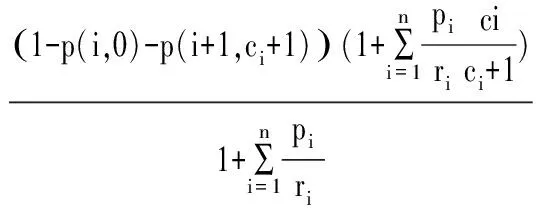
(2)

(3)

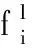
(4)

0≤ci≤ki,i=2,3,…,n-1

(5)

其中，目标函数(1)表示虚拟单元内的所有缓冲区容量优化的目标函数；式(2)表示满足加工设备实际加工能力的方程式，其中Wi为加工设备i实际加工可用度；式(3)表示第一道工序的加工设备不存在待料情况和最后一道工序的加工设备不出现阻塞现象；式(4)表示缓冲区在制品增量概率、缓冲区在制品减量概率、设备加工在制品阻塞概率和设备加工在制品恢复概率；式(5)表示缓冲区容量为非负数。

模型符号说明：ci—表示缓冲区i的容量，ri—表示设备i的修复率，p(i,0)—表示设备处于待料状态，p(i+1,ci+1)—表示设备处于阻塞状态，ki—表示缓冲区预计的最大值。

由于缓冲区容量问题是一个随机的、决策向量整数非线性的规划问题，可以采用多个生产过程中的指标共同确定缓冲区容量问题，如在制品数量N、模型中设备利用率U和模型中在制品平均拒绝率R三个指标。指标方程如下：

(6)

(7)

(8)

式(6)表示在制品数量；式(7)表示设备平均利用率；式(8)表示在制品的平均拒绝率。

通过上述三个性能指标能够反应出系统的均衡负荷状态，并且通过优化节点处的缓冲区大小来获得较好的均衡负荷系统。本文以最优的缓冲区容量为目标，通过上述模型和分析，可以求出系统的性能指标。

2 基于改进遗传算法的缓冲区容量计算

遗传算法是模拟生物进化过程形成的具有全局搜索能力的一种算法[13]。在遗传算法过程中，适应能力较好的父辈将存活，并通过遗传、交叉、变异等操作把较好的基因传递给下一代，使下一代具有更强的适应能力，通过不断反复迭代进化，群体将逐渐产生更优良的种群，以更好的适应环境变化。

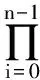
在遗传算法中，染色体编码和交叉是算法的关键部分，本文将采用自然数编码和改进交叉算子来提高算法精确度和效率。

2.1 染色体编码

编码可以通俗理解成把生产实际变量转换为遗传算法可以识别的染色体，满足遗传算法后期的遗传、交叉和变异操作，因此，生产实际变量应和染色体成一一对应关系。根据遗传算法常用编码方式特点，本文采用自然数编码，即随机产生染色体数，使染色体产生具有随机性，同时又必须保证染色体在约束范围内，确保染色体具有意义。图3为本文基于自然数编码规则而形成的种群初始单个染色体，其中xi为染色体中第i个基因值，表示第i个缓冲区内最大在制品数量ci；n为染色体中基因数量，表示虚拟单元中缓冲区数量对应。为了确保所生产的染色体具有意义，染色体必须满足以下条件。

图4 染色体编码规则

(1)xi不大于第i个缓冲区限定的最大数量；

(2)在第一步基础上，按照式(9)产生自然数填入对应的基因位置；

xj=「(xjmax-xjmin)×rand+xmin

(9)

式中「为取上整函数，xj为个体第j个基因取值，xjmaxw为第j个基因最大值，xjmin为第j个基因最小值，rand为[0，1]内的随机数。

(3)重复上述步骤k次，产生k个初始种群大小。

2.2 智能交叉算子

交叉算子是在父代优秀染色体中进行交叉操作，产生更多优秀的后代。传统的交叉算子在进化期间保持不变的交叉率，容易破坏群体全局性、多样性，使算法陷入早熟现象，导致算法收敛进程和搜索效率降低。智能交叉算子能够根据进化次数和染色体适应度的不同，自动调整交叉算子的交叉率。由于每个缓冲区对应着相应的加工设备，不同的加工设备会影响对应的缓冲区，传统的单点交叉和部分匹配交叉都破坏缓冲区和相应加工设备之间的关系，因此本文采用采用半父体交叉策略，不仅继承了父体信息，还保证缓冲区和加工设备之间的关系。图为第i次进化后的种群个体，通过计算每个个体的交叉率，决定个体交叉顺序，如图5所示，选取序号为4和8的染色体进行半父体交叉。交叉率根据式(10)来确定：

(10)

式中，bcmax为最大交叉率，即初始交叉率，bcmin为最小交叉率，即最终交叉率，Fp为平均适应值，F(xi)为目前最大适应值。

图5 改进交叉算子求解图

3 实例验证

3.1 瓶颈缓冲区容量优化结果

本章以某船舶制造企业的生产实际数据为例，对本文提出的方法进行验证，设备和零件工艺的关系及设备性能参数如表1所示。由于有的工序具有被多台设备同时加工的能力，导致在制品加工出现很多不可控因素，要求优化后的工艺路线使缓冲区容量最少及完工时间最短。

用MATLAB仿真软件对大量的实际生产数据进行仿真，得到在制品拒绝率和节点容量的关系，如图6所示。

图6 缓冲区容量、在制品拒绝率和在制品数量关系图

图7 原生产调度甘特图

图8 优化后生产调度甘特图

从图6中可以看出，当缓冲区的容量很小的时候，在制品的拒绝率比较高。随着缓冲区容量的增加，在制品的拒绝率迅速减小，但随后在制品的减小率变得越来越小。当节点缓冲区容量和为0时，在制品拒绝率为36.21%，当节点缓冲区容量和为40时，在制品拒绝率为12.62%，当节点缓冲区容量和为80时，在制品拒绝率为3.41%。在制品的拒绝率在节点缓冲区0～50之间下降变化非常大，同时在制品数量却是迅速增加。在企业综合考虑场地、成本及交货期等条件时，从图中可以看出选取节点缓冲区容量和为140，在制品拒绝率为3.41%时比较合适，此时这是时候，在制品总数量为132，因为这个时候在制品的拒绝率和在制品数量和在制品平均在制时间都随着节点缓冲区容量的变化开始变得缓慢。

3.2 缓冲区容量优化后设备调度结果

按照本文的优化方法，以缓冲区容量最优为目标对设备进行调度，原在制品设备调度甘特图如图所示。本文在虚拟单元基础上，充分调用虚拟单元调度灵活性特点，当一个单元内的设备加工完成后便进行释放，以便设备的充分利用，同时采用遗传算法进行运算实验，最大循环次数选取500次，得到优化的后的调度方案，优化后的调度甘特图如图8所示。

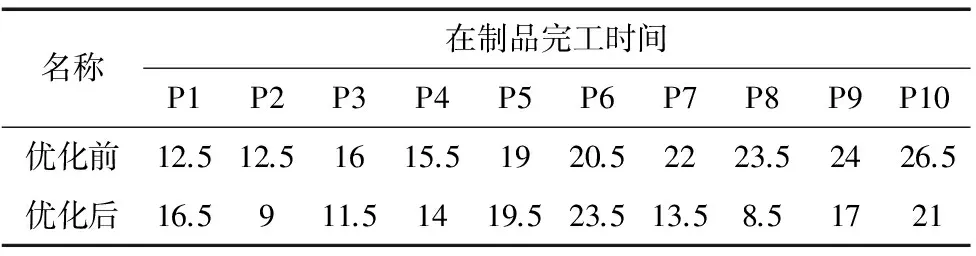
表2 在制品的完工时间

图7表示的调度前的调度甘特图，图8是优化后的在制品调度甘特图，可知，优化后的在制品加工布局不仅有效的减小了在制品最终完工时间，由优化前的26.5h减小到23.5h，节约了12.76%的时间，同时降低了缓冲区总容量，提高了系统运行效率，具有一定的实际意义。

4 结束语

本文针对具有多道连续加工工艺的在制品虚拟单元，多个加工任务同时进行加工时，通过优化缓冲区容量来提高瓶颈资源的利用效率，确定了虚拟单元内缓冲区容量优化的目标函数，并结合生产过程的相关指标共同约束缓冲区容量的设置，利用改进的遗传算法进行迭代运算，最后用MATLAB仿真软件进行模型仿真，确定了缓冲区容量与在制品数量及平均在制品容量等相关指标的关系。在今后的研究中还可以进一步结合事件驱动和周期驱动等因素对虚拟单元内的缓冲区容量进行考虑。

[1]NiteshKhilwanietal.Amethodologytodesignvirtualcellularmanufacturingsystems[J].JournalofIntelligentManufacturing, 2011, 22:533-544.

[2]SaadettinErhanKesen.Amixedintegerprogrammingformulationforschedulingofvirtualmanufacturingcells(VMCs) [J].IntJAdvManufTechnol, 2010，47:665-678.

[3]GoldrattEM,CoxJ.TheGoalaProcessofOngoingImprovement[M] .NY:NorthRiverPress, 1984.

[4] 叶涛锋, 韩文民. 按订单生产方式下的瓶颈资源的确定[J] . 工业工程与管理, 2003, 8(6) : 51-54.

[5] 刘士新, 宋健海, 唐加福. 资源受限项目调度中缓冲区的设定方法[J]. 系统工程学报, 2006,21(4): 381-386.

[6]ZinovyD,Radovisky.AQuantitativeApproachtoEstimatetheSizeoftheTimeBufferintheTheoryofConstraints[J].InternationalJournalofProductionEconomics, 1998,55 (2):113-119.

[7] 万伟,蔡晨.在单资源约束项目中的关键链管理[J].中国管理科学,2003,11(2):70-75.

[8] 张良安，梅江平，黄田.基于遗传算法的机器人自动化生产线缓冲区容量分配方法[J]机械工程学报，2012,46(11)：101-106.

[9] 谭民. 缓冲区容量的优化分配[J].控制与决策, 1992, 7(5):386-389.

[10] 孟凡力，谈大龙,黄雪梅. 装配系统中缓冲区容量的研究[J].计算机集成制造系统，2005,11(11):1609-1615.

[11] 宋士刚. 可重组制造系统缓冲区容量的优化研究[J].计算机集成制造系统,2008,14(10):1951-1956.

[12]YAMASHITAH,SUZUKIS.Buffercapacityallocationforadesiredthroughputinproductionlinestransactions[J].IIE, 1998,30(10):883-892.

[13] 欧阳浩. 用遗传算法解决物流中的仓库选址问题[J]. 制造业自动化,2014,36(1):51-64.

(编辑 李秀敏)

Bottleneck Buffer Allocation Optimization of the Virtual Manufacturing

LVJie，GUOTing-fang，HANWen-min

(SchoolofEconomicsandManagement,JiangsuUniversityofScienceandTechnology,ZhenjiangJiangsu212000,China)

Thispaperdiscussestheproblemofbufferallocation,toreducetheinfluenceinbottleneckresources,whichbassesontheTheoryofConstraintsbottleneckresourcesandmultipleprojectsinprocessingatthesametimeinthevirtualmanufacturingcell.Toestablishthegoalofoptimalbufferallocationforfunctionmodel,andusingtheimprovedgeneticalgorithm,andcombiningwiththeproductrejectionrateinthenumberofproducts,equipmentutilizationandotherindicatorstoevaluatethemeritsofbuffercapacity.Finally,usingMATLABwiththeactualdatatoverifyashipyard,thesimulationresultsdemonstratetheeffectivenessandfeasibilityofthemethod.

virtualcellularmanufacturing;bottleneckresources;bufferallocation;geneticalgorithms

1001-2265(2016)12-0121-04DOI:10.13462/j.cnki.mmtamt.2016.12.033

2016-02-22；

2016-03-25

国家自然科学基金项目：物流平衡下的虚拟单元构建与调度联合决策(71271105)；教育部人文社会科学研究规划基金项目：不确定需求下细胞生产的动态单元构建与调度问题研究(12YJA630036)

吕洁(1973—)，女，陕西汉中人，江苏科技大学副教授，研究方向为统计分析与经济计量，生产运作管理，(E-mail)lvjie0511@126.com。

TH166；TG

A