基于GA-BP网络的数控机床热误差优化建模研究*

魏效玲，张宝刚，杨富贵，姬晓利

(河北工程大学 机电工程学院，河北 邯郸 056038)

基于GA-BP网络的数控机床热误差优化建模研究*

魏效玲，张宝刚，杨富贵，姬晓利

(河北工程大学 机电工程学院，河北 邯郸 056038)

为减小热误差对数控机床加工精度的影响，提出基于GA-BP神经网络的机床热误差优化建模方法。阐述遗传算法(GA)和BP神经网络算法，介绍GA-BP神经网络模型的具体步骤，建立BP神经网络热误差预测模型和GA-BP网络热误差优化模型。运用MATLAB软件对两种模型进行实验仿真，结果表明：GA-BP神经网络的数控机床热误差优化建模方法具有建模时间短、预测精度高、收敛速度快等优点。

热误差；遗传算法；BP神经网络；数控机床

0 引言

随着精密加工技术的快速发展及复杂产品的大量涌现，机床的加工精度备受关注。数控机床在运转过程中，由于加工系统内部及外部各种因素影响而产生加工误差，这些误差严重影响了被加工零件的精度及表面质量[1]。大量研究表明：影响数控机床加工精度的主要误差为热误差，约占机床总体误差的40%～70%[2-3]。目前减小热误差有两种基本方法：热误差预测法和热误差补偿法[4]。预测法是一种“硬技术”，其耗时长、花费大，对于具有时变性、非线性等特点的热误差，实践证明补偿法是一种新型有效的方法。在误差补偿技术中建模是最为关键的环节，模型的精度和鲁棒性直接影响着补偿的效果。目前，常用的热误差建模方法有：人工神经网络建模、模糊神经网络建模、最小二乘法建模、支持向量机建模[5]。文献[6]详细阐述了BP神经网络热误差建模方法，并对其进行了仿真验证分析，但BP神经网络存在学习收敛速度慢、易于陷入局部极小点等缺陷，仿真结果不理想。因此，本文提出基于GA—BP神经网络的数控机床热误差预测建模，采用遗传算法(GA)优化BP神经网络的权值和阈值来建立热误差预测模型，结果表明，GA-BP网络优化模型具有建模时间短、预测精度高、收敛速度快等优点。

1 GA-BP网络算法

1.1 遗传算法

遗传算法是由美国教授J.Holland[7]在1975年第一次提出，它借助于生物进化理论与遗传学原理，依据适者生存、优胜劣汰的原则，模拟生物种群由简单到高级的生物进化过程，从而达到初始解逐渐趋近最优解的目的。它是一种具有全局搜索能力的优化算法，基本要素有:染色体编码、初始群体确定、个体适应度函数选择、遗传操作设计和运行参数设定[8]。

1.2 BP神经网络

BP神经网络是一种多层前馈神经网络，采用误差反向传播训练学习，具有极强的非线性映射能力，是目前应用最广泛的神经网络模型之一[9]。它的拓扑结构包括：输入层、隐含层和输出层[10]，图1为它的结构示意图，Xi(i=1,2,…,m)表示输入值，Yj(j=1,2,…,n)表示输出值，wij为输入层与隐含层的连接权值，wjk为隐含层与输出层的连接权值。

图1 BP神经网络结构示意图

1.3 GA优化BP神经网络算法

遗传算法优化BP神经网络法不仅可以进行全局寻求最优解，而且还能克服BP神经网络法自身的众多缺陷，此种方法已应用于很多领域。遗传算法优化BP神经网络的实质是对BP神经网络权值和阈值进行优化，整个过程的基本思想是：首先用遗传算法全局优化BP神经网络的权值和阈值，满足要求之后再用BP神经网络在极值点附近快速搜索，直到满足要求为止。经过全局寻优与快速搜索的相互配合，不仅提高了整个模型的收敛速度，而且还解决了易于陷入局部极值点等问题。基于GA-BP神经网络的运算流程如图2所示。

GA-BP网络的建模步骤如下：

(1)参数编码 将权值和阈值作为参数变量进行编码，生成初始种群，编码方法选用浮点数编码法。

(2)适应度函数选择BP神经网络的误差平方和越小，网络的性能越好，所以BP神经网络是一个最小化优化问题，故适应度函数可用误差平方和的倒数来表示，即：

(1)

式中，E——网络输出误差；

yi——网络第i个实测值；

(3)选择操作：选取适应度较高的个体，淘汰适应度较低的个体；

(4)遗传操作：通过交叉操作和变异操作生成新种群；

(5)重复步骤(2)～(4)，反复修正网络的权值和阈值，直到满足训练要求为止。

图2 GA-BP神经网络运算流程图

2 机床热误差建模与优化

2.1 选取温度测点

本文以立式镗铣床为研究对象，建立热误差预测模型。选用TEMP14多点温度测量仪测量机床上易受温度影响的4个点的温度值，分别为立柱的前端T1、丝杠轴承端T2、主轴箱前端T3、主轴后端T4，选用电涡流位移传感器测量Z轴轴向热误差。各传感器布置如图3所示。

1.立柱 2.丝杠 3.主轴箱 4.主轴 5.位移传感器 6.工作台 7.温度传感器T18.温度传感器T29.温度传感器T310.温度传感器T4

图3 传感器布置图

实验中，环境温度为25℃，主轴转速为3000r/min，丝杠转速为1000r/min，每2min取样一次，连续取样240min，所得各测点的温度变化曲线如图4所示，Z轴轴向热误差变化曲线如图5所示。

图4 各测点温度

图5 轴向热误差

2.2 BP神经网络建模

本文以试验所测温度值为网络模型的输入，以轴向热误差为目标函数的输出，网络的拓扑结构为4-9-1，隐含层传递函数为tansig，输出层传递函数为purlin,算法训练函数为trainlm。整个BP神经网络的热误差预测模型如图6所示。

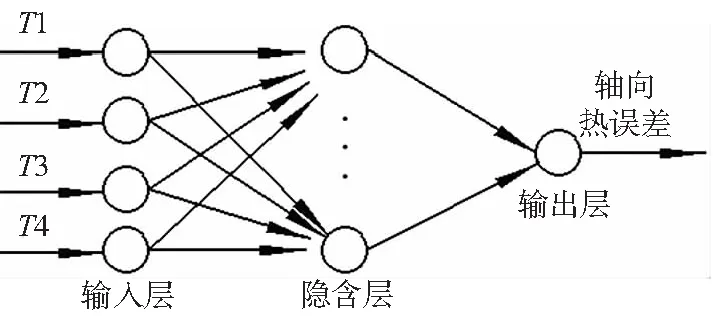
图6 BP神经网络的热误差模型

将测量的120组数据分为两部分，一部分90组作为训练数据，另一部分30组作为测试数据。在整个学习训练过程中，学习率设为0.01，训练输出误差水平为0.0005，最大训练迭代次数为200。运用MATLAB软件训练和仿真，预测结果如图7所示。

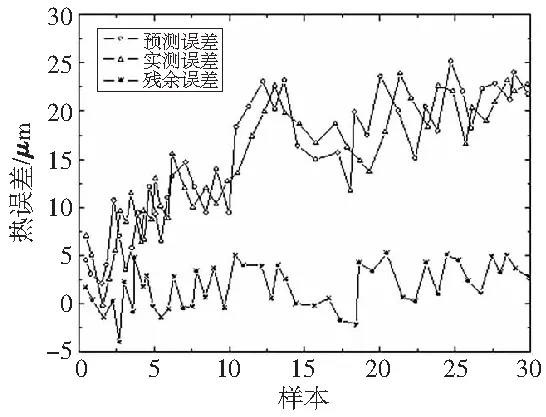
图7 BP神经网络的建模结果

2.3 GA-BP网络建模

同样将测量的120组数据分为两部分，一部分90组作为训练数据，另一部分30组作为测试数据。在整个学习训练过程中，学习率设为0.01，训练输出误差水平为0.0005，交叉操作选用单点交叉方式，种群大小为50，交叉概率取0.1，变异概率取0.01，最大迭代次数为90。预测结果如图8所示。

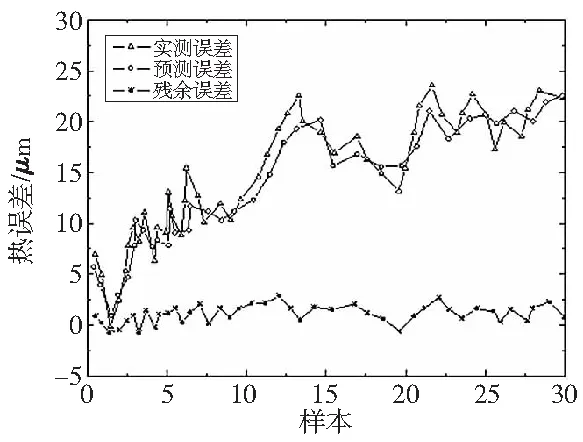
图8 GA-BP网络的建模结果

2.4 两种模型的对比

从图7和图8可以看出，BP神经网络模型的预测值与实验测量值的误差曲线变化趋势基本一致，但数值离散性较大，GA-BP网络模型的预测值与实验测量值的误差曲线吻合性较高，数值相对集中。两种模型的残余误差指标对比如表1所示。从表1可知，BP神经网络模型的残余误差带宽要比GA-BP网络模型的残余误差带宽大5.4510μm，说明后者的误差变动范围小。与BP神经网络模型相比，GA-BP网络模型的残余误差平均值降低了0.8615μm，均方差降低了2.4610μm，说明后者的预测精度高于前者。

表1 两种模型的残余误差指标对比

3 结束语

为研究影响机床加工精度的主要因素热误差，提出基于遗传算法优化BP神经网络的数控机床热误差预测方法，本文以立式镗铣床为研究对象，合理布置温度传感器和位移传感器采集记录相关数据，建立BP神经网络热误差预测模型和GA-BP网络热误差优化模型。经对比，GA-BP网络模型的残余误差宽带、残余误差平均值及残余误差均方差均小于BP神经网络模型，可见GA-BP网络模型的预测精度高于BP神经网络模型。因此将GA-BP网络预测模型用于机床热误差补偿系统可有效减小热误差，提高机床的加工精度。

[1] 杨建国,范开国,杜正春.数控机床误差实时补偿技术[M].北京:机械工业出版社,2013.

[2] 王春暖,秦波.基于改进PSO优化BP的数控机床热误差预测研究[J].组合机床与自动化加工技术,2014(10):70-72.

[3] 魏效玲,张宝刚,陈华,等.高速电主轴传热机理及温度测点优化分析[J].煤矿机械,2015(1):88-90.

[4] 陈泽宇,龚凌云.基于GA—SVR的数控机床热误差建模[J].组合机床与自动化加工技术,2012(2):9-15.

[5] 章婷,刘世豪.数控机床热误差补偿建模综述[J].机床与液压,2011,39(1):122-127.

[6] 孙勇,曾黄磷.一种新的数控机床热误差实时补偿方法[J].机械设计与制造,2010(1):244-245.

[7] 雷英杰,张善文,李续武,等.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2005.

[8] 赵海涛.数控机床热误差模态分析、测点布置及建模研究[D].上海:上海交通大学,2006.

[9] 张鑫星.龙门加工中心的热误差分析及神经网络建模[D].南宁:广西大学,2012.

[10] 富春丽,芮执元,刘军.数控机床电主轴热误差的预测方法[J].兰州理工大学学报,2012,38(1):28-31.

(编辑 李秀敏)

Research on Optimization Modeling of CNC Machine Tools Thermal Error Based on GA-BP Neural Network

WEIXiao-ling，ZHANGBao-gang，YANGFu-gui，JIXiao-li

(CollegeofMechanicalandElectricalEngineering,HebeiUniversityofEngineering,HandanHebei056038,China)

InordertodiminishtheinfluenceofthermalerroronmachiningaccuracyofCNCmachinetools,anoveloptimizationmodelingforthermalerrorinmachinetoolsisputforwardbyGAtooptimizeBPneuralnetwork.ThispaperhaselaboratedgeneticalgorithmsandBPneuralnetwork,introducedthespecificstepsofgenetictooptimizeBPneuralnetwork,buildpredictmodelwiththethermalerrorofBPneuralnetworkandoptimizedmodelwithGA-BPnetwork.ThesimulationresultsconductedonMATLABshowsthattheGA-BPmethodperformsfarbetterthanBPneuralnetworkintermsofthemodelpredictionaccuracyandrateofconvergence.

thermalerror;geneticalgorithms;BPneuralnetwork;CNCmachinetools

1001-2265(2016)12-0100-03DOI:10.13462/j.cnki.mmtamt.2016.12.027

2016-01-24；

2016-02-25

国家自然科学基金资助项目(61240050)

魏效玲(1963—)，女，山西河津人，河北工程大学教授，研究方向为数控技术与机械制造技术，(E-mail)wxlsm@163.com；通讯作者：张宝刚(1989—)，男，陕西宝鸡人，河北工程大学硕士研究生，研究方向为机械制造及其自动化，(E-mail)wnpuzbg@163.com。

TH161；TG

A