基于EMD-MPE与HMM的滚动轴承故障诊断*

0 引言

滚动轴承作为旋转机械系统的重要组成部分，其能否健康工作关系着整个系统的正常运行[1]。所以，对出现故障的滚动轴承及时诊断显得尤为重要，而实现准确诊断的一关键因素在于对故障轴承信号中进行有效地处理。常见的滚动轴承故障诊断方法有傅里叶变换(FFT)，小波变换，希尔伯特变换等，但它们都有各自的缺点和不足。如傅里叶变换的时频窗口固定不变的缺点导致其无法满足对滚动轴承的非平稳振动信号进行自适应分解[2]；小波变换虽然有可变的时频窗口，但其本质上是通过该窗口对信号进行机械性地分割，同样也不是一种自适应的信号处理方法[3]；希尔伯特变换(HHT)在机械故障诊断领域得到了广泛的应用，但其存在包络过冲与欠冲、端点效应等问题[4],故其理论上仍需进一步完善。以上信号时频分析方法都是将非线性信号分解为平稳信号，这样的“转换”难免有一定的局限性[5]。对非线性信号运用非线性分析方法进行分析可以有效地避开时频分析方法的局限，从而直接提取滚动轴承的故障信息。

多尺度排列熵[6](Multi-scale Permutation Entropy, MPE)作为一种检测时间序列随机性和动力学突变行为的非线性分析方法，具有计算速度快，抗噪能力强，适合在线监测等优点[7]。Aziz W、Arif M等[8]提出了多尺度排列熵的概念，通过与多尺度熵进行对比分析生理信号表明，对振动信号进行多尺度分析是一种有效方法。Yan、Liu等将排列熵(PE)应用于旋转机械系统振动信号的特征提取，并与近似熵、Lempel-Ziv的复杂度进行比较，取得了很好的试验效果[9]。隐马尔科夫模型(Hidden Markov Model, HMM)是一种基于时间序列的统计模型[10]，其能够对输入的信息进行建模和分类，已在语音信号中得到了广泛的应用[11-12]。Fatih Camci等[13]将HMM应用到机械系统中，对钻头的健康状态进行诊断取得了很好的效果。故本文提出了基于EMD-MPE的滚动轴承故障信号特征提取方法，并将信号特征输入HMM模型库进行状态识别。在此基础上，与支持向量机(Support Vector Machine, SVM)进行对比研究。

1 EMD-MPE与HMM滚动轴承故障诊断模型

EMD-MPE与HMM滚动轴承故障诊断模型运用非线性分析方法-多尺度排列熵来直接检测振动信号不同尺度下的动力学特性，并选择合适尺度因子下的排列熵值作为特征向量输入HMM模型库进行故障类型判别，其具体过程如图1所示。

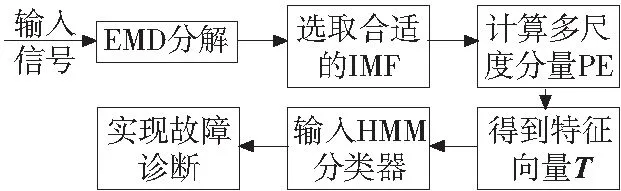
图1 EMD-MPE与HMM滚动轴承故障诊断流程图

首先，将采集的原始振动信号进行EMD降噪分解，由于分解过程中端点效应、滑动步长的选取以及循环终止条件的选取等因素的影响容易产生虚假分量，即EMD分解过程中产生的IMF存在非原始分量分解的结果，故对所有IMF求取相关系数，并选择系数较大的IMF作为特征信号；而后计算特征信号的多尺度排列熵并选取特征向量T，最后输入HMM模型库进行故障判别。

1.1 基于EMD-MPE滚动轴承故障特征提取

EMD是一种用于非线性、非平稳的信号分析方法[14]，它能自适应地将复杂信号分解为一系列不同频段的本征模态函数(Intrinsic Mode Function, IMF)，通过选取合适频段的IMF进行信号重组以此达到滤波降噪的目的，此方法已被广泛应用在故障诊断中[15]。

MPE是一种检测时间序列随机性和动力学突变行为的非线性分析方法，它对信号的突变十分敏感。对于滚动轴承故障信号，不同的故障类型其内部的动力学突变行为也不同[16]，故可以依赖MPE的敏感特性对故障类型进行特征提取。其具体过程如下:

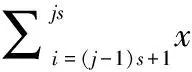
(1)

式中，s为尺度因子，ys(j)为不同尺度下粗粒化时间序列。根据公式(1)可以看出，当s=1时粗粒化时间序列即为原始时间序列，即单尺度排列熵。

(2)对不同尺度下的时间序列进行排列熵计算，得到公式(2)，其中P1,P2,…,Pk,k∈N是每一种符号序列出现的概率。

Hp(m)=-∑m!j=1PjlnPj

(2)

式中，0≤Hp(m)≤ln(m!),当Pj=1/m!时，Hp(m)有最大值ln(m!)。通常，对Hp(m)进行归一化处理，即

Hp=Hp(m)/ln(m!)

(3)

上式可以看出0≤Hp≤1。Hp值得大小反映了信号的复杂度和随机程度。Hp值越大反映信号越随机，反之，则说明信号越规则。Hp值得变化反省和放大了时间序列的局部微小变化。

1.2 HMM模型库状态识别

HMM是一种基于时间序列的统计模型，适用于动态时间序列，尤其是对于非平稳、低重复性和复现性的信号具有很强的模式识别能力，并且它对离散输入信号特征具有识别效率高、速度快等优点[17]。

将经过EMD-MPE方法提取的特征向量T输入HMM模型库进行训练，待每个模型训练收敛后，向模型库输入验证样本进行状态识别，模型输出的似然概率值最大所对应的模型状态即为滚动轴承的带诊断状态。

2 试验分析

试验所用的滚动轴承是型号为N1004的圆柱滚子轴承，其内径、外径、滚珠直径以及节径分别为20mm、42mm、5.5mm以及31mm，滚子数目为12个。试验分别采集轴承正常状态(NORM)、内圈故障(Inner Race Fault，IRF)、外圈故障(Out Race Fault, ORF)、滚子故障(Rolling Element Fault, REF)四类状态信号，每类样本共40组，每类前20组为训练样本，后20组为验证样本，采样频率为10k，轴承转速为700n/min，采样点数为2048。滚动轴承内圈故障、外圈故障、滚子故障以及正常状态信号的时域波形如图2所示。

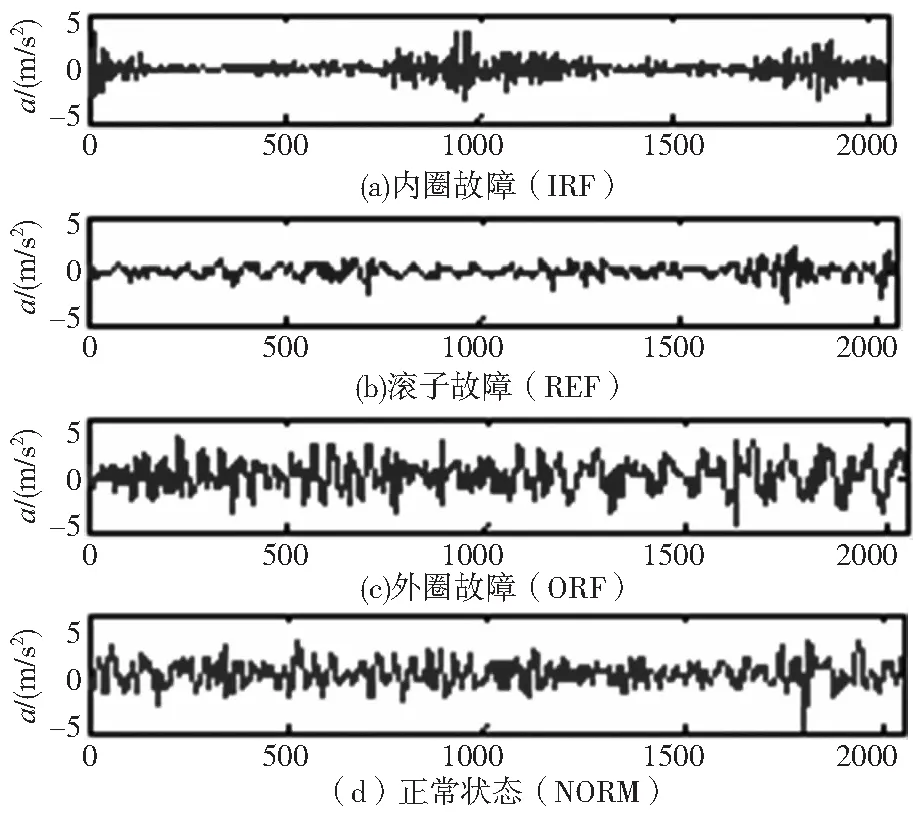
图2 正常与故障状态轴承振动信号时域波形

由于滚动轴承在运行过程中，不同状态下其内部动力学特性不同，故其4种状态振动信号在时域波形存在差异，在时域波形中具体表现为幅值大小不同，如果滤除噪声的干扰在某些规律时段内波形的幅值点会出现“堆积”。

将每类状态信号进行EMD降噪，为了不赘述本文随机选取内圈故障样本作说明，其EMD分解结果如图3所示。

图3 内圈故障信号经EMD分解

通过图3可以发现，EMD将复杂信号分解为一系列频率从高到低的IMF，而前几个IMF在原始信号中所占的比重较大，一般选取这些IMF来重组信号。针对内圈故障信号，这里选取前4个IMF进行重组，得到降噪后的信号如图4所示。

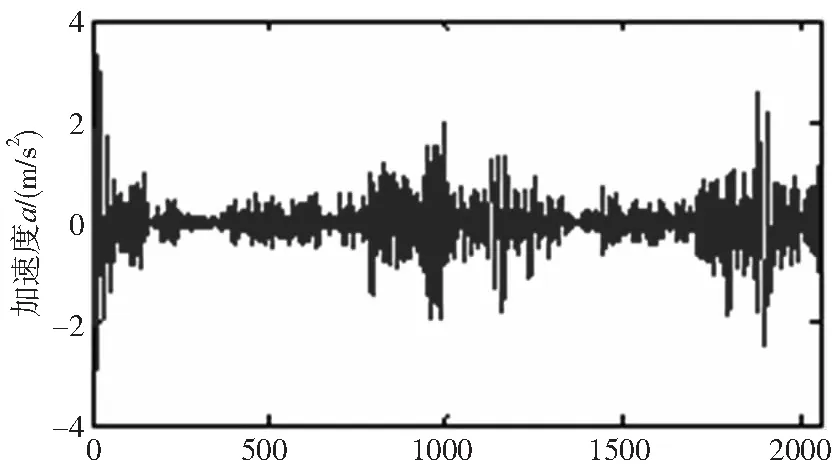
图4 内圈故障信号降噪后时域波形

通过图2a、图4两图对比可以看出，经过EMD分解后的内圈故障信号在时域中的故障显示比较明显，这对后续的求取MPE的熵值具有重要的作用。

将4类状态信号进行MPE分析，并将MPE画成尺度因子的函数，这里嵌入维数m=6，时延λ=1，结果如图5所示。

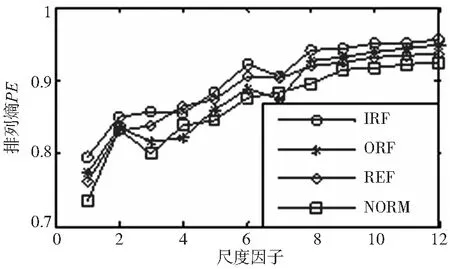
图5 正常与故障轴承振动信号的多尺度排列熵

由图5可以看出，随着尺度因子的增大，排列熵值也随之增大，而熵值越大表明信号越随机，包含的故障信息就越多，所以这里选取尺度因子s=8～12下所对应的PE值作为信号的特征向量并输入HMM模型库进行训练。其中NORM、IRF、ORF和REF的前20组故障样本分别输入正常状态分类器HMM1、内圈故障分类器HMM2、外圈故障分类器HMM3以及滚子故障分类器HMM4四个特定分类器进行训练；一般训练19次左右模型达到收敛状态。最后，将每类剩余的20组验证样本的特征向量输入分类器库进行验证并由HMM模型分类器库输出似然概率，似然概率最大值所在的模型即对应故障状态。HMM1、HMM2、HMM3、HMM4分类器对应四类验证样本判别结果如图6～图9所示。

图6 EMD-MPE与HMM模型对内圈故障的识别

图7 EMD-MPE与HMM模型对外圈故障的识别

图8 EMD-MPE与HMM模型对滚子故障的识别

图9 EMD-MPE与HMM模型对正常状态的识别

图6～图9四幅图形为HMM分类器分别对滚动轴承内圈、外圈、滚子以及正常状态进行分类的结果，每类20个验证样本分别输入4个分类器并输出对数似然概率，每个样本所在分类器输出的似然概率值最大即为该样本所在的故障状态。例如，对于内圈故障而言，其在HMM1中输出的似然概率值比其他状态样本在HMM1中输出的概率值比其他状态样本输出的概率值要大，即判断正确；而其在HMM2、HMM3、HMM4分类器中输出的似然概率则比其他状态样本输出的值小；同样，外圈、滚子以及滚子状态验证样本在HMM2、HMM3、HMM4分类器中似然概率值多数比其他状态样本输出的概率值大，而概率大的样本所在模型的状态即为故障状态。可以看出分类器中每个对应的故障模型对滚动轴承故障的判别率较高。为了说明EMD-MPE与HMM模型的可靠性，用其去EMD-MPE与SVM模型进行比较研究。

SVM是在统计学习理论的VC维理论和结构风险最小化原理基础上建立的机器学习方法，它克服了“维数灾难”和“过学习”问题，并具有很好的泛化能力，对解决小样本问题具有独特优势[18]。将上述提取的特征向量输入SVM模型中进行故障判别，结果如表1所示。

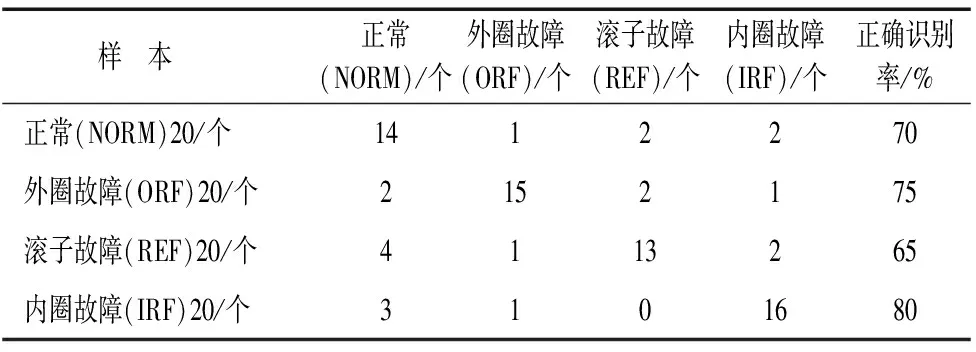
表1 EMD-MPE与SVM故障诊断模型识别结果

通过图6～图9与表1对比可以看出，EMD-MPE与HMM模型对滚动轴承的状态识别率达到了95%以上，错误次数只有1次，有的识别率甚至达到了100%，而EMD-MPE与SVM故障模型的识别率则相对较低，错误次数有的达到了5次，故障识别率只达到了70%左右。试验比较结果表明基于EMD-MPE与HMM滚动轴承故障诊断模型相对EMD-MPE于SVM故障诊断模型更适合于滚动轴承状态识别。

3 结束语

针对滚动轴承故障特征提取和故障识别困难的问题，提出了基于EMD-MPE与HMM的滚动轴承故障诊断模型方法，该模型通过EMD滤波降噪后经过MPE直接分析滚动轴承不同故障状态的动力学突变行为，并且HMM模型具有较好的模式识别能力，将EMD-MPE处理后所提取的特征向量输入HMM模型中进行状态判别，实现滚动轴承故障诊断。试验结果经过与SVM对比研究表明，基于EMD-MPE与HMM的滚动轴承故障诊断方法具有很强的实用性和有效性。

[1] Tian Y, Ma J, Lu C, et al. Rolling bearing fault diagnosis under variable conditions using LMD-SVD and extreme learning machine [J]. Mechanism Machine Theory, 2015,90: 175-186.

[2] Cohen L. Time-frequency Distribution-A Review[J].Proceedings of the IEEE, 1989, 77 (7):941-981.

[3] 徐康,黄民. 基于EMD和DHMM的刀具故障诊断[J]. 组合机床与自动化加工技术,2016(7):89-91.

[4] 阮有兴(Nguyen Huu Hung). 基于希尔伯特—黄变换的移动荷载作用下桥梁健康监测方法研究[D].长春:吉林大学,2013.

[5] 郑近德,程军圣,杨宇. 多尺度排列熵及其在滚动轴承故障诊断中的应用[J]. 中国机械工程,2013,24(19):2641-2646.

[6] 姚文坡,刘铁兵,戴加飞,等. 脑电信号的多尺度排列熵分析[J]. 物理学报,2014,63(7):427-433.

[7] 郑近德,程军圣,杨宇. 基于LCD和排列熵的滚动轴承故障诊断[J]. 振动.测试与诊断,2014,34(5):802-806,971.

[8] Aziz W,Arif M. Multiscale Permutation Entropy of Physiological Time Series [C]//Proceeding of IEEE International Multi-topic Conference, INMIC, 2005.

[9] Yan Ruqiang,Liu Yongbin, Gao X. Permutation entropy: a nonlinear statistical measure for status chararcterization of rotary machines[J].Mechanical Systems and Signal Processing，2012，29(5):474-484.

[10] 吴军，邵新宇，邓超.隐马尔科夫链模型在装备运行可靠性预测中的应用[J].中国机械工程,2010,21(19):2345-2349.

[11] 袁里驰. 基于改进的隐马尔科夫模型的语音识别方法[J]. 中南大学学报(自然科学版),2008,39(6):1303-1308.

[12] 苗苗,马海武. HMM在语音识别系统中的应用[J]. 现代电子技术,2006,29(16):64-66.

[13] Camci F, Chinnam R B.Health-state estimation and prognostics in machining processes[J].IEEE Transactions on Automation Science and Engineering, 2010,7(3):581-597.

[14] 胡爱军,孙敬敬,向玲. 经验模态分解中的模态混叠问题[J]. 振动.测试与诊断,2011,31(4):429-434.

[15] 孔国杰,张培林,徐龙堂,等. 基于经验模态分解的自适应滤波算法及其应用[J]. 信号处理,2009,25(6):958-962.

[16] 王余奎,李洪儒,叶鹏. 基于多尺度排列熵的液压泵故障识别[J]. 中国机械工程,2015,26(4):518-523.

[17] 李志农,蒋静,唐高松,等. 旋转机械故障诊断中的EMD-HMM识别方法研究[J]. 矿山机械,2007,35(12):117-120.

[18] 万鹏,王红军,徐小力. 局部切空间排列和支持向量机的故障诊断模型[J]. 仪器仪表学报,2012,33(12):2789-2795.

(编辑李秀敏)

Fault Diagnosis of Rolling Bearing Based on EMD-MPE and HMM

HE Bin,LIU Quan

(School of Mechanic and Electric Engineering, Beijing Information Science & Technology University, Beijing 100192,China)

Aiming at the faulty signal of rolling bearing being featured and the fault states being classified difficultly, the method of fault diagnosis for rolling bearing based on EMD-MPE and HMM is applied to this paper. Firstly, the vibration signal is decomposed into various values of permutation entropy (PE) based on multi scaling factor by MPE after EMD denoising. It’s necessary to extract the larger values corresponding to the scaling factor as the feature vectors. Finally, the feature vectors are input into the trained HMM for recognition. The experimental results show that the method of EMD-MPE and HMM is superior to the method of EMD-MPE and SVM, and it can identify the fault states of rolling bearing accurately and effectively.

rolling bearing; fault diagnosis; EMD;MPE; HMM

1001-2265(2016)12-0076-04

10.13462/j.cnki.mmtamt.2016.12.021

2016-08-09；

2016-09-20

国家自然科学基金项目(51275052)；国家科技重大专项“高档数控机床与基础制造装备”(2013ZX04011-012)

贺彬(1990—)，男，安徽淮北人，北京信息科技大学硕士研究生，研究方向为机电系统状态监测与故障诊断，(E-mail)452475973@qq.com。

TH117;TG506