肿瘤微阵列数据的小波模极大值特征提取

陈小梅

（福建农林大学，福建 福州 350002）

肿瘤微阵列数据的小波模极大值特征提取

陈小梅

（福建农林大学，福建 福州 350002）

本文提出针对肿瘤微阵列数据的小波模极大值特征提取方法。首先求两类数据的Bhattacharyya距离分布，初步提取特征基因；接着进行小波分解，在频域上用小波分解高频系数检测基因突变点，低频系数逼近表征原始信号特征；然后通过理论分析和构建SVM分类器，经过多次实验选取小波基和尺度，提取特征基因。将该算法应用于数据集(1999年Golub所用ALL和AML)，从中提取了5个基因，分类测试准确率可达94．12%。可见该算法具有较高的可行性与有效性，能为肿瘤间差异基因研究提供一定参考。

微阵列数据；小波模极大值；SVM

1 引言

基因芯片进行癌症诊断极大地提高了数据获取效率，但基因芯片数据存在高维数、高噪声、高通量等特点，如何从基因芯片的海量数据中提取有用的生物学信息，是癌症基因检测的关键。

基因表达水平信号变化极不规则，但其奇异点和不规则的突变部分经常携带比较关键的信息[1]。小波分析理论可以用于基因芯片数据的处理，小波分解后的系数能表征基因表达相关信息[2,3]。文献[4]和[5]分别采用小波分解的低频系数和高频系数作为特征进行分类，分类效果均可以达到93%左右，低频系数特征提取结果总体上好于高频，但没有阐述提取多少个基因，提取的基因是什么，且分类准确率还有待提高。本文提出一种基于小波模极大值的特征提取算法，可以从经典数据集中提取5个特征基因，分类测试准确率达到94.12%。

小波变换理论最早是20世纪80年代初法国地球物理学家Morlet在分析地球物理信号时，提出来的一种数学工具。它是为克服傅里叶分析时域不能局部化，难以检测信号发生突变时间(或位置)的不足而提出的一种信号分析手段。一般情况下，在低频部分(平稳部分)具有较低的时间分辨率和较高的频率分辨率，而在高频部分(细节部分)较高的时间分辨率和较低的频率分辨率，可见小波分析理论适合于探测正常信号中出现的反常现象。而肿瘤微阵列数据突变基因的检测正属于这种从正常信号中探测异常现象的问题。

小波变换模极值点突变点检测原理：模极大值突变点检测是在不同尺度上先对信号进行光滑，再由光滑后信号的一阶和二阶导数检测信号的突变点。

2 小波变换模极大值特征提取算法

肿瘤基因微阵列数据一个显著的特点是样本少，维数高，基因集只有一小部分基因与肿瘤分型有关，可以首先对基因集进行初步的筛选。信噪比是由Golub提出的评价基因对肿瘤分型影响大小的经典准则[6]。但这种准则存在有一定的缺陷，比如当两种类型肿瘤的分布均值相同时，其信噪比d=0，但可能两者的分布波动区别较大，此时的基因可能会被剔除，进而影响差异基因的提取。Bhattacharyya距离既体现了基因在两个类别中均值的差异对样本分类的贡献，又体现了方差的不同对不同分类的影响[7]。所以本文采用基因的Bhattacharyya距离来评价基因中蕴含的分类信息，对基因集进行初步提取。

针对一包括两类肿瘤的微阵列数据矩阵，利用高频分量中的局部极大值点来初步确定基因可能突变位置，然后综合考虑训练样本的可能突变位置，确定这两类肿瘤基因的可能突变点。最后根据突变点位置，提取突变点位置的低频信息作为特征，构建SVM分类器分类测试，具体算法如下：

(1)先根据Bhattacharyya距离及其分布，提取两类间距离较大的基因，对训练数据进行初步降维。Bhattacharyya距离公式为

其中B为两肿瘤基因之间的Bhattacharyya距离，μ1和μ2分别为两类肿瘤某基因表达水平的均值，σ1和σ2分别为两类肿瘤某基因表达水平的标准差。

(2)分别对训练子集的所有样本的基因表达信号进行小波变换处理。

(3)对小波变换处理得到的高频成分利用小波模极大值原理进行突变点位置检测，并将每个样本的局部模极大值点令为1，否则为0。

(4)分别统计两类肿瘤训练集中每个基因可能是突变点出现的次数，求出每个基因可能为突变点的概率。

(5)设定阈值TH，分别将两类肿瘤中概率大于阈值TH的基因提取出来作为候选特征基因。

(6)取两类肿瘤所选基因突变点的并集，并选取所选突变点位置对应的基因的小波分解的低频部分作为特征。

(7)利用训练集中提取的特征构建SVM分类器，利用测试集测试分类器性能。

其流程图如下：

图1 小波变换模极大值特征提取流程图

3 实验分析

为验证本文设计方法的有效性，文章选用一个含有7129个基因的常用数据集(Golub et al，1999年)，该数据集包含38个训练样本(27个ALL、11个AML)和34个测试样本(20个ALL、14个AML)。对原始数据进行缺失值处理、对数处理后，得到一个7129×72的矩阵，作为待处理数据。

3.1 Bhattacharyya距离初步过滤基因

文章首先求出利用Bhattacharyya距离公式，求出AML和ALL各基因之间的Bhattacharyya距离，构建直方图(如下图2)，选取阈值为0.2，从7129个基因中选取了757个候选特征基因。

图2 Bhattacharyya距离初步过滤基因直方图

3.2 小波基函数及尺度选取

本文利用小波变换检测基因表达信号的奇异性，主要是为了确定信号的奇异点位置，应选择合适的小波函数和尺度大小。如果选择的尺度太小，则时间域所选择的时间间隔较小，受噪声的干扰较大；如果尺度太大，则信号突变点邻域的小波变换的模极大值的幅度衰减较快，这使信号的突变点不明显[8]。由于低层小波分解间断的时间间隔较短，包含了频率较高的成分，所以高频系数有较大的幅值。所以文章选择1～5层对不同的小波基进行分解分析。

小波基的选择非常重要，利用不同的小波基函数对信号进行分解，可以突出不同的信号特征。小波基的正则性主要影响小波系数重构的稳定性，通常要求小波基函数具有一定的正则性(光滑性)。样条小波和Daubechies小波都具有较好的正则性。其中样条小波是一种非紧致正交的对称小波，且具有线性相位的特性，但由于非紧致小波会形成无穷长滤波器，如果进行截断，就会产生一定的截断误差。而Daubechies小波是紧致正交基，具有很好的正则性，有利于信号的分解与重构。

肿瘤微阵列数据特征提取问题是奇异点检测问题。在分析奇异信号时，一般选取消失矩较高阶数的小波基，让信号中平滑部分的高频系数趋于0，从而保留高频中的突变部分[9]。小波基的消失矩与Lipschitz指数密切相关，但突变信号的Lipschitz指数一般在0-1之间，因此所选择的小波基的消失矩也不能太高。所以本文选择Daubechies构造的具有很好紧致性的小波基db1，db2，db3比较说明。

3.3 实验结果

经过实验，选择小波基函数为'db3'，分解层数为4，进而利用提取的特征基因子集，构建线性SVM分类器并进行测试，得到如下表不同阈值TH下的测试结果。

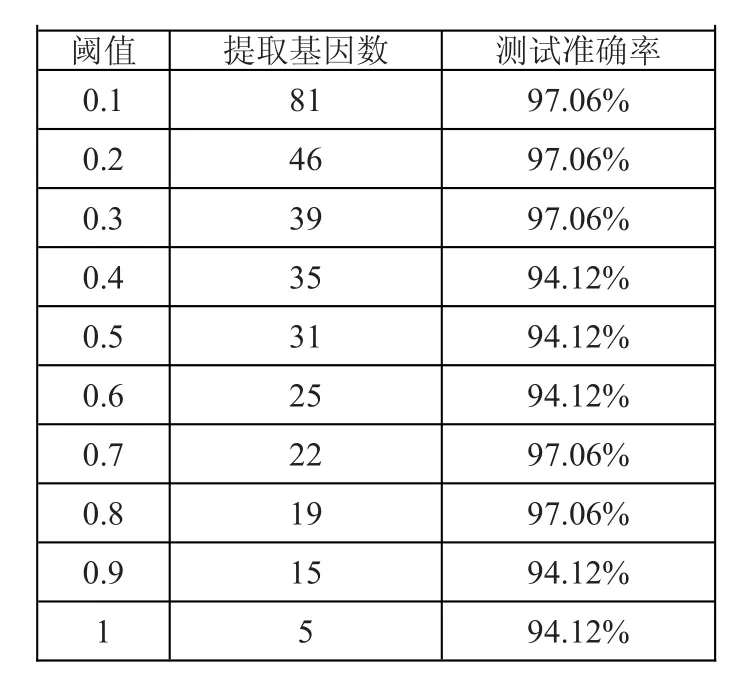
表1 不同TH阈值的测试结果

可见，随着阈值TH的变化，虽然提取的基因数发生了相应的变化，但是测试的准确率比较文档，都达到了94%以上。当选择阈值为1时，该方法所提取的基因只有5个，在GEO中的登录号分别为KIAA0101 gene、UBL1 Ubiquitinlike protein、RanBP2(Ran-binding protein 2)、Cadherin-15、Phosphatidylinositol-glycan-class C(PIG-C)，这时测试的准确率达到94.12%。

4 结果分析

本文针对常用数据集所提取的基因没有出现在文献[6]所提取的50个基因中，但该文献在对34个测试样本进行独立测试时，其准确率只达到了85.29%(29/34)，可见该文献所提取的基因并没有完整的分类信息。文献[10]采用浮动顺序搜索算法搜索特征空间生成候选特征子集，最后选择了5个特征基因构建SVM进行分类，结果也很好，准确率达到了100%，但在该文章中采用的是留一法进行测试，其分类器所具有的泛化能力可能比较不具有说服力。而本文所提取的5个基因，在针对34个测试样本进行测试时，准确率达94.12%，因为可能存在一些比较特别的样本。可见基于小波模极大值特征提取方法具有很好的可行性和有效性，能将其应用于其他肿瘤分类数据中，研究肿瘤基因间的差异基因。

[1]张引红，吴胜举．鼾音信号奇异点检测的小波变换分析方法[J]．计算机工程与应用，2008，44(005)：232-234．

[2]Liu Y．Feature extraction for DNA microarray data in Proc[C]．20thIEEE International Symposium on computer-Based Medical Systems，2007：371-376．

[3]葛哲学，陈仲生．Matlab时频分析技术及其应用[M]．北京：人民邮电出版社，2006．

[4]刘玉杰，刘毅慧．基于小波低频系数基因芯片数据的特征提取[J]．生物信息学，2011，09(3)：255-258．

[5]刘玉杰，刘毅慧．基于小波高频系数基因芯片数据的特征提取[J]．生物信息学，2011，09(4)：339-343．

[6]Golub T R，Slonim D K，Tamayo P，et al．Molecular classification of cancer：class discovery and class prediction by gene expression monitoring [J]．Science，1999，286(5439)：531-537．

[7]李泽，包雷．基于基因表达谱的肿瘤分型和特征基因选取[J]．生物物理学报，2002，18(4)：413-417．

[8]Li S，Liao C，Kwok J T．Wavelet-based feature extraction for microarray data classification[A]．IEEE，2006：5028-5033．

[9]魏宝琴，李白萍．最优小波基的选取原则[J]．甘肃科技，2007，23 (010)：42-43．

[10]李颖新，刘全金，阮晓钢．急性白血病的基因表达谱分析与亚型分类特征的鉴别[J]．中国生物医学工程学报，2005，24(02)：240-244．

Feature Extraction Base on Wavelet Modulus Maxima for Microarray Data

Chen Xiaomei
(FujianAgriculture and Forestry University,Fuzhou 350002,Fujian)

A new method of microarray data to extract features based on wavelet modulus maxima is proposed in this paper. First of all,the Bhattacharyya distance distributions of two classes are derived,preliminarily extracting feature genes.Then wavelet decomposition is adopted to detect the gene mutation of high frequency coefficient,and to approximate the original signal characterization based on low frequency.Finally the features are extracted by theoretical analysis and SVM classification,which selects the wavelet basis and scale based on multiple experiments.The proposed method is applied on the data set(1999 Golub used in ALL and AML).Five feature genes are extracted,whose classification test accuracy rate can reach 94.12%.It can be seen that the algorithm has high feasibility and effectiveness,and can provide some reference for the study of the differentially expressed genes between tumors.

Microarray data;wavelet modulus maxima;SVM

TP391.4

A

1008-6609(2016)05-0046-03

陈小梅，女，福建漳州人，硕士，助理实验师，研究方向：模式识别、图像处理。