完整建构学生知识体系 实现高效课堂
——“找次品”一课再思考
2016-02-06刘颖
刘颖
(安徽省淮南师范附属小学)
完整建构学生知识体系 实现高效课堂
——“找次品”一课再思考
刘颖
(安徽省淮南师范附属小学)
合理安排教学内容,深入领会教材的编排意图,引导学生经历知识的形成过程,探究规律产生的科学依据,寻找规律间的内在联系,完整建构学生知识体系,是实现高效课堂的重要环节。
完整建构;高效课堂;课堂回顾
在高效课堂的研讨活动中,本人执教了“找次品”一课,以“找次品”这一操作活动为载体,让学生通过观察、猜测、试验等方式感受解决问题策略的多样性,在此基础上,通过归纳、推理的方法体会运用优化策略解决问题的有效性,感受数学的魅力。以下摘录其中两个片段进行理性分析和反思。
【课堂回顾】
片段一:9个螺丝钉中找次品
1.第二次探究
师:如果在9个螺丝钉,有一袋稍轻,至少用天平称几次就能保证找到次品呢?
摆一摆、画一画,记录你称的过程。
集体交流:(课件出示)
生1:9→(1、1、1、1、1、1、1、1、1) 4次
生2:9→(4、4、1)→4(2、2)→2(1、1) 3次
生3:9→(4、4、1)→4(1、1、2)→2(1、1) 3次
生4:9→(2、2、2、2、1)→2(1、1) 3次
师:还有更少的吗?怎么称的?
生5:9→(3、3、3)→3(1、1、1) 至少2次
(相机完整表格一):
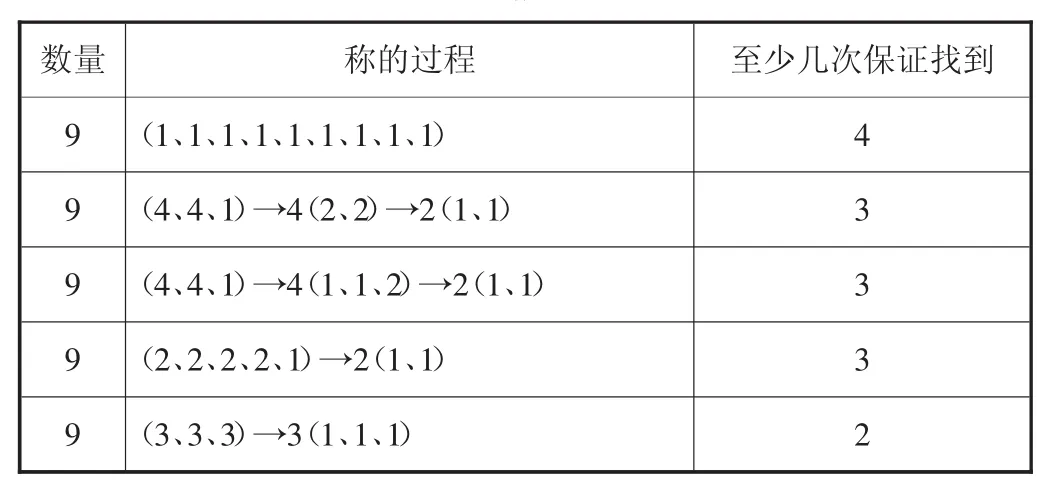
表格一
2.对比优化渗透三分法
思考:请仔细观察表格中的五种称法,2次的这种称法有什么特点呢?
引导发现:一开始就把9个螺丝钉平均分成3份。称1次,就可以判断次品在哪一份里。再把有次品的一份平均分成3份,就可以找到次品。
3.猜想,验证规律
师:“把总数一开始就平均分成3份,可以用最少的次数找到次品”。这个猜想对吗?
师:下面请同学们以6袋茶叶为例来验证。
交流:生1:6(2、2、2)→2(1、1) 至少2次保证找到。
生2:6(3、3)→3(1、1、1) 至少2次保证找到。
师:这两位同学都是至少2次保证找到,说明平均分成3份找次品的方法就是最少的方法。
片段二:“8个螺丝钉找次品”
师:同学们,通过刚才的活动我们可以得到:把总数一开始就平均分成3份,就可以用最少的次数找到次品。如果是8个螺丝钉中,有一袋稍轻,至少要称几次才能保证找到次品?请大家想想怎么称次数最少?
生动手操作(教师巡视指导)
交流填写表格二:

表格二
说一说:2次就找到次品的方法。
师:观察表格,组内说一说你的发现。
交流得出:把8袋茶叶分成3份,尽量均分3份。
(每次分的尽可能接近),就能保证至少2次找到。
【课堂行为分析】
《义务教育数学课程标准》指出:“有效的数学学习活动不能单纯地依赖模仿和记忆,动手实践、自主探索与合作交流是学生学习数学的重要方式。”着力让学生通过参与有效的实际操作、观察比较概括出“找次品”的最佳方案。在自主建构知识的基础上,建立了“猜想—验证—反思—运用”的教学模式。上完后,总觉得一节课被分成了两个孤立部分(待测的物品是“3的倍数的”和“不是3的倍数的”),这两部分能否和谐联结?基于以上思考,下面就从“完整知识建构”方面谈一谈。
本节课注重“数学化”的过程,即由具体到抽象,由特殊到一般的数学分析模式。先让学生探讨待测物品为2个螺丝钉、3个螺丝钉、5个螺丝钉、9个螺丝钉时怎样找次品,并罗列出各种解决方案,且各有侧重。如,2个待测物品引入用天平称的方法,借助肢体语言,认识天平的平衡原理;研究3个待测物品,通过摆一摆的方法,引导学生推理,体会“保证找到”的意义;研究5个待测物品,仅要求学生说出找次品的方法,不需要进行规律总结,让学生感受解决问题策略的多样性,并学会用数学的方法记录;研究9个待测物品,从这些方案中寻找规律,总结、提炼出一般方法和优化策略,使学生经历由多样化过渡到优化的思维过程。但由于本节课把2课时知识融在一课时进行,内容多,时间紧。有些知识点只是一带而过,不能进行深入探讨。如:“9个螺丝钉中找次品”得出均分3份,保证至少找到的原因,是“第一次尽可能多的排除。”并没有进一步深入探究排除了多少?其他方法第一次又能排除多少?学生的思维仅仅停留在这一层面。再如,在研究“8个螺丝钉中找次品”这一环节,就更为仓促,学生汇报完几种情况后,比较得出:“尽可能均分3份,保证至少找到。”
学生是否真正理解“均分3份和尽量均分3份的道理?为什么这样就能保证找到次品次数最少?两者之间是否有联系?”如何让学生知其然,知其所以然。因此在研讨的基础上增加了一个“深入理解”的环节,再次引导学生认真观察表格一和表格二,仔细比较称的过程,不难发现:3的倍数可以用3n来表示,不是3的倍数的就可以表示成3n+1或3n+2。从而推出:
当3n时:n n n→一次就能排出三分之二
当3n+1时:n n n+1→一次也能排出接近三分之二
当3n+2时:n+1 n+1 n→一次就能排出三分之二还多
使学生明白“均分三份”和“尽可能分成三份”,为的就是一次能尽可能多地排除,保证次数最少的道理,达到知识之间的和谐联结,完整建构学生的知识体系。
【总结归纳】
总之,合理安排教学内容,深入领会教材的编排意图,引导学生经历知识的形成过程,探究规律产生的科学依据,寻找规律间的内在联系,完整建构学生知识体系,是实现高效课堂的重要环节。
郑毓信.“找次品问题”与数学思维[J].小学数学:教学版,2011(17).
·编辑 薛直艳
