基于运动元素分解与综合的机构自由度拓扑分析
2016-02-05罗建国韩建友
罗建国,韩建友
(1. 华北科技学院 机电工程学院,北京 东燕郊 101601;2. 北京科技大学 机械工程学院,北京 100083)
基于运动元素分解与综合的机构自由度拓扑分析
罗建国1,韩建友2
(1. 华北科技学院 机电工程学院,北京 东燕郊 101601;2. 北京科技大学 机械工程学院,北京 100083)
在分析空间任意单一移动或转动关节在固定坐标系三维坐标轴上分解运动元素的基础上,并通过坐标齐次变换映射得到其在固定坐标系的等效空间运动元素,然后将各关节的等效运动元素再进行空间三维分解,得到对应支链的等效主移动、等效副移动、等效转动运动元素集合。通过构建与固定坐标系三维坐标轴一一对应的三条移动运动元素集合拓扑表示线,并在其右侧对应构建运动元素集合拓扑表示线,将支链上各关节的等效移动或转动元素集合通过水平区间线表示。针对串联、并联、混联机构的不同形式,本文利用运动元素拓扑表示线,对应给出不同的运算和分析方法,从而得到其自由度的构成和数目。
机构;运动元素;拓扑表示;自由度
0 引言
人类对机构的研究是认识自然、改造自然的过程,更是理论与实践结合助推人类发展的过程。Freudenstein和Dobrjanskyj[1]将图论引入机构学已有百年历史,用图论[2]表示运动链的拓扑结构可以实现空间到平面的转化,将复杂结构简单化、直观化。王晓慧等[3]引入拓扑学理论,定义了并联机构的拓扑空间,分析了并联机构的拓扑特征,研究了并联机构的拓扑变换方法。罗阳军等[4]提出以输出端位移最大化为目标、具有最小输入端性能约束的柔性机构拓扑优化数学模型。牛小铁等[5]采用一种新方法对柔顺机构拓扑图提取,得到CAD系统可以识别的参数化模型。同时,将拓扑图用矩阵例(已经有邻接矩阵、关联矩阵等成果)等[6]表示。通过借组数学工具实现机构的分析和处理,为机构型综合和创新设计提供了有效的手段。机构自由度的求解已经有150多年的历史,传统的Kutzbach-Grübler公式[7]对大多数的机构是适用的,随着机构学的不断发展,很多新机构和典型机构不符合上述公式[8],黄真教授提出基于约束螺旋来求解机构自由度[9]获得了成功,能够适用于已知的所有机构形式。然而,该方法只能对机构自由度进行抽象的分析,机构在空间坐标系中的要素构成、要素特点不能明确表示,且不能将三维空间的机构空间活动能力用平面集合的方式体现。本文提出一种新的基于运动元素分解与综合的平面三维拓扑运算与分析方法,它能够反映机构自由度在空间坐标系的要素构成及其具体特点,并能将三维空间的机构空间活动能力分解成一维集合表示,既可以对机构进行自由度构成进行一目了然的直观分析, 还可为机构工作空间、奇异的后续分析提供非常便捷的途径和依据,从而为机构学的理论研究与进步作出新的贡献。
1 运动元素空间等效映射
空间机构是由一个或多个运动支链组合而成,通过不同的组合形式得到多种结构形式的机构,如串联机构、并联机构、混联机构,无论是哪一种机构形式,其基本组成单元是关节。关节作为机构最基本的组元,其运动元素可以分解为平移运动元素和转动运动元素。在此基础上可以得到包含多个平移运动元素、多个转动运动元素叠加的组合形式。对机构进行自由度分析是在分析出各关节的运动能力的基础上,给出对应的综合方法和规则,最终得到机构自由度构成和数目的最终结果。
空间单一运动支链末端点在各关节活动坐标中具有确定运动表示,通过齐次坐标变换可以实现运动支链末端点在固定基础坐标系中的坐标变换,从而实现该点所代表的运动元素由空间活动坐标系到固定坐标系的运动映射,如图1 和式(1)所示。
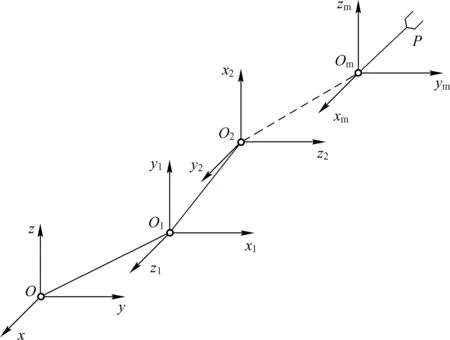
图1 运动元素齐次变换映射
(1)
空间任意线段在三维空间的等效映射结果仍然为线段或点,从而实现平移运动元素在三维固定坐标系的分解,即如图2和式(2)至(4)所示,对应线段所在的坐标区间为映射结果,即平移运动能力一维映射集合,它只包含坐标区间。空间任意圆可以看做某一转动关节绕确定轴线的转动运动元素,该圆向三维坐标的三个平面进行投影得到椭圆/圆/线段,而椭圆可以再次分解为四段圆弧的组合(如图3和式(5)至(6)所示),同时三平面内的椭圆/圆/线段在三坐标轴上还有对应的投影线段或点,从而实现空间任意转动运动元素在三维固定坐标系的分解,如图4和式(7)所示,对应平面内曲线(椭圆/圆)绕三维直角坐标的转动角度区间、对应平面内曲线(椭圆/圆)/线段/点在三维直角坐标系上的投影线段或点的坐标区间为映射结果,即平移运动能力一维映射集合,它既包含坐标区间,也包含角度区间。
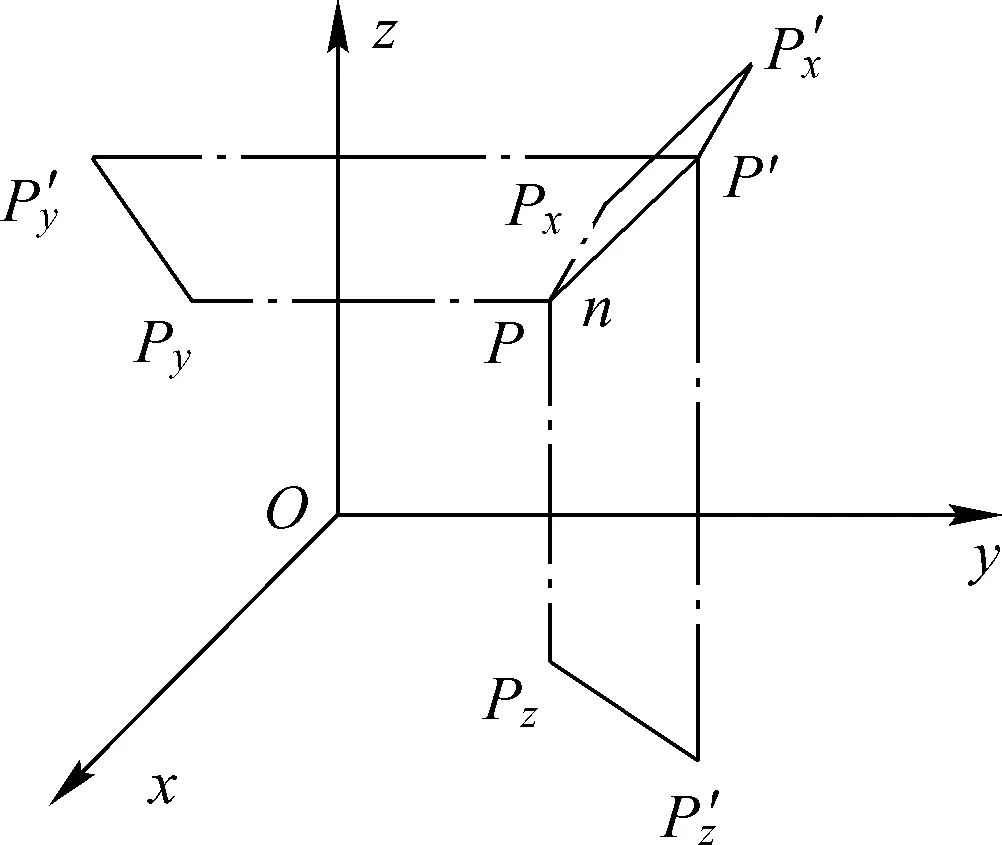
图2 平移运动映射

图3 椭圆运动分解映射

图4 转动运动映射
{Pn}→{Px∪Py∪Pz}main
(2)
(3)
(4)
{RO}e→{Rc1(∠a3c1a4)}c∪{Rc2(∠a1c2a2)}c∪
{Rb1(∠a2b1a3)}c∪{Rb2(∠a1b2a4)}c
(5)
{RO}e→{Rc1(α1)}c∪{Rc2(α2)}c∪
(Rb1(α3))c∪{Rb2(α4)}c
(6)
{Rn}→{Rx∪Ry∪Rz}∪{Px∪Py∪Pz}vice
(7)

在分析空间任意单一移动关节、单一转动关节基本运动元素的基础上,将其在固定坐标系三维坐标轴上的分解,利用空间支链上各关节特性通过坐标齐次变换映射,得到其在固定坐标系的等效空间运动元素,然后将各关节的等效运动元素进行空间三维分解,得到对应支链的等效主移动、等效副移动、等效转动运动元素集合,如图5所示。采用此方法可以将任意串联支链上的移动关节和转动关节的运动元素映射到固定坐标系,得到等效空间运动元素集合,如图6所示。
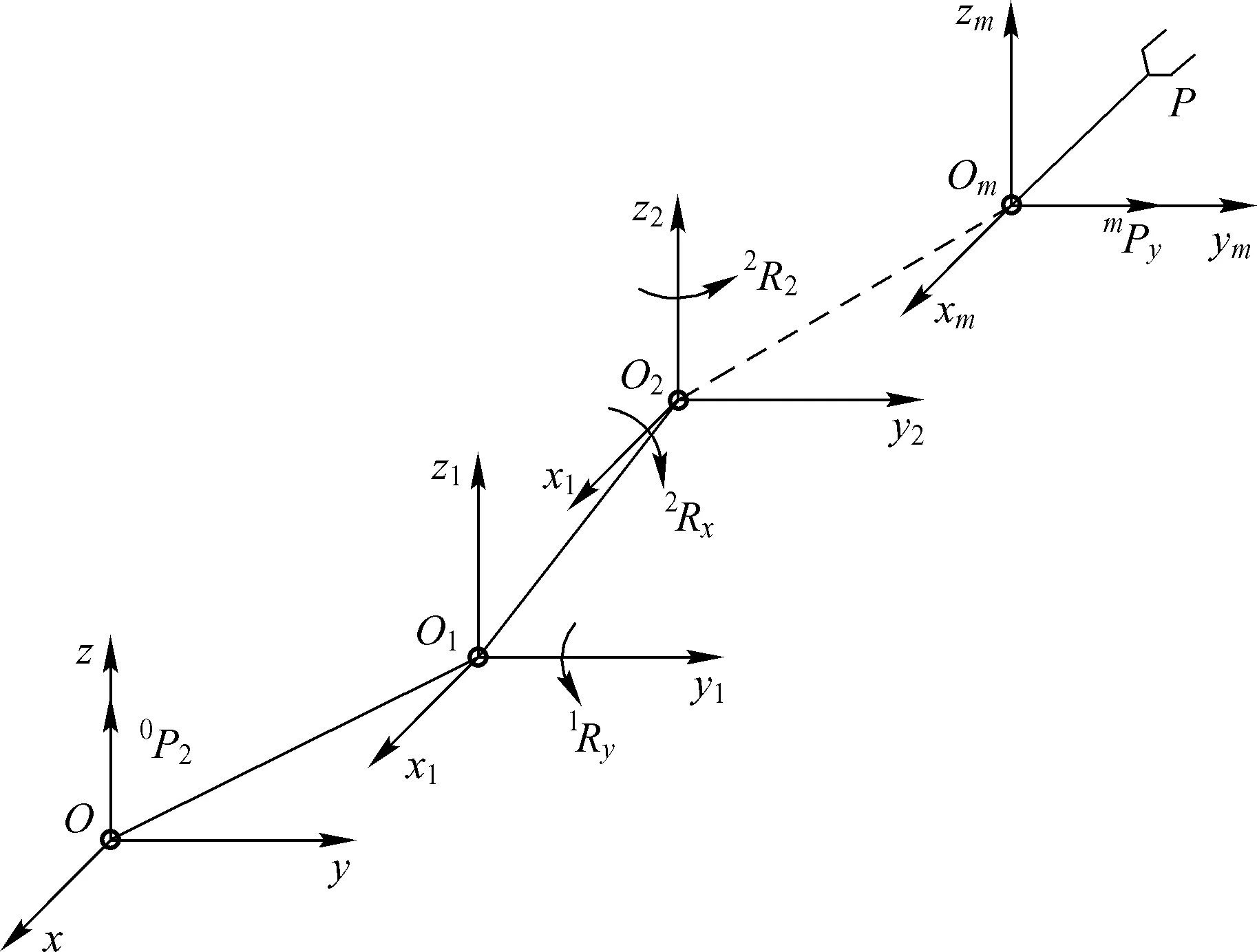
图5 串联支链运动元素
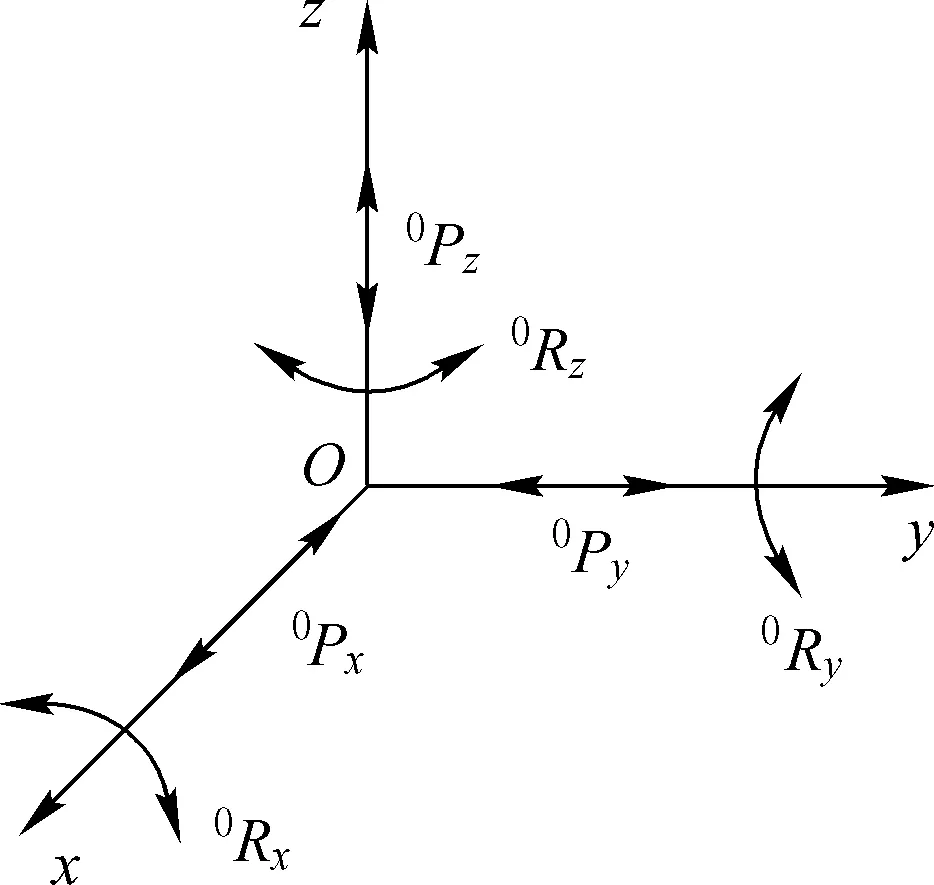
图6 图5中串联支链运动元素等效空间映射结果
(8)
{1Ry}→{0Ry}∪{0Px(1Ry)∪0Py(1Ry)∪0Pz(1Ry)}vice
(9)
{2Rx∪2Rz}→{0Rx∪0Rz}∪{0Px(2Rx)∪0Py(2Rx)∪0Pz(2Rx)}vice∪{0Px(2Rz)
∪0Py(2Rz)∪0Pz(2Rz)}vice
(10)
{mPy}→{0Py}
(11)
{0Pz}∪{1Ry}∪{2Rx∪2Rz}∪{mPy}→{0Pz}∪{0Ry}∪{0Px(1Ry)∪0Py(1Ry)∪0Pz(1Ry)}
∪{0Rx∪0Rz}+{0Px(2Rx)∪0Py(2Rx)∪0Pz(2Rx)}
∪{0Px(2Rz)∪0Py(2Rz)∪0Pz(2Rz)}∪{0Py}
={0Rx∪0Ry∪0Rz}∪{0Py∪0Pz}main∪{0Px∪0Py∪0Pz}vice
(12)
以图5所示串联支链为例,将各坐标系中的空间运动元素向固定坐标系进行映射变换,得到对应的等效运动元素集合,式(8)表示固定坐标系中平移运动元素0Pz的等效映射结果。式(9)表示绕坐标轴O1y1的转动运动元素1Ry在固定坐标系中的等效映射的结果,包括等效映射转动运动元素集合和等效映射副平移运动元素集合,0Px(1Ry)、0Py(1Ry)、0Pz(1Ry)分别表示转动运动元素1Ry在固定坐标系中沿着坐标轴x、y、z的等效映射分解副移动运动元素。同理,可以得到式(10)中所示活动坐标系O2x2y2z2中转动运动元素2Rx、2Ry在固定坐标系中的等效映射的结果,式(11)中活动坐标系Omxmymzm中平移运动元素mPy的等效映射结果。
综合式(8)至(11)的映射结果,可以得到图5所示串联支链中所有空间运动元素的等效映射结果,如式(12)所示,它包含了等效映射主平移运动元素集合{0Py∪0Pz}main、等效映射副平移运动元素集合{0Px∪0Py∪0Pz}vice、等效映射转动运动元素集合{0Rx∪0Ry∪0Rz}。
2 机构自由度拓扑分析
2.1 运动元素的拓扑表示
拓扑学主要研究拓扑空间在拓扑变换下的不变性质和不变量。图论是数学的一个分支,它以图为研究对象,研究顶点和边组成的图形的数学理论和方法,图论的研究对象相当于“一维的拓扑学”。基于拓扑学和图论的基本原理和方法,构建与固定坐标系三维坐标轴一一对应的三条平移运动元素集合拓扑表示线,将支链上各关节的等效映射主移动元素通过“低且细”的水平区间线表示,图中下标为区间坐标,如图7所示。在右侧构建与固定坐标系三维坐标轴一一对应的三条转动运动元素集合拓扑表示线,将支链上各关节的等效映射转动运动元素、等效映射副平移运动元素分别通过“低且细”、“高且粗”的水平区间线表示,图中下标为区间坐标,上标为转动中心点和半径,如图8所示。

图7 主平移运动元素拓扑表示
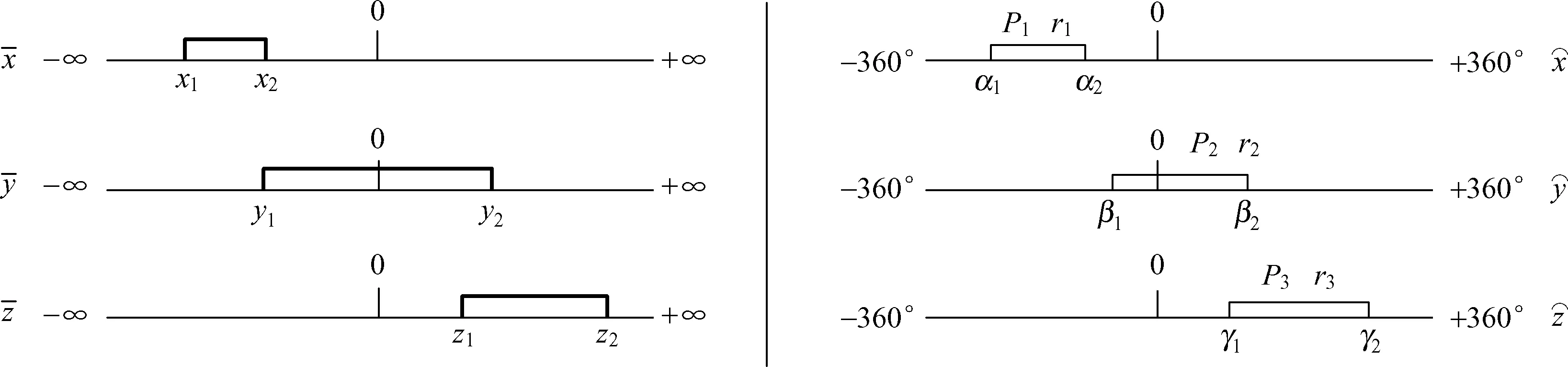
图8 转动运动元素、副平移运动元素拓扑表示
2.2 串联机构自由度拓扑分析
针对单一串联支链空间运动能力是各关节空间运动能力的叠加,即对六条运动元素集合拓扑表示线上的各区间进行并集运算,得到单一串联支链的空间运动元素拓扑综合分析结果,从六条运动元素集合拓扑表示线上可以非常直观看出拓扑线的数量,即为单一支链串联机构的自由度数,自由度的构成也一目了然。针对图5所示支链的等效映射运动元素集合分析结果,可以得知{0Rx∪0Ry∪0Rz}+{0Py∪0Pz}main为确定自由度(或主自由度),{0Px∪0Py∪0Pz}vice为不确定自由度(或伴随自由度),从而可以得知该机构具有5个确定自由度,当机构处于某些特殊情形时,即{0Px}vice≠Φ,不确定自由度可以为3,机构将有6个自由度,如图9所示。

图9 串联支链自由度拓扑分析
给出机构自由度的计算公式如下:
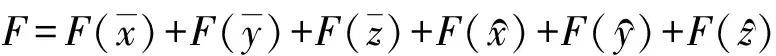
(13)
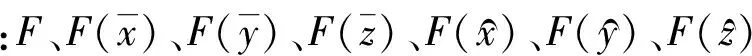
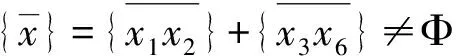



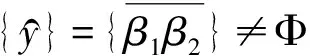
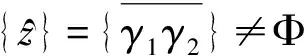
由图9可知,对应机构的自由度数目为:

=1+1+1+1+1+1=6
(14)
2.3 并联机构自由度拓扑分析
并联机构是由多条串联支链组合而成,将并联机构各串联支链的空间活动能力取交集,即可得到并联机构的空间活动能力,利用串联支链自由度数目和构成的分析结论,并联机构自由度数目可以由各串联支链的六条运动元素集合拓扑表示线进行交集运算得到。在此以一个三支链并联机构的自由度求解为例,各支链的自由度拓扑分析如图10、图11、图12所示,通过对同类运动元素拓扑表示线上区间的交集运算,得到并联机构的自由度拓扑分析结果,如图13所示。

图10 并联机构中第1条串联支链自由度拓扑分析
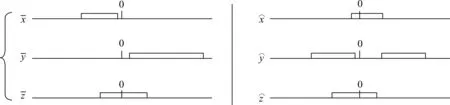
图11 并联机构中第2条串联支链自由度拓扑分析
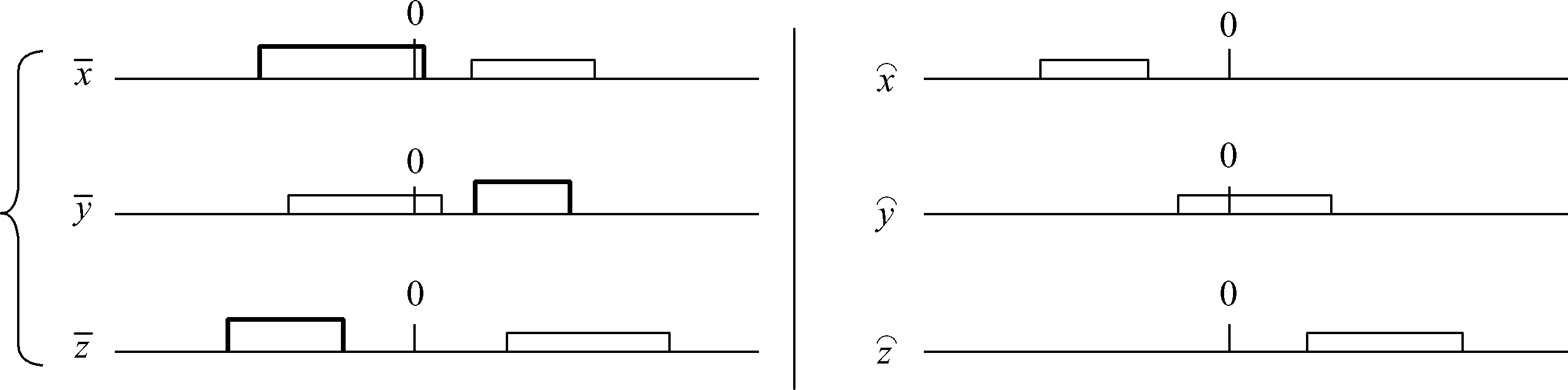
图12 并联机构中第3条串联支链自由度拓扑分析
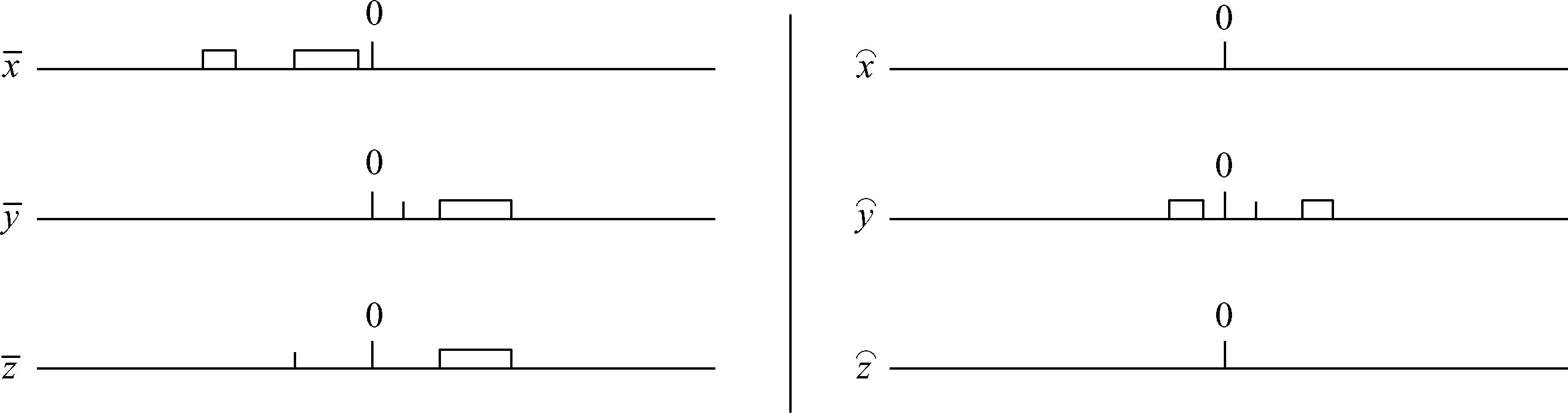
图13 并联机构自由度拓扑分析
由图13的分析结果可以得知该并联机构的自由度数目为:

=1+1+0+0+1+0=3
(14)
混联机构是由串联支链和并联机构组合而成,它可看成两个串联支链空间活动能力的并集,故混联机构的自由度数则按照并联机构六条运动元素集合拓扑表示线与串联关节或支链的六条运动元素集合拓扑表示线进行并集运算,从而得到其自由度的构成和数目,在此不再举例赘述。
3 结论
本文基于关节-支链-机构对基本运动元素等效映射分解与综合,利用拓扑分析理论,找出了可便捷地对机构自由度分析与计算的方法,具体结论如下:(1) 空间任意关节的运动元素可以通过齐次变换实现等效映射,平移运动元素唯一对应等效映射主平移运动元素集合,转动运动元素等效映射转动运动元素集合、等效映射副平移运动元素集合。
(2) 支链等效映射主平移运动元素集合、副平移运动元素集合、转动运动元素集合可以通过平面六维拓扑表示线的区间表示与运算实现其自由度数目与构成分析。
(3) 串联机构、并联机构、混联机构的自由度数目和构成,可以通过机构分支链自由度拓扑分析,得到其通用的分析方法,并得到其直观的分析结论。
通过本项目的研究,不仅能丰富和完善现有机构学研究理论和方法,为机构自由度分析提供普适、直观的科学理论和方法;同时,还可基于该理论和方法、有关的数学模型对工程实际领域的新机构的实际应用,起到很好的推动作用。
[1] Freudenstein F, Dobrjanskyj L. On a theory of type synthesis of mechanisms. In: Proceedings of 11th International Congress of Applied Mechanics. Berlin: Springer, 1964:420-428.
[2] 卢开澄. 图论及其应用[M]. 北京:清华大学出版社,1984,3-20.
[3] 王晓慧,张建军,范顺成,张顺心. 基于拓扑特征的并联机构拓扑变换[J]. 机械科学与技术,2005,24(11):1310-1312.
[4] 罗阳军,亢战,吴子燕. 考虑不确定性的柔性机构拓扑优化设计[J]. 机械工程学报,2011,47(01):1-7.
[5] 牛小铁,李兆坤,张宪民,等. 柔顺机构拓扑图提取[J]. 机械设计与研究,2013,29(01):18-21.
[6] Suh C H, Radcliffe C W. Kinematics and Mechanisms Design. New York: John Wiley&Sons, Inc.1978(chapter 5).
[7] Sandor G N, Erdman A G. Advance Mechanism: Analysis and Synthesis. Prentice Hall, Englewood Cliffs,NJ, 1984(chapter 6).
[8] 黄真, 赵永生, 赵铁石. 高等空间机构学[M]. 北京:高等教育出版社, 2006,115-135.
[9] 黄真,刘婧芳,李艳文. 150年机构自由度的通用公式问题[J]. 燕山大学学报,2011,35(01):1-14.
Topological Analysis of Degree of Freedom of Mechansim Based on Decomposition and Synthesis of Moving Element
LUO Jian-guo1, HAN Jian-you2
(1.SchoolofMechanical&ElectricalEngineering,NorthChinaInstituteofScienceandTechnology,Yanjiao, 101601,China;
2.SchoolofMechanicalEngineering,BeijingUniversityofScience&Technology,Beijing, 100083,China)
Based on the analysis of sub moving elements in fixed coordinate system from pure translation and pure rotation moving elements, the equivalent space motion element is obtained by means of coordinate transformation, three dimensional decomposition dealt with each joints, equivalent main moving element set and equivalent vice moving element set and equivalent rotation moving element obtained then. Three topological line on the left side is adopted to express the corresponding translation moving element set on three dimensional coordinate axis respectively, another three topological line on the right side is adopted to express the corresponding rotation moving element set on three dimensional coordinate axis respectively, horizontal line with different height and thickness used to display the section, different computation and analysis methods provided to find the construction and number of degree of freedom of serial mechanism and parallel mechanism and hybrid mechanism.
Mechanism;Moving element;Topological expression;Degree of freedom
2016-02-17
河北省高等学校科学技术研究资助项目(Z2015072),中央高校基本科研业务费资助项目(3142015023),国家自然科学基金资助项目(50975024)
罗建国(1977-),男,湖南岳阳人,博士后,华北科技学院机电工程学院副教授,E-mail:luojg_1598@163.com
TH112
A
1672-7169(2016)02-0068-06
