三角形全等的解题策略分析

黄国强

摘 要：在初中数学学习过程中，几何知识学习是其中较难的学习部分，而作为几何学习的基础，三角形全等这一问题的学习掌握更是重中之重，所以应该给予其更多的时间与精力。对三角形全等解题策略进行详细分析，进一步分析了当前初中生对几何知识学习方面的具体情况并掌握的相关问题所在，提出具体化的解题策略，力求能够帮助学生更好地对三角形全等问题进行解答。

关键词：三角形全等；解题策略；逆向思维

在初中数学的几何图形学习过程中，对三角形关系证明等问题十分常见，而在该部分的学习过程中，最为重要的就是三角形全等这一课题的探讨，通常该部分问题就是探究两个三角形之间的边角关系。同时，在对该类三角形的几何问题进行解决的过程中往往使用最多的就是三角形全等理论，然后以此为基础对相关结论或问题进行证明与解决。所以，就三角形的几何题目解题方面而言，三角形全等是其中最基础的一个部分，也是不可或缺的一个部分，笔者通过详细分析初中八年级的三角形全等问题，对其相关方面进行了解。

一、我国初中几何具体的教学现状

在初中数学知识的学习过程中，全等三角形作为其中一个非常重要的学习内容，《义务教育数学课程标准》规定：通过该部分知识的学习，全面发展学生数学课程时所具备空间思维、几何直观以及推理等相关能力，同时是对数学课程达成四大目标的一个重要理论基础。

以当前我国在几何教学方面的相关内容为基础可以了解到，在对该方面问题进行解答时，往往通过证明这一方式，并以此为基础对学生逻辑思维方面的能力进行培养。但是由于该方面知识所具备的特征：学习难度较大，在日常生活中使用情况也非常少，同时伴随这其自身相关原理与本质方面内容的理解较为困难等问题，所以使得初中生在具体学习过程中对该部分的兴趣较为薄弱，甚至达到了厌学的程度。随之而来的就是该方面数学学习信心的缺失，不过其中一部分学生则因为其所具备的挑战性强化了好奇心，进一步增加了对该方面学习的兴趣。时间一长，几何学习就成为初二学生的一个数学学习的分水岭。三角形全等知识作为几何知识的基础，为了更好地解决上述问题，教师要有针对性地对该部分进行教学，尽力满足不同类型学生对该部分知识学习的相关问题。

二、采取逆思维方式，证明全等三角形的解题策略

在进行三角形线段、角等方面的相等问题的证明过程中，往往就是要对两个三角形的全等关系进行证明，所以，在具体解题的过程中，可以采取逆向的思维逻辑方式，换句话说，若是要求两个三角形是全等关系就必须满足哪几个条件？理论上来讲就是要满足“边角边、角角边、角边角”三个中的一种，所以就要以此为基础，针对性地寻找满足条件，看题、看图，思考同时进行，在数形结合的基础上，真正意义上将题目情况掌握，然后将其解决。同时，可以根据题目自身所提供的相关条件，了解某些有关信息，之后根据AAS/SAS/SSS/ASA/HL等相关等式关系对三角形全等关系进行证明。譬如，若知道三角形的两边相等，就可以针对性地证明其夹角是相同的（SAS），同时若第三条边也获得相等的结果（SSS），或者是知道某一组等角后，又证明其对边相等（AAS）。因此，在具体解题过程中，可以根据题目所给信息，进行三角形全等条件的套入，最终根据具体符合的条件理论基础实现三角形全等问题的证明。

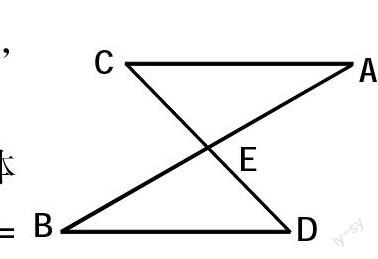
例题：如图所示三角形，其中AC=BD，∠C=∠D；问题：CE=DE？进行详细解释。

分析：该题目在思考过程中可以具体使用逆向思维方式，若图中AC=BD，∠C=∠D，CE=DE，就可以直接表明△ACE≌△BDE，所以，反过来想，只要证明了△ACE≌△BDE，那么CE=DE就顺理成章了。

解析：通过题目中给予的条件AC=BD，∠C=∠D，同时还有∠CEA=∠DEB三个条件，就可以证明△ACE≌△BDE（AAS），根据等边三角形的对边相等可以得到CE=DE。

点评：初中生在进行三角形几何问题角与边关系证明的过程中，首先可以以正常思维对该问题进行解答，试试看能否将问题解决，譬如该题，通过题目所出信息AC=BD，∠C=∠D这两个条件并不能直接获得CE=DE这一结论，那么就可以逆向思考问题，若我们将CE=DE这一结论当作是成立的，同时根据题目中所给予的条件AC=BD，∠C=∠D可以获得怎样的结论？而结合该部分内容，上述条件满足两个三角形全等条件中的“角角边”，所以可以证明两个三角形为全等三角形，即△ACE≌△BDE（AAS），所以最终就直接证明了CE=DE，因为全等三角形满足对边相等与对角相等的条件。

综上所述，在进行三角形几何题目的解题过程中，可以采取逆向的思维逻辑方式对全等三角形问题进行解决，同时该方式也是对该类习题进行解答的重要策略，并且通过实践性的解题经过，对相关几何问题的实际情况进行仔细分析之后，得出相应的高效性解题策略，并对解题过程进行总结，最终真正意义上对该类问题的解題方式进行掌握。

参考文献：

[1]王炳忠.浅谈探索性数学试题及解题策略[J].咸阳师范专科学校学报，2014（06）：18-20.

[2]范永祥.高中数学解题策略教学探究[J].文理导航：中旬，2013（13）：09-16.

编辑 谢尾合