高压高效三相异步电动机空载附加损耗分析与计算

王殿友

(佳木斯电机股份有限公司，黑龙江佳木斯154002)



高压高效三相异步电动机空载附加损耗分析与计算

王殿友

(佳木斯电机股份有限公司，黑龙江佳木斯154002)

摘要对高压高效三相异步电动机空载附加损耗产生的原因以及计算方法进行分析。并以一台1000kW电动机为例，建立求解高压高效三相异步电动机的二维瞬态场有限元模型，准确计算了电动机空载运行时的气隙磁密。 在二维瞬态场计算结果的基础上，计算电机空载运行状况下的附加损耗。最后通过铁耗分离试验得到电机空载附加损耗的试验值，并与计算值进行对比分析，验证了该计算方法的准确性。

关键词三相异步电动机；附加损耗；有限元

0引言

电动机作为耗电产品广泛应用于工业、商业、公共设施、家用等各个领域。电动机中用量较大的是三相异步电动机，因此提高异步电机效率水平，对降低电能消耗、节省能源等方面的研究有着重大意义。GB 30254—2013《高压三相笼型异步电动机能效限定值及能效等级》的发布实施以及“惠民工程”的提出，标志着高效节能电机将是今后电机研制的一个主要方向。

空载附加损耗的高低对电动机的效率及温升影响很大，因此准确计算电机中的空载附加损耗一直是高效电机设计的研究方向。传统的电机设计理论对附加损耗的计算是很粗略的，利用了大量的经验系数，导致理论计算与试验得出的数据误差较大[1]，从而导致某些型号电动机效率的设计值与试验值具有较大的误差。因此，深入分析空载附加损耗的计算方法是很有必要的。

采用数值法可以充分考虑电机铁心结构的变化、气隙磁场的高次谐波、磁路饱和等[2]，因此本文以一台1000kW电动机为研究对象，建立了发电机的二维有限元模型，分析了电动机空载运行时的磁场分布情况，计算了电动机的空载附加损耗，并与试验值对比，验证了计算方法的准确性，对高压高效电动机的电磁设计具有重要意义。

1空载附加损耗

三相异步电动机空载时铁心中的附加损耗主要是指铁心表面损耗和齿中脉振损耗，它是由气隙中的谐波磁场引起的。谐波磁场的形成主要是由于电机铁心开槽引起气隙磁导不均匀。

1.1　铁心表面损耗

电动机空载运行过程中，当谐波磁场相对与铁心表面发生相对运动时，就在铁心硅钢片的表面层附近产生涡流损耗和磁滞损耗。由于这种损耗主要集中于表面一薄层内，故称为铁心表面损耗。

1.2　齿中脉振损耗

因为定子和转子开槽，齿中的磁感应就取决于各个定子和转子齿的相互位置。如果一个定子齿正好对着一个转子齿，则气隙中的磁感应就是最大值；反之，如果一个定子齿正好对着一个转子槽，气隙的磁感应就是一个最小值，如图1所示。

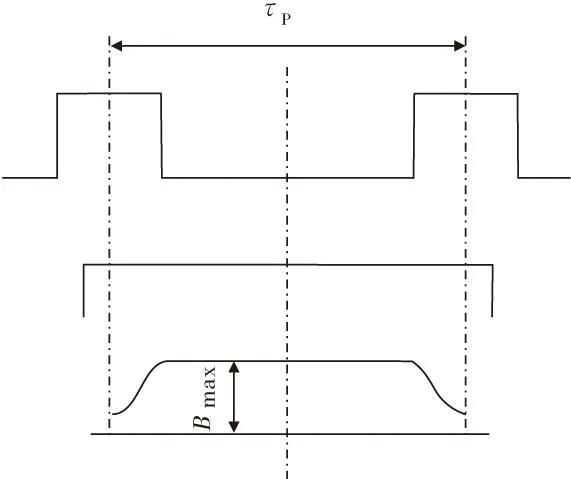
(a)定子齿与转子齿相对示意图

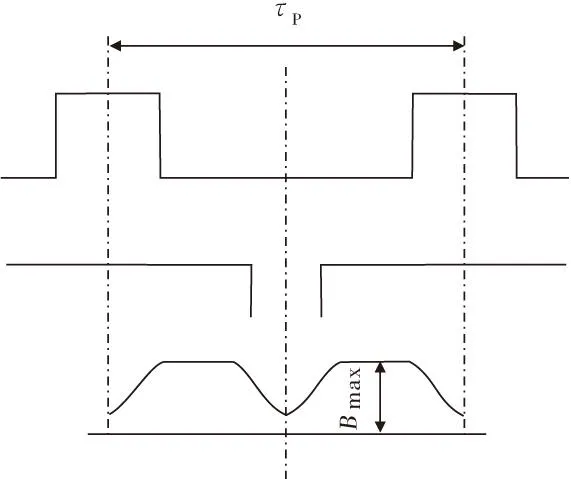
(b)定子齿与转子槽示意图

如果转子相对定子转动，由于磁导的周期性变化，一个槽距上的磁通也发生周期性的变化。因而通过定子齿的磁通就在它的最大值和最小值之间脉振，这样铁心中就出现附加的涡流损耗，这些损耗称为脉振损耗。对于转子来说，也可做相似的考虑[3]。

2模型与边值问题

本文所研究的三相异步电动机，基本参数见表1。

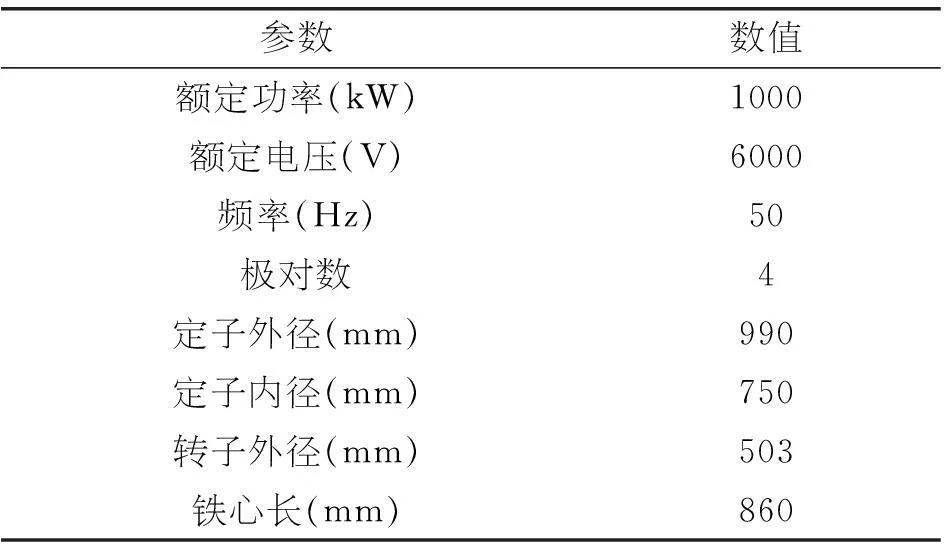
表1　电动机基本参数

对磁场进行有限元分析的基本假设如下[2]：

(1)磁场沿电机轴向不变，把问题作为二维磁场来处理；

(2)忽略定子绕组中涡流引起的集肤效应，认为电密在定子绕组截面上保持均匀；

(3)忽略温度对电导率的影响，假定计算温度为 75℃；

(4)忽略电网中的谐波含量，认为激励为正弦函数。

本文所选样机的二维有限元模型见图2，在给定的求解区域内，用向量磁位对数学模型进行表述。根据假设，只有分量，即，则满足的二维非线性恒定磁场的边值条件为

(1)

式中，Js—电流密度的轴向分量；μ—磁导率；S—二维有限元模型的外边界。

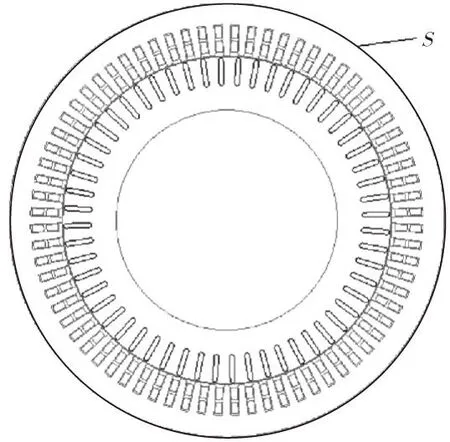
图2　电动机二维有限元模型

3空载附加损耗的分析与计算

3.1　空载磁场分析

利用有限元法计算空载附加损耗首先需要进行二维瞬态场计算，根据二维瞬态场有限元数学模型，计算电机空载磁场，电动机空载运行至1.64s时已经达到稳定状态，该时刻电动机的磁场分布如图3所示。

(a)磁力线分布图

(b)磁密分布图

电机空载运行稳定后，提取其一对极下的气隙磁密，并对其进行傅里叶分解，气隙磁密及谐波分析如图4所示。从图4中可以看出，电动机空载运行时，其一对极下得气隙磁密分布均匀对称。

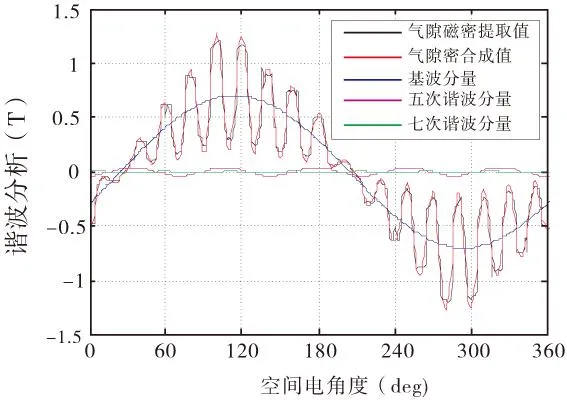
(a)气隙磁密

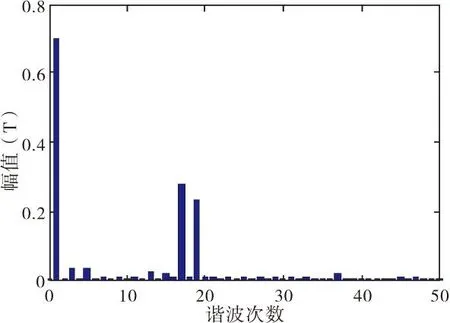
(b)谐波幅值

气隙磁密的各次谐波分量的幅值见表2。从表2中可以看出，在各次谐波中17次和19次谐波幅值相对于其它次谐波来说要大很多，分别占基波含量的 1/3左右，根据样机的结构参数可以确定，17次和19次谐波为该样机的一阶齿谐波，齿谐波分量与电动机定、转子槽配合及定、转子槽形尺寸关系密切[4]。齿谐波是引起电机空载表面附加损耗的主要原因，因此该分析结果为电机空载表面附加损耗的准确计算奠定了基础。

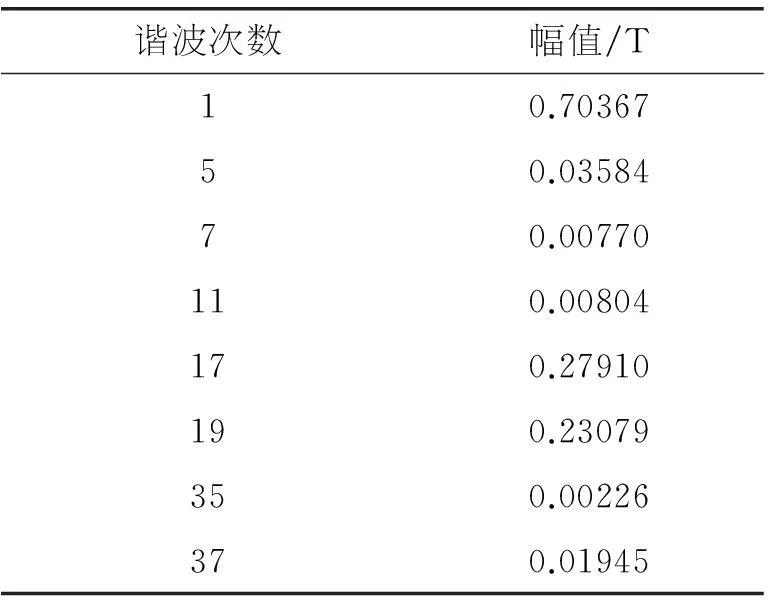
表2　气隙磁密谐波分量幅值

3.2　空载表面附加损耗的分析与计算

在异步电动机中，定子和转子铁心均由硅钢片叠压而成，而且定子和转子都槽。定子开槽引起的气隙磁导齿谐波磁场会在转子表面产生表面损耗，反之也是。转子表面损耗为[5]

(2)

式中，t2、b02—转子齿距和转子槽口宽；D2、lt2′—转子铁心外径和铁心长度；转子表面单位面积上的损耗为PA2=0.5k0(Z1n)1.5(B01t1)2；B01—谐波幅值。

根据上式及3.1节中得到的气隙磁密谐波幅值计算得到的电动机空载转子表面附加损耗如表3所示。

表3　空载转子表面附加损耗

从表3中可以看出，电动机空载运行时，表面附加损耗主要是由一阶齿谐波磁场引起的，高阶齿谐波引起的表面附加损耗数值非常小。因此在计算异步电动机空载表面附加损耗时，高阶齿谐波的影响可以忽略不计。

3.3　空载脉振损耗的分析与计算

在电动机二维瞬态场计算的基础上，对于定子齿部某剖分单元e而言，脉振损耗为

(3)

式中，k—损耗增加系数；σe—铁心材料涡流损耗系数；Bp1—齿中磁通密度脉振振幅。

因此，定子齿部脉振损耗为

(4)

将式(2)和式(4)中各符号的下标1及2相互对换，就可以得到定子表面损耗和转子齿脉振损耗的计算公式。

根据以上公式及二维瞬态场的计算得到电动机的空载附加损耗计算结果，见表4。可以看出，样机空载附加损耗为10067.05W；在空载附加损耗的计算结果中，定子表面损耗和定子脉振损耗数值相对较小，在工程近似计算中可忽略这两项的数值，减少了计算时间，缩短了产品的开发周期。

表4　空载附加损耗计算结果

4空载附加损耗试验结果对比分析

异步电动机空载运行时，输入功率消耗在定子铜耗、铁耗、机械耗和空载附加损耗上(转子电流很小，转子铜耗忽略不计)，其中定子铜耗及机械耗的测量比较容易，难点在于铁耗及附加损耗的分离。

将铁耗与空载附加损耗分离需用另一台辅助电机把被测电机的转子拖到同步转速ns进行试验。此时n= ns，s=0，I2=0，转子的机械损耗和空载附加损耗全由辅助电动机供给，定子电流纯为激磁电流。所以把此时定子输入功率减去此时的定子铜耗便得到基本铁耗，再将空载试验测量出的铁耗与空载附加损耗之和，将基本铁耗去除，则得到该电机的空载附加损耗[6]。

表5中给出了几个规格电动机空载附加损耗的计算值(有限元法)和试验值的对比。从表中数据可以看出，除了个别规格外，计算值与试验值的误差并不是太大，基本都在10%以内，对比结果可以验证本文附加损耗计算方法的准确性。

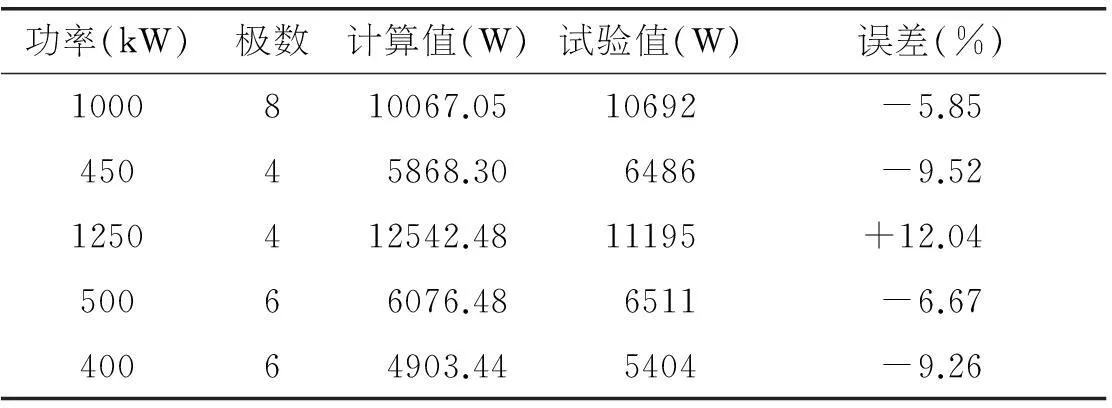
表5　空载附加损耗计算与试验结果对比

5结语

本文以一台1000kW电动机为研究对象，计算了电动机空载运行时的表面附加损耗和齿部脉振损耗，并将计算值与试验值进行对比分析，得出以下结论。

(1)表面附加损耗主要是由一阶齿谐波磁场引起的，高阶齿谐波引起的表面附加损耗数值非常小。因此在计算异步电动机空载表面附加损耗时，高阶齿谐波的影响可以忽略不计；

(2)定子表面损耗和定子脉振损耗数值相对较小，在工程近似计算中可忽略这两项的数值，减少了计算时间，缩短了产品的开发周期；

(3)根据空载附加损耗的计算值与试验值对比结果，能够验证计算方法的准确性，对高压高效异步电动机的电磁设计具有一定的指导意义。

参考文献

[1]杨枢林，段淑贞，秦斌．三相异步电动机中的槽形对空载附加损耗的影响[J]．机械管理开发，2007，(1)：1-2．

[2]汤蕴璆，梁艳萍．电机电磁场的分析与计算[M]．北京：机械工业出版社，2010．

[3]B.海勒尔，V.哈马塔．异步电动机中谐波磁场的作用[M]．北京：机械工业出版社,1980．

[4]左涛．异步电动机定、转子槽配合对附加损耗的影响[J]．防爆电机，2006，41(6)：46-47．

[5]陈世坤．电机设计[M]．北京：机械工业出版社，2000．

[6]许实章．电机学[M]．北京：机械工业出版社，1992．

Analysis and Calculation on Noload Additional Loss of

High-Voltage High-Efficiency Three-Phase Induction Motor

WangDianyou

(Jiamusi Electric Machine Co.,Ltd.,Jiamusi 154002, China)

AbstractThe cause and calculation method on additional loss of high-voltage high-efficiency three-phase induction motor at noload were analyzed. Taking a 1000kW motor as an example, a finite-element model for solving 2-D transient field of the motor was established and air-gap flux density distribution of the motor at noload was accurately calculated. The additional loss of the motor under noload running state was calculated based on calculation result of 2-D transient field. Finally, the experimental result of additional loss of the motor at noload was obtained by iron loss separation test. By comparing experimental result with calculation result, accuracy of the calculation method was verified.

Key wordsThree-phase induction motor；additional loss；finite element

收稿日期：2015-08-20

作者简介：王殿友男1971年生；毕业于哈尔滨理工大学电气工程专业，硕士研究生，现从事电机设计研发工作.

中图分类号：TM306

文献标识码：A

文章编号：1008-7281(2015)06-0027-004

DOI:10.3969/J.ISSN.1008-7281.2015.06.09