C4ISR系统指挥控制关系适应性演化模型和方法研究

张杰勇, 蓝羽石, 易　侃, 毛少杰, 王　珩

(1. 中国电子科技集团公司第二十八研究所信息系统工程重点实验室, 江苏 南京 210007;

2. 空军工程大学信息与导航学院, 陕西 西安 710077)



C4ISR系统指挥控制关系适应性演化模型和方法研究

张杰勇1,2, 蓝羽石1, 易侃1, 毛少杰1, 王珩1

(1. 中国电子科技集团公司第二十八研究所信息系统工程重点实验室, 江苏 南京 210007;

2. 空军工程大学信息与导航学院, 陕西 西安 710077)

摘要：研究了C4ISR系统结构中指挥控制关系的适应性演化问题。构建了C4ISR系统结构中的指挥控制关系模型,在对指挥控制关系适应性演化过程分析和描述的基础上,设计了演化过程中的指挥控制关系的结构变化代价和性能代价,并以最小化总的演化代价为目标函数构建了指挥控制关系适应性演化问题的数学模型。提出了基于n-Best策略层级聚类方法和遗传算法(genetic algorithm, GA)的问题模型求解思路。n-Best策略层级聚类方法用来获取每个任务阶段可行的指挥控制关系集合,而GA用来搜索最优的演化路径。最后通过某一仿真算例验证了求解方法的可行性、稳定性。

关键词：C4ISR系统; 指挥控制关系; 适应性演化; n-Best策略; 层次聚类方法; 遗传算法

0引言

C4ISR (command,control,communication,computing,intelligence,surveillance,reconnaissance)系统是集指挥控制、预警探测、情报侦察、通信、电子对抗和其他作战信息保障等功能为一体,用于军事信息的获取、处理、传递、决策支持和对部队实施指挥与控制以及战场管理的军事信息系统[1]。网络中心化条件下的C4ISR系统是一个典型的开放复杂系统,具备“即插即用,柔性重组、协同运行、按需服务”等新的能力[2]。其中,“柔性重组”是指在激烈的对抗环境下,系统结构能够根据系统外部环境和内部要素的变化,对自身的系统结构进行不断的适应性调整,以适应这种变化,从而始终保持系统整体的功能和性能。网络中心化C4ISR系统的这种“柔性重组”能力在对抗环境下可以表现为系统结构的“适应性演化”行为。虽然,“柔性重组”、“适应性演化”等概念提出来已经多年了,但是公开的资料文献中有关这些概念深入的研究和探索较少。其中,C4ISR系统单元之间的指挥控制关系作为其系统结构的重要组成部分,在实际的作战过程中,它也应该具有“柔性重组”能力,即具备“适应性演化”的行为。本文主要对C4ISR系统结构指挥控制关系的“适应性演化”过程和行为进行研究,构建指挥控制关系适应性演化问题的数学模型,并依据模型设计相应的求解方法。

1C4ISR系统结构指挥控制关系模型

C4ISR系统结构的系统单元划分方法有很多,一般根据不同的研究对象和问题的需要,可以有不同的划分方法。其中,比较常见的一种划分方法是将系统结构的系统单元划分为4类[3]:情报获取单元(observe,O)、情报处理单元(process,P)、决策控制单元(decide,D)和响应执行单元(act,A),其他的方法基本就是这4种方法的简单变型,比如:将P和D合并为一类,称为指挥控制单元[4],系统基本单元中不包含A[5]等。

由于本文的研究对象为C4ISR系统结构的指挥控制关系,因此,只将C4ISR系统结构的系统单元划分为两大类:指挥控制单元类和被指挥控制单元类。

定义 1指挥控制单元,即决策资源,是信息处理并进行决策的单元,是C4ISR系统资源的指挥者,主要功能是信息处理并进行指挥决策。设C4ISR系统结构所拥有的指挥控制单元数量为K,那么整个指挥控制单元集合为:D={D1,D2,…,DK}。

定义 2被指挥控制单元,即各类作战平台,包括各类探测单元和火力单元,是具有某种完成任务能力的独立实体,它受指挥控制单元指挥来执行任务,是指挥控制单元执行任务的凭借。设C4ISR系统结构所拥有的被指挥控制单元的数量为N,那么整个被指挥控制单元集合为:P={P1,P2,…, PN}。

同时,只考虑两类C4ISR系统结构的指挥控制关系:一是指挥控制单元与被指挥控制单元之间的指挥控制关系；

二是指挥控制单元之间的协作关系。

由以上定义和描述可得,一个简单的C4ISR系统结构指挥控制关系模型如图1所示。由图1可知,为了避免决策冲突和混乱,每一个被指挥控制单元在同一时刻只能受一个指挥控制单元的指挥。

图1　C4ISR系统结构的指挥控制关系模型

2指挥控制关系适应性演化问题建模

2.1问题的基本描述

C4ISR系统结构指挥控制关系适应性演化的输入条件是作战任务的分配方案,即被指挥控制单元与作战任务之间的分配方案,该方案可以用甘特图来表示[6]。指挥控制关系的适应性演化是指随着时间的推进,由于不同的时间阶段执行不同的作战任务分配方案,使得底层的被指挥控制单元之间的协作关系不断发生变化,通过对上层指挥控制关系模式的适当调整,可以达到上层指挥控制关系适应底层被指挥控制单元间在执行作战任务上协作关系的变化。指挥控制关系适应性演化的目标是通过对上层指挥控制关系的适当改变,使得系统能够在底层任务分配关系不断发生变化的情况下,仍就可以保持很高的任务完成效率,包括信息处理效率和指挥决策效率。

指挥控制关系模式随任务分配方案的执行而适应性演化的简单描述如图2所示,图中Gi(i=1,2,3,…)表示第i个任务阶段所采用的指挥控制关系模式。

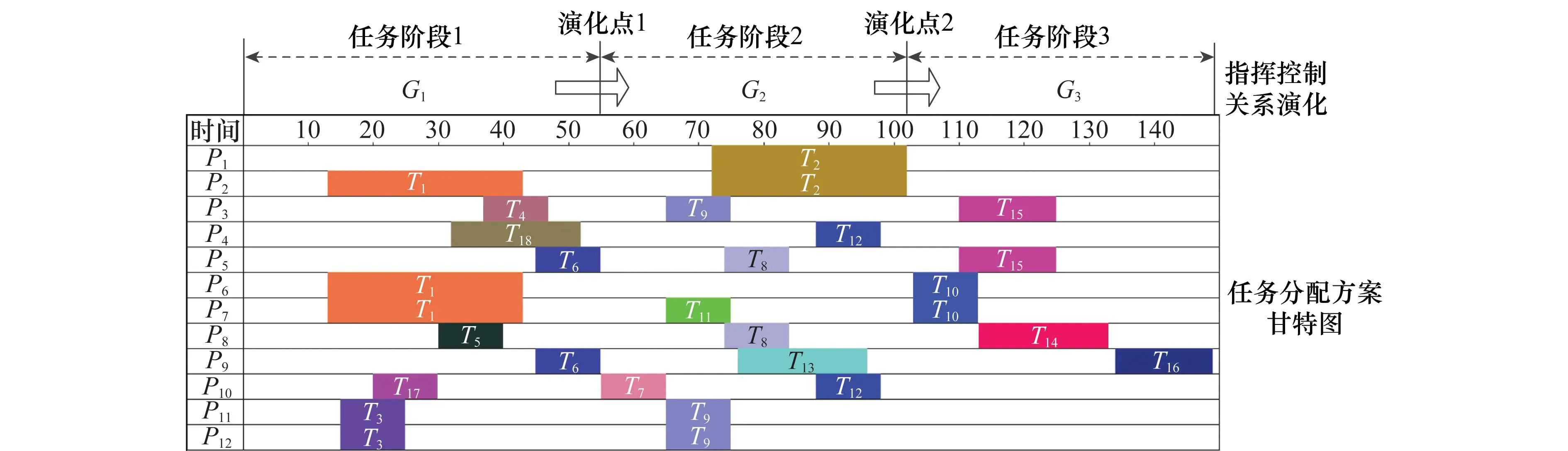
图2　C4ISR系统结构的指挥控制关系演化过程

由图2可知,每个任务阶段的不同任务分配关系对应不同的指挥控制关系模式,假设某一次作战过程具有L个任务阶段(如:在图2中,L=3),相邻的任务阶段之间由演化时间点分隔(如:在图2中,演化时间点的数量为2),通常一次作战过程的指挥控制关系演化的时间点的设置是由军事领域专家结合某一具体战役使命的特点给出。记第i(i=1,2,…,L)个任务阶段的任务分配方案为Si(i=1,2,…,L),这样,整个任务分配方案S可以用每个任务阶段的任务分配方案的序列来表示,即S=S1→S2→…→SL。

而指挥控制关系的适应性演化过程就是执行不同任务阶段的任务分配方案为Si(i=1, 2,…,L)的指挥控制关系模式Gi(i=1,2,…,L)的不断变化过程。这样,C4ISR系统指挥控制关系的适应性演化过程可以描述为这样一个多阶段的决策问题。对于这个多阶段决策问题中每个阶段的任务分配方案,都可以对应着许多个可行的指挥控制关系的结构模式,相邻阶段的不同指挥控制关系结构模式之间存在单向的连接关系,表示上一阶段的指挥控制关系的结构模式经过变换后可以转变为下一阶段的指挥控制关系的结构模式。

从一种指挥控制关系模式G1演化为另一种指挥控制关系模式G2,这种关系模式的演化会带来结构变化的代价,同时,也会带来指挥控制关系模式G2执行该任务阶段的任务分配方案的性能变化,本文将这种性能的变化称为性能代价,而整个指挥控制关系的适应性演化过程就是结构变化代价和性能代价之间的权衡折中。

2.2结构变化代价

这里的结构变化代价包括指挥控制单元与被指挥控制单元之间的指挥控制关系的变化代价和指挥控制单元之间的协作关系变化的代价。

假设在两个指挥控制关系模式G1、G2中,增加或减少一个指挥控制单元的被指挥控制单元,产生的代价为WA;在指挥控制单元之间协作关系中,增加或删除一条指挥控制单元之间的连接,变化的代价为WC。那么指挥控制关系模式G1与G2之间结构变化的代价为

(1)式中,N为被指挥控制单元的数目；K为指挥控制单元的数目；R(G1,G2)为指挥控制关系模式G1和指挥控制关系模式G2中指挥控制单元与被指挥控制单元关系的差别；F(G1,G2)为指挥控制关系模式G1和指挥控制关系模式G2中指挥控制单元之间协作关系的差别。其中

(2)由于在整个指挥控制关系结构模式中,一个被指挥控制单元变化了它的隶属关系,这样必将会使在整个结构模式中某一个指挥控制单元增加一个被指挥控制单元,而另一个指挥控制单元刚好减少这个被指挥控制单元。因此,两个指挥控制关系结构模式间最大可能的指挥控制单元与被指挥控制单元之间指挥关系差别为2N。

(3)在指挥控制关系结构模式中,不论是在两个指挥控制单元之间删除一条己有的协作关系还有建立一条新的协作关系,这两种变化方式对于整个指挥控制关系结构方案所带来的结构变化代价是相同的。因此,关系结构模式中的指挥控制单元之间从没有任何一条协作关系到两两之间都有相互的协作关系之间的差别为K(K-1)/2。

2.3性能代价

(4)式中,Gi表示执行任务阶段i的任务分配方案Si的指挥控制关系模式。

2.4演化代价

(5)

2.5指挥控制关系适应性演化的数学模型

以指挥控制关系的适应性演化方案Δ为决策变量的极小化演化代价CE(Δ)的指挥控制关系适应性演化问题的数学模型为

(6)

式中,CE(Δ)为指挥控制关系适应性演化方案Δ的演化代价函数;Π为指挥控制关系适应性演化方案的集合,是整个优化模型的解空间,并且解空间是有限的;GΔi(t)t为演化方案Δi中的一个节点,表示演化方案Δi在任务阶段t选择的指挥控制关系;Yt为执行任务阶段t的任务分配方案的可行指挥控制关系的集合,也是有限的。

3指挥控制关系适应性演化问题模型的求解方法

由式(6)的指挥控制关系适应性演化问题的数学模型可知,要对问题模型进行求解,主要解决问题模型中的两个子问题:每个任务阶段t(t=1,2,…,L)可行的指挥控制关系集合Yt的产生,在产生的Yt基础上搜索相邻任务阶段间最佳的指挥控制关系的演化路径。

针对问题模型中两个子问题,本节提出的求解方法整体思路是:采用基于n-Best策略[9-12]的层次聚类方法获取每个任务阶段可行的指挥控制关系集合,使用遗传算法(genetic algorithms, GA)搜索最优的演化路径。

3.1基于n-Best策略层次聚类的可行指挥控制关系集合的产生

由文献[6-8]可知,采用基于层次聚类方法可以求得某一任务阶段t(i=1,2,…,L)的任务分配方案Si(i=1,2,…,L)的最优指挥控制关系,本节在此方法的基础上,提出了基于n-Best策略的层次聚类方法来求得某一任务阶段t(t=1,2,…,L)的任务分配方案St(t=1,2,…,L)的可行指挥控制关系集合。基于n -Best策略的层次聚类方法的具体流程如图3所示。

由图3可知,针对每个任务阶段t(t=1,2,…,L)的不同St(t=1,2,…,L),产生可行的指挥控制关系集合的过程实质上是被指挥控制单元的聚类问题,当被指挥控制单元的分组数量Know≥(K+D)(K为指挥控制单元的数量,也就是最终的被指挥控制单元分组的数量;D为常数,D≥0,用于控制产生可行指挥控制关系集合的最大数量)的时候,每次产生一个最佳的被指挥控制单元合并选项,具体的过程可参考文献[6],在这里就不再赘述,具体的合并规则有基于最小矢量距离合并规则[6,13]、基于最小工作负载合并规则[6,13]和基于最小工作负载均方根(root mean square, RMS)[6],本文设计的层级聚类方法采用的合并规则是基于工作负载的RMS合并规则,合并规则中有关指挥控制单元工作负载的定义方法也可参考文献[6-8]。而当被指挥控制单元的分组数量Know<(K+D)的时候,每次产生n-Best个最佳的被指挥控制单元合并选项。由图3可知,使用基于n-Best策略的层次聚类方法求得可行的指挥控制关系集合的关键步骤是n-Best个最佳的被指挥控制单元合并选项产生和集合中不满足性能要求的指挥控制关系的裁剪,如图3中虚线框内部分所示,本节以下内容就是这两部分的具体描述。

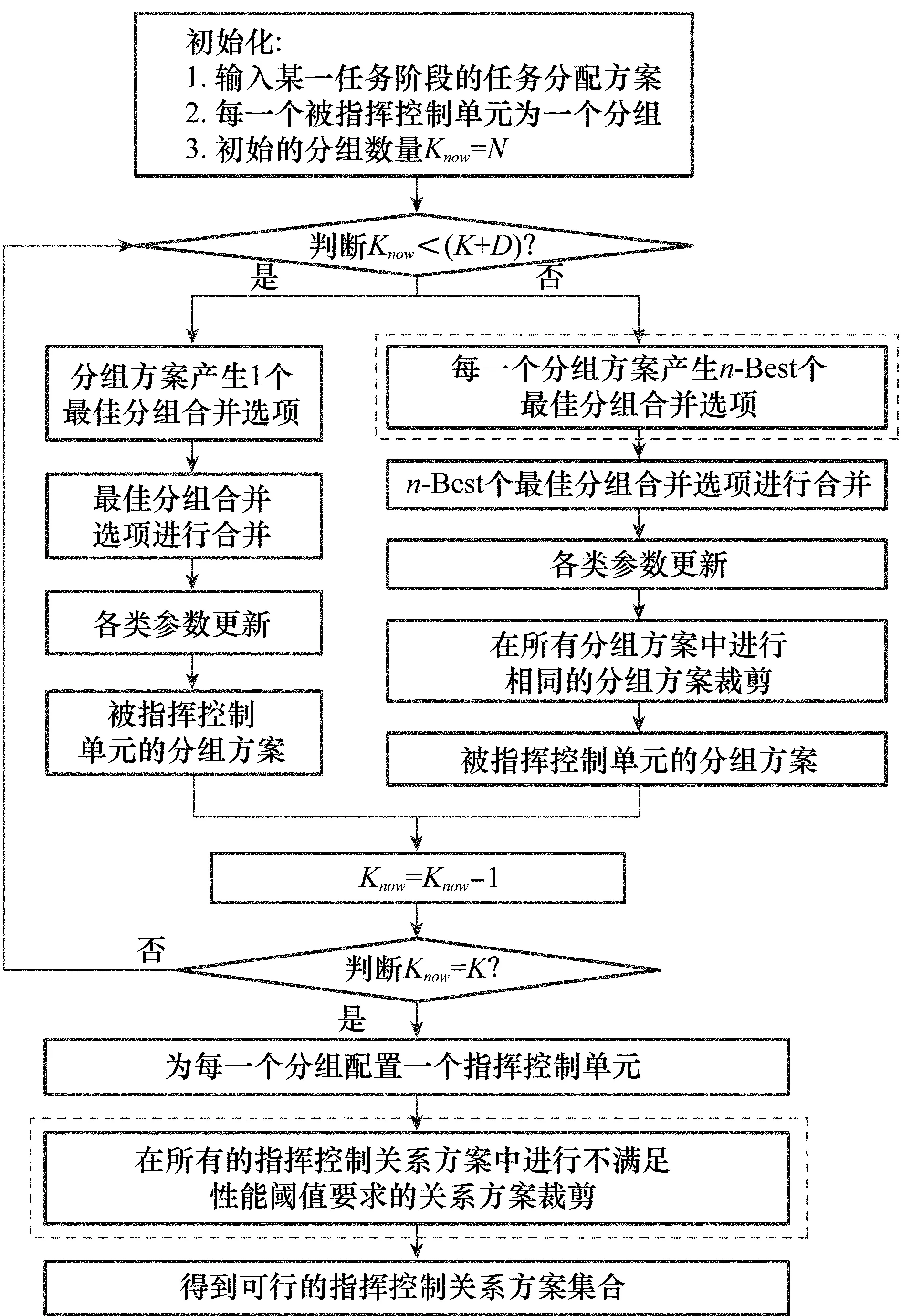
图3　基于n -Best策略的层次聚类方法流程图

3.1.1n-Best个最佳的被指挥控制单元合并选项产生

采用基于工作负载的RMS合并规则来产生n-Best个最佳的被指挥控制单元合并选项,这一操作可以使用如下具体步骤来实现。

步骤 1任意选择两个被指挥控制单元分组进行合并操作。假设在进行被指挥控制单元分组合并之前,存在着Know个被指挥控制单元的分组,从这Know个被指挥控制单元的分组中任意取出两个被指挥控制单元的分组,记为Bh和Bk(h,k=1, 2,…,Know且h≠k),合并Bh和Bk为新的分组Bg。

步骤 2计算新的分组Bg以及其余Dnow-2个分组的工作负载,并计算这Dnow-1个分组工作负载的RMS值,具体详细的方法见文献[6-8]。

步骤 3选择结构性能最佳的前n个(n-Best)合并选项。假设被指挥控制单元的分组数量为Know,这样的话,所有可能的被指挥控制单元分组合并方案的数量为Know·(Know-1)/2个,选择所有合并方案中RMS值最小的前n个进行下一次的合并。

假设1stBest的合并选项为(r,s),则

(7)

假设2ndBest的合并选项为(u,v),则

(8)

由以上步骤可知,如果没有迭代中裁剪的环节和最后对不满足指挥控制关系执行任务分配方案性能阈值要求的关系方案裁剪环节,每一次迭代1个分组方案就有n个不同的合并选项,就会产生n个不同合并结果,这样,最多可以产生nD个指挥控制关系方案,而通过方法中两次裁剪环节产生的可行指挥控制关系集合的数量一般要小于nD。

3.1.2对集合中不满足性能要求的指挥控制关系的裁剪

(9)

式中,fmatch为指挥控制关系模式Gt与任务阶段的任务分配方案St在性能上是否匹配的阈值。

3.2基于GA的最优演化路径搜索

由式(6)指挥控制关系适应性演化问题的数学模型可知,搜索最优演化路径的问题是一个复杂的多阶段决策问题。由于指挥控制关系适应性演化过程是前后关联的,并且具有后效性的影响,因此不适合使用常见的动态规划方法对其进行求解[14],而GA作为一种启发式智能搜索方法,经常被用来求解这样的多阶段的具有后效影响的动态决策问题[15]。本文采用GA来搜索指挥控制关系适应性演化问题的最优演化路径。

3.2.1染色体的编码方式

因此,可采用整数型的编码方式对染色体进行编码:一个染色体就是一条演化路径,它由L个整数构成的有序序列Z=(z1,…,zt,…,zL)组成,其中zt∈{1,2,…,ht},t=1,2,…,L，zt=i表示选择第t(t=1,2,…,L)个任务阶段可行的指挥控制关系方案集合为ΩGt中的第i个指挥控制关系。

3.2.2适应度函数

由式(6)可知,评判一个染色体性能好坏的标准是该染色体的演化代价,即演化路径的演化代价,一个染色体的演化代价越小,该染色体的性能越优。因此,本文采用染色体演化代价CE(Δ)的倒数为GA的适应度函数

(10)

3.2.3遗传算子

(1) 交叉算子

(11)

(12)

(2) 变异算子

(13)

式中,V(1,ht)表示区间[1, ht]内的一个随机整数。

(3) 选择算子

将交叉种群(初始种群进行交叉操作后得到的种群)、变异种群(初始种群进行变异操作后得到的种群)以及初始种群3个种群进行合并操作,得到合并种群,采用式(10)计算适应度值的方法计算这个合并种群中每个染色体的适应度值,使用以下选择方法进行选择操作:精英策略(使得操作中得到的最优个体能够保存下来)和赌轮盘(能够保持个体的多样性)两种选择方式相结合。

3.2.4算法步骤

步骤 1采用本文的编码方式随机产生ND个染色体,这一初始种群记为NI;

步骤 2对初始种群NI分别进行概率为Pc的交叉操作和概率为Pm的变异操作,分别产生交叉种群NC和变异种群NM;

步骤 3将3个种群进行合并操作,并进行选择,产生一个新的种群,并替代NI;

步骤 4重复步骤2~步骤3直至最大迭代次数。

4算例分析

以C4ISR系统执行某一联合作战的战役想定为仿真算例,在计算机上使用Java程序进行分析和验证。假设联合作战的战役想定中有36个作战任务,N=20个被指挥控制单元,并且假设有K=5个指挥控制单元;设该作战想定中某一次规划的任务分配方案的甘特图如图4所示(C4ISR系统指挥控制关系适应性演化问题的输入是已知的)。

图4　某一任务分配方案的甘特图

由军事领域专家给出该任务分配方案任务阶段的个数L=5,演化时间点分别为{70,135,180, 230},如图4中的红线所示,基于n-Best策略的层次聚类方法中的参数设置为:n=2,D=6,WR=1,WP=3,WA=1,WC=1,Pmatch=95%。关于指挥控制单元工作负载的定义方法和参数设置可以参考文献[6-8];而GA的参数设置为ND=20,Pc=0.8,Pm=0.2,最大迭代次数为100。

按照算例的以上设置,做了以下仿真实验。

仿真实验1采用本文提出的基于n-Best策略层次聚类方法得到5个任务阶段可行的指挥控制关系集合以及它们的性能值如图5所示,理论上每个任务阶段最多可行的方案个数为nD=26=64个,而由图5可知,每个任务阶段可行的指挥控制关系的数量分别为{20,18,11,16,5},要小于理论上的最大值,是因为基于n-Best策略层次聚类方法在n-Best个最佳方案合并环节可能会产生很多重复的方案,以及产生的指挥控制关系可能不能满足性能阈值的要求。

图5　基于n -Best策略层次聚类方法得到的各任务阶段可行的指挥控制关系方案以及演化路径

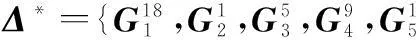
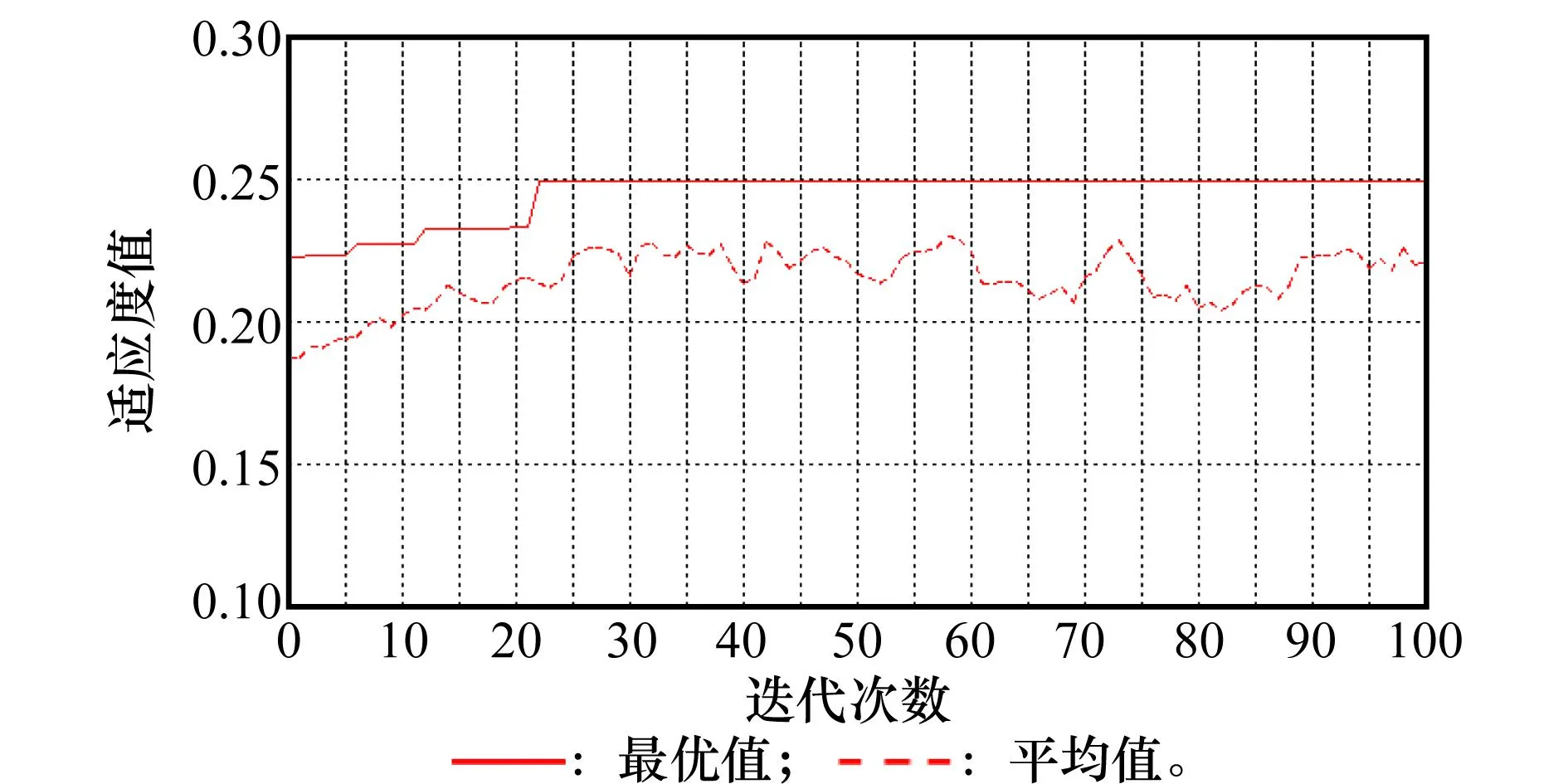
图6　GA的收敛曲线

仿真实验2为了进一步验证求解方法的可行性,做了100次GA搜索最优解的仿真实验,来验证GA搜索最优解的稳定性(即:是不是每次GA都能够得到最优解,是不是有时会陷入局部最优,陷入的局部最优解与最优解的差距如何),这100次GA搜索得到的最优解的变化曲线如图8所示,由图8可知,100次GA中只有4次不能得到最优解,并且这4次得到的解也非常接近最优解,这4次解的平均优化率为96.673 9%,可以得出本文设计的GA具有较强的稳定性。

图7　GA搜索得到的最优指挥控制方案演化形式

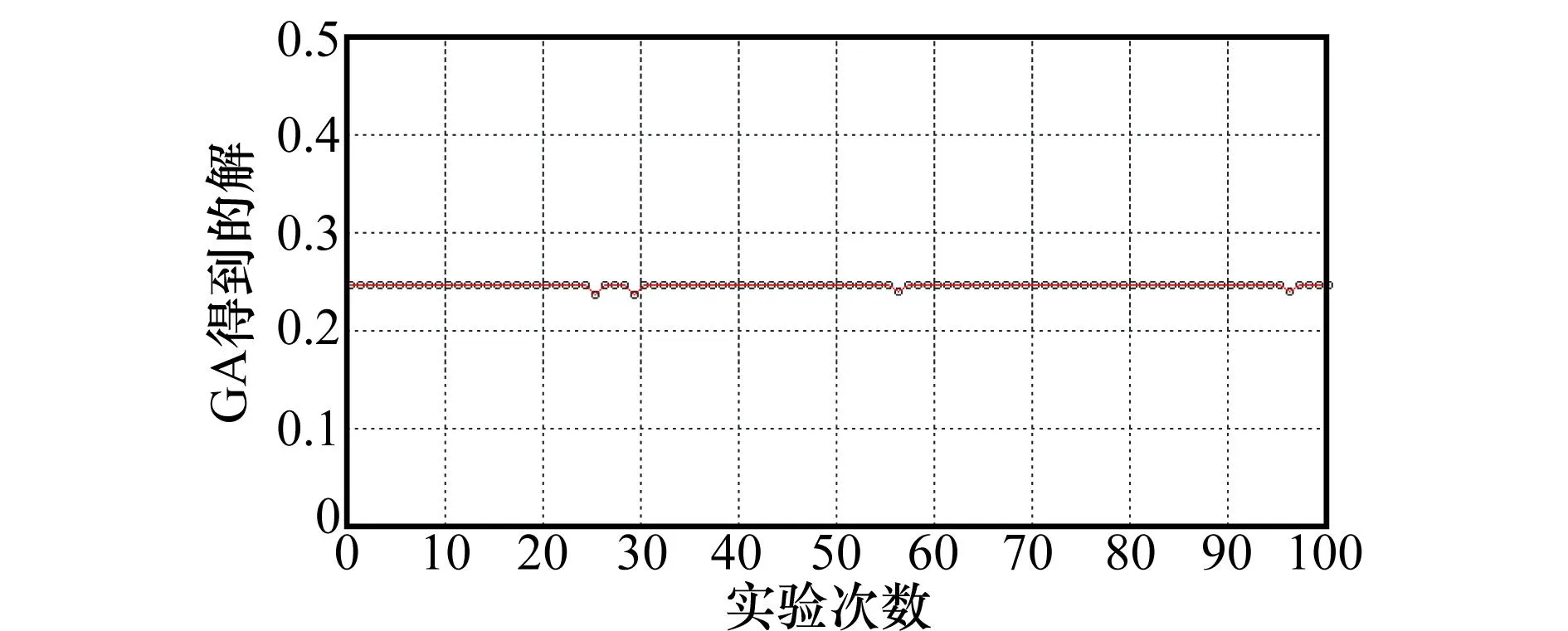
图8　100次GA得到最优解的变化曲线

5总结

本文针对C4ISR系统结构中指挥控制关系的适应性演化问题,构建了指挥控制关系适应性演化的模型及其求解方法。通过对指挥控制关系适应性演化过程的分析和描述,在设计指挥控制关系结构变化代价和性能代价的基础上,构建了指挥控制关系适应性演化问题的数学模型,并针对所建的数学模型,提出了基于n-Best策略层级聚类方法以及GA的问题求解方法,最后通过算例的仿真结果说明本文所提方法有效、可行。

但是本文的模型存在着以下不足:①本文所建指挥控制关系模型中只考虑了指挥控制单元与被指挥控制单元之间的指挥控制关系以及指挥控制单元之间的协作关系,而真正意义上的指挥控制关系模式在指挥控制单元之间应该也是指挥控制关系,就是要将指挥控制单元之间协作关系转化为指挥控制关系的问题,关于这个问题的解决可以借鉴在C2组织设计三阶段方法中第三阶段[7]的求解思路;②在基于n-Best策略的层次聚类方法产生可行的指挥控制关系集合过程中,参数n以及D的设置直接关系每个阶段可行的指挥控制关系的数量,这两个参数的设置带有很强的主观性,在很多时候比较难以把握,因此,需要重点研究这两个参数的设置问题。这些将是本文指挥控制关系适应性演化问题下一步的研究工作。

参考文献：

[1] Lan Y S. Understanding the network-centered command information system[J].CommandInformationSystemandTechno-logy, 2010, 1(1): 1-4. (蓝羽石. 对以网络为中心的指挥信息系统的认识[J]. 指挥信息系统与技术, 2010, 1(1): 1-4.)

[2] Lan Y S, Wang H, Zhang G N, et al. Network centric architecture for C4ISR system[J].CommandInformationSystemandTechnology, 2013, 4(6): 1-6. (蓝羽石, 王珩, 张刚宁, 等. C4ISR系统网络中心体系架构[J]. 指挥信息系统与技术, 2013, 4(6): 1-6.)

[3] Lan Y S, Yi K, Wang H, et al. Delay assessment method for networked C4ISR system architecture[J].SystemsEngineeringandElectronics,2013,35(9):1908-1914.(蓝雨石,易侃,王珩,等.网络化C4ISR系统结构时效性分析方法[J].系统工程与电子技术,2013,35(9):1908-1914.)

[4] Cares J R. An information age combat model[C]∥Proc.ofthe9thInternationalCommandandControlResearchandTechnologySymposium, 2004:1-27.

[5] Wang X, Yao P Y, Zhou X X, et al. A new evaluation on node importance in command information system[J].JournalofBeijingUniversityofPostsandTelecommunications,2011,34(4):38-42.(王欣,姚佩阳,周翔翔,等.指挥信息系统网络节点重要度评估方法[J].北京邮电大学学报,2011,34(4):38-42.)

[6] Zhang J Y, Yao P Y. Model and solving method for collocating problem of decision-makers in C2 organization[J].SystemsEngineeringandElectronics, 2012, 34(4): 737-742. (张杰勇, 姚佩阳. C2组织决策实体配置问题建模与求解方法研究[J]. 系统工程与电子技术, 2012, 34(4):737-742.)

[7] Levchuk G M, Levchuk Y N, Meirina C, et al. Normative design of project-based organizations-part III: modeling congruent, robust, and adaptive organizations[J].IEEETrans.onSystems,ManandCybernetics,PartA:SystemsandHumans,2004,34(3):337-350.

[8] Zhou X X, Yao P Y, Wang X. Command and control resource deployment based on improved hierarchical clustering method[J].SystemsEngineeringandElectronics,2012, 34(3): 523-528. (周翔翔, 姚佩阳, 王欣. 基于改进层次聚类法的指挥控制资源部署[J]. 系统工程与电子技术, 2012, 34(3): 523-528.)

[9] Han X, Bui H, Mandal S, et al. Optimization-based decision support software for a team-in-the-loop experiment: asset package selection and planning[J].IEEETrans.onSystems,Man,andCybernetics:Systems, 2013, 43(2): 237-251.

[10] Park C, Pattipati K R, An W, et al. Quantifying the impact of information and organizational structures via distributed auction algorithm: point-to-point communication structure[J].IEEETrans.onSystems,ManandCybernetics,PartA:SystemsandHumans, 2012, 42(1):68-86.

[11] An W, Park C, Han X, et al. Hidden Markov model and auction-based formulations of sensor coordination mechanisms in dynamic task environments[J].IEEETrans.onSystems,Man,andCybernetics,PartA:SystemsandHumans, 2011, 41(6): 1092-1106.

[12] Mandal S, Han X, Pattipati K R, et al. Agent-based distributed framework for collaborative planning[C]∥Proc.oftheIEEEInternationalConferenceonAerospaceConference,2010:1-11.

[13] Levchuk G M, Levchuk Y N, Luo J, et al. Normative design of organizations-Part II: organizational structure[J].IEEETrans.onSystems,Man,andCybernetics,PartA:SystemsandHumans, 2002, 32(3): 360-375.

[14] Yang C H, Liu J X, Chen H H, et al. Adaptive optimization of agile organization of command and control resource[J].JournalofSystemsEngineeringandElectronics,2009,20(3):558-564.

[15] Wang X P, Cao L M.Geneticalgorithm-theories,applicationsandsoftwareimplementation[M]. Xi’an: Xi’an Jiaotong University Press, 2002. (王小平, 曹立明. 遗传算法-理论、应用与软件实现[M]. 西安: 西安交通大学出版社, 2002.)

张杰勇(1983-),男,工程师,博士,主要研究方向为指挥信息系统工程、指控组织设计。

E-mail:dumu3110728@126.com

蓝羽石(1954-),男,研究员级高级工程师,主要研究方向为电子信息系统总体技术、电子信息系统一体化技术。

E-mail:luyushi@gmail.com

易侃(1981-),男,高级工程师,博士,主要研究方向为系统体系结构、信息栅格和面向服务技术。

E-mail:yikan@gmail.com

毛少杰(1963-),男,研究员级高级工程师,主要研究方向为系统仿真与评估。

E-mail:maoshaojie@gmail.com

王珩(1977-),男,高级工程师,博士,主要研究方向为系统体系结构、信息栅格。

E-mail:wangheng@gmail.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20141019.2345.009.html

Model and solving method for adaptive evolution of command and

control relationship in C4ISR system

ZHANG Jie-yong1,2, LAN Yu-shi1, YI Kan1, MAO Shao-jie1, WANG Heng1

(1.ScienceandTechnologyonInformationSystemsEngineeringLaboratory,The28thResearch

InstituteofChinaElectronicsTechnologyGroupCorporation,Nanjing210007,China; 2.Collegeof

InformationandNavigation,AirForceEngineeringUniversity,Xi’an710077,China)

Abstract:The adaptive evolution of command and control (C2) relationship in C4ISR system structure is studied. The model of the C2 relationship is established, the process of the C2 relationship adaptive evolution is analyzed and depicted, the cost of structure change and the cost of performance are designed, and the mathematic model with the value of sum of evolution cost minimization as the objective function is built for the problem of the C2 relationship adaptive evolution. Then the method based on the n-Best strategy hierarchical clustering algorithm and genetic algorithm (GA) to solve this model is designed. The hierarchical clustering algorithm based on n-Best strategy is used for getting the feasible C2 relationship in each task window, and the GA is used for searching the best path of evolution. Finally, the applicability and stability of this solving algorithm are illustrated by a case of joint operational plan.

Keywords:C4ISR system; command and control relationship; adaptive evolution; n-Best strategy; hierarchical clustering algorithm; genetic algorithms (GA)

作者简介：

中图分类号：E 919; C 394

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2015.07.13

基金项目：总装预研基金(513060204)资助课题

收稿日期：2014-04-21；修回日期：2014-07-29；网络优先出版日期：2014-10-19。