基于特殊阵列的近场源参数估计新算法

司伟建, 李晓林, 蒋伊琳

(哈尔滨工程大学信息与通信工程学院, 黑龙江 哈尔滨 150001)



基于特殊阵列的近场源参数估计新算法

司伟建, 李晓林, 蒋伊琳

(哈尔滨工程大学信息与通信工程学院, 黑龙江 哈尔滨 150001)

摘要：阵列孔径损失和计算复杂度大是近场源参数估计面临的两大亟待解决的问题,提出一种类似NEST阵列模型的新模型,利用四阶累积量扩展阵列孔径,使可估计信源个数远远大于实际阵元数;并结合基于特征方程算法(characteristic equation-based method, CEM)思想避免特征值分解和谱峰搜索,极大降低了算法的计算复杂度。最后,基于已获得的近场源的角度信息,估计出所有近场源的距离信息。理论分析和实验仿真结果表明,在保证参数估计精度的前提下,所提算法的计算复杂度低,具有较高的阵列利用率,并且可以避免二维参数配对。

关键词：阵列信号处理; 高阶累积量; 阵列孔径扩展; 基于特征方程算法; 多项式求根

0引言

信源定位技术是阵列信号处理领域的一个重要分支,其广泛应用于雷达、通信、声呐等领域。目前大量算法都是针对远场信号,例如多重信号分类(multiple signal classification, MUSIC)算法[1]和旋转不变子空间(estimation of signal parameters via rotational invariance techniques, ESPRIT)算法[2]等。然而当信源与接收阵列之间的距离在菲涅尔域内时,信源发射的信号以球面波的形式而不是平面波形式穿过阵列,远场信号的假设不再成立,信源的位置需要由角度信息和距离信息共同确定,此时的定位为近场源定位。

近场源定位在语音增强、移动通信和电子侦察等领域中有着广泛的应用,因此针对近场信号参数估计的算法[3-13]得到广大学者的重视。文献[3]给出了最大似然估计算法估计近场信号参数;文献[4-5]运用二维MUSIC的思想进行近场源参数估计;文献[6-7]给出了高阶累积量ESPRIT算法;文献[8]将对称阵列分为两个子阵列,利用子阵列之间的对称关系构造谱函数进行参数估计。上述算法都是在均匀线阵的基础上进行推导,可估计信源的个数不能超过阵元个数甚至不能超过阵元个数的一半,严重损失阵列的自由度;且上述算法都需要特征值分解和谱峰搜索,导致计算复杂度大,计算复杂度随阵元数增加而增大。为了提高阵列利用率,文献[14]针对远场信源参数估计提出一种NEST阵列模型,此模型可以有效地增加天线自由度,使其能够估计的信源数大于实际的天线个数;文献[15]将NEST阵列模型应用于混合信号参数估计中;本文提出一种类似于NEST阵型的新阵列模型,并结合四阶累计量进行参数估计大大增加天线自由度。和文献[15]相比,在相同的阵元数条件下本文能够估计更多的信源数。为了降低运算复杂度,CEM算法在文献[16]首次被提出,该算法无需特征值分解和谱峰搜索,通过构造一个多项式即可获得参数信息;基于CEM算法[17-18],文献[18]将其思想运用到非相干与相干混合信源参数估计问题;本文将该理论运用到近场信源参数估计用来降低运算复杂度。

1信号模型

本文所用阵列模型如图1所示,阵列包括2(M+N)+1个各向同性的阵元,由3个子阵列组成。子阵1由2N+1个阵元组成,阵元间距为d,子阵2和子阵3分别由M个阵元组成,阵元间距为(2N+1)d,且分别位于子阵1两侧,距离中心阵元的距离为(3N+1)d。

图1　特殊的稀疏对称阵列

假设有L个相互独立的窄带近场信号入射到稀疏对称阵列上,以中心阵元为相位参考点,则第n个阵元接收数据表示为

(1)

式中,K为快拍数;sk(t)为第k个信源的信号波形;wn(t)为第n个阵元接收的加性噪声;pn为第n个天线与参考阵元之间的距离;ωk，φk分别表示为

(2)

式中,λ为信号波长;θk,rk分别为第k个近场信号的角度参数和距离参数。

将天线接收数据写成矢量形式为

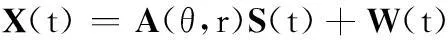
(3)

式中,X(t)=[x1(t),x2(t),…,x2(N+M)+1(t)]T为x轴阵元接收的数据矢量;W(t)=[w1(t),w2(t),…,w2(N+M)+1(t)]T为x轴阵元接收的噪声矢量;S(t)=[s1(t),…,sL(t)]T代表L个独立窄带近场信号;A(θ,r)为(2(N+M)+1)×L维阵列导向矢量,表示为

(4)

式中,a(θk,rk)表示为

(5)

在本文中,对信号模型进行如下假设:

假设 1L个信源之间相互统计独立,具有非零峰度的非高斯过程。

假设 2每个阵元上接收的噪声是零均值的高斯过程,且与信号不相关。

假设 3为了确保参数估计的唯一性,要求d≤λ/4。

2基于稀疏对称阵列的近场目标定位算法

2.1近场信号角度参数估计

由于将高阶累积量应用于空间谱估计算法中可以抑制高斯噪声,同时可以获得如阵列孔径扩展、阵元误差校正等优良性能,因此基于高阶累积量的空间谱估计算法得到广泛的关注。文中采用四阶累积量的计算公式为

(6)

首先,利用子阵1构造矩阵C1为

(7)

为了方便下一步推导,定义函数:

(8)

通过观察式(7)可以看出矩阵C1是一个复Toeplitz矩阵,可以表示为

C1=

(9)

将矩阵C1斜对角线相加即可得到z1的估计值。

(1) 当k=-1,-2,…,-2N时

(10)

(2) 当k=0,1,…,2N时

(11)

利用子阵2同子阵1构造M(2N+1)维矩阵C2,表示为

(12)

令

z2=vec(C2)

(13)

即

(14)

利用子阵3同子阵1构造M(2N+1)维矩阵C3,表示为

(15)

令

z3=vec(C3)

(16)

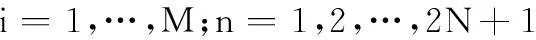
(17)

将z1,z2,z3重新组合得到(4N+1)+2(2N+1)M维向量z,表示为

z=[z2z1z3]

(18)

为了避免特征值分解和谱峰搜索,降低运算量,结合CEM算法进行算法简化,具体步骤如下:

首先构造一个L阶多项式,表示为

(19)

通过式(19)可以明显看出,它的L个位于单位圆上的根对应于L个信源的角度信息,因此只需要确定多项式系数[cL-1,cL-2,…,c0],构造出式(19),对其进行求解即可得到信源的角度参数。

为了方便推导,设P=2N+(2N+1)M。

将解ej2ωk代入到方程(19)中可以满足式(20)：

(20)

将等式(20)两边同时乘以因子c4siej2ωkJ可得

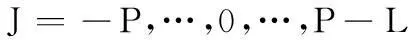
(21)

将式(21)中L个等式相互叠加可得

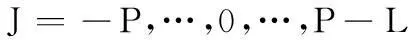
(22)

将式(18)代入到式(22)中,可将式(22)改写为

z(J+1)c1+z(J)c0=0，

(23)

将2P-L+1个等式改写成矩阵形式：

(24)

通过式(24)可以看出只要确定z的值即可求得多项式的系数[cL-1,cL-2,…,c0]。

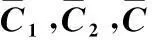
(25)

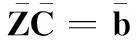
(26)

式中

(27)

(28)

通过求解多项式(28)得到L个根,利用式(29)进行转换得到近场信号的角度参数。

(29)

2.2近场信号的距离参数估计

信源的角度参数估计出以后,下一步进行距离参数估计。首先构造协方差矩阵R,即

(30)

对协方差矩阵R进行特征值分解,可得

(31)

式中,US是由大特征值对应的特征矢量张成的信号子空间;UN是由小特征值对应的特征矢量张成的噪声子空间。利用信号子空间与噪声子空间正交的原理构造新的函数,通过最小化谱函数式(32)得到信号的距离信息。

(32)

传统算法一般都是利用谱峰搜索得到信号的距离信息,然而谱峰搜索的计算复杂度较高,不适合实时处理,且估计精度受搜索步长影响,因此本文采用特征值分解的思想代替谱峰搜索,用来减少运算量。

为了降低特征值分解的维数,将阵列流型进行分解,即

(33)

(34)

(35)

式中,a1(θi)为(2(N+M)+1)×((N+M)+1)维矩阵;a2(r)为(N+M)+1维列向量。

将式(33)代入式(32)中得

(36)

利用式(37)求得近场信源的距离信息

(37)

通过以上算法,将近场信号的角度参数分别代入阵列流型中求得其对应的距离参数,可以避免二维参数配对。

同样,本文算法也适用于近场信号与远场信号并存的情况。

2.3本文算法描述

本文算法步骤如下:

步骤 1利用式(6)构造高阶累计量矩阵C1、C2、C3。

步骤 2对3个高阶累计量矩阵C1、C2、C3分别进行处理,利用式(10)和式(11)对C1进行处理得到向量z1;对矩阵C2、C3进行向量化分别得到向量z2和z3,将得到的3个向量z1、z2和z3重新组合得到新的向量z。

步骤 4构造数据协方差矩阵R,并对其进行特征值分解,求得小特征值对应的噪声子空间UN。

3算法性能分析

考虑本文算法、two-stage MUSIC (TSMUSIC)算法和mixed-order MUSIC (MOMUSIC)算法在相同阵元数条件下最大可估计信源个数,假设有Q个阵元,其中子阵1由2N+1个阵元组成,子阵2和子阵3由M个阵元组成,TSMUSIC算法最多可以估计Q-1个信号源,MOMUSIC算法最多可估计M+N+MN个信源,本文算法可估计(2N+1)+(2N+1)M。通过上述分析可以看出,本文算法可估计信源的个数远远大于MOMUSIC算法和TSMUSIC算法,随着子阵1的阵元数的增加本文算法的优越性越明显。

3种算法运算量对比,由于构造累积量矩阵、特征值分解和谱峰搜索这3步需要较大的运算量,因此主要考虑这3步进行运算量分析。 TSMUSIC算法需要构造一个Q×Q维的四阶累积量,MOMUSIC算法构造一个2(M+1)(N+1)维向量;本文算法需要构造一个N×N维四阶累积量和2M(2N+1)维向量,从构造矩阵角度考虑,TSMUSIC算法运算量远远大于MOMUSIC算法和本文算法,而本文算法略高于MOMUSIC算法;利用CEM思想,文算法只需构造一个多项式并对其进行求解得到角度参数,无需进行特征值分解和谱峰搜索;而TSMUSIC算法和MOMUSIC算法均需要特征值分解和谱峰搜素,大大增加运算复杂度,综上所述可以看出,本文算法的运算量要小于TSMUSIC算法和MOMUSIC算法。

4数据仿真

为了验证所提算法的优良性能,将本文所提算法与TSMUSIC算法、MOMUSIC算法进行比较,阵列摆放形式如图1所示。仿真条件如下:阵元数为17,最小阵元间距为λ/4,进行1 000次蒙特卡罗实验。实验中使用根均方误差(root mean square error, RMSE)作为性能评价标准。

式中,ρ为参数估计值;ρtrue为参数真值;N为蒙特卡罗实验次数。

实验 1入射信号2个窄带近场信号,位置分别为(30°,4λ)和(35°,2λ),噪声模型为高斯白噪声,仿真条件如上所述。

(1) 不同信噪比下各算法测向性能比较:快拍数为200,信噪比从0~40 dB不断变化,步长为5 dB,图2和图3分别表示了角度参数和距离参数的估计性能。从图2可以看出,本文算法的角度估计精度高于TSMUSIC算法和MOMUSIC算法。MOMUSIC算法运用数据量较少,因此估计性能最差;本文算法运用新的阵列摆放形式,有效扩展了阵列孔径,因此估计性能优于TSMUSIC算法,与此同时,本文算法结合了估计性能更好的多项式求根算法,无需谱峰搜索,精度不受搜索步长的影响。从图3可以看出,本文算法的距离估计精度高于TSMUSIC算法和MOMUSIC算法,这是由于距离的估计是在角度估计基础之上进行的,受到角度估计精度的影响。

图2　3种算法随信噪比变化的角度估计性能比较图

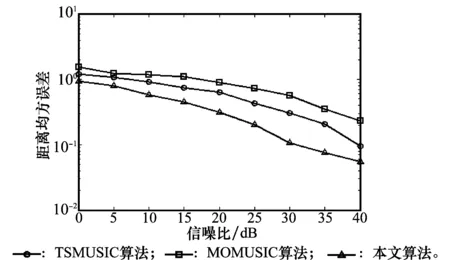
图3　3种算法随信噪比变化的距离估计性能比较图

(2) 不同快拍数下各算法测向性能比较:信噪比为20 dB,快拍数从10~400不断变化,步长为50,图4和图5分别示出了角度参数和距离参数的估计性能。从图4可以看出,由于3种算法均采用高阶累积量进行参数估计,因此受快拍数影响比较大,快拍数越大,算法性能越高,本文算法的角度参数估计性能高于TSMUSIC算法和MOMUSIC算法。从图5可以看出,本文算法的距离估计精度高于TSMUSIC算法和MOMUSIC算法,这是由于距离的估计是在角度估计基础之上进行的,受到角度估计精度的影响。

图4　3种算法随快拍数变化的角度估计性能比较图

图5　3种算法随快拍数变化的距离估计性能比较图

实验 2入射信号4个窄带信号,其中包括2个近场信号和2个远场信号,近场信号的位置分别为(30°,4λ)和(35°,2λ),远场信号的位置分别为40°和50°,噪声模型为高斯白噪声。

(1) 不同信噪比下各算法测向性能比较:快拍数为200,信噪比从0~40 dB不断变化,步长为5 dB。图6和图7分别示出了角度参数和距离参数的估计性能。从图6可以看出,本文算法的角度估计精度高于TSMUSIC算法和MOMUSIC算法。由于采用新的阵列模型,有效地扩展阵列孔径,因此估计性能由于其他两种算法;并结合与此同时本文算法结合了估计性能更好的多项式求根算法,精度不受搜索步长的影响。从图7可以看出，本文算法的距离估计精度高于TSMUSIC算法和MOMUSIC算法,这是由于距离的估计是在角度估计基础之上进行的,受到角度估计精度的影响,角度估计精度越高,距离的估计精度就越高。

(2) 不同快拍数下各算法测向性能比较:信噪比为10 dB,快拍数从10~400不断变化,步长为50。图8和图9分别示出了角度参数和距离参数的估计性能,从图8中可以看出,当快拍数较低的时候,3种算法的角度参数估计性能较差,随着快拍数增大,3种算法的估计性能变好,本文算法的角度估计性能和距离参数估计性能均高于TSMUSIC算法和MOMUSIC算法。

图6　混合信源条件下3种算法随信噪比变化的角度估计性能比较图

图7　混合信源条件下3种算法随信噪比变化的距离估计性能比较图

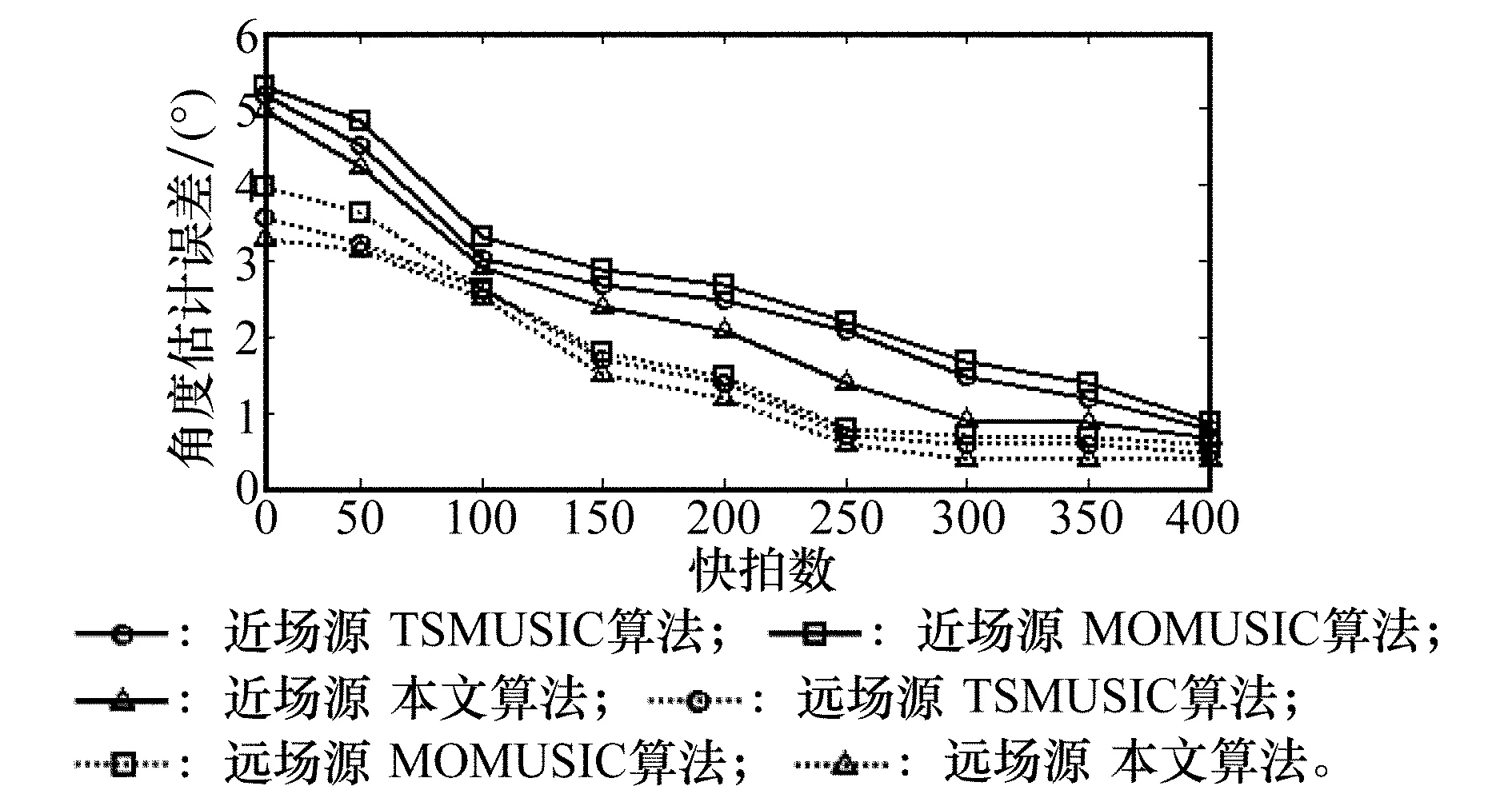
图8　混合信源条件下3种算法随快拍数变化的角度估计性能比较图

图9　混合信源条件下3种算法随快拍数变化的距离估计性能比较图

实验 3入射信号2个窄带近场信号,位置分别为(30°,4λ)和(35°,2λ),噪声模型为高斯白噪声,信噪比为20 dB, 快拍数为200,阵元数从11~21不断增加,统计仿真时间如表1所示。由于阵元数增大,算法所需要处理的矩阵的维数增大,因此复杂度变大。与上述理论分析一致,3种算法随着阵元数的增加,运行时间逐渐增大。从表1中可以明显看出本文算法的运行时间远远小于TSMUSIC算法和MOMUSIC算法。由于TSMSUIC算法和MOMUSIC算法需要特征值分解和谱峰搜索,因此其受阵元数的影响比较大;而本文算法无需特征值分解和谱峰搜索,因此其受阵元数的影响比较小。随着阵元数的增大,本文算法的优越性能更加突出。

表1　算法运行时间比较

实验 4入射信号为12个窄带近场信号,位置分别位于(60°,5λ)、(50°,6λ)、(40°,4λ)、(30°,5λ)(20°,5λ)(10°,6λ)(-60°,6λ)(-50°,4λ)(-40°,5λ)(-30°,3λ)(-20°,5λ)(-10°,3λ),阵元数为13(其中N=4;M=2),信噪比为20 dB,快拍数为200,为了能够从图中形象看出本文算法的阵列孔径扩展性能,在求解近场信号角度参数时采用谱峰搜索代替求根算法。本文算法仿真谱图如图10所示;TSMUSIC算法仿真图如图11所示。从图11可以明显看出,本文算法可以清晰的分辨出12个角度,并形成尖锐的谱峰;而TSMUSIC算法则分辨不出角度。通过仿真可知本文算法采用的特殊阵列模型,并结合四阶累积量,相对于TSMUSIC算法有明显的阵元自由度扩展。

图10　本文算法仿真图

图11　TSMUSIC算法仿真图

5结论

本文提出一种高精度、低复杂度的近场源参数估计算法,采用类似于NEST阵型的新阵列模型,结合四阶累积量进行阵列扩展,有效地提高了算法可估计信源数,使其可远远大于阵元数;并结合CEM思想用于降低运算复杂度。与此同时,本文算法同样适用于近场与远场混合信源定位。从数据仿真结果可以看出本文算法的有效性。增大阵元之间的间距可以得到更高的估计精度,然而本文阵元的最小间距不能超过波长的四分之一,否则会产生模糊估计,如何增大此阵列模型阵元之间的间距,同时正确估计信号参数成为下一步要解决的问题。

参考文献：

[1] Schmidt R O. Multiple emitter location and signal parameters estimation[J].IEEETrans.onAntennasandPropagation, 1986, 34(3): 267-280.

[2] Zhang X, Xu D. Low-complexity ESPRIT based DOA estimation for collocated MIMO radar using reduced-dimension transformation[J].ElectronicsLetters, 2011, 47(4):283-284.

[3] Swindlehurst A L, Kailath T. Passive direction of arrival and range estimation for near-field sources[C]∥Proc.ofthe4thAnnualASSPWorkshoponSpectrumEstimationandModeling,Minneapolis, 1988:123-128.

[4] Huang Y D, Barkat M. Near-field multiple sources localization by passive sensor array[J].IEEETrans.onAntennasPropagation, 1991, 39(7): 968-975.

[5] Russel J, Kristine L B, Van Trees H L. Broadband passive range estimation using MUSIC[C]∥Proc.oftheInternationalConferenceonAcoustics,SpeechandSignalProcessing(ICASSP), 2002:2920-2923.

[6] Challa R N, Sham Sunder S. Higher-order subspace based algorithms for passive localization of near-field sources[C]∥Proc.ofthe29thAsilomarConferenceSignals,SystemsandComputersCalifornia:IEEEComputerSocietyPress, 1995: 777-781.

[7] Yuan N, Friedlander B. Performance analysis of higher order ESPRIT for localization of near-field sources[J].IEEETrans.onSignalProcessing, 1998, 46(3):709-719.

[8] Zhi W J, M W Chia. Near-field source localization via symmetric subarrays[J].IEEESignalProcessingLetters, 2007, 14(6):409-412.

[9] Zhou Y, Feng D Z, Liu J Q, et al. A new subspace method for estimation of parameters of near field sources[J].JournalofXidianUniversity,2006,33(1):42-45.(周祎,冯大政,刘建强,等.一种新的近场源参数估计的子空间方法[J].西安电子科技大学学报,2006,33(1):42-45.)

[10] Liang L J, Liu D. Passive localization of mixed near-field and far-field sources using two-stage music algorithm[J].IEEETrans.onSignalProcessing, 2010, 58(1): 108-120.

[11] Liu Z M, Huang Z T, Zhou Y Y. Computationally efficient direction finding using uniform linear arrays[J].IETRadar,SonarandNavigation, 2012, 6(1): 39-48.

[12] Jiang J J, Duan F J, Chen J, et al. High-accuracy localization algorithm for mixed near-and far-field sources[J].JournalofTianjinUniversity(ScienceandTechnology), 2013, 46(12):1114-1120. (蒋佳佳,段发阶,陈劲，等. 一种高精度的近场与远场混合源定位算法[J].天津大学学报(自然科学与工程技术版), 2013, 46(12): 1114-1120.)

[13] Wu Y T, Zhang Y B, Cao H， et al. The fast algorithm for the four dimensional parameter estimation of a single near-field source based on the uniform circular array[J].JournalofWuhanInstituteofTechnology, 2013, 35(3): 75-78. (吴云韬,张彦斌,曹辉,等. 均匀圆阵下单个近场源信号四维参数估快速算法[J].武汉工程大学学报, 2013,35(3):75-78.)

[14] Pal P,Vaidyanathan P P. Nested arrays: a novel approach to array processing with enhanced degrees of freedom[J].IEEETrans.onSignalProcessing, 2010, 58(8): 4167-4181.

[15] Han K Y, Nehorai A. Nested array processing for distributed sources[J].IEEESignalProcessingLetters, 2014, 21(9):1111-1114.

[16] Wang B, Liu J J, Sun X Y. Mixed sources localization based on sparse signal reconstruction[J].IEEESignalProcessingLetters, 2012, 19(8):487-490.

[17] Liu Z M, Huang Z T, Zhou Y Y. Computationally efficient direction finding using uniform linear arrays[J].IETRadar,SonarandNavigation, 2012, 6(1):39-48.

[18] Ma G W, Sha. Z C, Liu Z M, et al. ICA-based direction-of-arrival estimation of uncorrelated and coherent signals with uniform linear array[J].SignalImageandVideoProcessing, 2014, 8(3):543-548.

司伟建(1971-),男,研究员,博士,主要研究方向为宽带系统的信号检测、识别与估计。

E-mail:swj0418@263.net

李晓林(1989-),女,博士研究生,主要研究方向为宽带系统的信号检测、识别与估计。

E-mail:lixiaolinshiwo@163.com

蒋伊琳(1981-),男,博士,讲师,主要研究方向为宽带系统的信号检测、识别与估计。

E-mail:jiangyilin@hrbeu.edu.cn

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20141211.1840.009.html

Algorithm of near-field sources parameter estimation

based on the special array model

SI Wei-jian, LI Xiao-lin, JIANG Yi-lin

(SchoolofInformationandCommunicationEngineering,HarbinEngineeringUniversity,Harbin150001,China)

Abstract:Loss of the array aperture and complicated computation have always been serious problems for parameter estimation of the near-field sources. A new array model is proposed which is similar to the NEST array model, using the forth-order cumulation to extend the array aperture. The number of sources estimated by the proposed algorithm is thus much larger than the number of actual arrays. Moreover, we combine the idea of the characteristic equation-based method (CEM) to avoid eigenvalue decomposition and spectrum peak search, greatly reducing the complexity of computation. Finally, based on the angle information of near-field sources, the range information of near-field sources is estimated. Theoretical analysis and simulation results show that on the premise of the accuracy of parameter estimation, the proposed algorithm has lower computational complexity and higher utilization of arrays, which also avoids two-dimensional parameter matching.

Keywords:array signal processing; high-order cumulation; array aperture extension; characteristic equation-based method (CEM); polynomial root

作者简介：

中图分类号：TN 911.7

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2015.07.02

基金项目：中央高校基本科研业务费专项资金(HEUCF140803)资助课题

收稿日期：2014-08-27；修回日期：2014-12-08；网络优先出版日期：2014-12-11。