基于改进灰色马尔可夫模型的设备故障率预测

李　莉，熊　炜，何　杰 ，袁旭峰，邹晓松

(1. 贵州电力试验研究院，贵州 贵阳550001；2. 贵州大学 电气工程学院，贵州 贵阳550025)

基于改进灰色马尔可夫模型的设备故障率预测

李莉1，熊炜2，何杰2，袁旭峰2，邹晓松2

(1. 贵州电力试验研究院，贵州 贵阳550001；2. 贵州大学 电气工程学院，贵州 贵阳550025)

摘要：电力设备故障率具有时变性、随机性、回退等特点，预测难度大,因此在灰色GM(1,1)模型的基础上，采用模糊C均值聚类方法对GM(1,1)模型拟合值的误差序列进行状态划分；通过计算误差序列的状态转移概率矩阵，建立了电力设备故障率的灰色马尔可夫预测模型。该模型既考虑了GM(1,1)模型较强的处理单调数列的特性，又计及了通过状态转移概率矩阵的变换提取数据随机波动响应的特点，避免了最大概率状态不为实际状态而出现最差的预测结果现象。通过实例证明，基于模糊C均值聚类的灰色马尔可夫模型预测结果优于传统的GM(1,1)模型和基于K均值聚类的灰色马尔可夫预测模型，具有较高的预测精度。

关键词：电力设备故障率；灰色理论；马尔可夫链；模糊C均值聚类

中图分类号：TM774

文献标识码:A

DOI:10.3969/j.issn.1672-0792.2015.08.004

收稿日期：2015-05-21。

基金项目：贵州省科技厅基金(黔科合J字[2011]2060号)。

作者简介：李莉( 1968-)，女，高级工程师，主要从事电力系统可靠性研究,E-mail:420034562@qq.com。

Abstract：Based on the characteristics of time variation and randomness of power equipment failure rate, this paper proposes a state division method for fitted values error series of GM (1,1) model by fuzzy C means clustering method based on grey GM (1,1) model. By computing the state transition probability matrix of error series, a grey Markov prediction model is established. This model analyzes high ability of GM (1,1) model processing monotone series then explores random fluctuation responses when extracting data through transformation of state transition probability matrix. So the worst prediction results when the maximum probability state is not the actual state can be avoided. The actual case study validates that the grey Markov forecasting model based on fuzzy C means clustering method has better performance than conventional GM (1,1) model and grey Markov forecasting model based on K means clustering, and has higher forecast precision.

Keywords：failure rate of power equipment; grey theory; Markov chain; fuzzy C means clustering

0引言

电力设备故障率预测是电力系统可靠性评估及状态检修决策优化的基础，而电力设备故障率与设备所处的地理位置、气候条件、运行条件等众多因素相关，呈现出时变性和随机性的特点，以及检修后故障率回退现象，导致电力设备故障率的预测难度增大。

目前电力设备故障率预测方法主要包括：基于历史数据的方法、基于设备役龄和健康状态的方法和基于人工智能的方法。其中基于历史数据的预测方法采用统计方法进行建模，要求具备大量的历史数据，且数据不能有周期性变化或突变[1，2]。基于设备役龄和健康状态的故障率预测模型，需要对设备的健康状态进行连续跟踪[3～5]。基于人工智能的电力设备故障预测方法主要是利用BP,RBF等人工神经网络方法研究设备故障率变化规律，需要大量的统计样本，预测结果具有很大的主观性和随机性[6，7]。因此，如何提高电力设备故障率的预测精度，是电力系统可靠性评估及开展状态检修的研究热点。

灰色模型对于序列较短并具有明确上升趋势的数据来说，具有较好的预测效果，但对于随机波动性较大的数据序列预测精度较低，而马尔可夫理论通过状态转移概率描述各随机因素的影响以及各状态之间转移的内在规律，可以弥补灰色模型的不足[8～11]。为此，本文提出了基于模糊C均值聚类的灰色马尔可夫模型对电力设备故障率进行预测，以便能充分利用历史数据，提高随机波动性较大的数列预测精度，拓宽灰色理论的应用范围。

1灰色GM(1,1)模型

(1)设电力设备故障率原始数据序列为：

(1)

其中：

(2)对原始数列进行一次累加：

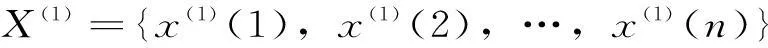
(2)

其中

(3)生成紧邻均值序列：

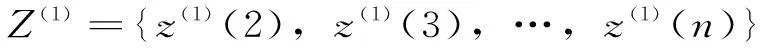
(3)

其中：

(4)建立GM(1,1)模型白化方程：

(4)

其中：a和b是待确定参数。

(5)GM(1,1)模型灰色微分方程为：

(5)

(6)对应的时间响应方程为：

(6)

(7)参数a和b的最小二乘估计为：

(7)

式中：

(8)对预测结果进行累减还原得到预测数列：

(8)

其中：k=1,2,…,n-1

(9)计算预测数列与原始数列的残差：

(9)

式中：

由上可见，GM(1,1)模型是将原始数列经一次累加后进行预测的，由于一次累加数列具有单调性，因此GM(1,1)模型适用于预测指数变化规律的数据，对随机波动型数据则预测误差较大。

2灰色马尔可夫链预测模型

本文采用的灰色马尔可夫预测基本思路，是通过GM(1,1)模型的残差序列计算状态转移矩阵，根据状态转移矩阵对GM(1,1)模型结果进行修正，以提高预测结果的准确性。具体步骤为：

(1)将残差序列E划分为n个状态，任一状态可表示为⊗i(i=1,2,…,n)。

为提高灰色马尔可夫链的预测精度，使残差序列状态划分更科学、更有效，本文采用模糊C均值聚类算法确定残差序列E的分布状态，其算法表述为：

(10)

(11)

(12)

且满足约束条件

(13)

式中：m>1；c是聚类数量；n是聚类空间的样本数；U={μij}表示1个c×n维的矩阵，μij为样本点ej隶属于第i类的程度；J=(U,V)是类内误差的加权平方和目标函数。dij=‖νi-ej‖为第i个聚类中心Vi与第j个数据点ej间的欧氏距离，FCM算法通过迭代式使目标函数最小化，从而达到最佳聚类。

(2)根据残差序列E的状态分布，计算n步转移概率矩阵：

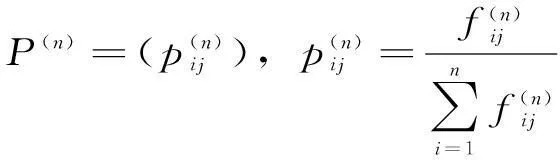
(14)

(4)根据未来不同时刻残差所处的状态，对灰色预测结果进行修正得到预测区间。依据文献[11]中灰色马尔可夫预测方法的讨论，本文采用式(15)计算残差序列的预测值，以避免马尔可夫过程中最大概率状态不为实际状态而出现最差的预测结果现象。

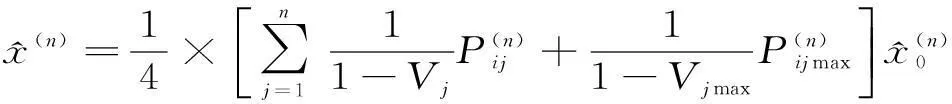
(15)

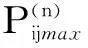
(5)更新原始数据，重复上述步骤，直至完成预测目标。

3算例分析

以某电网2011年6月～2013年12月共31个月220 kV输电线路故障率为原始数据序列，如图1所示。从图中可看出，220 kV输电线路故障率具有时变性、随机性和回退等特点，不能采用时间序列法进行准确预测。

图1　220 kV输电线路故障率数据序列

本文以前26个月的数据为基础数据，建立灰色马尔可夫预测模型进行预测和误差分析。

(1)GM(1,1)预测

采用GM(1,1)预测模型对220 kV输电线路故障率进行预测，时间响应方程为：

x(1)(k+1)=[x(0)(1)-132.716]e0.0026t+132.716

拟合曲线如图2所示。

图2　220 kV输电线路故障率GM(1,1)预测结果

从图2可看出， GM(1,1)模型残差也具有时变、随机分布等特点，能体现设备故障率的变化规律。

(2)对残差序列进行状态划分

为进行对比分析，本文分别采用K均值聚类和模糊C均值聚类对灰色预测数据残差序列进行状态划分，当状态数量为4时，残差序列聚类中心如表1所示，状态分布情况如图3所示。

表1　两种聚类方法获得的残差序列状态中心

图3　GM(1,1)预测数据残差序列状态划分结果

(3)灰色马尔可夫预测模型

分别对上述2种状态划分结果，采用马尔可夫过程对残差序列进行拟合，拟合误差如表2所示，拟合曲线如图4所示。

表2　26个原始数据的灰色马尔可夫拟合误差

图4　26个原始数据的拟合结果与实际值的比较

从表2和图4可看出，2种聚类方法的灰色马尔可夫拟合结果趋势与实际符合，但基于模糊C均值聚类的灰色马尔可夫拟合结果较基于K均值聚类的误差更小，拟合结果更精确。

(4)灰色马尔可夫预测结果

利用基于模糊C均值聚类的灰色马尔可夫预测模型及ARMA模型[12]分别对后5年设备故障率进行预测，预测结果如图5所示，误差如表3所示。

图5　预测结果与实际值的比较

表3　灰色马尔可夫模型及ARMA模型预测误差

从表3和图5可看出，当原始数据随机波动性增大时，基于模糊C均值聚类的灰色马尔可夫预测结果趋势与实际基本相符，均方差较基于K均值聚类的灰色马尔可夫预测、ARMA模型预测小，可见，具有较高的预测精度。

4结论

由于电力设备故障率具有时变性、随机性、回退等特点，本文提出基于模糊C均值聚类的灰色马尔可夫预测方法对电力设备故障率进行预测，通过预测结果的比较，该模型预测优于传统的GM(1,1)模型、基于K均值聚类的灰色马尔可夫预测模型和ARMA预测模型，具有较高的预测精度，为电力系统可靠性的评估及电力设备状态检修的开展提供了可靠的科学依据。但在该模型中，如何引入气候、检修后故障率回退等因素的影响，提高设备故障率非等时间间隔序列的预测精度是下一步研究的重点。

参考文献:

[1]茹斌，张天伟，王宇欣.基于小波去噪及ARMA模型的故障率预测方法研究[J].测控技术,2014,33(10):43-46,50.

[2]顾洁，杜渐,秦杰，等.基于全寿命周期成本的变电站设备检修模糊规划模型[J].电力系统自动化,2014,38(1):44-50.

[3]孙鹏，陈绍辉，张彩庆. 基于Marquardt法参数估计的变电设备寿命周期故障率评估[J]. 电力系统保护与控制，2012，40(1)：85-90.

[4]潘乐真，张焰，俞国勤，等.状态检修决策中的电气设备故障率推算[J].电力自动化设备，2010，30(2)：91-94.

[5]刘若愚.佛山电网输变电设备的状态检修[D].广州：华南理工大学，2014.

[6]胡泽江，刘宗兵，束洪春.基于BP神经网络的设备故障率获取[J].云南水力发电，2008，24(1)：85-88.

[7]杨森，孟晨，王成.基于改进灰色神经网络的故障预测方法研究[J].计算机应用研究，2013，30(12):3625-3628.

[8]刘思峰，谢乃明，党耀国，等. 灰色系统理论及其应用[M].北京：科学出版社，2010.

[9]章伟，邓院昌. 基于灰色-马尔可夫链的短期风速及风电功率预测[J]. 中国电力，2013，46(2)：98-102.

[10]吴文可，文福拴，薛禹胜，等. 基于马尔可夫链的电力系统连锁故障预测[J]. 电力系统自动化，2013，37(5)：29-37.

[11]李小芳，基于改进灰色马尔可夫模型的城市污水量和COD总量预测[D].天津：天津大学，2012.

[12]Moradkhani A, Haghifam M R, Mohammadzadeh M. Failure rate modelling of electric distribution overhead lines considering preventive maintenance [J], Generation Transmission & Distribution IET, 2014, 8(6):1028-1038.

Prediction of the Equipment Failure Rate Based on Improved Grey Markov Model

Li Li1，Xiong Wei2，He Jie2，Yuan Xufeng2，Zou Xiaosong2

(1. Guizhou Institute of Power Equipment Test and Research, Guiyang 550001, China; 2. Electrical Engineering School, Guizhou University, Guiyang 550025, China)

欢迎投稿,欢迎订阅

投稿网址：http://www.dlkxygc.com