频域内海洋资料浮标水动力特性的仿真研究
2016-01-25张继明范秀涛赵强李选群郑珊珊
张继明,范秀涛,赵强,李选群,郑珊珊
(山东省科学院海洋仪器仪表研究所,山东 青岛 266001)
频域内海洋资料浮标水动力特性的仿真研究
张继明,范秀涛,赵强,李选群,郑珊珊
(山东省科学院海洋仪器仪表研究所,山东 青岛266001)
摘要:为研究海洋资料浮标的水动力特性,建立了频域内的运动微分方程,并基于势流理论,仿真了浮标模型在波浪中的运动,与模型水池试验结果进行比较,发现在共振区域内仿真结果的误差较大。为提高仿真精度,利用模型的横摇衰减试验,获得了浮标模型的阻尼系数,并对仿真模型的阻尼矩阵进行修正。修正后的仿真结果与试验结果对比,仿真精度大为提高,平均误差不超过3%,满足工程应用的要求。
关键词:浮标;势流理论;水池试验;横摇阻尼;横摇衰减试验
海洋资料浮标作为海洋观测领域的重要装备,具有连续观测、多参数采集和无人值守等诸多优势。近年来,海洋资料浮标在我国各海域已经大量布放。但是,由于对海洋资料浮标的水动力性能研究不充分,以及对布放海域的水文气象条件考虑不足,浮标倾覆、走锚以及断链等事故时有发生。浮标的水动力性能主要是摇荡特性,对浮标的安全至关重要。因此,亟须对海洋资料浮标的水动力性能开展深入研究。
目前,针对船舶与海洋平台的水动力研究已经很多,而专门对圆盘型结构的资料浮标所做的研究并不多见,但是其理论基础是相同的。随着计算机性能的不断提高,三维势流理论计算海洋结构物的运动得到广泛应用。缪泉明等[1]运用三维势流理论计算了自由浮体的附加质量、阻尼系数以及运动响应,并对极限海况下的三锚系统的浮标运动和锚链受力进行了估算;张炳夫等[2]运用三维势流理论研究了船舶在浅水中的运动和锚系响应问题,并通过转换得到了时域中的水动力参数和波浪力;陈明明等[3]基于波浪辐射/绕射理论,研究了两船在波浪作用下的运动响应特性,给出了相互影响下的附加质量和辐射阻尼,分析了驳船的漂移力和运动响应。王世圣等[4]运用三维水动力模型,对两种不同结构形式的平台在生存状态下的运动特性及波浪载荷进行了分析。王兴刚等[5-6]应用边界元方法和Morison公式对卸载浮标进行水动力分析,应用几何非线性有限元方法计算系泊缆索张力,并在时域内对卸载浮标及其系泊缆索进行了耦合分析。黄昊等[7]以粘性流理论为基础,以连续性方程和N-S方程为控制方程,对Series60船型的二维横剖面绕流进行了数值模拟,计算分析了不同工况下船体剖面的横摇阻尼系数,并与相关实验结果进行了比较。
由于势流理论是基于流体介质为均匀、不可压缩且无粘性的理想流体假设,在仿真过程中忽略了流体的粘性对海洋结构物运动的影响,存在不可避免的误差。因此,为了更准确地计算浮标的水动力性能,必须对三维势流理论的计算阻尼进行修正。本文通过对浮标模型进行水池试验,测得了模型的水动力参数。然后对模型运用三维势流理论进行仿真计算并修正,将仿真结果与试验结果进行对比,研究仿真结果的准确度,为今后海洋资料浮标的水动力计算提供了一种精度更高的仿真方法。
1坐标系与运动方程

图1 浮标运动的坐标系Fig.1 Coordinate of buoy motions
在水动力问题的研究中,浮标一般被看作是具有6个运动自由度的刚体。为便于表示和计算分析浮标在不规则波中的运动响应,采用如图1所示的两个坐标系。总体坐标系O-XYZ,不随浮标或流体运动,OXY平面与静水面重合,OZ轴竖直向上,用该坐标系来表述入射波最为方便;局部坐标系o-xyz,选取与浮标固结、随浮标摇荡的动坐标系,表述浮标运动时,变量将不含时间变量。o点设定在浮标的重心位置,当浮体处于平衡位置时,oxy平面为水平面,oz轴竖直向上。
自由浮标在波浪中受到各种外载荷共同作用引起浮标的运动,包括惯性力、阻尼力、回复力和波浪力。惯性力与浮标的加速度成正比,阻尼力与速度成正比,回复力与位移成正比。浮标在频域内的运动微分方程可表示为
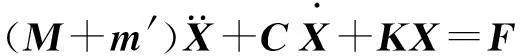
(1)
式中,M为浮标的质量矩阵;m′为浮标的附加质量矩阵;C为系统的阻尼矩阵;K为系统的回复矩阵; X为浮标的运动响应矩阵;F为浮标所受的波浪力矩阵。
考虑几个自由度之间的耦合作用,质量矩阵M可以表示为
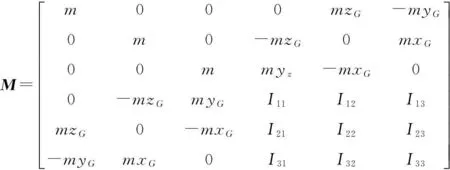
(2)
式中,m为浮标质量;xG、yG、zG为浮标重心坐标;Iij为浮标的惯性矩。
浮标在运动过程中,受到周围水的回复力作用,回复矩阵K可以表示为

(3)
式中,A为浮标的水线面面积;Δ为浮标的排水量;xgb、ygb、zgb为浮标的浮心距重心的距离。
波浪力矩阵F可以根据船级社相关的规范[8]进行计算。至此,为求解浮标的运动方程,只需确定浮标的附加质量矩阵m′和阻尼矩阵C。
2附加质量与阻尼
浮标在波浪力作用下产生运动,其运动的结果将产生一个散射速度势,从而改变速度场的分布,使浮标受到一个附加水动力载荷。由于该载荷与浮标运动的速度和加速度成正比,所以通常以附加质量和阻尼的形式表示。
然而,海洋资料浮标的附加质量和阻尼,只有形状规则的可以得出解析解,而大多浮标的形状是不规则的。这些浮标的附加质量和阻尼只能用数值方法或者水池试验来获得。
本文以浮标的横摇运动为例,根据势流理论,附加质量与阻尼可以表示为

(4)
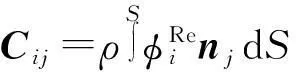
(5)

由于势流理论的局限性, 无法考虑粘性影响和横摇时可能发生的流动分离和漩涡泄出现象, 势流理论方法中的横摇阻尼事实上只计入了兴波阻尼。如果不加修正的话, 横摇运动的预报精度不高, 特别是当外界波浪激励频率接近横摇共振频率时,横摇运动的预报精度缺乏工程实用性。
为此,本文依据浮标的横摇衰减试验对横摇阻尼进行修正。由衰减试验可测得相邻两振幅θk和θk+1的差Δθ=θk-θk+1及平均值θm=(θk+θk+1)/2。以差值Δθ为纵轴、平均值θm为横轴,得到横摇消灭曲线。可以证明,无因次横摇阻尼系数[9]可通过下式计算

(6)
式中,k为横摇消灭曲线的斜率。
求得无因次阻尼系数之后,即可计算浮标的横摇阻尼。将横摇阻尼减掉势流理论计算所得的横摇兴波阻尼,即为需要修正的阻尼值。
3计算结果与试验验证
为了验证运用势流理论仿真结果以及修正阻尼后结果的准确性,本文对一个浮标模型进行水池试验和仿真计算,对比两者的结果。
3.1水池试验
浮标模型水动力特性的试验工作在大连理工大学的试验水池进行,该水池尺度为160 m×7 m×3.7 m(长×宽×水深)。浮标模型试验布置如图2所示。造波机可造规则波和不规则波,所造波浪的频率范围覆盖海洋波浪的主要频率,波高可调。波高由浪高仪测量,浮标升沉值由升沉仪测量,横摇由数字陀螺仪测量,相位差由浪高仪记录的波形和陀螺仪记录的升沉波形所测量。测试采样记录系统,由接口自动将数据输入计算机。

图2 浮标模型试验布置方案Fig.2 Experimental scheme of buoy model
模型缩尺比λ=10,水池试验所采用的波浪周期为0.8~3.7 s,根据换算公式(7)可知,实际波浪周期为2.53~11.70 s。水池水深3.7 m,最大波高0.3 m,根据换算公式(8)可知,实际海水深度为37 m,实际最大波高为3 m。
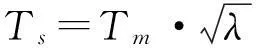
(7)
Ls=Lm·λ。
(8)
3.2仿真计算
仿真模型与试验模型尺寸一致,避免形状误差。仿真水域的深度与试验水池一致,消除了水深对试验和仿真的影响。仿真模型的重量、惯性矩与试验模型完全一致,消除了质量对结果的影响。
仿真模型进行网格划分,划分完后共有11 306个单元,11 308个节点,其中,辐射/衍射单元共5 349个,辐射/衍射节点共5 430个。网格划分结果如图3所示。

图3 仿真模型Fig.3 Simulation model

图4 模型仿真计算Fig.4 Simulation of the model
设置计算波浪周期为0.5~3.7 s,时间步长为0.025 s,波向为沿y轴方向,运用水动力分析软件求解计算见图4。
3.3结果分析
由水池试验测量得到相应波幅下的浮标模型的横摇幅值,横摇幅值除以对应波幅,得到水池试验的单位波幅横摇幅值(RAO)。运用水动力分析软件求解计算,得到仿真模型的RAO。两者之间的对比如图5所示。

图5 修正前RAO结果对比Fig.5 Comparison of RAO results before correction
由图5可见,仿真结果与试验结果在1.7~3.7 s范围内吻合较好,满足工程应用的计算精度;在0.5~1.7 s范围内,仿真值与试验值出现偏差,两者之间RAO峰值相差不大,但是仿真值整个共振区间的峰值出现明显的前移现象。这是因为运用三维势流理论对浮标模型进行仿真时,没有考虑水的粘性,导致横摇阻尼中的粘性阻尼被忽略,从而使得浮标模型的横摇固有周期变小,RAO峰值前移。在浮标模型的横摇固有周期与波浪周期相等时,就会产生共振现象,此时,横摇阻尼中的兴波阻尼会大大增加,而粘性阻尼基本不变,粘性阻尼的影响可以忽略,因此,仿真值与试验值的RAO峰值较为接近。
根据浮标模型的横摇衰减试验(图6)的记录曲线,测得相邻两振幅的差,并进行线性拟合,得到横摇消灭曲线(图7)。
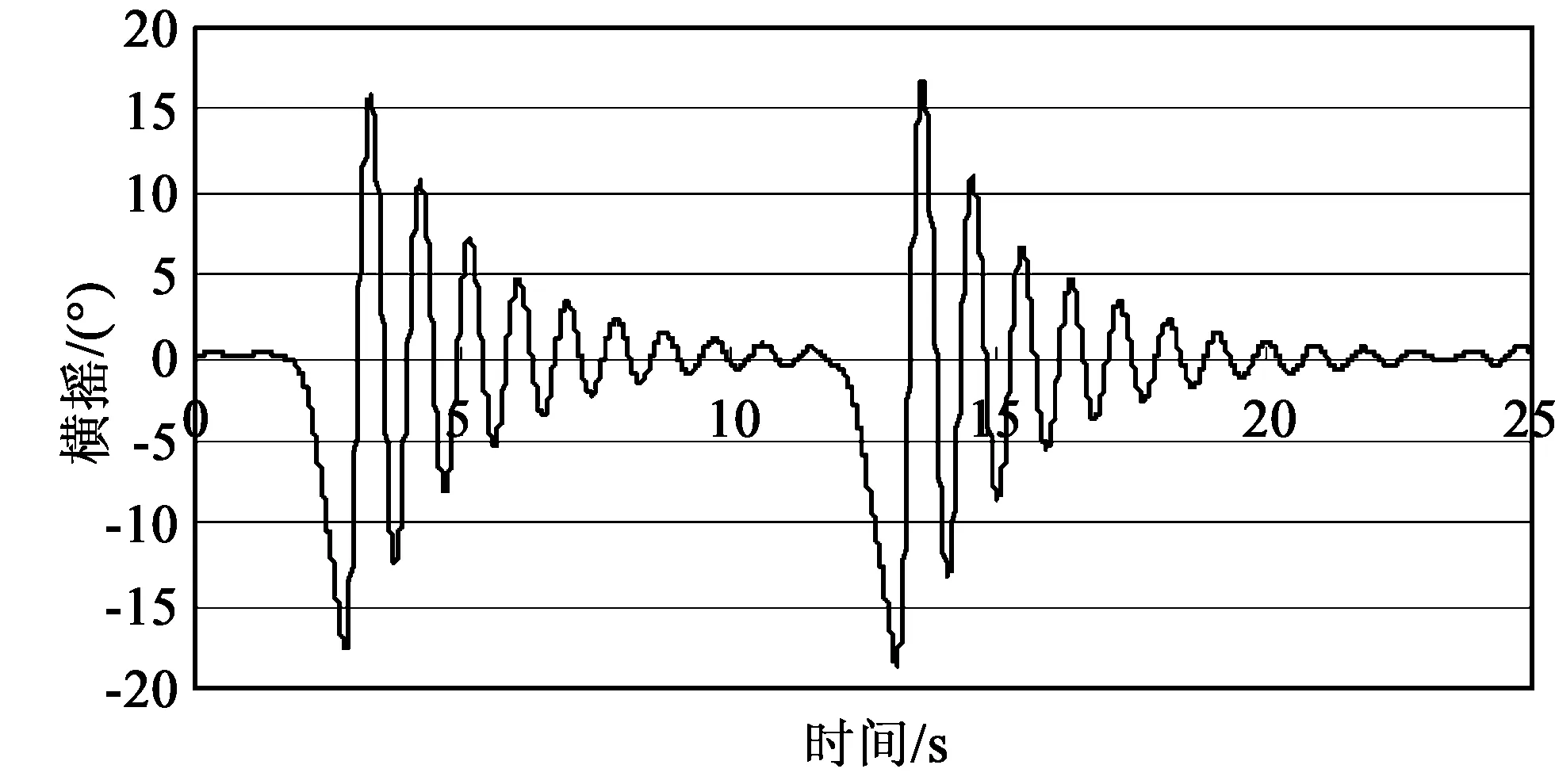
图6 横摇衰减试验Fig.6 Roll decay test
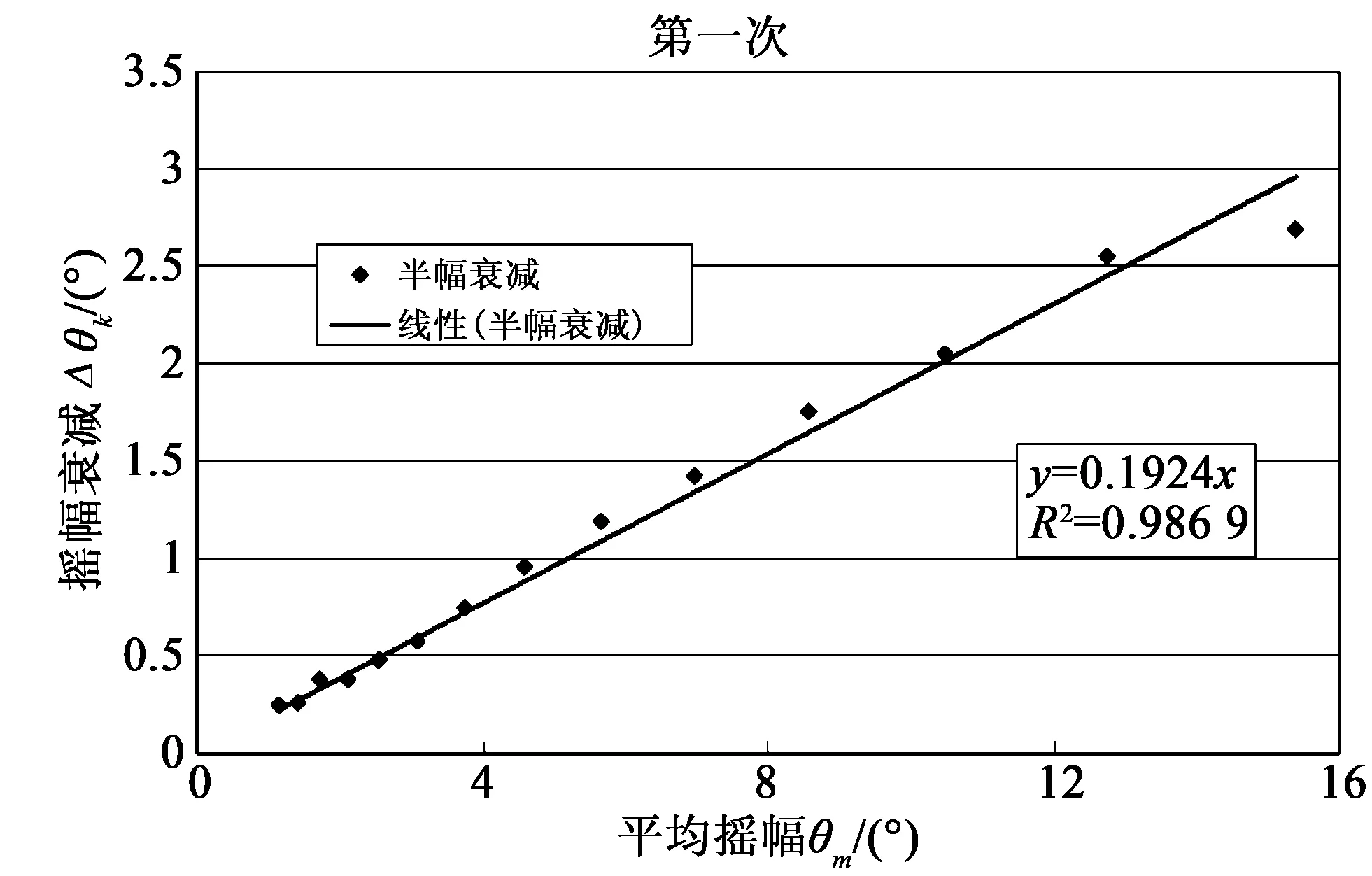
图7 横摇消灭曲线Fig.7 Curve of roll extinction
由横摇消灭曲线的斜率k,计算得到浮标模型的横摇阻尼,对仿真模型的阻尼矩阵进行修正,并添加到仿真设置中,然后重新用水动力分析软件进行求解计算,得到修正后的仿真模型的RAO。修正后的仿真结果与试验结果对比如图8所示。

图8 修正后RAO结果对比Fig.8 RAO results comparison after correction
由图8可见,仿真RAO峰值与试验RAO峰值横坐标基本重合,RAO峰值也相差很小。修正后的仿真结果与试验结果在计算频段内吻合较好,平均误差不超过3%,满足工程应用的精度要求。
4结语
本文建立了浮标在频域内的运动方程,运用三维势流理论仿真浮标在波浪中的运动,并与模型试验的结果进行对比。文中指出求解运动方程的关键是阻尼矩阵的修正,如果不考虑粘性阻尼的影响,仿真结果在共振区域有较大误差。通过利用横摇衰减试验的数据,对横摇阻尼矩阵进行修正,仿真结果可以达到较高的精度,平均误差不超过3%,满足对波浪中浮标运动预报的精度要求。本文对于仿真计算中的阻尼修正,可以大幅提高仿真精度,但是,对阻尼的修正依赖横摇衰减试验数据,后续研究工作可探索运用计算流体力学(CFD)仿真横摇衰减试验,从而用数值仿真代替水池试验,拓宽仿真计算在浮标运动预报领域中的应用范围。
参考文献:
[1] 缪泉明, 顾民, 杨占明, 等.极限海况下浮标运动及锚链受力估算[J].船舶力学, 2003, 7(5): 21-27.
[2] 张炳夫, 钱昆.系泊浮体在浅水波浪中运动响应的计算研究[J].船海工程, 2010, 39(5): 32-35.
[3] 陈明明, 王志东, 杨爽, 等.两船在波浪载荷作用下的运动响应分析[J].中国舰船研究, 2012, 7(2): 24-28.
[4] 王世圣, 谢彬, 冯玮, 等.两种典型深水半潜式钻井平台运动特性和波浪载荷的计算分析[J].中国海上油气, 2008, 20(5): 349-352.
[5] 王兴刚.深海浮式结构物与其系泊缆索的耦合动力分析[D].大连,大连理工大学,2011.
[6] 王兴刚, 孙昭晨, 梁书秀.卸载浮标系统运动响应分析[J].水运工程, 2011 (4): 40-44.
[7] 黄昊, 郭海强, 朱仁传, 等.粘性流中船舶横摇阻尼计算[J].船舶力学, 2008, 12(4): 568-573.
[8] 中国船级社.海上移动平台入级规范[M].北京:人民交通出版社, 2012.
[9] 吴秀恒.船舶操纵性与耐波性[M].2版.北京 :人民交通出版社, 1999.
【海洋科技与装备】
Hydrodynamic characteristics simulation for ocean data
buoy in frequency domain
ZHANG Ji-ming, FAN Xiu-tao, ZHAO Qiang, LI Xuan-qun, ZHENG Shan-shan
(Institute of Oceanographic Instrumentation, Shandong Academy of Sciences, Qingdao 266001, China)
Abstract∶We established a motion differential equation in frequency domain for hydrodynamic characteristics of ocean data buoy.We also simulated buoy modelmotion in wave based on potential flow theory.We discovered a significant simulation result deviation existed, as compared with tank test results.We acquired damping coefficient of a buoy model by roll decay test of the model to improve the accuracy of simulation results.Damping matrix of the model was also corrected.The accuracy of the corrected simulation results was greatly improved, less than 3% of average error, as compared with the experimental results.This can therefore satisfy the requirements of engineering applications.
Key words∶buoy; potential flow theory; tank test; roll damping; roll decay test
中图分类号:P715.2
文献标识码:A
文章编号:1002-4026(2015)04-0008-06
作者简介:张继明(1986-),男,研究实习员,研究方向为海洋结构物水动力分析。Email:jimingzhangwld@163.com
基金项目:青岛市公共领域科技支撑计划(12-1-3-79-jh);国家自然科学基金 (61405106);山东省科学院青年基金(2014QN029)
收稿日期:2015-06-02
DOI:10.3976/j.issn.1002-4026.2015.04.002
