方型柱面贴附置换通风模式影响因素分析

尹海国，李安桂，刘志永，孙翼翔，陈 厅

(西安建筑科技大学环境与市政工程学院，陕西 西安 710055)

建筑室内环境的营造主要采用通风空调系统来实现，系统中合理的气流组织形式既能为建筑空间创造舒适的室内环境、提供较好的空气品质，又能降低空调系统能耗[1-2]．目前通风空调系统采用的气流组织形式主要有基于稀释原理的混合通风和以浮力控制为动力的置换通风[3]．前者存在通风效率较低、卫生条件较差等问题[4-5]；后者能够解决这些问题，但送风直吹人体易造成吹风感，且布置下送风管需提升地面高度，占用工作区有效空间[6-7]．

经过多年的持续性研究，课题组提出了一种基于竖直壁面的新型贴附置换通风模式，能够有效解决混合和置换通风各自的弊端[8-10]．为了将其理念进一步拓展应用，结合建筑空间大中量大面广的柱、廊、杆、条等柱体，充分考虑柱面曲率对贴附送风模式影响下边界层效应的不同，以具有代表性的“方柱”为研究契机，课题组提出了一种基于方型柱面的新型贴附置换通风模式．

1 方型柱面贴附通风模式

方型柱面贴附置换通风模式属于贴附射流的一种，图1为该通风模式气流组织的示意图．空气由位于方柱上部的回形条缝送风口送出后，立即与方柱面形成贴附流动，当流动到地面附近时，在地面逆压梯度的作用下送风主体与方柱面分离，流动方向也由竖直向变为水平向．此后送风贴附于地面并以方柱为中心辐射扩散流动，进而在工作区形成类似于置换通风的空气湖通风模式．由于柱面曲率的影响，导致两个相邻柱面贴附送风进入工作区后存在一定的交汇，因此水平向又可细分为空气湖主流区和空气湖交汇区．

图1 方型柱面贴附置换通风模式原理Fig.1 Principle of square column attached displacement ventilation model

与传统混合通风模式相比，方型柱面贴附置换通风模式能够借助于柱面对送风主体的保持性，将更多新鲜空气和冷/热量分区、均匀下送至工作区，提升通风效率和室内空气品质，且不会出现气流短路情况；而与置换通风相比，风口上置不占用工作区有效空间，且便于布置．同时，借助于建筑空间内均匀分布的柱体，能够解决传统置换通风模式在地铁车站、商场等大空间建筑中难以应用的问题．

2 数值计算模型的建立及实验验证

2.1 物理模型的建立

数值计算用物理模型依据图 1所示房间建立．原型工况房间尺寸为9.0 m×9.0 m×4.0 m（长×宽×高），方柱宽度为1.0 m；送风口采用回形条缝风口，由四个尺寸为1.1 m×0.05 m（长×宽）的条缝风口组成；回风口与送风口位于在同一高度层面，布置在方柱四周，尺寸为0. 2 m×0.2 m（长×宽）．物理模型网格划分如图 2所示，采用结构化网格，经网格独立性验证后，不同计算工况网格数目位于280 ～ 300万之间．为提高计算精度，对送回风口、竖向柱面贴附区、射流冲击偏转区和空气湖区进行了局部加密．

图2 数值计算物理模型网格划分Fig.2 Distribution of grids of numerical computational physics model

2.2 湍流模型选择

采用雷诺平均纳维斯托克斯（Reynolds-Averaged Navier-Stokes, RANS）模拟的方法预测方型柱面贴附置换通风模式的气流组织特性．课题组前期对贴附通风模式模拟常用的十余种湍流模型进行了筛选[11-12]，选择应用较多的重整化群k-ε（Re-Normalization Groupk-ε, RNGk-ε）[13]、可实现k-ε（Realizablek-ε）[14]、剪应力输运k-ω（Shear-Stress Transportk-ω, SSTk-ω）[15]和基于线性压力应变的雷诺应力（Reynolds Stress Model-IP,RSM-IP）[16]共 4个湍流模型进行数值模拟．并用实验数据对各模型的有效性进行验证，以确定适合于方型柱面贴附置换通风模式数值模拟的最佳湍流模型，为该新型通风模式的深入研究奠定基础．

2.3 边界条件设置及求解

本文主要研究条缝风口宽度b为0.05 m时，送风速度、温度，方柱跨度、宽度和回风口位置对方型柱面贴附置换通风模式的影响．因此数值模拟选择3个送风速度（u0=1.0、1.5和2.0 m/s）、3个送风温度（t0=15、17和19 ℃）、3个方柱宽度（d=0.6、0.8和1.0 m）、3个柱子跨度（l=6.0、9.0和12.0 m）和3个回风口位置（回风口到方柱中心水平距离a/柱子跨度l的一半，a/(0.5l)=0.25、0.5和1.0）下方型柱面贴附置换通风模式的气流组织特性．基于前期研究，热源边界条件选择定热流模式，方柱体一般位于建筑内部，贴附送风所承担的外围护结构负荷比例很小，可忽略不计．因此将热流分别设在天花板和地面上（面积均为81 m2），单位面积热流密度分别为20 W/m2（灯光等散热）和80 W/m2（人员设备等散热）．

采用有限体积法（Finite Volume Method, FVM）对物理模型进行离散，采用ANSYS Fluent商业软件进行求解．求解器选用基于压力（Pressure Based）的隐式（Implicit）格式，对流项离散格式采用二阶迎风格式（Second Order Upwind），压力与速度耦合方式采用SIMPLE算法，密度随温度的变化采用Bossinesq假设．计算采用非稳态求解，每次迭代时间步长为3s、每个步长迭代20次，基于对迭代过程典型位置速度及温度的实施监测，确定迭代步数为6 000步．收敛判定标准为计算模型进出口流量不平衡率小于0.2%，P、ui、k、ω项残差均小于10-4，E项残差小于10-6．

2.4 计算模型实验验证

为了验证本文选择湍流模型数值计算的可行性和有效性，采用课题组前期所做的实验数据，给出典型工况下竖向柱面贴附区、空气湖主流区和交汇区数值模拟与实验结果的对比，如图3所示．图中u0表示送风速度，图3a中um(y)表示竖向柱面贴附区房间中截面（z=0）上距送风口y距离处的轴线速度，y方向采用非均匀布点，测试范围为0.15 ～2.25 m；图3b中um(x)表示空气湖主流区房间中截面（z=0）上距冲击角落x距离处的轴线速度，x方向采用均匀布点，测试范围为0.25 ～ 2.35 m；图3c中um(x*)表示空气湖交汇区房间对角线截面上距柱角x*距离处的轴线速度，x*方向采用均匀布点，测试范围为0.35 ～ 3.00 m．

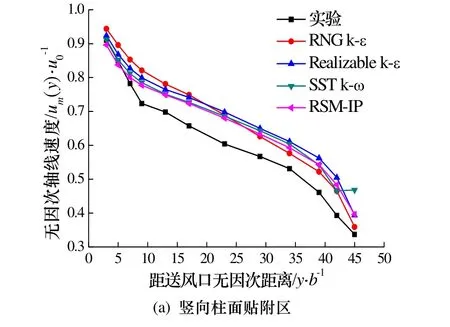
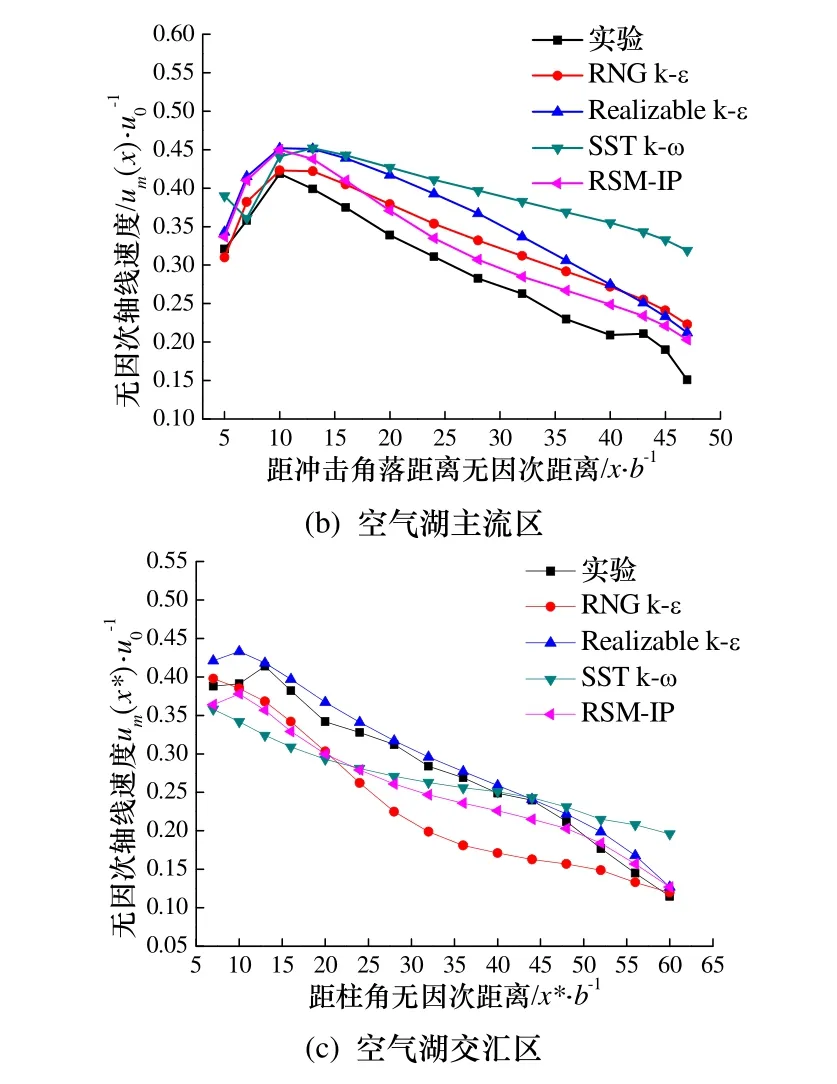
图3 无因次轴线速度计算值与实验值对比图Fig.3 Comparison of non-dimensional maximum velocity with calculated results and experimental data

由图 3a可知，竖向柱面贴附区，四个湍流模型计算得到的模拟结果与实验测试数据的变化趋势几乎一致．准确性方面，不同测点处采用（模拟值-实验值）/模拟值的偏差公式，计算得到RNGk-ε、Realizablek-ε、SSTk-ω和RSM-IP四个湍流模型的预测偏差平均值分别为9.57%、11.06%、10.27%和9.08%，RSM-IP模型模拟准确度最高；空气湖主流区结果与竖向贴附区一致，空气湖交汇区则是Realizablek-ε准确度最高、其次为RSM-IP模型．同时对本文其他工况进行对比，结果得到RSM-IP模型的综合预测性能最优，在竖向柱面贴附区、空气湖主流区和交汇区的平均预测偏差分别为8.96%、10.34%和11.30%．因此，RSM-IP模型能够有效用于方型柱面贴附置换通风模式的数值模拟研究，本文后续部分结果将采用这一模型计算给出．

3 计算结果及分析

3.1 送风速度、温度的影响

针对柱子跨度9.0 m，方柱宽度1.0 m的原型工况，给出不同送风速度、温度下房间中截面（z=0）处速度和温度场分布云图，分别如图4和5所示．

图4 不同送风速度及温度下房间高度方向速度场分布云图Fig. 4 Velocity fields distribution on room height under different supply air velocities and temperatures

图5 不同送风速度及温度下房间高度方向温度场分布云图Fig. 5 Temperature fields distribution on room height under different supply air velocities and temperatures

由图4可知，不同送风速度及温度下送风主体均能沿方柱向下贴附流动，与柱体-地面角落撞击后方向改变，进而沿地面向前扩散流动，在工作区形成类似于置换通风的空气湖状速度分布．送风温度相同时，随着送风速度从1.0 m/s增大到1.5 m/s时，空气湖内对应位置的速度上升了0.1 m/s；而当送风速度从1.5 m/s增大到2.0 m/s时，空气湖的速度场几乎没有变化．当送风速度不变时，送风温度的改变对房间速度场几乎没有影响，说明方型柱面贴附置换通风模式为惯性力主导下的送风．

由图5可知，不同送风速度及温度下方型柱面贴附置换通风模式均能在房间高度方向形成比较明显的温度分层现象，下部人员工作区温度低、上部排风区域温度高，这样的温度分布能够达到较高的通风效率．数值方面，送风速度及温度与室内温度值间存在线性变化关系．送风温度相同时，送风速度每增大 0.5 m/s，房间对应位置温度降低约3 ℃；而送风速度相同时，送风温度每增大2 ℃，房间对应位置温度上升约1 ℃．因此改变送风参数可以实现室内温度的规律性调节，从而满足不同的室内环境参数设计要求．

同时，送风温度对房间温度场分布趋势的影响较小．送风速度相同，不同送风温度下沿房间高度方向的温度梯度近似相同；而送风温度相同时，送风速度越大送风主体与室内空气混合越均匀，沿房间高度方向温度梯度越少，室内温度场越均匀．因此工程设计时，在满足吹风感的前提下应尽量选用较大的送风速度．

方型柱面贴附置换通风模式能够在工作区地面附近形成空气湖，为了分析湖内的速度及温度分布特性，给出地面高度处横截面（y=0.1 m）速度和温度场分布云图．由于送风温度对速度及温度场的影响具有规律性，因此仅对送风温度 15 ℃时，不同送风速度的影响进行分析，如图6所示．

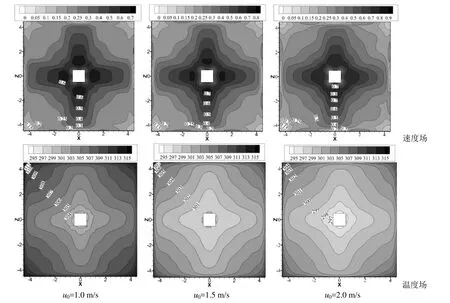
图6 不同送风及温度下空气湖地面高度速度及温度场分布云图Fig. 6 Velocity and temperature fields distribution on air lake under different supply air velocities and temperatures

由图6可知，送风速度的改变同时影响了空气湖内速度大小和速度梯度大小，送风速度越大，空气湖内对应位置的风速越大、速度梯度也越大；送风速度的改变会影响空气湖温度数值，但几乎不会影响温度梯度的分布．同时，空气湖区的流场出现了明显的分区现象，空气湖交汇区的速度、温度梯度总是大于主流区．

3.2 方柱宽度的影响

在原型工况的基础上，研究不同方柱宽度（d=0.6、0.8和1.0 m）对通风模式的影响．由于上一章节分析得到送风速度和温度的影响具有规律性，因此本章节只对送风速度u0=1.5 m/s、温度t0=15 ℃典型工况进行研究．不同截面速度及温差场分布云图如图7和8所示．

由图7可知，方柱宽度在竖向柱面贴附区影响柱面对送风的保持效果，进而决定着送风转向进入工作区后空气湖的速度大小．当柱宽由0.6 m增大到1.0 m时，空气湖速度大小整体上升了约0.1 m/s；温度场方面，方柱宽度的改变对室内温度场分布趋势的影响很小，对房间温度数值的影响较大，方柱宽度每增大0.2 m，房间温度就降低约2 ℃，这主要是因为方柱越宽则送入房间的风量越多、对应冷量越大．

由图8可知，空气湖区方面，方柱宽度直接决定着送风进入主流区和交汇区的比例，方柱宽度越大，则主流区控制的范围越大，柱面曲率的影响也相对减少．

图7 不同方柱宽度下房间高度方向速度及温度场分布云图Fig. 7 Velocity and temperature fields distribution on room height under different square column widths

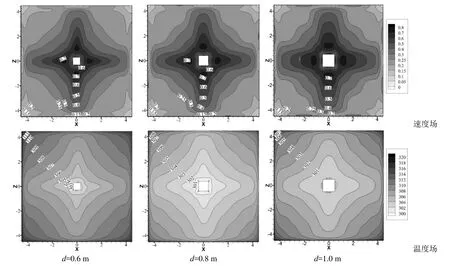
图8 不同方柱宽度下空气湖地面高度速度及温度场分布云图Fig. 8 Velocity and temperature fields distribution on air lake under different square column widths

3.3 柱子跨度的影响

方型柱面贴附射流属于受限射流，柱子跨度对室内流场分布存在一定的影响．图9和10为原型工况的基础上，送风速度u0=1.5 m/s、温度t0=15 ℃的典型工况不同柱子跨度（l= 6.0、9.0和12.0 m）下温度场和速度场的分布云图．

由图9可知，随着柱子跨度的减小，进入空气湖的送风速度变小，空气湖厚度变大，同时送风在柱子对面墙壁上的贴附流动速度也变大，送风有效性降低．因此实际应用时需要根据柱子跨度调整送风速度，柱子跨度较小时应当对应采用较低送风速度；柱子跨度的改变并未影响到房间的竖向温度分层现象，但是柱子跨度越大对应房间温度值越高，同时竖向温度梯度越大，特别是下部工作区．工程设计时应当随着柱体跨度的增加而选择较高送风速度和较低送风温度，以应对室内较大的负荷．

由图 10可知，柱子跨度的改变不影响空气湖区流场的分布趋势，但是柱子跨度越大空气湖水平向速度梯度越大，空气湖主流区和交汇区的分界线也越来越明显．同时，柱子跨度对空气湖温度梯度有很大影响，跨度越大水平向温度梯度越大，这将影响室内人员的热舒适性．总之，方柱面贴附送风模式所能应对的柱子跨度是有限的，本文研究范围内该通风模式所能适用的最大柱子跨度为9.0 m．

3.4 回风口位置的影响

回风口位置是影响气流组织特性的一个因素，在原型工况基础上，研究回风口距方柱中心由近及远，即a/(0.5l)=0.25、0.5和1.0时对通风模式的影响．图11和12为送风速度u0=1.5 m/s、温度t0=15 ℃典型工况下不同截面的速度及温差场分布云图．

图9 不同柱子跨度下房间高度方向速度及温度场分布云图Fig. 9 Velocity and temperature fields distribution on room height under different column spans

图10 不同柱子跨度下空气湖地面高度速度及温度场分布云图Fig. 10 Velocity and temperature fields distribution on air lake under different column spans

图11 回风口位置不同时房间高度方向速度及温度场分布云图Fig. 11 Velocity and temperature fields distribution on room height under different air outlet locations

图12 回风口位置不同时空气湖地面高度速度及温度场分布云图Fig. 12 Velocity and temperature fields distribution on air lake under different air outlet locations

由图11和12可知，回风口位置的改变对房间高度方向速度场几乎没有影响，对温度场的影响也可以忽略不计．对于空气湖区域来说，速度场和温度场也没有发生显著变化．因此，工程设计时可以根据实际需要，回风口在房间上部灵活布置．

4 结语

采用数值模拟的方法对方型柱面贴附置换通风模式送风原理和影响气流组织特性的主要因素进行了研究与分析，得到以下结论：

(1) 方型柱面贴附置换通风模式兼具混合通风和置换通风的优点，能够应用于办公类建筑，以及地铁车站、商场等存在量大面广结构柱体场合大空间建筑的通风空调系统之中．

(2) 送风速度和温度对通风模式的影响主要在室内速度和温度场的数值上，而对流场形式影响较小．通过合理的送风参数设置，可以满足不同的室内环境参数设计要求．

(3) 方柱宽度和柱子跨度对方型柱面贴附置换通风模式的影响也具有规律性，室内环境参数可通过送风速度和温度来调节．柱体跨度小于9.0 m时，方柱宽度越大，通风效果越好．

(4) 回风口位置对该通风模式影响可忽略，工程应用时可根据安装需求来布置回风口．

References

[1] ETHERIDGE D, SANDBERG M. Building Ventilation:Theory and Measurement[M]. New York: Wiley, 1996.

[2] AWBI H B. Ventilation of buildings[M]. London: Taylor and Francis, 2003.

[3] ASHRAE. 2001 ASHRAE Handbook: Fundamentals[M].Atlanta: American Society of Heating, Refrigeration and Air-Conditioning Engineers, Inc., 2001: 26.2-26.3.

[4] SEPPÄNEN O. Ventilation strategies for good indoor air quality and energy efficiency[J]. International Journal of Ventilation, 2008, 6(4):297-306.

[5] LIN Z, CHOW T T, FONG K F, et al. Comparison of performances of displacement and mixing ventilations.Part II: indoor air quality[J]. International Journal of Refrigeration, 2005, 28(2): 288-305.

[6] YUAN X, CHEN Q, GLICKSMAN L R. Performance evaluation and design guidelines for displacement ventilation[J]. ASHRAE Transactions, 1999, 105(1):298-309.

[7] CHEONG K W D, YU W J, SEKHAR S C, et al. Local thermal sensation and comfort study in a field environment chamber served by displacement ventilation system in the tropics[J]. Building and Environment, 2007,42(2): 525-533.

[8] 李安桂, 邱少辉, 王国栋. 竖壁贴附射流空气湖模式通风系统[P]. 中国, 200810017349.0, 2008-01-21 LI Angui, QIU Shaohui, WANG Guodong. A downward directed vertical wall jet ventilation system based on air lake model[P]. P.R. China, 200810017349.0, 2008-01-21.

[9] LI Angui, YIN Haiguo, ZHANG Wangda. A novel air distribution method - Principles of air curtain ventilation[J]. International Journal of Ventilation, 2012,10 (4): 383-390.

[10] 尹海国, 李安桂. 竖直壁面贴附式送风模式气流组织特性研究[J]. 西安建筑科技大学学报（自然科学版）,2015, 47(6): 879-884.YIN Haiguo, LI Angui. Study on airflow characteristics of attached air curtain ventilation model[J]. Journal of Xi'an University of Architecture & Technology (Natural Science Edition), 2015, 47(6): 879-884.

[11] LI Y, NIELSEN P V. CFD and ventilation research[J].Indoor Air, 2011, 21(6): 442-453.

[12] ZHAI Z, ZHANG Z, ZHANG W, et al. Evaluation of various turbulence models in predicting airflow and turbulence in enclosed environments by CFD: Part-1:summary of prevent turbulence models[J]. HVAC&R Research, 2007, 13(6): 853-870.

[13] YAKHOT V, ORSZAG S A. Renormalization group analysis of turbulence. I. Basic theory[J]. Journal of Scientific Computing, 1986, 1(1): 3-51.

[14] SHIH T H, LIOU W, SHABBIR A, et al. A new k-ε eddy viscosity model for high Reynolds number turbulent flows[J]. Computers and Fluids, 1995, 24(3): 227-238.

[15] MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal,1994, 32(8): 1598-1605.

[16] GIBSON M M, LAUNDER B E. Ground effects on pressure fluctuations in the atmospheric boundary layer[J]. Journal of Fluid Mechanics, 1978, 86(3):491-511.