基于混合算法的大跨度钢管混凝土拱桥正常使用可靠度评估

崔凤坤 ，杜岳涛，徐 岳，邵国涛，张昊男

（1．长安大学公路学院 陕西 西安710064；2．台州学院建筑工程学院 浙江 台州 318000）

钢管混凝土拱桥具有结构轻盈、施工方便、承载能力高等优点，在国内外大跨径桥梁建设中得到了广泛应用．近年来，频发的钢管混凝土拱桥病害使人们意识到，结构几何尺寸、材料参数及外部荷载的变异性，对大跨度钢管混凝土拱桥的安全和使用性能有重要影响．因此，基于可靠度理论对大跨度钢管混凝土拱桥进行评估更为合理[1]．

桥梁结构可靠度评估包括承载能力极限状态和正常使用极限状态两个方面．目前，部分学者对大跨度钢管混凝土拱桥的承载能力(强度和稳定性)可靠度开展了研究．许福友等[2]将钢管混凝土拱桥的拱肋考虑成格构柱，建立了拱肋在稳定性失效模式下的功能函数，采用JC法求解了拱肋5个关键截面的稳定性可靠指标；余大胜[3]利用 ANSYS的结构分析功能，结合中心抽样技术和响应面法对钢管混凝土拱肋的强度可靠度进行了研究；于晓琳等[4]将钢管混凝土拱肋的强度失效简化为串联结构，利用基于均匀设计的改进响应面法对拱肋的体系可靠度进行了分析．遗憾的是，目前的研究均很少涉及钢管混凝土拱桥正常使用极限状态下的可靠度评估．然而，设计经验与工程实践表明，大跨径桥梁的安全冗余度通常很高，在一些情况下，正常使用极限状态对结构设计起控制作用[5-6]．因此，有必要全面的对大跨径钢管混凝土拱桥正常使用极限状态下的可靠度进行研究．

钢管混凝土拱桥正常使用可靠度评估主要存在以下问题：随着桥梁跨径的增大，非线性等问题变得突出，复杂的结构特性导致钢管混凝土拱桥的功能函数无法显式表达，常规的可靠度计算方法无法直接求解[7]；大跨度钢管混凝土拱桥在运营阶段失效模式众多，而传统的可靠度评估模型集中于拱肋构件的单独评估，无法对结构整体特性做出全面准确的评价[8]．因而亟需建立一种适合大跨度钢管混凝土拱桥正常使用极限状态的可靠度评估模型，并寻找与之相匹配的高效、精确可靠度计算方法．

从大跨度钢管混凝土拱桥正常使用极限状态的特点出发，基于《公路钢管混凝土拱桥设计规范》和《钢管混凝土拱桥技术规范》，从挠度和应力两个方面构建钢管混凝土拱桥全桥正常使用极限状态下的可靠度评估模型．将均匀设计优选样本思想融入BP神经网络，结合改进JC法提出适用于这类结构可靠度分析的混合算法．

1 正常使用可靠度评估模型

合理的数学模式是进行精确可靠度评估的前提条件，传统的基于单一构件的评估模型在可靠度分析时可能遗漏其他重要的失效模式，因而无法准确反映结构在指定极限状态下的可靠度水平．为了系统的对大跨度钢管混凝土拱桥的正常使用可靠度进行评估，根据《公路钢管混凝土拱桥设计规范》和《钢管混凝土拱桥技术规范》对结构正常使用极限状态的相关规定，从挠度和应力两个角度构建大跨度钢管混凝土拱桥正常使用极限状态下的构件及体系可靠度评估模型．

1.1 构件挠度可靠度评估模型

大跨度钢管混凝土拱桥应具备抵抗荷载作用下异常变形的能力，《公路钢管混凝土拱桥设计规范》中规定：钢管混凝土主拱在正常使用极限状态下的最大竖向挠度不应大于L/1 000；主梁的最大竖向挠度不应大于 L/800．因此，将主拱及主梁位移超限作为其挠度失效模式，并将规范中规定的挠度限值作为该模式下的失效判定准则，以此建立挠度可靠度评估模型：

式中：uL为正常使用极限状态下钢管混凝土拱桥主拱或纵梁挠度限值；为影响正常使用极限状态挠度的n个随机变量．

1.2 构件应力可靠度评估模型

大跨度钢管混凝土拱桥各类构件在正常使用状态下的应力应控制在一定的限值之内，使其具有一定的安全储备．为了建立各类构件的应力可靠度评估模型，首先通过确定性有限元分析，选择各类构件的受力最不利截面，并将该截面应力超限作为该类构件正常使用极限状态下的应力失效模式，对应的应力可靠度评估模型为：

式中：[]σ为正常使用极限状态下钢管混凝土拱桥各类构件应力限值，详见《公路钢管混凝土拱桥设计规范》和《钢管混凝土拱桥技术规范》；为影响正常使用极限状态应力的n个随机变量．式(1) 中的和式(2) 中的均为高次非线性的隐式功能函数，可通过本文提出混合算法中的BP神经网络拟合得到．

1.3 体系可靠度评估模型

大跨度钢管混凝土拱桥是由多种构件组成的复杂体系，结构失效模式众多．为了对正常使用极限状态下的体系可靠度进行评估，本文根据大跨度钢管混凝土拱桥的结构特点，将其近似简化为串联体系，偏安全地认为任意失效模式的发生均导致结构体系失效．基于上述认识，即可采用经典的PNET法对结构体系在正常使用极限状态下的挠度和应力进行更为全面的可靠度评估．所构建的的系统的大跨度钢管混凝土拱桥正常使用可靠度评估模型如图1所示．

图1 大跨度钢管混凝土拱桥正常使用可靠度评估模型Fig.1 Reliability evaluation model for long-span CFST arch bridges at serviceability limit states

2 可靠度计算的混合算法

大跨度钢管混凝土拱桥正常使用可靠度评估模型中存在以下问题：(1) 结构功能函数隐式，常规的FORM法无法直接求解；(2) 基本随机变量个数众多及结构体系复杂，导致功能函数非线性程度极高；(3) 失效概率较低，Monte Carlo等抽样方法计算代价过大．针对上述问题，本文在现有方法的基础上加以改进，提出了适用于大跨度钢管混凝土拱桥可靠度计算的混合算法．

2.1 混合算法基本原理

混合算法将有限元分析、BP神经网络、均匀设计法及改进 JC法相结合，应用于大跨度钢管混凝土拱桥正常使用极限状态可靠度评估中．

2.1.1 BP神经网络

BP神经网络[9]是一种由输入层、隐含层和输出层组成的前馈神经网络，由一系列神经元构成，单个神经元的数学模型为：

式中：f(x)为传递函数；xj为神经元的输入值；yi为神经元的输出值；mij,iθ为BP神经网络的权值和阈值．

研究证明[10]，在隐含层神经元数目足够的前提下，一个3层BP神经网络能够以任意精度逼近非线性函数．因此，BP神经网络非常适合解决钢管混凝土拱桥这种随机变量多、功能函数非线性程度高且无法显式表达的情况．BP神经网络的拓扑结构如图2所示．

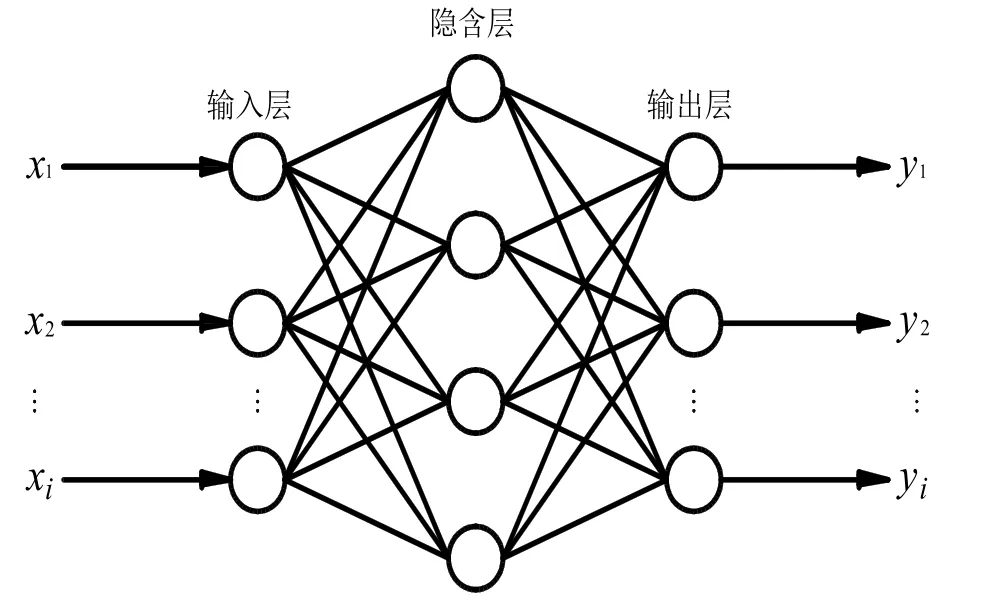
图2 BP神经网络模型Fig.2 BP neural network model

输入样本和输出样本共同组成了用于功能函数拟合的训练样本．在结构可靠度分析中，每组训练样本均需要通过确定性有限元分析获得，而对于钢管混凝土拱桥这种复杂的结构形式，进行有限元分析必然耗费大量的机时．因此，在保证求解精度的前提下，尽量减少样本规模十分必要．采用均匀设计法[11]安排样本数据，相较于正交设计法，样本点具有更好的代表性，从而用较少的样本点取得尽可能充分的结构信息．均匀设计表可通过数理统计系统DPS生成[12]．

2.1.2 改进JC法

通过BP神经网络得到的大跨度钢管混凝土拱桥的功能函数具有高度的非线性，采用传统的 JC法在求解这类功能函数的可靠指标时，经常出现迭代过程不够稳定、最终结果不收敛的情况[13]．研究表明[14]，改进 JC法在求解高次非线性功能函数时具有突出的优势．因此，本文将改进 JC用于大跨度钢管混凝土拱桥可靠指标的求解．

传统JC法在迭代过程中，变量yi的灵敏度系数的计算公式为：

而在改进JC法中，变量yi的灵敏度系数迭代公式为：

通过式(7)和式(8)的比较可知，改进JC法在变量灵敏度系数的计算公式中引入迭代步长λ，克服了传统 JC法迭代过程中更新计算点仅与当前计算点偏导数有关的缺陷，从而可有效调节功能函数非线性程度较高时偏导数的过快摆动，使迭代过程平稳的收敛到曲面上与原点距离最近的点，提高了算法的迭代效率．需要注意的是，通常情况下迭代步长λ取5，当结果不收敛时，可适当增大或减小λ的取值．改进JC法的迭代步骤如下：

(1) 选取迭代步长λ；(2) 选取初始计算点(0)y；(3) 由式(8)计算则结束迭代，否则转入步骤(3)继续计算．

2.2 混合算法分析步骤

基于BP神经网络和改进JC法求解大跨度钢管混凝土拱桥可靠指标的分析步骤如下：

(1) 确定钢管混凝土拱桥可靠度分析随机变量及相应的统计分布，使用均匀设计法优选生成神经网络输入样本；

(2) 根据输入样本建立结构有限元模型，通过确定性有限元分析得到神经网络输出样本(结构变形和应力)；

(3) 对输入和输出样本进行归一化操作，将归一化的样本代入神经网络进行训练，参考文献[15]得到显式化的功能函数；

(4) 通过试算确定迭代步长λ，使用改进JC法求解结构可靠指标．

根据上述分析步骤，编制混合算法程序的详细流程如图3所示．

图3 混合算法计算流程Fig.3 Calculation process of hybrid algorithm

基于混合算法计算流程，综合运用 MATLAB神经网络工具箱、DPS系统的均匀设计功能和ANSYS的APDL语言平台，编制了大跨度钢管混凝土拱桥正常使用可靠度分析程序．

2.3 算例验证

2.3.1 数值算例分析

当功能函数具有显式表达式时，一次二阶矩法应用最为广泛．为了将本文方法的计算精度与一次二阶矩法(作为准确解)进行对比，算例 1选择了一个具有明确解析式、非线性程度较高的功能函数，表达式为：其中X1，X2为基本随机变量，X1～N(10，2)，X2～N(2.5，0.375)．

2.3.2 拱式结构算例分析

算例2为一下承式拱式结构，立面布置如图4所示．计算跨径为10 m，计算矢跨比为1/4，拱轴线采用二次抛物线，拱肋、主梁之间均匀布设8根吊杆，吊杆间距为1.11 m，主梁跨中受到一集中荷载P的作用．

图4 拱式结构立面布置/mFig.4 Elevation of arch structure/m

取结构的随机变量为各构件的截面面积Ai、主梁惯性矩I和施加的外荷载P，相应的统计参数见表1．

表1 随机变量统计参数Tab.1 Statistical parameters of random variables

在正常使用极限状态条件下，主梁允许的最大竖向位移[u]=L/1000=0.01m(L为计算跨径),由此建立结构的极限状态函数为

该算例的输入样本选为100个，由于求解过程与算例1相同，此处不再赘述，仅列出本文方法与其他方法的计算结果，见表2．

表2 算例2可靠指标计算结果Tab.2 Reliability index results of example 2

由于蒙特卡洛法是目前公认的复杂结构可靠度计算的最精确方法，因此将蒙特卡洛法的计算结果假定为精确解．由表2可知，响应面法的求解误差为3.0%，而本文算法的求解误差仅为0.2%，表明本文算法的求解精度高于响应面法；与蒙特卡洛法相比，蒙特卡洛法的计算样本为 105，而本文算法仅采用 100个样本即可得到较为精确的计算结果，进一步说明本文算法在不损失精度的前提下具有更强的实用价值．

3 实桥应用及分析

3.1 工程概况

实桥工程为某中承式钢管混凝土拱桥，计算跨径240 m，计算矢跨比1/4，拱轴线采用悬链线，拱轴系数为 1.5．单幅桥采用双片式拱肋，主拱为等截面钢管混凝土桁架式结构，高 5.35 m，宽 2.75 m．主桥吊杆采用OVM.GJ15-15拉索(1 860 MPa钢绞线)，全桥共设 38根吊杆，吊杆纵向间距为 10 m．横梁通过吊杆、立柱与拱肋相连，横梁高度为2.2 m．桥面系采用纵向“T”型行车道梁，车辆荷载等级为公路I级．主桥立面布置如图5所示．

图5 主桥立面布置Fig.5 Elevation of the main bridge

3.2 可靠度评估的随机变量

影响结构正常使用极限状态的随机变量主要包括结构几何尺寸、材料性能及外荷载等[16]．本文根据实桥统计资料，结合《公路工程结构可靠度设计统一标准》及相关文献，确定了用于钢管混凝土拱桥正常使用可靠度分析的 13个随机变量及相应的统计参数，各随机变量的详细信息见表3．

表3 结构主要随机变量基本统计参数Tab.3 Statistical parameters of main random variables of structure

3.3 有限元建模

使用有限元软件ANSYS建立分析模型，全桥结构离散为3 653个节点和4 258个单元，吊杆采用 link10杆单元，其余构件均采用 beam44梁单元．其中钢管混凝土拱肋采用共线双单元的方式模拟，桁架拱肋与拱座的连接处均采用固结的边界条件．在分析过程中考虑结构几何非线性的影响．

3.4 计算过程及结果分析

结构可靠度分析共涉及到 13个随机变量，使用DPS数据处理系统构造均匀设计表，进而生成神经网络的输入样本．通过有限元分析得到输出样本，将归一化的样本代入神经网络进行训练，BP神经网络参数设置见表4．

表4 BP神经网络参数Tab.4 Parameters of BP neural network

参照混合算法计算流程，选择相应的可靠度评估模型分别对该钢管混凝土拱桥正常使用极限状态下的挠度和应力可靠度进行评估，计算结果分别见表5和表6．

表5 结构挠度可靠度评估结果Tab.5 Reliability evaluation results of structural deflection

表6 结构应力可靠度评估结果Tab.6 Reliability evaluation results of structural stress

由表5及表6计算结果可知：

(1) 正常使用极限状态下，该中承式钢管混凝土拱桥主梁挠度超限失效概率为2.45×10-11，大于主拱挠度失效概率 1.63×10-13，但两者均具有较高的可靠度水平，大于《公路工程结构可靠度设计统一标准》中一级延性构件的目标可靠指标4.7．

(2) 在构件应力可靠度方面，该中承式钢管混凝土拱桥主拱的可靠指标为 9.269，远大于其他构件的可靠指标及规范要求，表明主拱的设计偏于保守，在保证安全的前提下可选用更小的截面面积来优化结构．

(3) 横梁和立柱应力可靠度水平较低，对应的可靠指标分别为3.541和3.815，低于一级延性构件的目标可靠指标 4.7，说明符合常规确定性设计要求的构件，其可靠指标不一定满足可靠度设计统一标准的规定．

(4) 吊杆应力可靠指标为5.137，略大于目标可靠指标 4.7，考虑到吊杆容易受到外界环境侵蚀的影响而产生钢筋锈蚀、断丝等病害，可适当提高吊杆的可靠度水平，使其具有更高的安全储备．

(5) 就结构体系可靠度而言，该中承式钢管混凝土拱桥的挠度和应力具有不同的可靠度水平，体系挠度可靠指标大于体系应力可靠指标．因此仅从单一构件及单一层面对结构进行评估，并不能全面反映大跨度钢管混凝土拱桥在正常使用极限状态下的可靠度特性．

4 结论

(1) 基于现有规范构建的大跨度钢管混凝土拱桥正常使用可靠度评估模型，可以识别大跨度钢管混凝土拱桥在正常使用极限状态下的主要失效模式．同时，可以从挠度和应力两个角度系统地分析各种不确定性因素对结构正常使用性能的影响，为结构风险把控和优化设计奠定理论基础．

(2) 混合算法综合了BP神经网络、均匀设计法和改进 JC法的各自优点，解决了复杂结构功能函数无法显式表达和高度非线性的难题．数值算例和实桥工程应用验证了该算法用于大跨度钢管混凝土拱桥可靠度计算的可行性和准确性，为复杂结构的可靠度评估提供了新的思路．

(3) 大跨度钢管混凝土拱桥即使符合传统确定性设计的要求，也不能保证正常使用极限状态下各构件的可靠指标满足可靠度设计标准的规定．本文提出的正常使用极限状态可靠度评估模型和计算方法可作为传统结构设计的有效补充，能够有效地降低过结构运营期间失效的风险．

References

[1] 康海贵, 张晶, 余大胜. 钢管混凝土拱桥可靠度分析[J]. 大连理工大学学报, 2011,51(2): 226-229.KANG Haigui, ZHANG Jing, YU Dasheng. Reliability analysis of concrete-filled steel tubular arch bridge[J].Journal of Dalian University of Technology, 2011,51(2):226-229.

[2] 许福友, 张建仁, 郝海霞. 钢管混凝土拱桥的拱肋稳定性可靠度分析[J]. 长沙交通学院学报, 2004,20(1):6-10.XU Fuyou, ZHANG Jianren, HAO Haixia. Reliability Analysis of the Arch Rib Stability of Concrete Filled Steel Tubular Bridge[J]. Journal of Changsha Communications College, 2004,20 (1): 6-10.

[3] 余大胜. 钢管混凝土拱桥体系可靠度的探索[D]. 大连:大连理工大学,2005.YU Dasheng. The system reliability exploring of cfst bridge[D].Dalian: Dalian University of Technology,2005.

[4] 余晓琳, 颜全胜, 李炳秋, 等. 基于神经网络的钢管混凝土拱桥可靠度计算[J]. 沈阳工业大学学报,2011,33(5): 582-587.YU Xiaolin, YAN Quansheng, LI Bingqiu, et al. Reliability calculation of concrete-filled steel tubular arch bridge based on neural network [J]. Journal of Shenyang University of Technology, 2011,33(5): 582-587.

[5] 刘扬, 鲁乃唯,汪勤用.基于混合算法的大跨度斜拉桥可靠度评估[J].公路交通科, 2014, 31(7): 72-79.LIU Yang, LU Naiwei, WANG Qinyong. Reliability assessment of long-span cable-stayed bridges based on hybrid algorithm[J]. Journal of Highway and Transportation Research and Development, 2014, 31(7): 72-79.

[6] 孙晓燕, 黄承奎. 既有钢筋混凝土桥梁正常使用极限状态可靠度分析[J]. 湖南大学学报(自然科学版),2006,33(4):21-25.SUN Xiaoyan, HUANG Chengkui. Methods of reliability analysis based on serviceability limit states for existing reinforced concrete bridges[J]. Journal of Hunan University(Natural Sciences), 2006,33 (4): 21-25.

[7] 高谦, 吴顺川, 万林海, 等. 土木工程可靠性理论及其应用[M]. 北京: 中国建材工业出版社, 2007.GAO Qian, WU Shunchuan. WAN Linhai et al. Reliability theory of civil engineering and its application[M].Beijing: China Building Materials Press, 2001.

[8] 刘沐宇, 袁卫国. 基于模糊神经网络的大跨度钢管混凝土拱桥安全性评价方法研究[J]. 中国公路学报,2004,17(4):55-58.LIU Muyu, YUAN Weiguo. Research on safety assessment of long-span concrete-filled steel tube arch bridge based on fuzzy-neural network [J]. China Journal of Highway and Transport, 2004,17 (4): 55-58.

[9] 陈善广, 鲍勇. BP神经网络学习算法研究[J]. 应用基础与工程科学学报,1995(4): 437-442.CHEN Shanguang, BAO Yong. Study on the learning algorithm of bp neural network[J]. Journal of Basic Science and Engineering, 1995(4): 437-442.

[10] RUMELHART D.E, HINTON G.E, WILLIAMS R.J.Learning internal representation by error propagation[J].Parallel Distributed Processing, 1984(1): 348-362.

[11] 方开泰, 马长兴. 正交和均匀实验设计[M]. 北京: 科学出版社,2001.FANG Kaitai, MA Changxin. Orthogonal and uniform experimental design[M]. Beijing: Science Press, 2001.

[12] 粟洪. 大跨度悬索桥结构可靠度分析方法研究[D]. 上海: 同济大学, 2009.SU Hong. Study of the research method about the reliability of the long-span suspension bridge[D]. Shanghai:Tongji University, 2009.

[13] 刘扬, 鲁乃唯, 殷新锋. 基于更新支持向量的大跨度斜拉桥体系可靠度分析[J].计算力学学报,2015,32(2):154-159.LIU Yang, LU Naiwei, YIN Xinfeng. System reliability assessment of long-span cable-stayed bridges using an updating support vector algorithm[J]. Chinese Journal of Computational Mechanics, 2015, 32(2):154-159.

[14] 贡金鑫.结构可靠指标求解的一种新的迭代方法[J]. 计算结构力学及其应用, 1995,12(3):369-373.GONG Jinxin. A new algorithm for solving the structural reliability index [J]. Computational Structural Mechanics and Application, 1995,12(3):369-373.

[15] 粟洪, 程进. 神经网络技术在预应力混凝土桥梁可靠度分析中的应用[J]. 结构工程师, 2009,25(2):71-76.SU Hong, CHENG Jin. Application of neural network in reliability analysis of prestressed concrete bridges[J].Structural Engineer, 2009,25(2):71-76.

[16] 赵国藩. 工程结构可靠性理论及应用[M]. 大连: 大连理工大学出版社, 1996.ZHAO Guofan. Structure reliability and its application[M]. Dalian: Dalian University of Technology Press,1996.