重庆市应用技术型大学在校生数学文化素养现状的差异性分析

蔡银英，张　伟

(重庆第二师范学院 数学与信息工程系，重庆 400067)

重庆市应用技术型大学在校生数学文化素养现状的差异性分析

蔡银英，张伟

(重庆第二师范学院 数学与信息工程系，重庆 400067)

摘要：从6个能力水平对重庆市应用技术大学在校生的数学文化素养进行调查分析，水平3在文理科、年级方面都没有显著性的差异，只在性别方面表现出明显的差异；水平4、水平5、水平6在性别方面没有显著性的差异；水平5、水平6在文理科、年级这两个方面有显著性的差异，即有理科学习背景的学生比文科学习背景的学生表现更好；高年级的学生比低年级学生的素养好。

关键词：应用技术型大学；数学文化素养；水平

作者简介：蔡银英(1976- )，女 ，山西人，硕士，副教授，研究方向:数学教育、应用数学；张伟(1966- )，男，重庆万州人，硕士，副教授，研究方向：数学教育、应用数学。

中图分类号：G648

文献标识码：识码：A

文章编号：编号：1008-6390(2015)06-0152-06

最近几年我国提出建设和发展应用技术型大学，为了应用技术型大学的专业教学与专业建设，有必要了解应用技术型大学在校生的数学文化素养现状。因此选取重庆第二师范学院数学与应用数学专业、移动互联网专业一、二、三年级各30名学生，物流管理专业一、二年级各30名学生；重庆科技学院移动互联网专业二、三年级各30名学生，共300名学生作为调查对象。本次调查发放问卷300份，回收有效问卷294份。

此次调查将个体的数学文化素养从低到高分为6个能力水平来进行描述与分析。

水平1：达到水平1的个体，可以解答情景熟悉、显而易见的问题，能够熟练使用计算器等工具。

水平2：达到水平2的个体，可以运用简单的公式、步骤，进行二步推理，并对结果作出字面上的解释；可以从较多参考背景的情景中提炼出相关的信息，会用单一的表征符号。

水平3：达到水平3的个体，能够准确而清晰地执行背景中所描述的步骤，并能选择和应用简单的问题解决策略；能够解释和使用从不同渠道获得的信息表示方法，能够进行简单的推理，并对自己的结果进行解释、交流。

水平4：达到水平4的个体，能够为有约束条件的或者需要作出部分假设的具体情景建立模型，能够选择不同的表达方法将自己的结果与实际问题联系起来；能够灵活地进行思考和推理，并能形成自己独立的看法与主张。

水平5：达到水平5的个体，能够在复杂的情景中提出问题并建立模型，并能确定约束条件和假设；能够比较、选择和评价相应问题的解决策略；能够进行灵活的思考和推理，有条理的表达自己的看法和主张，还可以对自己得到结果进行反思。

水平6：达到水平6的个体，能够对复杂情景的问题进行分析、归纳，并在调查的基础上对复杂情景的问题进行建模；能够将不同的信息资源联系起来，能够进行深奥的思考和推理，能灵活地运用符号、运算及其相互的关系，并在新的情景中形成新的方法和策略；能够准确地表达自己的结论和发现，并对其进行反思和解释，进而优化模型。

调查问卷设计的问题都选自不同的生活背景，分别为分期付款、旅游、广告增长率、立方体、座位选排、积木、网络聊天、最好的电视剧、面积估算、购买汽车10个问题，这10个问题中又有部分小问题。问卷中的问题可以确保数学文化素养6个水平中的每一个都至少含有两个相应的问题。每个小问题都以10分记，针对学生不同的答题结果给出不同的得分；每个水平则以相对应问题的平均得分来记，总分也为10分。因为广告增长率的印刷问题，导致广告增长率问题的答题率、正确率都与同水平的其他问题有较大的差异；与广告增长率问题相同水平至少还有2个问题，所以在分析中不考虑广告增长率问题对各水平的影响。最后将调查所得到的数据输入计算机，用spss软件进行统计分析。

一、各水平的描述性分析

各水平的分值取对应问题的平均分值，根据水平分值将其分为4个层次，从高到低分别为第3、2、1、0层。如果水平分值大于8说明学生的数学文化素养达到这一水平，用层次3表示；分值大于5不超过8，说明学生具有一定这一水平的数学文化素养，用层次2表示；分值大于2不超过5，说明学生初步具有这一水平的数学文化素养，用层次1表示；分值不超过2说明学生没有这一水平的数学文化素养，用层次0表示。

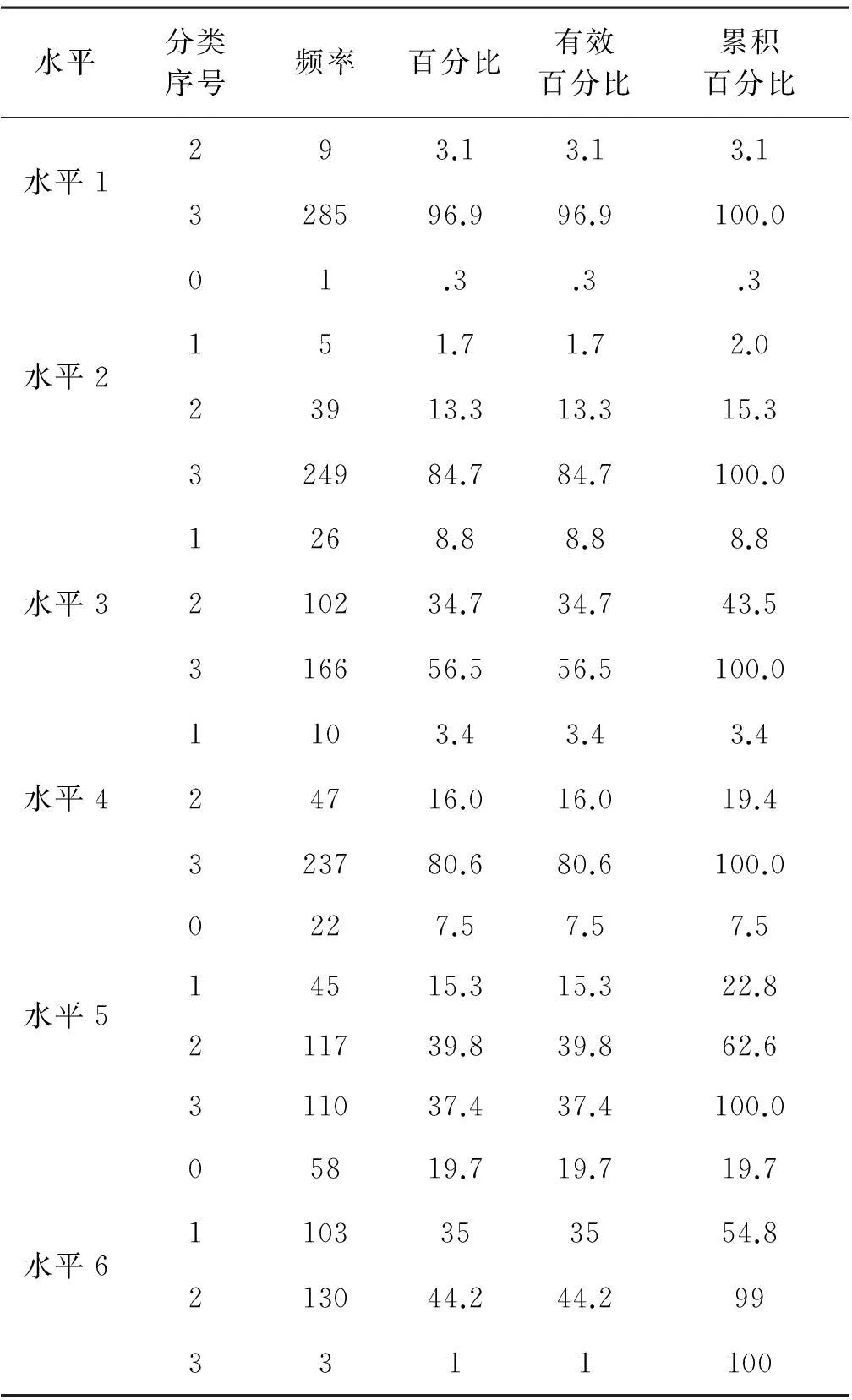
表1-1　各水平层次频率

从表1-1可以看出80%的学生具有水平4的素养,90%以上的学生具有一定的数学文化素养水平4的素养；37.4%的学生具有水平5的素养，7.5%的学生根本不具有水平5的素养；仅有1%的学生具有水平6的素养，19.7%的学生不具有水平6的素养。

从各水平的答题情况及其平均得分可以看出84%的学生的数学文化素养达到水平2，97%的学生有一定的数学文化素养水平2的素养。所以对于数学文化素养的差异讨论只从水平3开始。

二、数学文化素养的性别差异

从表2-1可以看出，男生在各个水平上的平均得分都比女生高，最高差异值为0.45.最小差异值为0.1。

从表2-2可以看出只有水平3的性别差异是显著的，也就是说水平3的男生素养比女生素养高；其余各水平，男女生没有显著的差异，换句话说，男女生的水平素养没有明显的区别。水平3所涉及的三个问题分期付款、积木问题2、网络聊天问题1其背景多是男孩所关注的方向。

三、数学文化素养的文理科差异

从表3-1可以看出文科背景的学生在数学文化素养各个水平上的平均得分都比理科背景的学生低，水平6的差异达到2.3分，超过总分的1/5。

从表3-2可以看出文理科学生在水平3、水平4方面的平均得分虽然有差异，但是从均值检验来看，文理科学生在水平3、水平4方面的差异不显著，也就是说文理科学生在水平3、水平4方面的表现是差不多的。

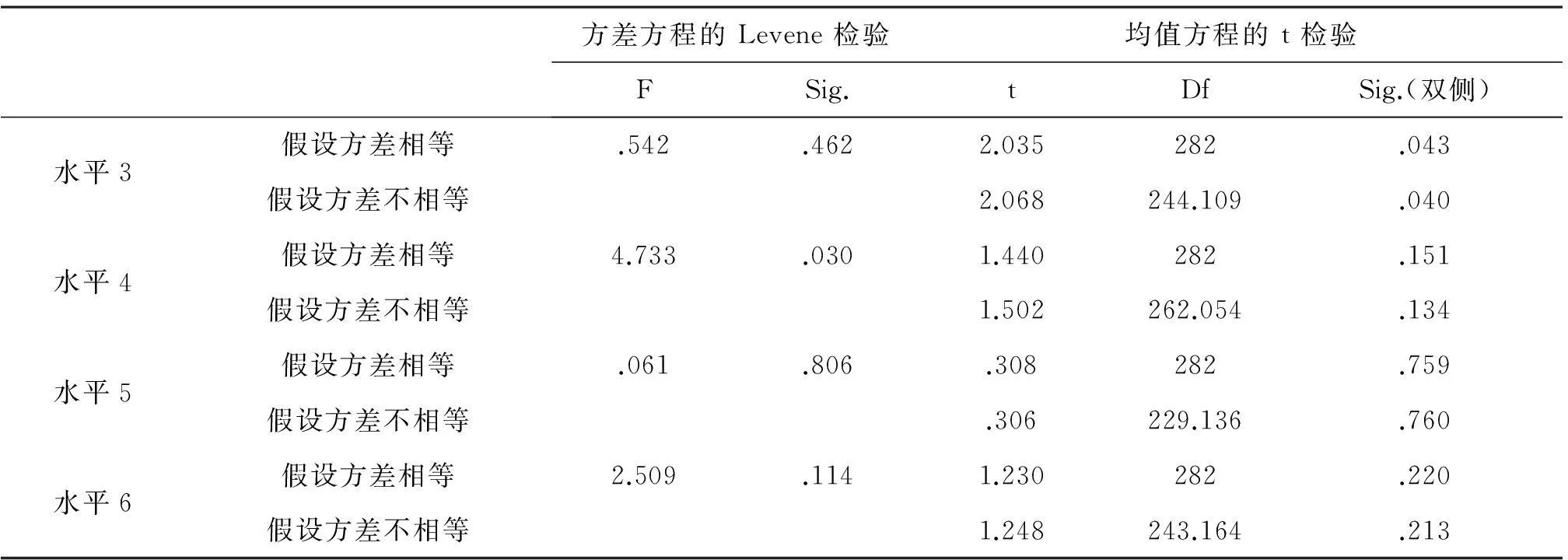
表2-2　各水平的性别差异检验

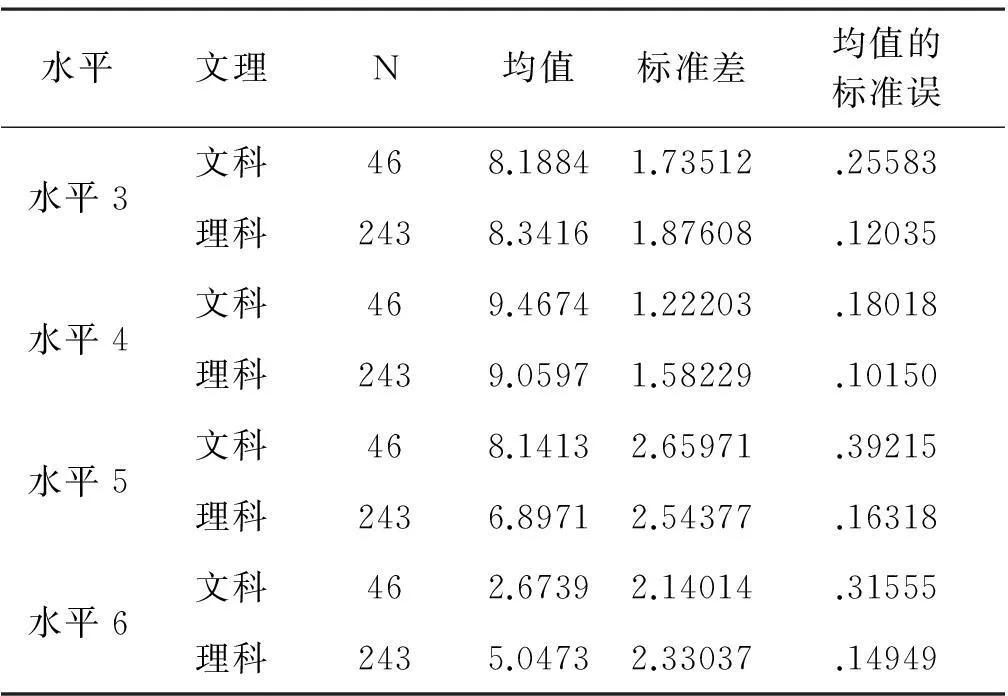
表3-1　各水平的文理科差异列表

文理科学生在水平5、水平6的平均得分是方差齐性的，由均值检验可以看出，文理科学生在水平5、水平6方面的表现有显著的差异，也就是说文理科学生在水平5、水平6方面有明显的不同，理科学生的素养明显高于文科学生。

四、 数学文化素养的年级差异

(一)水平3的年级差异

从表4-1可以看出大三学生的平均得分最高，大一次之，大二最低。最高差值为0.3，最小差值为0.08。

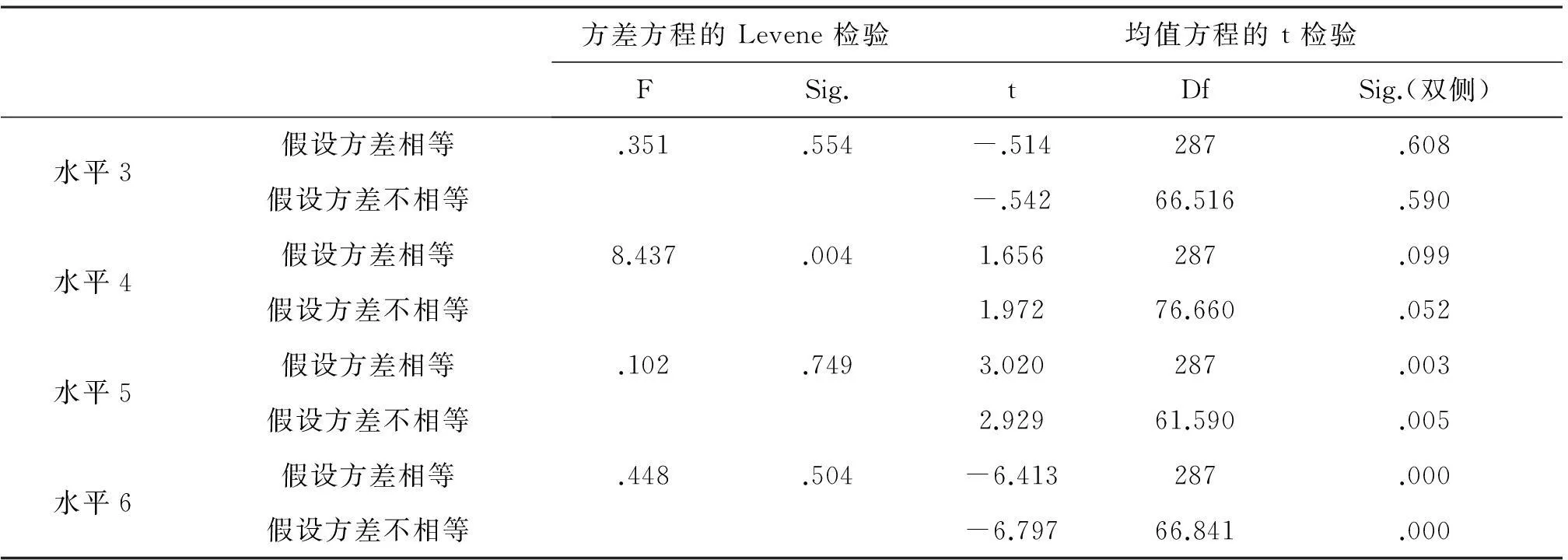
表3-2　各水平文理科差异检验

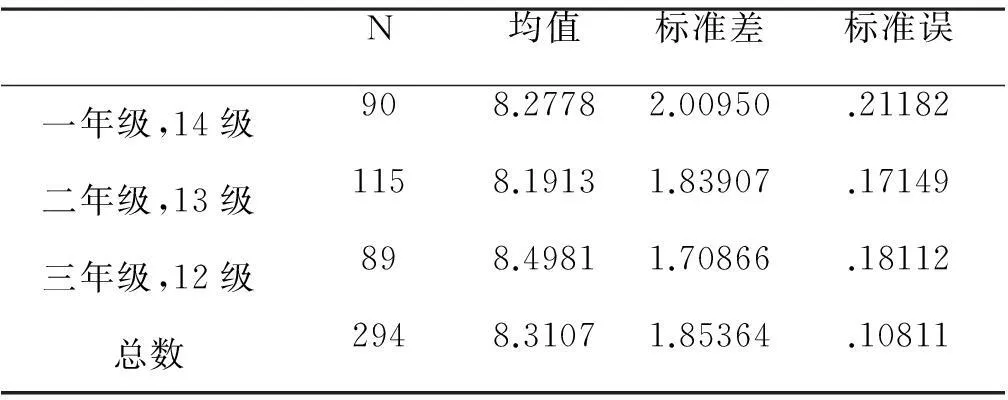
表4-1　水平3的年级差异水平

表4-2.1　水平3年级差异的方差齐性检验

通过对各年级水平3平均得分的单因素方差分析，从表4-2可以看出虽然各年级的平均得分不同，但是一、二、三年级的学生在水平3方面的素养没有明显的区别。

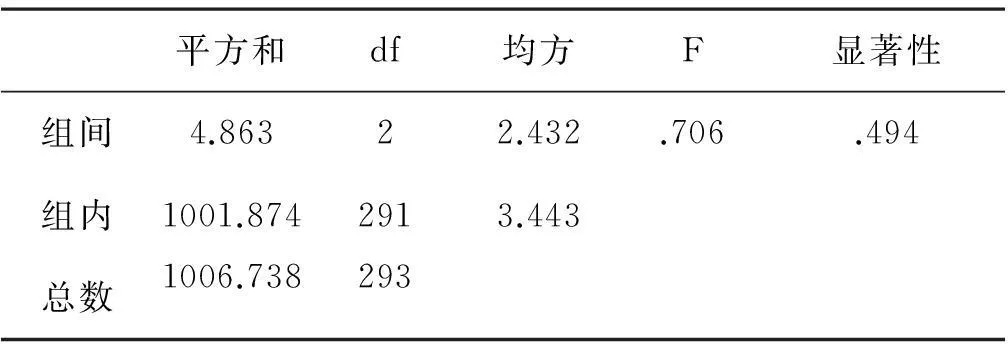
表4-2.2　水平3年级差异的单因素方差分析

从表4-3可以看出这三个年级的中的任意两个年级在水平3方面的素养也没有显著性的差异，也就是说任意两个年级中的学生在水平3方面的表现没有明显的区别。

(二)水平4的年级差异

从表4-4可以看出一年级学生的平均得分最高，三年级次之，二年级最低。最高差值为0.67，最小差值为0.28。

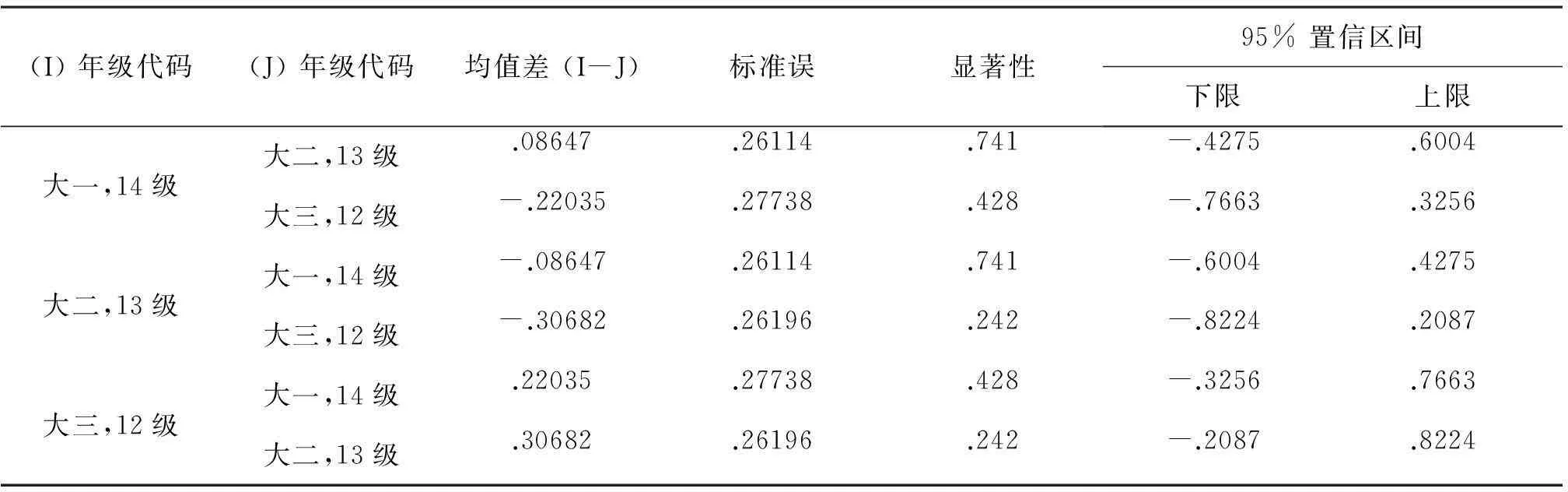
表4-3　水平3年级差异的两两比较

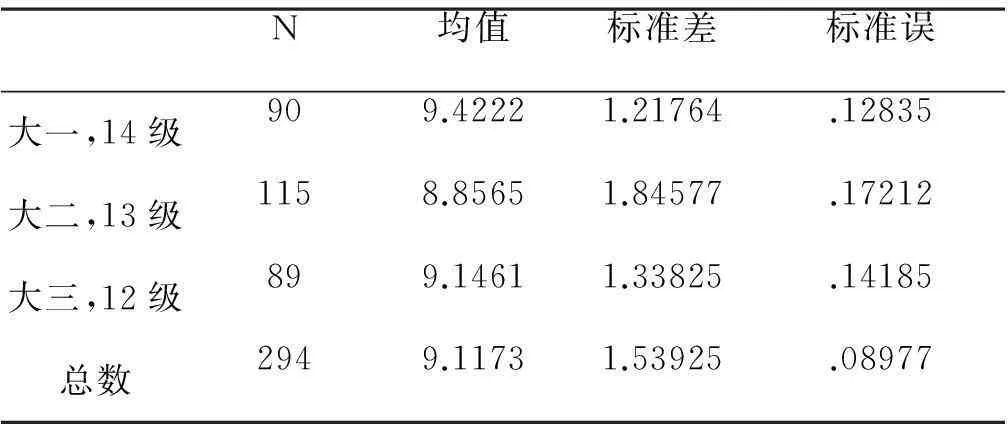
表4-4　水平4的年级差异

表4-5　水平4年级差异的方差齐性检验

对水平4年级差异的方差齐性进行检验，从表4-5发现各年级的平均得分方差有显著性的差异，所以不能对水平4的年级差异进行单因素方差分析。选择独立样本检验对其进行分析。

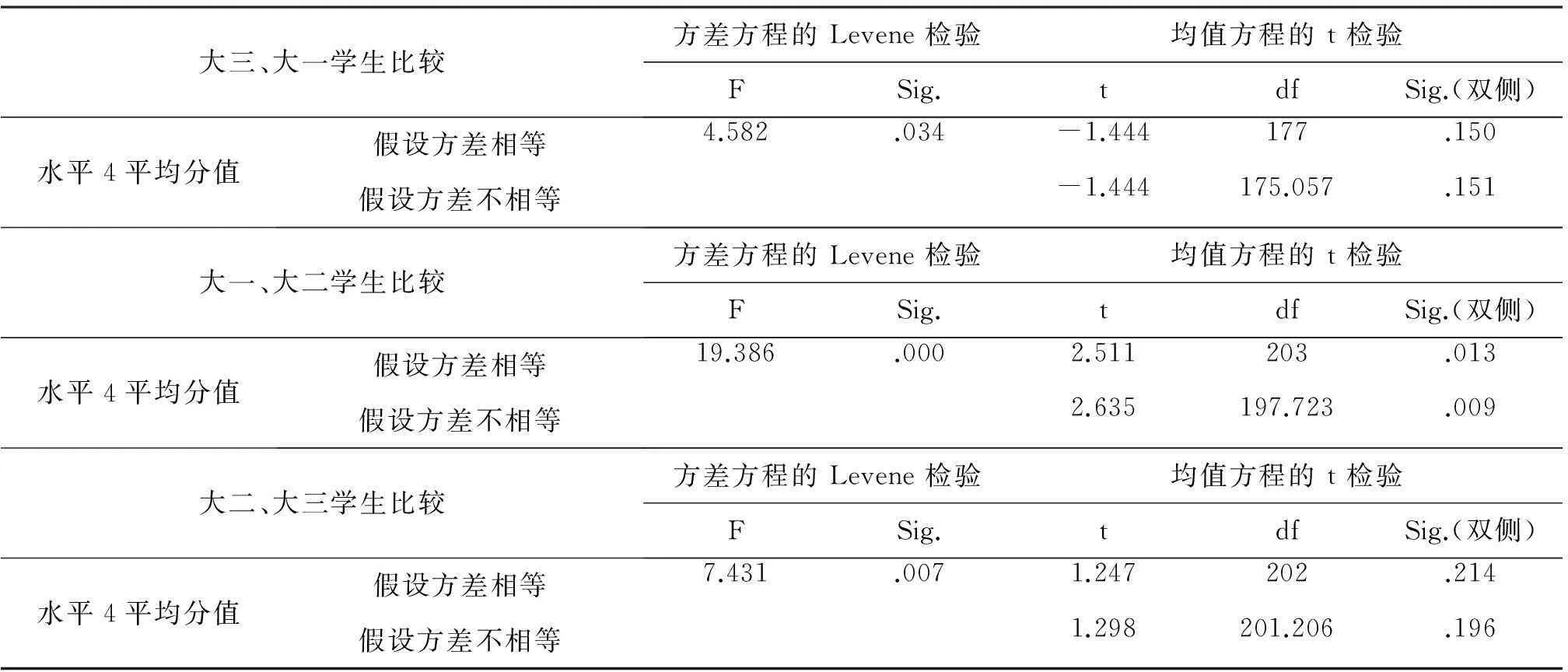
表4-6　水平4年级差异的独立样本检验

通过对水平4年级差异的独立样本检验，从表4-6可以看出一年级与三年级、二年级与三年级的平均得分虽然不同，但是一年级与三年级、二年级与三年级学生在水平4方面的数学文化素养没有明显的不同。一年级学生与二年级学生在水平4方面的表现有显著性的差异，即一年级学生在水平4方面的素养明显高于二年级学生。

(三)水平5的年级差异

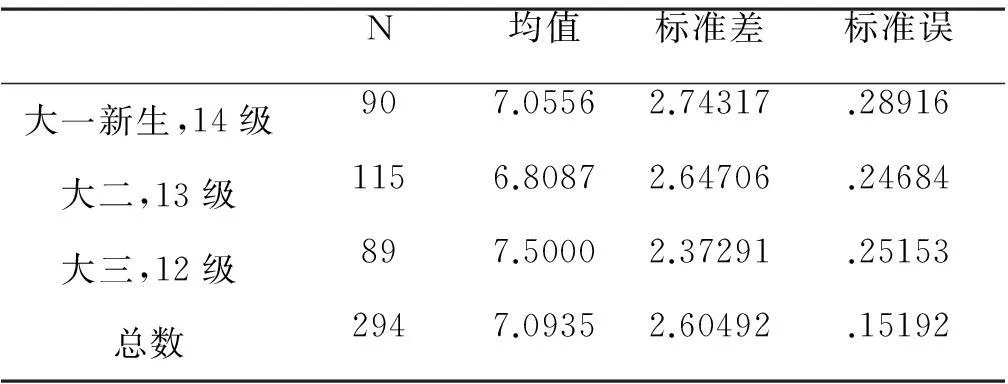
表4-7　水平5的年级差异

从表4-7可以看出三年级学生的平均得分最高，一年级次之，二年级最低。最高差值为0.7，最小差值为0.25。

表4-8.1　水平5年级差异的方差齐性检验

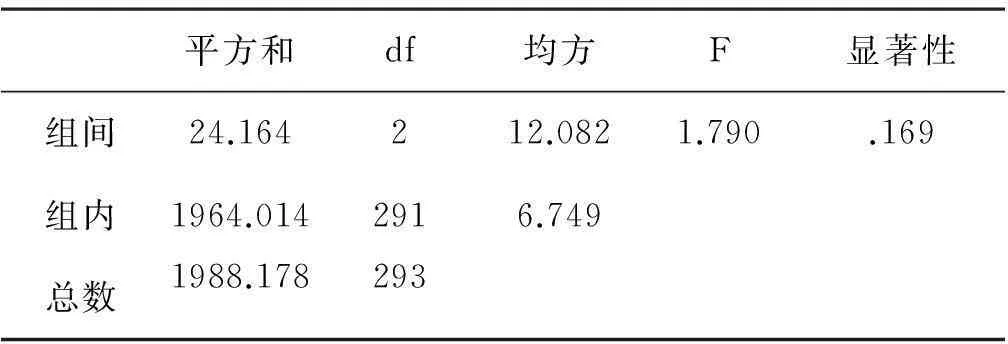
表4-8.2　水平5年级差异的单因素方差分析

通过对各年级水平5的单因素方差分析，从表4-8.2可以看出虽然各年级的平均得分虽然不同，但是一、二、三年级的学生在水平5方面的素养没有明显的区别。

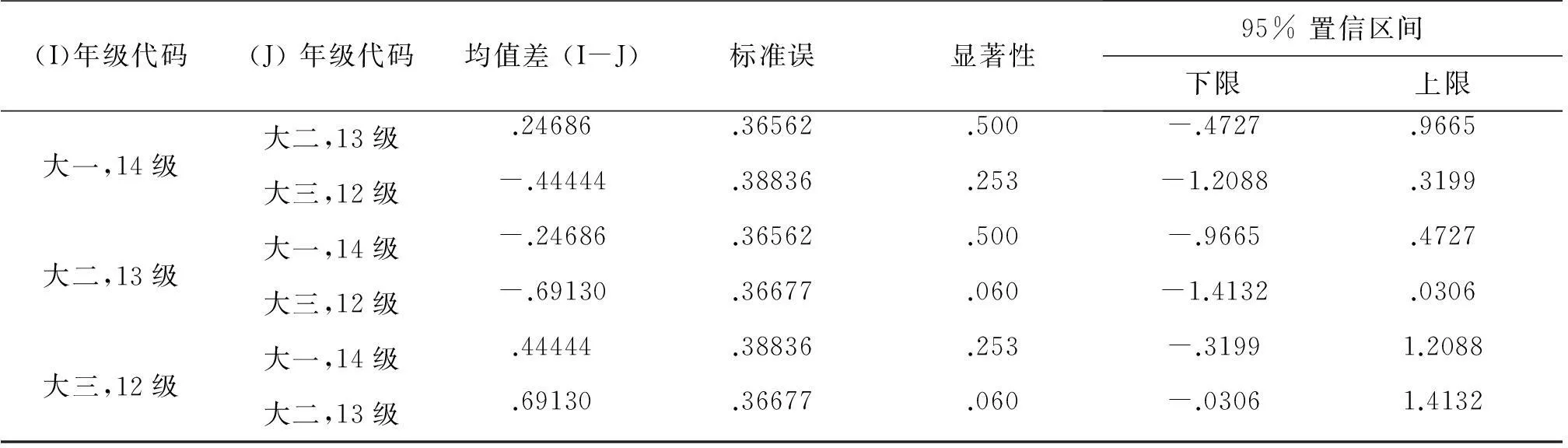
表4-9　水平5年级差异的两两比较

由水平5年级差异的两两比较，从表4-9可以看出这三个年级中的任意两个年级在水平5方面的素养也没有显著性的差异，也就是说任意两个年级中的学生在水平5方面的表现没有明显的区别。

(四)水平6的年级差异

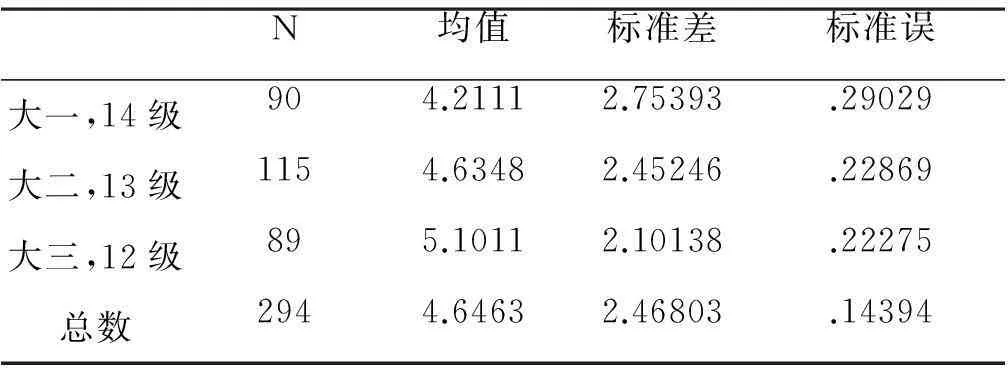
表4-10　水平6的年级差异

从表4-10可以看出三年级学生的平均得分最高，二年级次之，一年级最低。最高差值为0.89，最小差值为0.42。

表4-11　水平6年级差异的方差齐性检验

对水平6年级差异的方差齐性进行检验，从表4-11发现各年级的平均得分方差有显著性的差异，所以不能对水平6的年级差异进行单因素方差分析。选择独立样本检验对其进行分析。

通过对水平6年级差异的独立样本检验，从表4-12可以看出一年级与二年级、二年级与三年级的平均得分虽然不同，但是一年级与二年级、二年级与三年级学生在水平4方面的数学文化素养没有明显的不同。一年级学生与三年级学生在水平6方面的表现有显著性的差异，即一年级学生在水平6方面的素养明显低于三年级学生。

五、结语

重庆市应用技术型大学的大学生的数学文化素养能力：80%的学生具有水平4的素养,37.4%的学生具有水平5的素养，仅有1%的学生具有水平6的素养，7.5%的学生根本不具有水平5的素养，19.7%的学生不具有水平6的素养。

水平3在文理科、年级方面都没有显著性的差异，只在性别方面表现出明显的差异。这与水平3的问题设置有密切的关系。

水平4、水平5、水平6在性别方面没有显著性的差异。水平5、水平6在文理科、年级这两个方面有显著性的差异，一般来说，有理科学习背景的学生比文科学习背景的学生表现更好；高年级的学生比低年级学生的素养好。

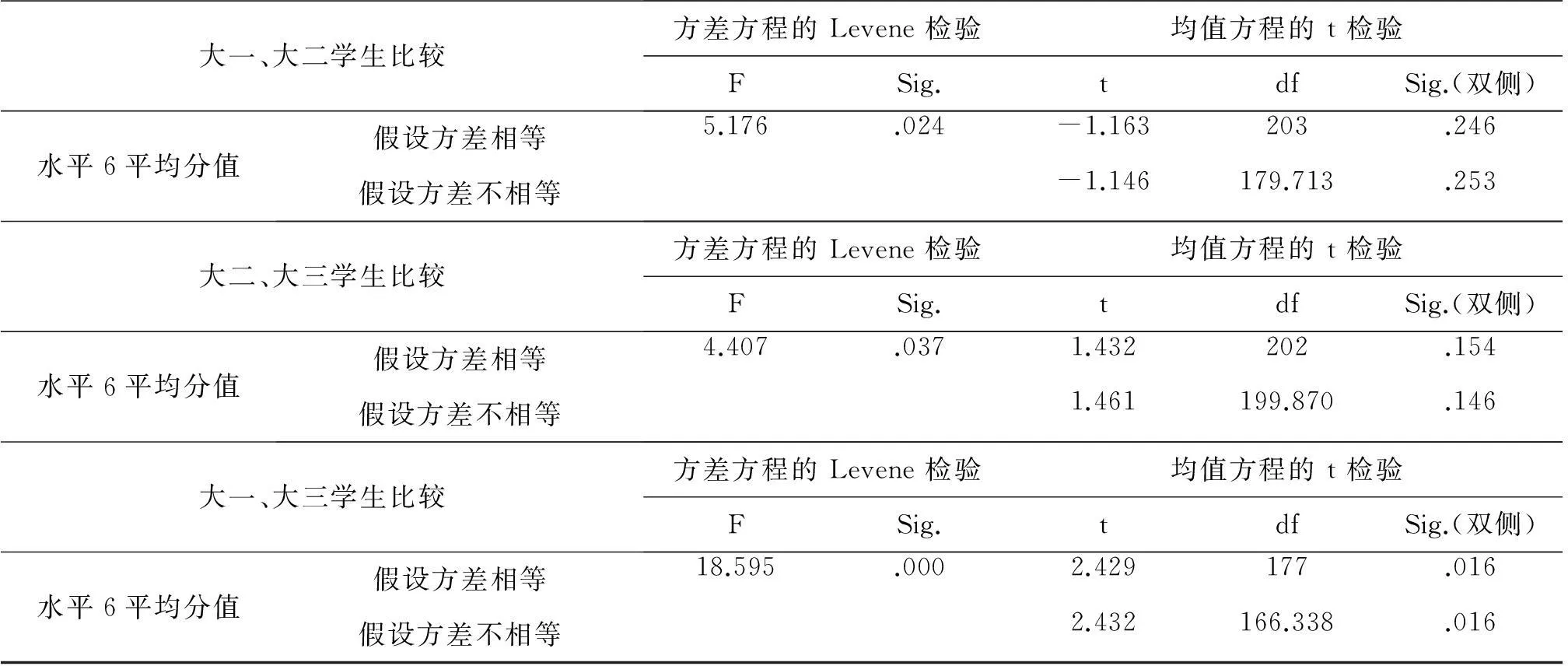
表4-12　水平6年级差异的独立样本检验

参考文献：

[1]康世刚.数学素养生成的教学研究[D].重庆：西南大学硕士学位论文，2009.

[2]王蕾.PISA对学生数学素养的评价[J].数学通报,2009(7).

[3]杨海燕.数学专业大学生数学文化素养的调查研究[D].长春：东北师范大学硕士学位论文，2012.

[4]王璐，王沁.统计软件spss完全学习手册与实战精粹[M].北京：化学工业出版社，2013.

[责任编辑王南山]