一种基于FFT的多谱勒扩频信号捕获方法

高玉平

(中国电子科技集团公司第五十四研究所，河北 石家庄050081)



一种基于FFT的多谱勒扩频信号捕获方法

高玉平

(中国电子科技集团公司第五十四研究所，河北 石家庄050081)

摘要在通信测控系统中短的信号捕获时间是非常重要的。提出了一种基于快速傅里叶变换(FFT)的多谱勒直接序列扩频信号的快速捕获方法，利用频域循环移位特性和FFT变换特点计算出本地伪码序列与输入信号序列的相位差，检测出输入信号多普勒频移。从理论上对该技术进行了研究，分析了捕获方法的基本原理，推导了二维相关计算的数学表达式。用Matlab/Simulink工具进行了仿真,检测出多谱勒频移和伪码相位，进一步验证了该算法捕获的正确性。

关键词直接序列扩频；多谱勒；FFT；频域循环移位。

0引言

直接序列扩频(DSSS)信号直接用伪随机编码序列对载波进行调制，信号隐蔽在噪声中进行通信，能克服多径效应引起的干扰，具有较好的低检测概率和抗截获性能，抗多径能力强，在通信测控领域得到了广泛应用。当扩频信号存在较大的多谱勒频移时，为了缩短捕获时间常采用FFT并行子带捕获方法[1]、部分相关FFT捕获方法[2]和FFT伪码捕获方法[3]。FFT伪码捕获方法利用FFT计算输入信号采样序列与本地伪码序列的互相关函数，检测出伪码相位[4]，用NCO改变本振频率，NCO的变化范围覆盖多谱勒变化范围。NCO每步进一个频点，采集一组数据，进行一次FFT计算；对多组数据进行比较，可以检测出多谱勒的频偏和接收信号伪码相位。部分相关FFT捕获方法，每步近一个伪码相位，进行一次检测，需要遍历所有伪码相位才能完成检测。2种方法都需要较长时间。本文提供一种大多谱勒频移的直接序列扩频信号的检测方法，利用FFT计算检测伪码相位，只需要采集一组数据，通过各种计算，检测出多谱勒频移和伪码相位。

1基于FFT辅助载波调整捕获方法

基于FFT伪码捕获方法主要运用了FFT的方法进行相关，其输出结果为本地码与接收端输入数据的一个相关序列，根据伪码的基本特性，此相关序列存在一个最大值，并且最大值对应接收伪码与本地码的同步。利用FFT伪码捕获方法的原理框图如图1所示[5]。首先将接收数据进行A/D采样、下变频，然后将数据送入FFT单元进行FFT运算，本地伪码也要进行FFT运算，取共轭，然后与接收数据的FFT的结果进行复数相乘，再进行IFFT变换，取出最大值与门限进行比较，若最大值超过门限，则判为捕获成功。

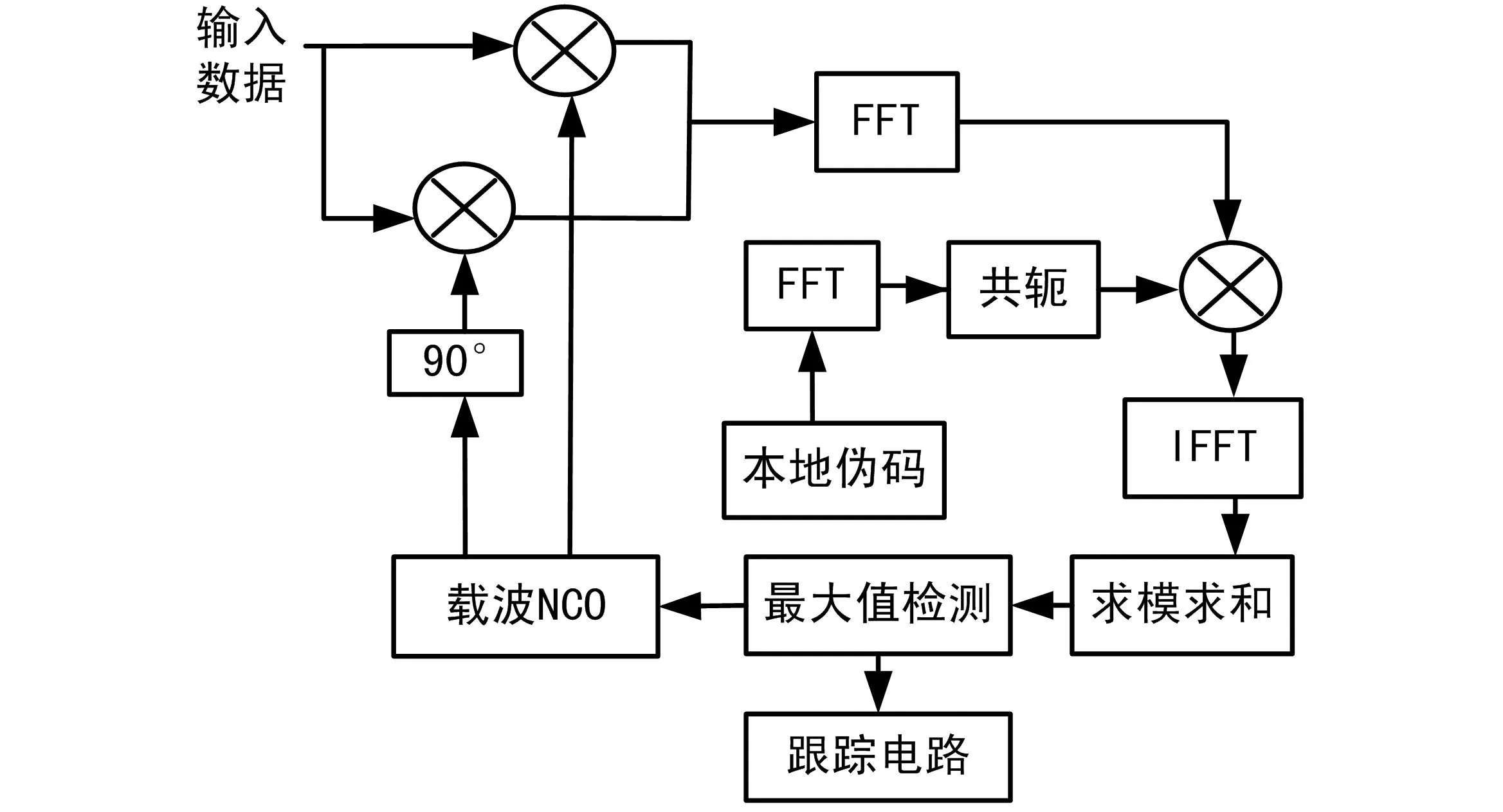
图1　基于FFT与载波调整的扩频信号捕获框图

当存在多普勒频偏时，通过调整本地载波NCO，进行下变频，然后再进行FFT、相乘、IFFT和比较等运算，不断调整，反复运算，可以完成二维的搜索。

设x(n)为输入信号采样序列，y(n)为本地伪码采样序列，序列长度为N，假定输入序列伪码相位与本地序列伪码相位相差m待求。X(k)和Y(k)分别为x(n)和y(n)的N点离散傅里叶变换。本地码序列步进调整，用y(n+m)表示，m的变化范围0～(N-1)，两序列的相关和为[6]：

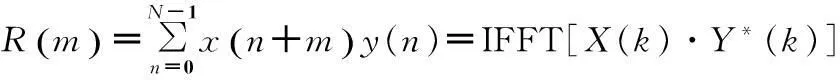
(1)

利用FFT相关定理来实现接收伪码与本地伪码的相关，可直接得到它们的相关序列，根据伪码的基本特性，此相关序列存在一个最大值，并且最大值对应接收伪码与本地码的同步。为了完成多谱勒捕获，需要通过多次调整本地载波NCO，然后进行下变频、采样、FFT、相乘、IFFT和检测等运算，最后完成捕获。

2频域校正的捕获方法

频域校正FFT扩频信号捕获框图如图2所示，与图1不同，没有NCO载波捕获环路。

图2　频域校正的扩频信号捕获框图

与式(1)采用直接进行两序列相关和计算方式不同，采用时域、频域映射的方式进行检测。

本地伪码信号的序列为y(n)，它的FFT序列为Y(k)：

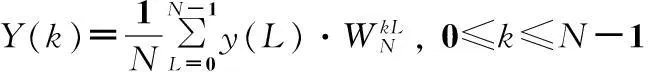
(2)

输入信号经过A/D采集、正交下变频后信号序列为x(n)，它的FFT变换的序列为X(k)：

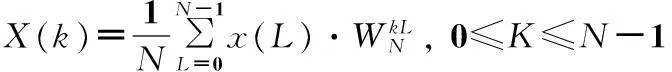
(3)

本地伪码序列对相位进行调整，用y(n+m)表示，m的变化范围0～(N-1)。

时域序列x(n)·y(n+m)的傅里叶变换为[7]：

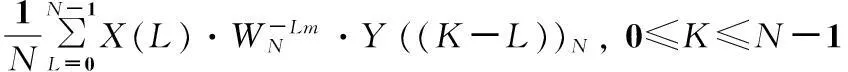
(4)

调整m值，每一个m值，时域序列x(n)·y(n+m)对应一组FFT变换的系数，x(n)·y(n+m)与式(4)一一对应。当y(n+m)与x(n)同步时对应频域FFT的系数有最大值，最大值所在的K值对应多谱勒频率，K在0～(N-1)之间取值。

假定没有多谱勒频率，取K=0，这时式(4)为：

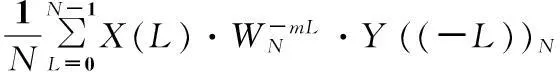
(5)

m在0～(N-1)间取值，这样式(5)等于

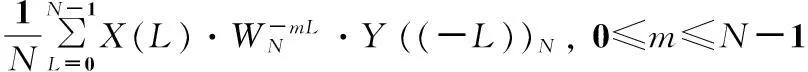
也就是X(L)·Y((-L))N的IFFT变换：

IFFT[X(L)·Y((-L))N]， 0≤m≤N-1。

(6)

当y(n)序列为实数时，Y(-L)=Y*(L)[8]，式(6)等于

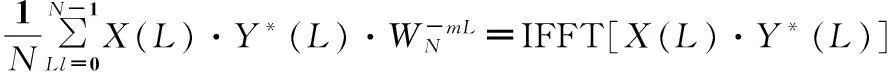
0≤m≤N-1。

(7)

式(7)中，N个数据中最大值对应m值就是输入序列伪码相位与本地序列伪码相位相差m，与式(1)的结果相同。

式(4)中K≠0时，x(n+m)·y(n)的傅里叶变换为：

IFFT[X(L)·Y((K-L))N]， 0≤m≤N-1。

(8)

式(8)是通用表达式，K表示两序列的频率差；m表示两序列的相位差。

式(1)为式(8)K=0的特殊情况，没有谱勒频差。

有多谱勒频偏时，需要进行二维搜索。首先确定最大的多谱勒范围K0，分别取K=0、±1、……±K0按式(8)进行计算，在所有数据中找最大值，最大值对应的K值就是输入信号的多谱勒频偏；所对应的m值就是输入序列与本地序列的伪码相位差。

对Y((-L))N循环移位可以得到Y((K-L))N在K取不同值的序列。

3仿真与验证

用Matlab进行仿真验证式(8)。仿真采用的伪码是63位Gold码补一位“0”，伪码长度64位；伪码周期1 Hz，每个伪码码片有2个采样点，这时采样频率取128 Hz。

本地码的FFT序列输出波形如图3所示。图3(a)为变换后实部序列，图3(b)为虚部序列。实部为共轭对称序列，虚部为共轭非对称序列。

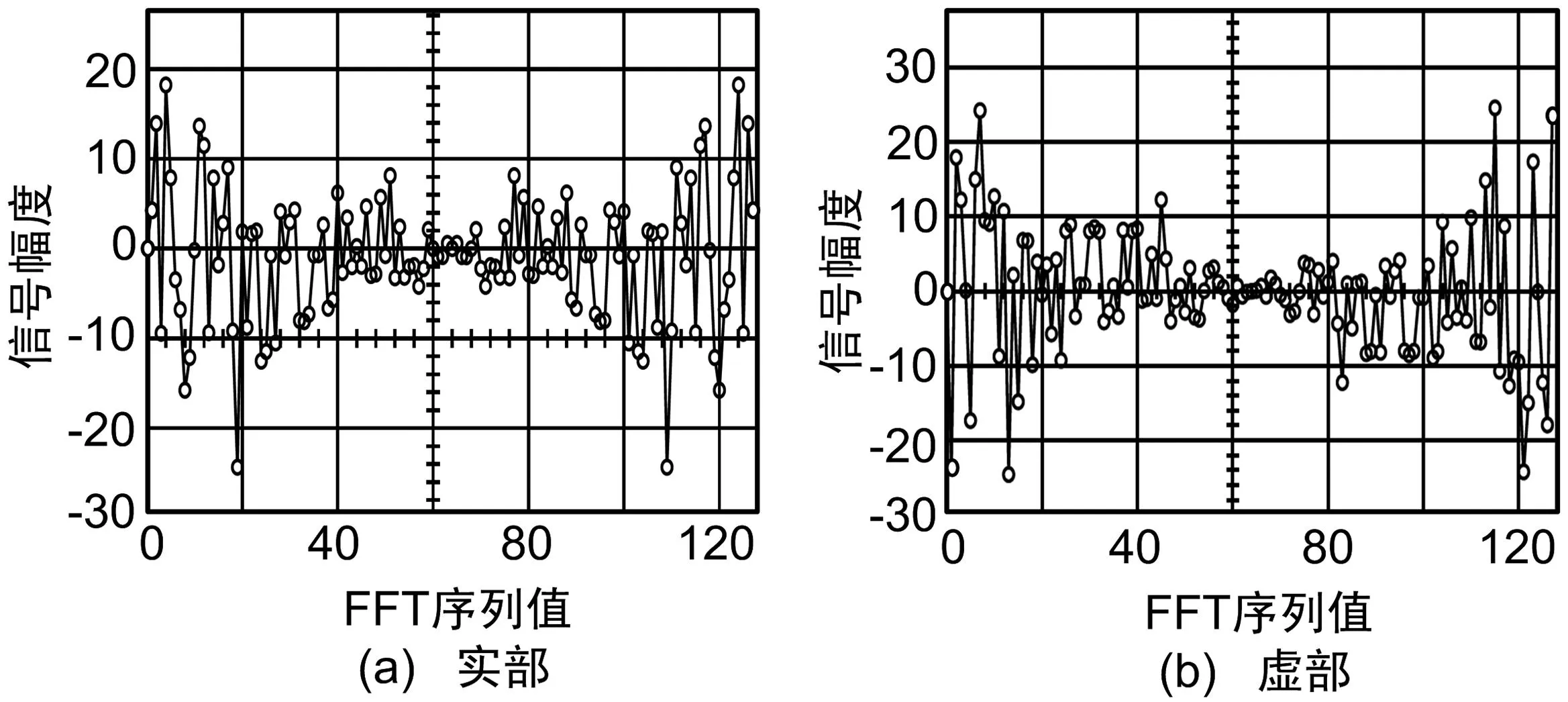
图3　本地码FFT序列

假定输入序列伪码相位与本地伪码相位差20个伪码码片，输入序列多谱勒频移为+16 Hz。输入序列的FFT变换的波形如图4所示。图4(a)为变换后实部序列，图4(b)为虚部序列。

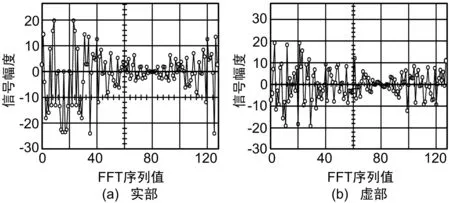
图4　输入数据FFT序列

图3的序列取共轭、移位与图4的序列相乘，然后进行IFFT计算取模输出，输出的相关序列如图5所示。图5(a)中本地码FFT序列共轭后右移28位相关计算的输出，移位对应的频率为14 Hz，因此没有最大相关峰输出。图5(b)是本地码FFT序列共轭后右移32位后进行相关计算的输出，在时间差40的位置，有相关峰最大值输出。这样可以得出输入序列多谱频率16 Hz，与本地码相差20个伪码码片。仅当本地码FFT序列共轭后右移32位时有相关峰输出最大。

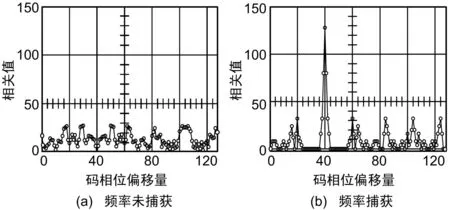
图5　频域相关输出序列

4结束语

伪码相关函数是直接序列扩频信号同步的基础，基于FFT的伪码捕获方法根据时域卷积与频域相乘的关系，利用FFT完成时域的相关计算。当存在多普勒频率时，根据时域同步、频域最大的原则，在频域找出最大值，确定所对应的频率值和码相位偏移量，利用FFT计算实现快速捕获。本文推导的公式经过验证，具有工程实用价值。

参考文献

[1]CHENG U,HURD W J,STATMAN J I.Spread-spectrumCode Acquisition in the Presence of Doppler Shift and Data Modulation[J].IEEE Trans.Commun.,1990,COM-38(1):41-50.

[2]GRANT P M,SPANGENBERG S M,Scott I.DopplerEstimation for Fast Acquisition in Spread Spectrum Communication Systems[C]//Spread Spectrum Techniques and Applications,IEEE 5th International Symposium on,1998:106-110.

[3]ALAQEELI A,STARZYK J,GRAAS F V.Real-time Acquisition and Tracking for GPS Receivers[C]//Circuits and Systems,Proceedings of the 2003 International Symposium on,2006:500-503.

[4]KIDO Ken’iti.Digital Fourier Analysis:Advanced Techniques[M].New York:Springer,2015:28-45.

[5]王伟，徐定杰.基于FFT的伪码快速捕获[J].哈尔滨工程大学学报，2003(10)：646-650.

[6]NEE D J R V,COENEN A J R M.New Fast GPS Code-acquisition Technique Using FFT[C]//Electronics Letters,1991(1):158-160.

[7]奥本海姆A V，谢弗 R W.数字信号处理[M].北京：科学出版社，1981：74-81.

[8]高西全，丁玉美.数字信号处理[M].西安：西安电子科技大学出版社，2001：71-77.

高玉平男，(1963—)，高级工程师。主要研究方向：无人机测控技术。

引用格式：高玉平.一种基于FFT的多普勒扩频信号捕获方法[J].无线电工程,2016,46(1):39-41.

A Doppler Spread Spectrum Signal Acquisition

Algorithm Based on FFT

GAO Yu-ping

(The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China)

AbstractThe short acquisition time is very important for TT&C.This paper describes a fast acquisition algorithm for Doppler direct sequence spread spectrum signals based on fast Fourier transform(FFT).This algorithm uses frequency domain cyclic shift theorem and FFT transform to calculate the phase difference of local PN-code sequences and incoming sequence and estimate the Doppler shifts.This paper analyzes the basic principles of the fast acquisition algorithm and deduces the mathematical expressions of two-dimensional correlation calculation.The simulation is performed with MATLAB/Simulink tools to detect Doppler shifts and PN-cod phase,and the results show that the mathematical expressions of this algorithm are correct.

Key wordsDS-SS;Doppler;FFT;frequency domain cyclic shift

作者简介

基金项目：国家部委基金资助项目。

收稿日期：2015-10-22

中图分类号TN 911.7

文献标识码A

文章编号1003-3106(2016)01-0039-03

doi:10.3969/j.issn.1003-3106.2016.01.09