一种逼近零抖动的Gardner定时误差检测算法

冯彐然，韩　军

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；

2.通信网信息传输与分发技术重点实验室，河北 石家庄 050081)



一种逼近零抖动的Gardner定时误差检测算法

冯彐然1,2，韩军1

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；

2.通信网信息传输与分发技术重点实验室，河北 石家庄 050081)

摘要随着无线通信容量的提升，在频率资源紧张的情况下，为了提高整个系统的频带利用率，实现高速率传输，必须采用高阶调制，低滚降系数成型。但是高阶调制和低滚降系数成型会增大自噪声，造成定时抖动过大，容易引起失步。针对该问题研究了一种适用于高阶调制(MQAM)和低滚降系数成型下的定时同步算法——基于预滤波的Gardner算法，仿真得到加预滤波前后的波形时域图和小数间隔收敛的抖动图，通过仿真可以清晰看到预滤波前后波形的变化及定时抖动的减小。

关键词位定时同步；低滚降系数；MQAM；预滤波；零抖动

0引言

随着通信技术的快速发展，信息传输速率甚至达到了吉比特[1]。但是在频率资源紧张的情况下，只有采用高阶调制、低滚降系数成型，才能提高整个系统的频带利用率，从而实现高速率传输。定时同步作为基本的同步技术，是进行正确抽样判决的基础，因此研究一种适用于高阶调制和低滚降系数成型下的定时同步算法很有必要。

本文通过对经典Gardner算法进行分析，并基于内插数字化实现，针对其应用在低滚降系数成型和高阶QAM调制下自噪声的增大导致定时抖动增大[2]，容易引起失步的问题进行研究，采用对2倍符号率的抽样信号过预滤波的方法，达到了逼近理论零抖动条件(Zero Jitter,ZJ)[3]，提出了一种预滤波[4]实现方法，并给出改进前后的仿真结果。

定时误差检测算法主要包括早迟门算法、Mueller&Mueller算法、Gardner算法及其改进算法、数字滤波平方定时算法等。早迟门算法每个符号需要3个采样点，因此其不适用于处理高数据率的系统中；Mueller&Mueller算法对载波频偏比较敏感；数字滤波平方定时算法应用于低滚降系数成型下性能会下降[4]，因此这里重点研究Gardner算法。该算法中每个符号只需要2个采样点，与载波同步相互独立[5]，同时采用Gardner算法的定时同步环路结构简单，可于载波恢复之前实现，因此Gardner算法被广泛应用[6]。

1Gardner经典算法

Gardner算法原理如图1所示。接收的信号经过匹配滤波，以高于2倍的信号速率进行抽样，利用Gardner 算法进行定时误差检测，估计结果经过环路滤波以减小抖动之后驱动 NCO 产生内插所需的参数，通过立方插值滤波器完成内插，恢复出最佳采样点的数值。

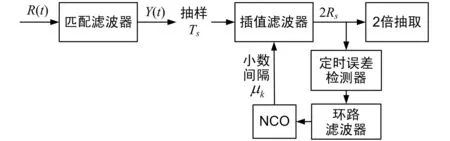
图1　Gardner算法原理

假定τ为偏离最佳采样位置的定时偏差，则Gardner算法产生的符号同步误差序列为：

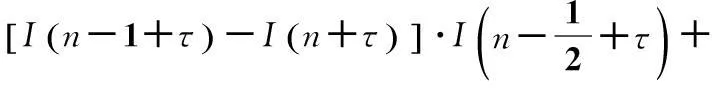
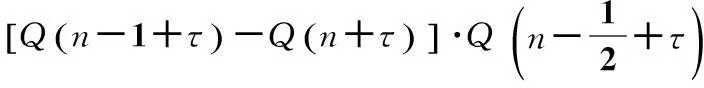
(1)

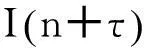
数字环路滤波器的递归表达式为：

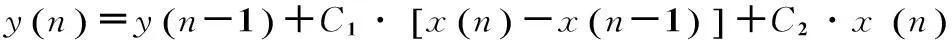
(2)

C1=2(wnξ)/k，

(3)

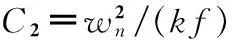
(4)

式中，wn为环路带宽；环路带宽越大，收敛越快，但收敛的精度小；而wn越小，则收敛越慢，收敛精度大。阻尼系数用ξ表示，由模拟锁相环的知识可知[7]，一般取0.707，若想增强环路的抗噪性能，ξ可取0.5。

从环路滤波器的输出得到数控振荡器的步长调整量后，数控振荡器就会以新的步长运行，数控器以步长量为减数做减法，减法操作由时钟控制，当寄存器中的数减到溢出成为负数时，即输出一个控制使能。在溢出的前一刻，寄存器中所保留的数即是需要的分数间隔，这个分数间隔用于插值滤波器计算内插值，为了继续进行减法计数运算，需要对这个负数再加上数字“1”，然后继续以新的步长做减法计数。

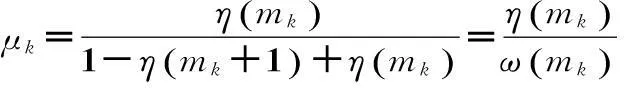
(5)

内插滤波器采用基于多项式的内插滤波器的实现，本文中采用立方内插滤波器[9]，其滤波器的系数为：

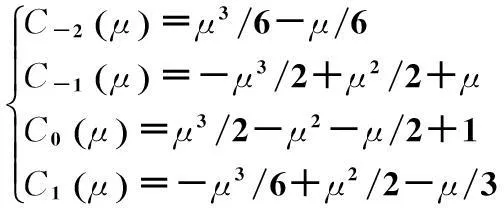
(6)

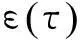
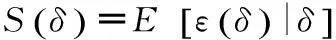
(7)

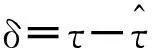
不同滚降系数下S曲线如图2所示，可以发现成型的滚降系数越高，S曲线越接近正弦曲线。对于一个定时误差检测器，其误差灵敏度kd是环路增益的一部分，是后续环路参数计算的先决条件[9]。kd一般取误差检测器的S曲线在零定时误差附近的斜率。由图2可以看出，随着滚降系数减小，kd也会越来越小，直到不能够对定时误差进行有效的检测。所以原始Gardner算法无法在滚降系数取值较小的情况下应用。

图2　不同滚降系数下的S曲线

2预滤波原理

由式(1)可知，当Gardner算法应用在MQAM调制时，即使定时准确，由于QAM信号的幅值多样性，符号相同时，两符号中间值可能不过零，因此，Gardner时钟误差检测算法的自噪声十分严重。于是一些修正类算法和预处理类算法在文献[10]中被提出。本文采用了一种添加预滤波的改进Gardner算法，减小了自噪声增大带来的定时抖动，增加了系统的抗噪性能。

由于Gardner定时算法的误差估计特性，很容易得到逼近零抖动的条件[3]。假如基带信号具有以T为周期的过零点，也就是将信号滤波成为在t=kT+T/2,∀k，为零点的信号。

设接收的QAM信号基带复包络为：

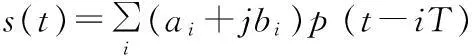
(8)

式中，

p(t)gT(t)⊗gR(t)⊗hp(t)。

(9)

gT(t)为升余弦成型函数；gR(t)为匹配滤波函数；hp(t)为预滤波函数；⊗为卷积符号。

由零抖动的条件[11]可知，

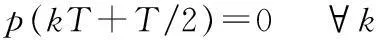
(10)

设p(t)傅里叶变换为P(f)，式(10)等价于式(11)：

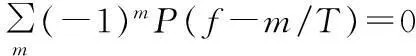
(11)

当P(f)为带宽小于1/T的带限信号，则上式等价于

P(f)=P(f-1/T)， 0≤f<1/T。

(12)

对于升余弦信号，则满足ZJ条件的一种预滤波器的频域表达式为：

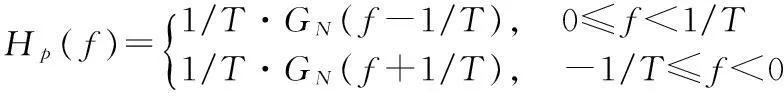
(13)

式中，GN(f)为升余弦信号的频域表达式。对于升余弦成型的信号来说，推导出预滤波的表达式为[3]：

hp(t)=gR(t)cos(πt/T)。

(14)

3性能仿真分析

本文方法适用于每符号采2个点的定时误差检测，在Gardner算法中预滤波模块加在插值后，算法框图如图3所示。

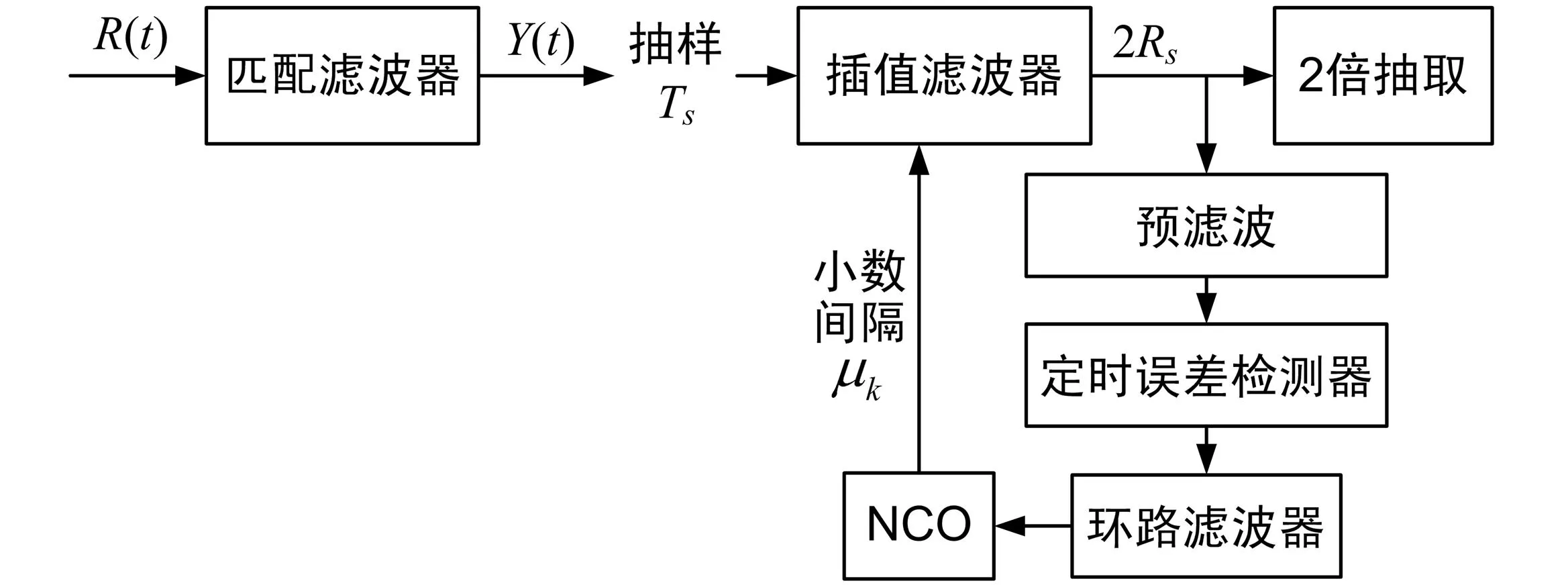
图3　加预滤波的Gardner算法原理

通过Matlab及Modelsim对预滤波前后的Gardner定时算法性能进行了仿真，采用64QAM调制解调，经过高斯信道，Eb/N0=18，成型系数为0.2，得到结果如图4、图5、图6和图7所示。

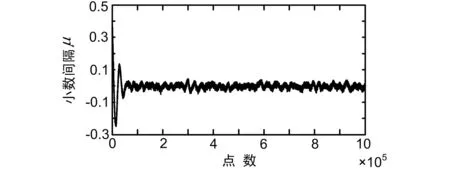
图4　加预滤波前小数间隔收敛曲线

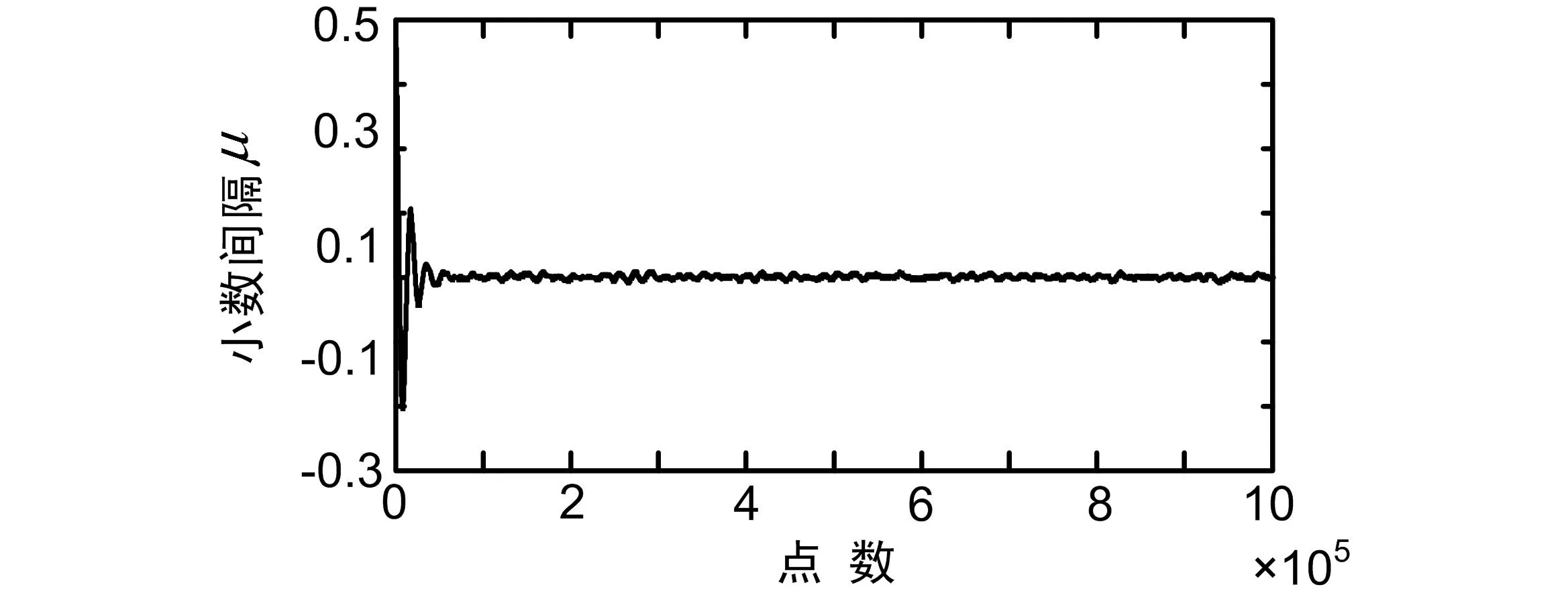
图5　加预滤波后小数间隔收敛曲线

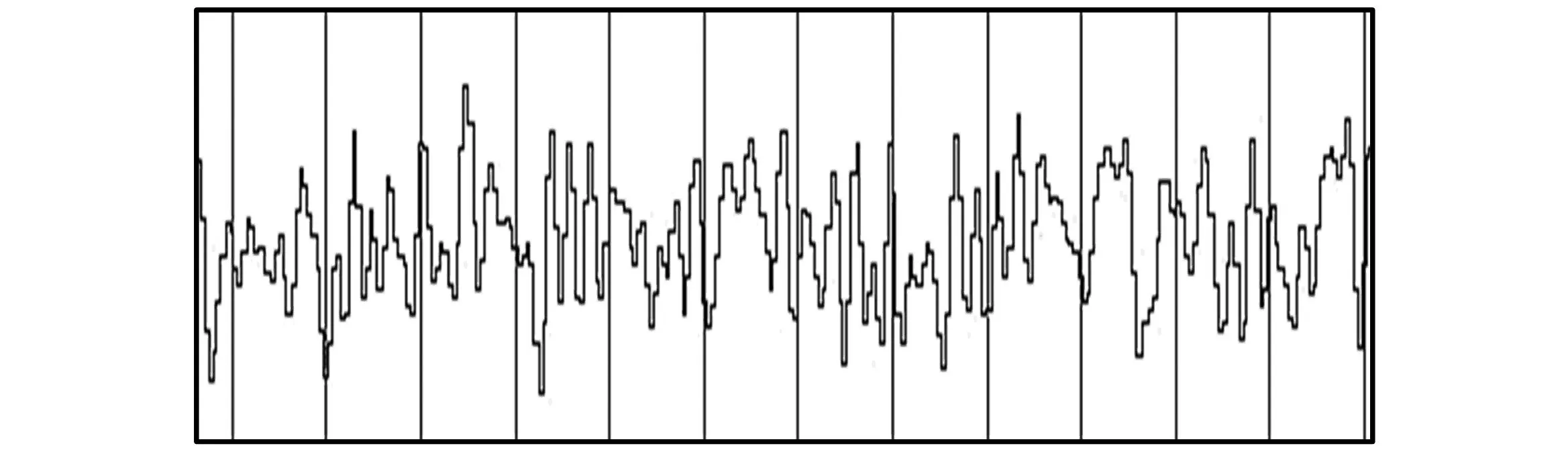
图6　加预滤波前2倍符号采样率的时域波形

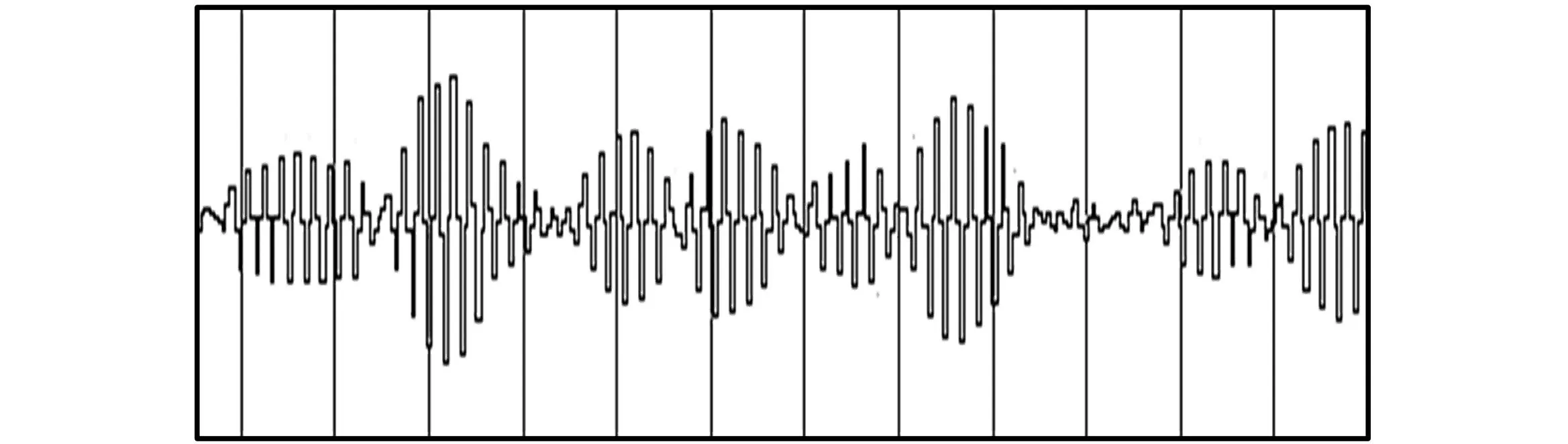
图7　加预滤波后2倍符号采样率的时域波形

从图7中可以看到，预滤波之后，采样点成为在t=kT+T/2处过零的符号，如果定时准确，使用原始Gardner定时误差检测算法，前后2个符号所得的误差为零，改善了QAM信号2个符号不具有过零点引起的自噪声，同时由于过预滤波之后的信号与成型系数无关，因此对成型系数较小时引起的较大自噪声也有所改善。

4结束语

通过对预滤波前后的Gardner定时算法性能进行了仿真，可以看到该定时算法能够使定时抖动明显减小，较好地抑制了在高阶调制(MQAM)和低滚降系数成型下定时算法的自噪声，提升了定时性能。

将该方法应用于吉比特高速调制解调时，由于FPGA处理速度的限制，需要并行解调[12]，定时模块也需并行实现。当FPGA处理串行数据时，数据只有一路，系统整体吞吐率就是该路的处理吞吐率。但如果采用并行数据处理方式，比如说8路数据，系统的整体吞吐率为单路的处理吞吐率8倍。所以，采用该定时同步算法并行处理方式方能满足高阶调制，低滚降系数成型下的高速信号处理的需求。

参考文献

[1]林长星.2Gbps高速通信解调技术及其实现研究[D].北京:清华大学,2012.

[2]李志勇,李文铎.155Mbps毫米波QAM解调器设计[J].电子学报,2010,38(6):1 419-1 424.

[3]SHI K,WANG Y,SERPEDIN E.On the Design of a Digital Blind Feedforward,Nearly Jitting-Free Timing Recovery Scheme for Linear Modulation[J].IEEE Transactions on Communications,2004,52(9):1 464-1 468.

[4]黄磊,许科,崔慧娟,等.适用于低滚降系数成型脉冲的定时恢复方案[J].电子技术应用,2011,37(8):117-119.

[5]GARDNERF M.Interpolation in Digital Modems- PartI:Fundamentals[J].IEEE Trans.Commun.,1993,41(3):501-507.

[6]LAYS E,GARDNER F M.Interpolation in Digital Modems-PartII:Implementation and Performance[J].IEEE Transactions on Broadcasting,1993,41(6):908-1 008.

[7]季仲梅,杨洪生,工大鸣,等.通信中的同步技术及应用[M].北京:清华大学出版社,2008.

[8]李建海,成亚勇.QPSK调制解调中的Gardner定时恢复算法研究与性能分析[J].无线电工程,2004,34(10):55-59.

[9]付永明,朱江,琚瑛珏.Gardner定时同步环路参数设计及性能分析[J].通信学报,2012,33(6):194-198.

[10]付永明，朱江，琚瑛珏，等.Gardner定时同步环路自噪声消减算法[J].现代电子技术.2011,34(21):92-95.

[11]NUNZIO A D,LUISE M.Design and Analysis of a Jitter-Free Clock Recovery Scheme for QAM Systems[J].IEEE Transactions on Communications,1993,41(9):1 296-1 299.

[12]宋广怡.超宽带高速数据传输技术研究[J].无线电工程,2014,44(5):23-25.

冯彐然女，(1989—)，硕士研究生。主要研究方向：通信与信息系统。

韩军男，(1964—)，研究员。主要研究方向：微波通信设备与系统。

引用格式：冯彐然，韩军.一种逼近零抖动的Gardner定时误差检测算法[J].无线电工程,2016,46(1):50-52，56.

A Gardner Timing-error Detection Algorithm with

Nearly Zero Jitting

FENG Xue-ran1,2,HAN Jun1

(1.The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China；

2.ScienceandTechnologyonInformationTransmissionandDisseminationinCommunication

NetworksLaboratory,ShijiazhuangHebei050081,China)

AbstractWith the increase of wireless communication rate and the decrease of frequency resources,the high order modulation and shaping with low rolloff factor should be used to improve the spectrum utilization of the whole system and achieve high-rate transmission.But the high order modulation and shaping with low rolloff factor may increase the self-noise and timing jitting,making the system out of synchronization.To solve the problem,a Gardner timing-error detection algorithm with zero jitting is studied for high order modulation(MQAM)and shaping with low rolloff factor.The algorithm is based on pre-filter.By simulation,the waveform in time domain before and after pre-filtering and the fraction interval jitting are obtained.In these figures,the change in the waveform before and after the pre-filtering is shown clearly and the timing jitter is decreased significantly.

Key wordsbit timing recovery;low rolloff factor;MQAM;pre-filter;zero jitting

作者简介

基金项目：国家部委基金资助项目。

收稿日期：2015-10-19

中图分类号TN911

文献标识码A

文章编号1003-3106(2016)01-0050-03

doi:10.3969/j.issn.1003-3106.2016.01.12