可调整多粒度覆盖粗糙集模型
2016-01-20叶培培吕跃进
叶培培,吕跃进
(广西大学数学与信息科学学院, 广西南宁530004)
可调整多粒度覆盖粗糙集模型
叶培培,吕跃进
(广西大学数学与信息科学学院, 广西南宁530004)
摘要:多粒度粗糙集是近几年粗糙集理论的一个研究热点,而其中的多粒度覆盖粗糙集的研究集中于模型的推广,文中分析乐观多粒度覆盖粗糙集下近似的不足之处,提出了一种可调整的多粒度覆盖粗糙集。研究可调整多粒度覆盖粗糙集的性质,并提出一种粒度重要性的启发式约简算法,实例分析结果验证该方法的可行性。
关键词:多粒度,覆盖信息系统,粒度约简
0引言
粗糙集理论[1-2]是波兰数学家Pawlak于1982年提出的,它可以作为一种分析和处理不确定、不精确、不完整信息的有效方法。经过三十多年的发展,已被广泛应用到数据挖掘[3]、知识发现[4]、图像处理[5]、模式识别[6]等领域。经典粗糙集通过构建不可分辨的二元关系(等价关系)定义上、下近似来刻画未知的概念。随着研究的进一步深入,等价关系逐步被弱化,如优势关系[7]、容差关系[8]、相似关系[9]等。
从粒的角度看,经典粗糙集及其推广的粗糙集模型都是在单粒度空间上进行目标概念刻画的。然而在粒计算理论中,多粒度是最重要的概念之一。多粒度表示在两个甚至多个不同的粒空间上对目标概念问题进行研究。同时由于实际问题处理的需要,文献[10]提出了多粒度粗糙集的概念。文献[11-12]将多粒度的思想引入到覆盖粗糙集中,其中文献[11]提出了一种基于覆盖近似空间中一个对象最小描述的多粒度覆盖粗糙集模型,经分析其模型中下近似的定义过于宽松,即在m个粒结构下只要一个粒结构中存在Cij∈MdCi(x),使得Cij⊆X成立,那么x就属于X的下近似。文献[12]根据单粒度的覆盖粗糙集(交运算成立)推广到多粒度覆盖粗糙集,其不足同文献[11]的一样。基于此,本文提出了可调整多粒度覆盖粗糙集,在m个粒结构下只要一定数目的粒结构中存在知识粒[x]Pi,满足[x]Pi⊆X,就可认为x属于X的下近似,并研究可调整多粒度覆盖粗糙集的性质。
另一方面,对粒度约简算法的研究,目前有文献[13]在等价关系下研究悲观多粒度粗糙集的一种粒度重要度,以此为启发设计了一种粒度约简算法。文献[14]在等价关系下研究悲观多粒度粗糙集的粒度约简,以粒度的信息量为启发因子,设计了一种信息量的悲观多粒度约简算法。学者研究的是在等价关系下的多粒度粗糙集粒度约简,对于非等价关系的尚无研究,本文研究一种非等价关系在可调整多粒度覆盖粗糙集下的一种粒度约简的算法。
1预备知识
1.1 单粒度粗糙集

定义2设(U,AT,V,F)为信息系统,∀A⊆AT,定义A上的不可分辨关系[2]:
IND(A)={(x,y)∈U2|,∀a∈A,f(x,a)=f(y,a)}。
不可分辨关系满足传递性、自反性和对称性,为U上的一个等价关系,由这个等价关系可以导出U上的一个划分,记为U/IND(A),∀x∈U,那么x的等价类可记为[x]A,[x]A={y∈U|(x,y)∈IND(A)}。
定义3设(U,AT,V,F)为一个信息系统,对∀X⊆U,A⊆AT,定义X关于属性A的下、上近似[2],分别记为:
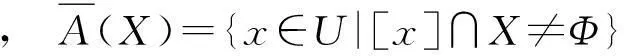
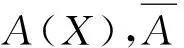
U/IND(A)={[x]A|x∈U},
也被称为一个粒结构。
1.2 覆盖粗糙集
定义4设U为论域,C={c1,c2,…,cn}是论域U上的一个覆盖。对∀x∈U,x在覆盖近似空间
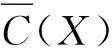
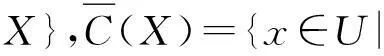
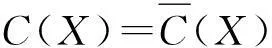
1.3 多粒度覆盖粗糙集
定义6设U为论域,C1,C2,…,Ck为论域上的一族覆盖。对∀X⊆U,则X的多粒度覆盖粗糙集定义[11]如下:
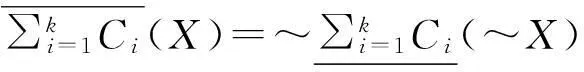
命题1设U为论域,C1,C2,…,Ck为论域上的一族覆盖[11],对∀X⊆U,则有:
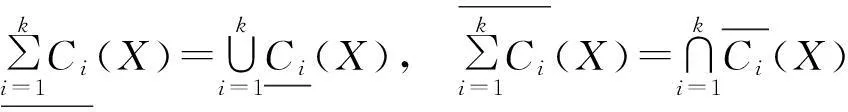
命题1说明了多粒度覆盖粗糙集的下近似是所有单粒度覆盖下近似的并,也就是说只要其中一个粒度存在Cij∈MdCi(x),使得Cij⊆X成立,那么x就属于X的下近似;而上近似就是所有单粒度覆盖上近似的交。
2可调整多粒度覆盖粗糙集模型
由定义6知,覆盖近似空间中一个对象最小描述的多粒度覆盖粗糙集(乐观多粒度覆盖粗糙集)的下近似仅要求在m个粒结构下只要有一个粒结构中存在Cij∈MdCi(x),使得Cij⊆X成立,x就属于X的下近似,这个条件太过于宽松。本文则在m个粒结构下只要有一定数目的粒结构中存在知识粒[x]Pi,使得[x]Pi⊆X,就认为x属于X的下近似。并且用参数α来控制满足条件的粒结构的个数,于是称此为可调整多粒度覆盖粗糙集。这样就能够解决对象最小描述诱导的多粒度覆盖粗糙集下近似过松的问题。
由于在覆盖决策信息系统中,每个属性都可以产生一个覆盖,即每个属性都可以产生一个粒度,所以本文研究的可调整多粒度覆盖粗糙集中的覆盖是属性产生的覆盖。
2.1 可调整多粒度粗糙集模型的定义
定义7设U是有限论域,C是U的一个子集族,如果C中的子集都是非空的,且∪C=U,则称C是U的一个覆盖。若C={C1,C2,…,Cm}中的每个Ci(i≤m)都是U的覆盖,则称C是U的覆盖族[16]。
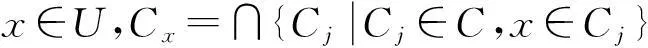
定义9Δ={Ci:i=1,2,…,m}是U的一族覆盖,∀x∈U,Δx=∩{Cix:Cix∈Cov(Ci),x∈Cix},则Cov(Δ)={Δx:x∈U}也是U的一个覆盖,称其为由Δ诱导的覆盖[18]。
定义10设(U,AT,V,F)为一信息系统,P1,P2,…,Pm⊆AT,对∀X⊆U,其特征函数可定义为:
其中[x]Pi是属性集Pi产生的覆盖中x所在的类。
定义11设U为论域,P1,P2,…,Pm⊆AT,对∀X⊆U,X关于属性集P1,P2,…,Pm的可调整的多粒度覆盖粗糙集下上近似可分别定义如下:
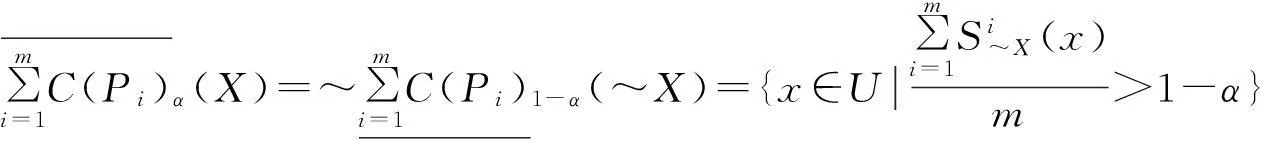
其中:α∈(0,1],C(Pi)是由属性集Pi诱导覆盖。
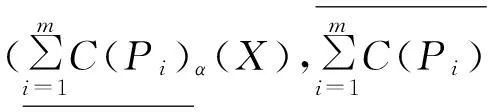
2.2 可调整多粒度覆盖粗糙集性质
定理1设S=(U,AT,V,F)为一信息系统,P1,P2,…,Pm⊆AT,∀X,Y⊆U,可调整的多粒度覆盖粗糙集有以下性质:
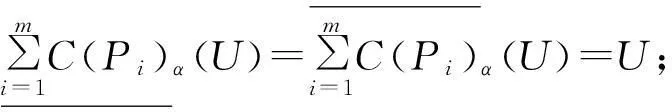
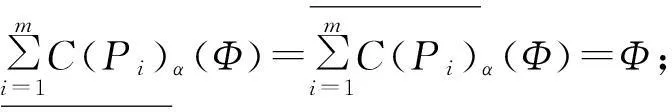
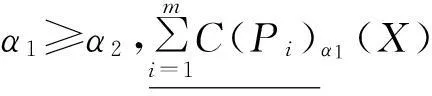
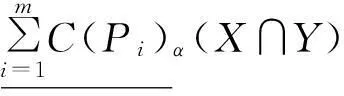
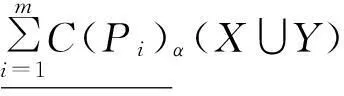
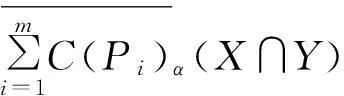
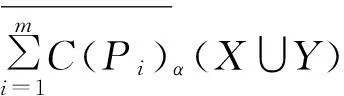
证明①和②根据定义2易证。
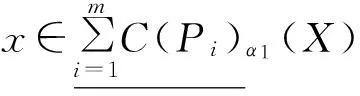
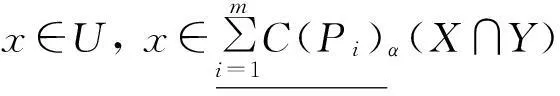

同理可证⑥⑦。
3粒度约简
定义12设(U,AT∪{d},V,F)是覆盖决策信息系统,P1,P2,…,Pm⊆AT,P={P1,P2,…,Pm}, 0≤α≤1,D=C{d}={D1,D2,…,Dn},分别定义:
为下上近似分布函数。若:
①如果Lp-{Pi}(D)=LP(D),则称Pi在粒度集P是不必要的;否则Pi在粒度集P是必要的。
②如果存在Q⊆P,使得LQ(D)=LP(D),则称Q是P的下近似协调集,若对Q的任意真子集Q′,都有LQ(D)≠LQ′(D),则称Q是P的下近似约简。
③如果存在Q⊆P,使得UQ(D)=UP(D),则称Q是P的上近似协调集,若对Q的任意真子集Q′,都有UQ(D)≠UQ′(D),则称Q是P的上近似约简。
如果Q既是P的上近似分布约简又是P下近似分布约简,那么称Q是P的近似分布约简。
为了找到约简,基于多粒度下近似粒度相对重要性的定义,很据粒度相对重要性找出信息系统的约简集,由此得出最小的约简。
定义13设(U,AT∪{d},V,F)是覆盖决策信息系统,其中a∈Pi⊆AT,D=C{d}={D1,D2,D3,…,Dn},则粒度Pt在P下重要性为:
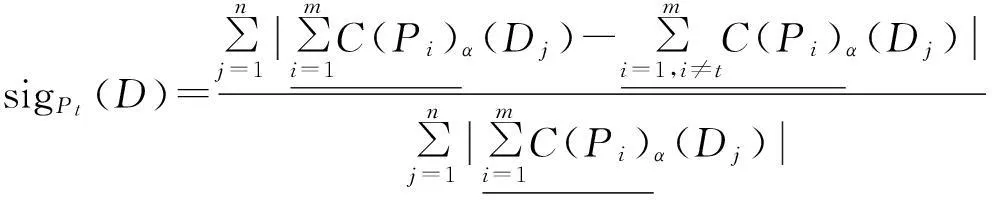
由定义可知sigPt(D)大于或等于零。当sigPt(D)=0时,表示约去粒度Pt后,决策类D的下近似分布不发生变化,则Pt是关于决策类D下近似不重要的。当sigPt(D)>0时,表示约去粒度Pt后决策类D的下近似分布发生变化,则Pt是关于决策类D下近似重要的。
约简算法:
输入:覆盖决策信息系统(U,AT∪{d},V,F),P1,P2,…,Pm⊆AT,Pi∩Pj=Φ(i≠j,i,j=1,2,…,m),其中P={P1,P2,…,Pm};
输出:该覆盖信息系统的约简;
Step 1: 对每一个Pi∈P,计算其产生的诱导覆盖C(Pi)以及C(D);
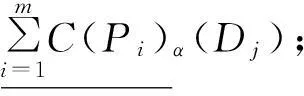
Step 3: 对每一个Pi∈P,计算sigPi(D), 令P的下近似约简为R,R=Φ;
Step 4: 判断LRα(D)=LPα(D)是否成立,若成立则转step 6,否则转step 5;
Step 5: 对任意的Pi∈P,取sigPi(D)为最大值时的Pi,使R=R∪{Pi}, (i=1,2,…,m),转step 4;
Step 6: 输出R,R就是粒度集P的约简集。
例1如表1给出小汽车的信息,AT={P,M,S,MS,FS,L},其中P,M,S,MS,FS,L分别表示Price,Mileage,Size,Max-Speed,Fuel Sumption,Life每个属性都可以产生一个覆盖,其中将条件属性集分成3个粒度,P1={P,M},P2={S,MS},P3={FS,L},根据前面的定义和定理,对表1进行多粒度的粒约简。
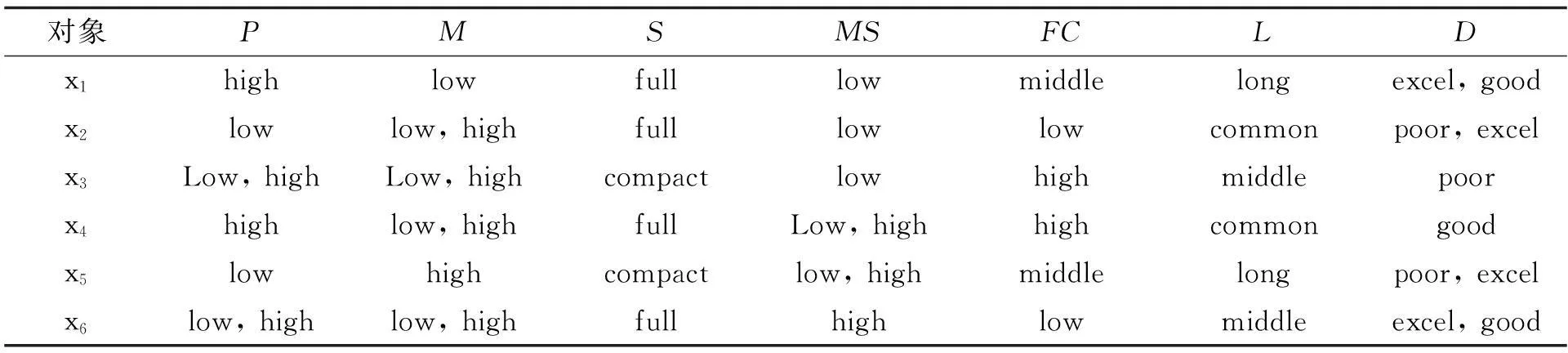
表1 覆盖决策信息系统
每个属性产生的覆盖如下:
C({FS})={{x1,x5},{x2,x6},{x3,x4}};
C({L})={{x1,x5},{x2,x4},{x3,x6}};
C({D})={{x1,x6},{x2,x5},{x2,x3,x5},{x1,x4,x6}}。
两个属性诱导的覆盖:
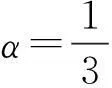

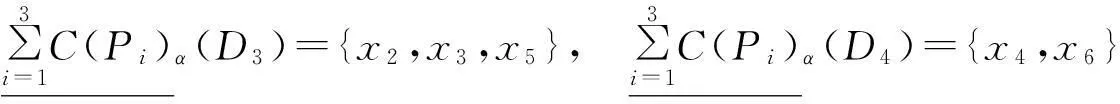
利用约简算法计算各粒度的重要性:
粒度P1的重要性:
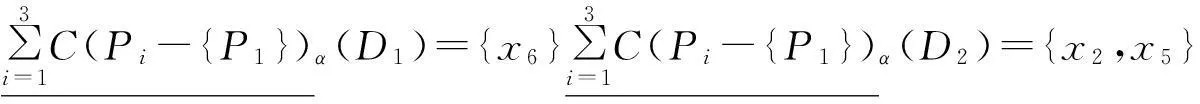
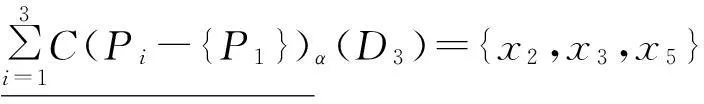
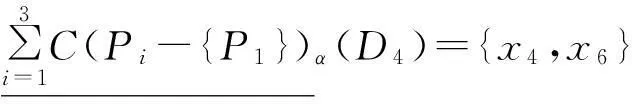
sigP1(D)=0。
粒度P2的重要性:
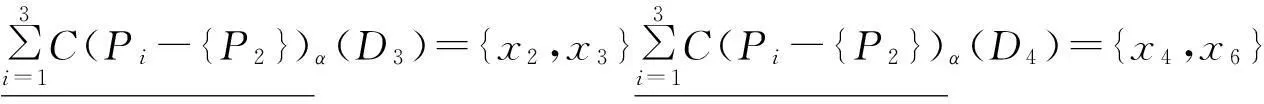

粒度P3的重要性:
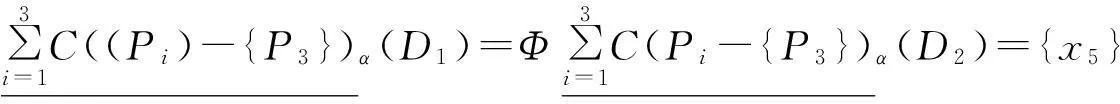
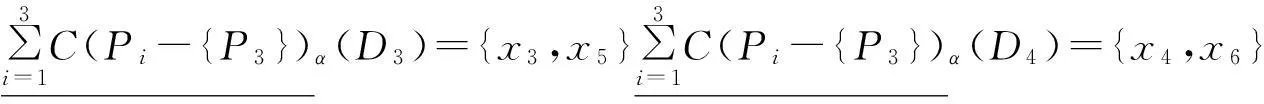
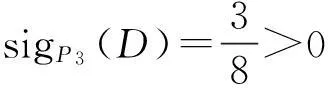

4结语
本文提出了可调整多粒度覆盖粗糙集模型,对多粒度覆盖粗糙集模型进行了推广。同时定义了粒度重要性,提出了粒度约简算法。用粒度相对于粒度集重要性找出重要的粒度,对粒度进行约简。通过实例对文中的算法进行了验证,结果表明粒度约简方法的有效性、合理性。
参考文献:
[1]PAWLAK Z.Rough Sets[J]. International Journal of Computerand Information sciences, 1982, 11(5): 341-356.
[2]PAWLAK Z.Rudiments of rough sets[J]. Information Sciences, 2007, 177(1): 3-27.
[3]ZHANG Jun-bo, LI Tian-rui, CHEN Hong-mei.Composite rough sets for dynamic data mining [J]. Information Sciences, 2014, 257:81-100.
[4]LI Y L, XIAO D M.Bifurcations of a predator-prey system of Holling and Leslie types[J]. Chaos, Solitons and Fractals,2007,34 (2):606-620.
[5]WANG Q, FAN M, WANG K.Dynamics of class of Nonautonomous semi-ratio-dependent predator-prey systems with functional responses[J]. Math Anal Appl, 2003, 278(2):443-471.
[6]LIANG Ji-ye, WANG Feng, DANG Chuang-yin, et al.An efficient rough feature selection algorithm with a multi-granulation view[J]. Information Journal of Approximate Reasoning, 2012, 53(6): 912-926.
[7]GRECO S, MATARAZZO B, SLOWINSKI R.Rough sets theory for multicriteria decision analysis[J]. European Journal of Operational Research, 2001, 129(1): 1-47.
[8]LEUNG Y, LI D.Maximal consistent block technique for rule acquisition in incomplete information systems[J]. Information Sciences, 2003, 153: 85-106.
[9]STEFANOWSKI J, TSOUKIAS A.Incomplete information tables and rough classification[J]. Computational Intelligence, 2001, 17(3): 545-566.
[10]QIAN YU-HUA, LIANG JI-YE.Rough set method based on multi-granulations[C]//5th IEEE International Conference on Cognitive Informatics. Beijing:IEEE,2006 :297-304.
[11]周国正.一种多粒度覆盖粗糙集模型[J]. 齐齐哈尔大学学报:2012, 28(5): 10-13.
[12]李气芳,李进金,林国平.多粒度覆盖信息系统的属性约简方法比较[J]. 计算机工程与应用,2013, 49(10):121-124.
[13]桑妍丽, 钱宇华.一种悲观多粒度粗糙集中的粒度约简算法[J]. 模式识别与人工智能,2012, 25(3):361-366.
[14]孟慧丽, 马媛媛, 徐久成.基于信息量的悲观多粒度粗糙集粒度约简[J]. 南京大学学报:自然科学版,2015, 51(2):343-348.
[15]张文修, 梁怡, 吴伟志.信息系统与知识发现[M]. 北京:科学出版社,2003.
[16]BONIKOWSKI Z, BRYNIARSKI E, WYBRANIEC U .Extensions and intentions in the rough set theory Information Science[J]. Information Sciences, 1998, 107:149-167.
[17]胡军,王国胤.覆盖粒度空间的层次模型[J]. 南京大学学报:自然科学版,2008, 44(5):551-558.
[18]CHEN De-gang,WANG Chang-zhong,HU Qing-hua.A new approach to attribute reduction of consistent and inconsistent covering decision systems with covering rough sets[J]. Information Sciences,2007, 177(17):3500-3518.
(责任编辑梁碧芬)
Adjustable multi-granulation covering rough set model
YE Pei-pei, LYU Yue-jin
(College of Mathematics and Information Science, Guangxi University, Nanning 530004,China)
Abstract:Multi-granulation is a research focus in rough sets in recent year, of which multi-granulation covering rough set research focused on the model of the extension.By analyzing the limitations of the optimistic multi-granulation covering rough set, the adjustable multi-granulation covering rough set is proposed.The properties of the adjustable multi-granulation covering rough sets are discussed.Furthermore,the heuristic algorithm of the granular significance is introduced.The experimental results show the effectiveness of the approach.
Key words:multi-granulation; covering information system; granular reduction
中图分类号:TP181
文献标识码:A
文章编号:1001-7445(2015)06-1603-08
doi:10.13624/j.cnki.issn.1001-7445.2015.1603
通讯作者:吕跃进(1958—),男,广东龙川人,广西大学教授; E-mail:lvyjin@126.com。
基金项目:国家自然科学基金资助项目(71361002);广西自然科学基金资助项目(2013GXNSFAA019016)
收稿日期:2015-09-21;
修订日期:2015-10-30
