基于气象相似度与马尔科夫链的光伏发电预测方法

海　涛，闻科伟，周　玲,2，胡　翔，张　朝

(1.广西大学电气工程学院， 广西南宁530004；2.广西电力职业技术学院动力工程系， 广西南宁530007)



基于气象相似度与马尔科夫链的光伏发电预测方法

海涛1，闻科伟1，周玲1,2，胡翔1，张朝1

(1.广西大学电气工程学院， 广西南宁530004；2.广西电力职业技术学院动力工程系， 广西南宁530007)

摘要：针对目前光伏发电预测中实用性较低、预测精度不高、气象条件利用不充分和预测跟踪性能较差等现象，设计出基于气象相似度与五状态马尔科夫链的光伏发电预测方法。该方法利用神经网络建立气象相似度—发电量相似度的过渡模型，用该模型预测可获得预测日发电量的预测结果，最后分别用三状态和五状态的马尔科夫链修正预测结果。实验结果表明：相比不充分利用气象条件的神经网络预测方法，基于气象相似度与五状态马尔科夫链的光伏发电预测方法具有较高的预测精度、实用性和良好的预测跟踪性能。

关键词：气象相似度；马尔科夫链；神经网络；光伏发电；预测方法

光伏发电在减少环境污染、缓解能源危机、改善能源结构等方面作用突出，已成为目前可再生能源重要发展方向[1]。但是光伏系统相比大电网是不可控的，其发电的随机性会对大电网造成冲击[2]。因此，需要加强光伏发电的预测研究，预先获得光伏发电系统的日发电量曲线，从而协调电力系统制定发电计划，减少光伏发电的随机化问题对电力系统的影响。

目前，光伏发电预测大多都采用神经网络的预测方法[3]，基本上都是从改进网络结构的角度去提高预测精度，而没有充分利用气象预报数据，这对于提高预测精度是有限的。而对于马尔科夫链，大多数模型都采用三状态的马尔科夫链，在修正的过程中，预测误差基本上都会落在中间区域[3]。因此，本文提出基于气象相似度和五状态马尔科夫链的光伏发电预测方法，旨在较大程度地提高光伏发电的预测精度、实用性和预测跟踪性能。

1光伏发电预测方法的确定

1.1　常用的几种光伏发电预测方法

目前主要光伏发电的预测方法主要有三类：一是建立光电转换效率模型，并结合太阳辐照度预报的预测法[4]；二是通过数理统计或数理统计和光伏组件仿真模型相结合的方法进行光伏发电预测，如利用光伏电站长期积累下来的发电数据和环境数据建立多元线性回归预测模型和灰色理论预测模型[5]；三是围绕神经网络、太阳辐照度和预测结果修正来展开[6]。太阳辐照度是影响光伏组件功率输出最主要的因素，是预测光伏发电量的关键因素。

1.2　基于气象相似度和马尔科夫链修正的预测模型

光伏发电具有较大的随机性和间歇性，极易受环境变化的影响，会造成基于光电转换效率模型和数理统计模型的预测方法出现较大的误差。理论上，建立基于神经网络和太阳辐照度的预测模型能获得高精度预测结果，但由于目前无法或很难获取预测日太阳辐照度，大多数预测模型都是不考虑太阳辐照度因素的神经网络预测模型[7]，其特点是将季节和天气类型量化，并用来表示太阳辐照度对光伏发电的作用，这样无法从实质上提高预测精度。为此，可以从两个角度解决以上问题：一是定义气象相似度，即认为前后两天同一时段的气象情况相似程度越高，则前后两天该时段的发电量越接近。由于现在逐时气象预报技术准确率很高，保证了发电量的预测精度和逐时跟踪性能；二是由于光伏发电波动性较大，马尔科夫链适合描述这类问题，故使用多状态的马尔科夫链修正能提高发电量的预测精度[8]。

2建立预测模型

本文从充分利用气象条件、定义气象相似度与发电量相似度过渡函数和利用五状态马尔科夫链修正预测结果三个角度建立光伏发电预测模型。

2.1　气象条件的充分选取和利用

太阳辐照度是提高光伏发电预测精度的关键点，但是无法或很难直接获取，所以必须充分挖掘与太阳辐照度相关性最强的气象参数。紫外线是太阳辐射的一部分，通常太阳辐射强时紫外线也强，不同季节、不同天气类型紫外线指数也不同。紫外线指数序列和天气类型序列能反映不同季节、不同天气类型的太阳辐照度。

理论太阳辐照度E是指太阳辐射不经任何遮挡和反射后到达地球表面的理论强度，它反映地球公转和自传的信息，即带有季节、日期、时段信息。精确计算预测日理论太阳辐照度序列是保证光伏发电预测精度的前提，其表达式为

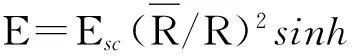
(1)

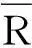
此外，使用紫外线指数序列、天气类型序列和理论太阳辐照度序列的组合气象参数可以间接替代太阳辐照度的作用。其中，气温也是影响光伏发电的因素，也必须考虑。

由于影响光伏发电功率的气象因素很多，各因素对发电功率的作用机理和影响程度各不相同，若不经处理直接将各气象因素作为模型输入，虽然全面考虑了各气象因素的影响，但会使输入空间的维数过高，模型结构趋于复杂，不利于模型的学习训练，从而降低模型的泛化能力。基于此前提，本文依据文献[9]中提出的考虑各种因素影响的新算法，识别并选取紫外线指数序列、天气类型序列、理论太阳辐照度序列和气温序列4个气象数据作为气象主导因素，从而在参考量选取上保证了预测精度。

2.2　气象相似度与发电量相似度过渡函数

假设理论太阳辐照度序列为E=[e0,…,e8]，紫外线指数序列为U=[u0,…,u8]，天气类型序列为W=[w0,…,w8]，气温序列为T=[t0,…,t8]。将前后两天同一段的紫外线指数比值、天气类型序列比值、理论太阳辐照度比值和气温比值作为自变量，将前后两天的该时段的发电量比值作为因变量，建立气象相似度与发电量相似度过渡函数[10]。由于光伏发电具有非线性的特性，所以该函数也是非线性的。由于实际情况的限制，本文只考虑8点到16点的发电情况，可表示为

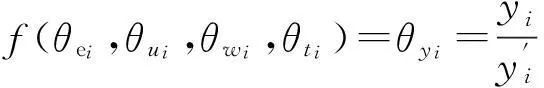
(2)

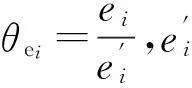
由于式(2)是非线性函数，用数学表达式求解会很困难。光伏电站运行一段时间，积累足够的历史数据后，对于该函数输入和输出都是确定的值，将其看做可用人工神经网络表示的黑箱[11]。本文有意弱化了神经网络的作用，强调了气象相似度对于提高预测精度的作用，故选用较为直观的RBF神经网络表示该非线性函数[12]，如图1所示。

图1气象相似度与发电量相似度过渡函数

Fig.1Transition function of meteorological and generating capacity similarity

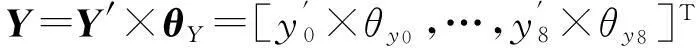
(3)

一般直接使用神经网络模型预测发电量的方式如图2所示。

图2RBF神经网络预测模型

Fig.2Forecast model of RBF neural network

相对于图2所示的网络，图1所示的网络的输入、输出数据数值等级接近，可获得更小的网络误差，但是在网络训练前，必须对训练样本作比值化处理[13]。选用用高斯函数作为RBF神经网络的径向基函数，即

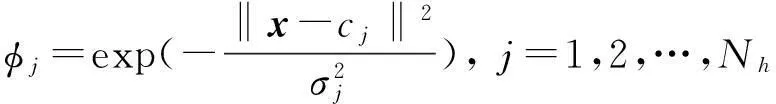
(4)

式中，φj是第j个隐层节点的输出；x=[x1,x2,…,xn]T是输入样本；cj是高斯函数的中心；σj是高斯函数的宽度；Nh是隐层节点数。RBF网络的输出为隐层节点的线性组合，如式(5)所示：

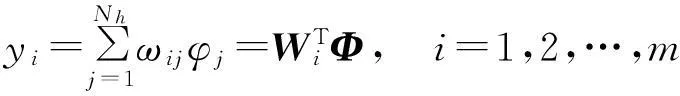
(5)

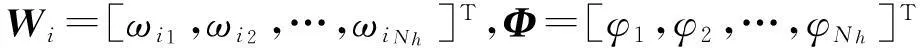
2.3　五状态马尔科夫链

用马尔科夫链可以修正式(3)的预测序列Y，可进一步提高发电量的预测精度。考虑到三状态马尔科夫链在状态转移过程中基本都会落在中间区域，修正精度不高，故本文使用五状态马尔科夫链。其基本思想：马尔科夫链能根据某参数当前的状态和发展趋势，预测该参数未来的状态，而且未来的状态只与当前的状态有关。式(6)表达的内容是随机过程当前时刻的状态只取决于前一个时刻的状态，满足式(6)的随机过程，即为马尔科夫链[14]。

P{Xn+1=En+1|Xn=En,…,X0=E0}=P{Xn+1=En+1|Xn=En}，

(6)

式(6)中,Xn为随机过程，n=0，1，2，…；En为随机过程所处的状态。

五状态马尔科夫链的态转移矩阵是一个5阶方阵，假设一步状态转移的5阶方阵为P(1)，假设初始状态向量为X0，后一步的状态向量为X1，第k步后的状态向量为Xk，则有

P(k)=(P(1))k,

(7)

X1=X0P(1),

(8)

Xk=X0P(k),

(9)

将连续若干天同一时刻的预测相对误差序列Er划分为5个区间，用来表示马尔科夫链的5个状态，通常用Ei表示5个状态,分别为E1、E2、E3、E4和E5。先使用黄金分割率将序列Er按式(10)划分为3个区域，此时获得马尔科夫链三状态，再将中间区间EMid等分为3份，便获得马尔科夫链五状态。

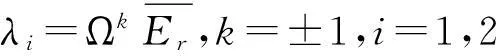
(10)

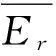
①将Er=[er1,…,ern]序列按上述的方法划分为五个区间E1~E5。

②将Er中的元素统计到E1~E5中，得到一步状态转移表，并提取出状态转移矩阵P(1)。

③选定初始状态向量X0=(x01,x02,x03,x04,x05)，以预测日前一天数据作初始状态向量。

④计算预测日的状态向量，记为X1=(x11,x12,x13,x14,x15)，X1=X0P(1)。

⑤预测ern+1，x11~x15分别对应ern+1处在E1~E5的概率。如果x13最大,则ern+1最有可能在E3。

⑦再以同样的方法修正其他时刻的发电量预测值。

3网络训练

由于将比值化的数据作为网络的输入，样本数据不能出现0，因此将可能是0值的样本数据做平移处理，如紫外线指数预报的数据会有0出现，可将所有的紫外线指数加1。所在区域也不会出现0 ℃以下的气温，指定天气类型为：晴天1、少云2、多云3、小雨4、中雨5、大雨6。网络训练的样本来自于所搭建的小型光伏电站的历史数据库，实验平台如图3所示。

图3　小型光伏电站实验平台

令网络输入为X=[θE,θU,θW,θT]，网络输出O=θY，如果有M组样本，则XM是输入向量组，OM是输出向量组。在进行训练之前，须将XM和OM进行归一化处理，以减小网络误差。由于篇幅有限，本文在此省略归一化处理的具体步骤，将归一化后的样本放入到X01=mapminmax(XM,0,1)，O01=mapminmax(OM,0,1)，以上步骤可消除输入数值上的差异对模型学习训练的影响。利用神经网络工具函数net=newrb(XM,OM,0.001)建立RBF神经网络，0.001是设定的网络误差，net是最终训练好的网络。本文根据经验参照下式进行设计[15]：

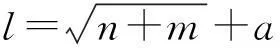
(11)

式中，l为隐含层节点数，n为输入层节点数，m为输出层节点数，α为0~10的调节常数。此外增加验证环节，隐含层节点数从0逐步增加，当隐含层节点数达到8个，网络的目标误差趋近于零，此时达到最优，故选择最终8个隐层节点作为神经网络的隐含层节点数。此时网络输出为最优逼近函数，网络的训练效果如图4所示，能获得更小的网络误差。

4发电量预测分析

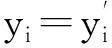
表1　预测所需的数据

将X=[θE,θU,θW,θT]归一化后输入所建立的RBF神经网络，即θY01=sim(net,X)，将θY01反归一化后获得前后两天发电量比值序列，即θY=[0.3810.4620.9250.4890.3020.9110.5300.5300.513]。2014年8月15日预测的发电量序列Y通过式(3)求得，即Y=[10.618.449.733.720.454.331.230.115.2]，真实值序列为[8.420.342.735.924.255.530.131.111.5]。基于气象相似度和非气象相似度的预测结果如图5所示，基于气象相似度预测曲线基本与真实的发电曲线吻合，前者均方根误差RMSE=3.23，精度(平均绝对百分比误差MAPE)为11.2%，预测跟踪性能良好；后者RMSE=7.48，精度为25.9%，预测跟踪性能较差。

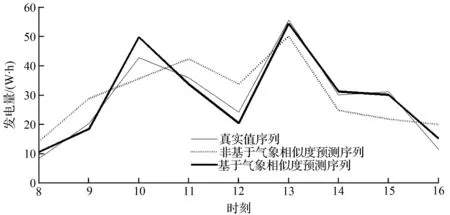
图5　基于气象相似度和非气象相似度的预测结果对比图

以2014年7月11日~2014年8月14连续35 d 13时基于气象相似度的预测结果为例，预测结果如表2所示，序号是按时间日期排序，将该表用于划分状态区间，并确认Er序列所属的状态。

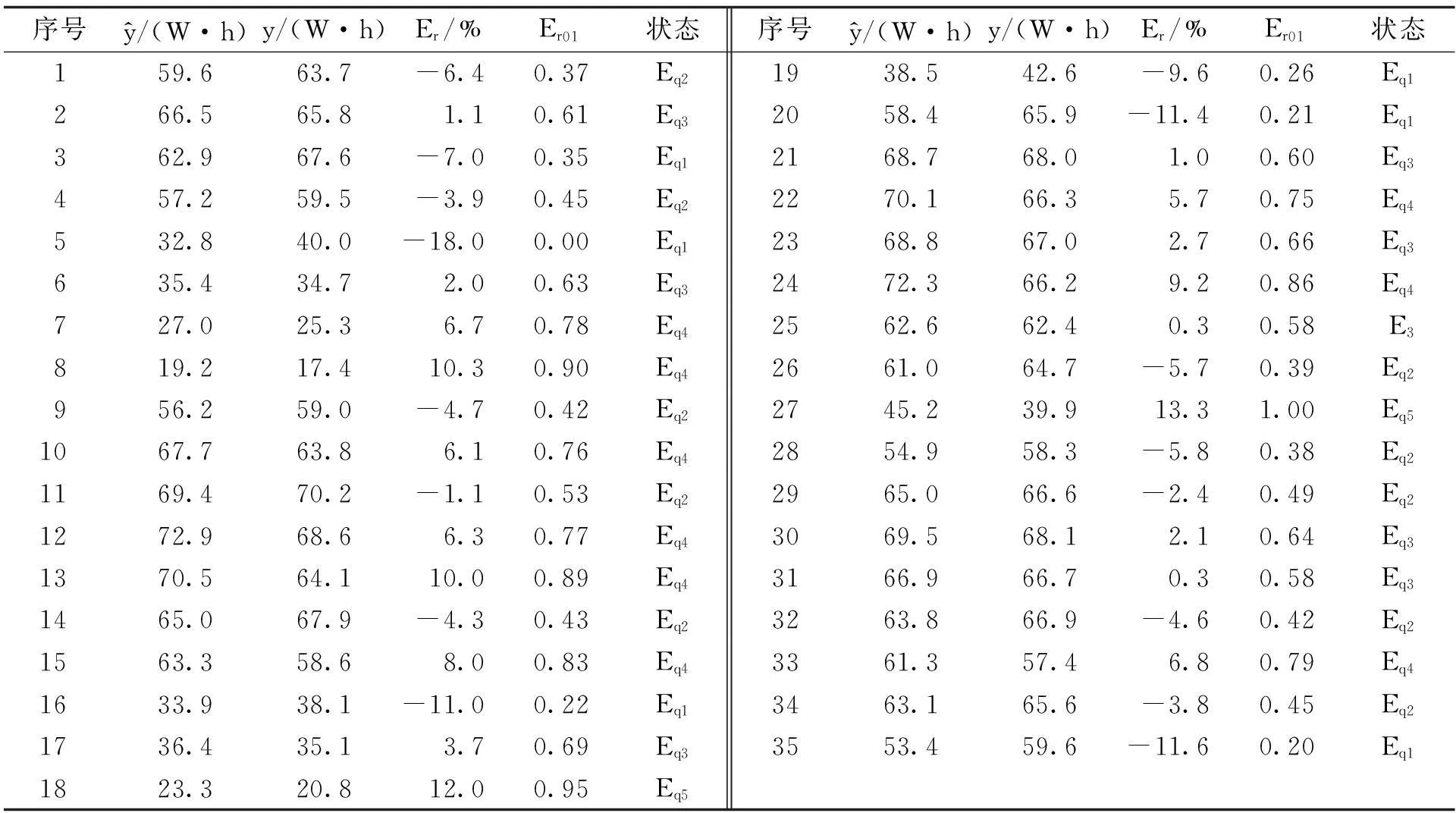
表2　基于气象相似度的预测相对误差

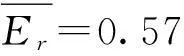
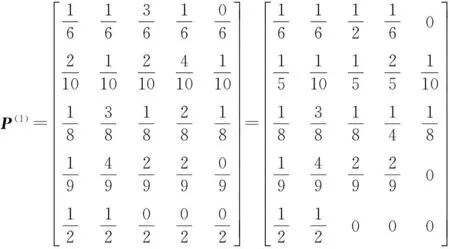
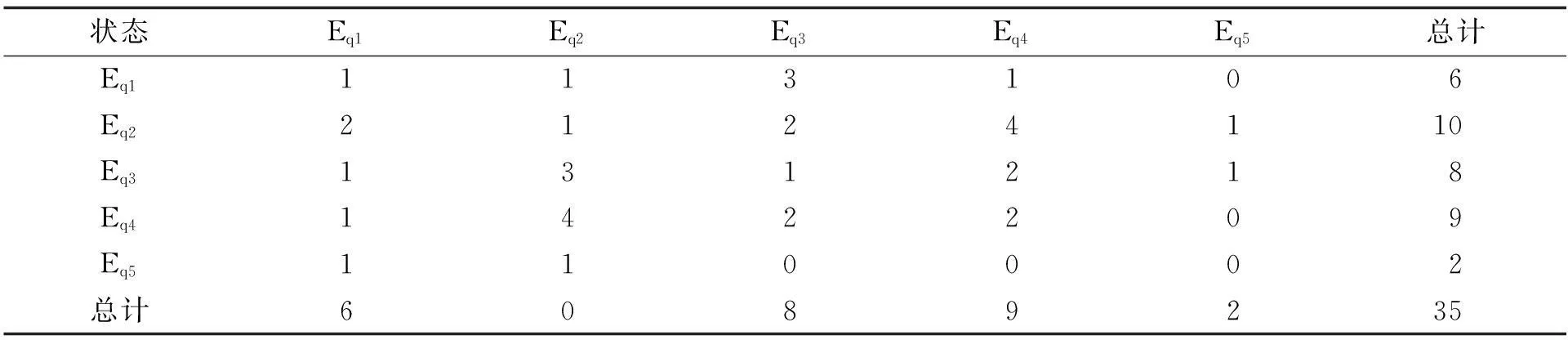
表3　状态转移表

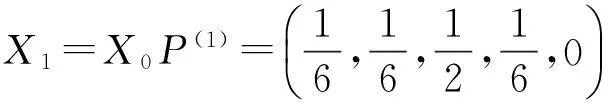
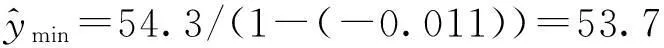
(12)

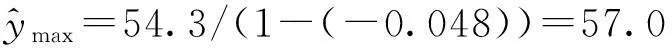
(13)

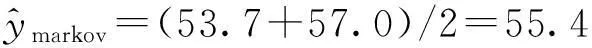
(14)

已知该日13时的真实发电量为y=55.5 W·h，未进行马尔科夫链的修正前的相对误差Er=(54.3-55.5)/55.5=-2.2%，进行马尔科夫链的修正后的相对误差Ermarkov=(54.5-55.5)/55.5=-0.18%。以同样的方式计算该日其他时刻的马尔科夫链的修正值，则2014年8月15日预测的发电量序列修正为：[10.121.846.233.321.155.432.530.214.3]，RMSE=2.31，精度为8%。用三状态马尔科夫链修正的结果为：[10.422.648.138.027.756.929.033.914.8]，RMSE=2.93，精度为10.1%。用三状态和五状态马尔科夫链修正前后的对比结果分别如图6所示，预测结果经马尔科夫链修正后，预测精度提高，且五状态链比三状态链的修正精度高。

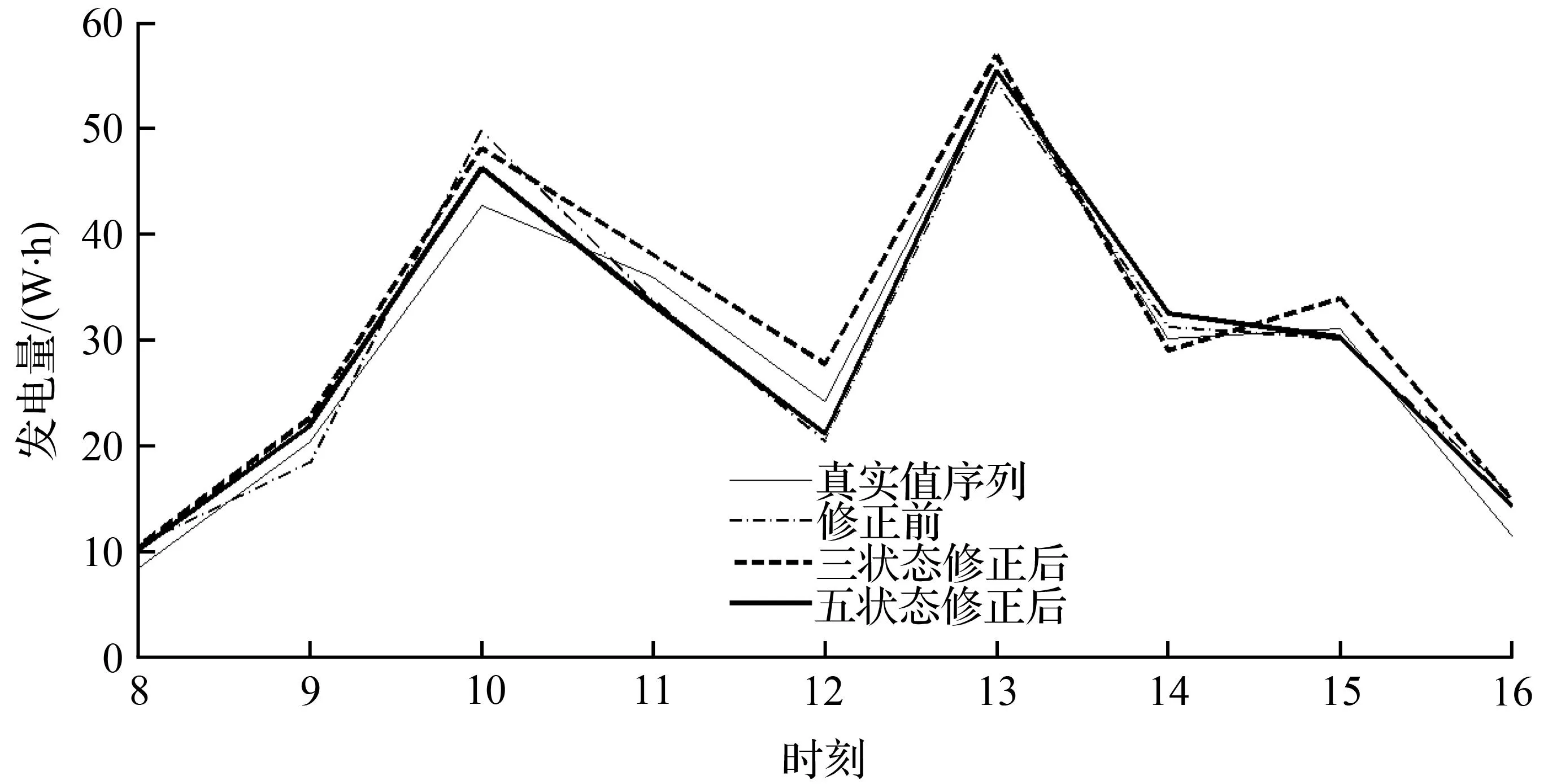
图6　经马尔科夫链修正预测结果的前后对比图

5结语

本文充分利用气象部门提供的预报数据和小型光伏电站的历史数据来预测光伏发电量，建立了气象相似度与发电量相似度的过渡函数，分别通过分析三状态马尔科夫链和五状态马尔科夫链对预测结果进行修正。同时直接将气象数据作为神经网络输入的方法，设计出基于气象相似度和马尔科夫链的光伏发电预测方法。

通过仿真模拟，其结果具有较高的预测精度、实用性和良好的预测跟踪性能，更能反映气象数据与发电量之间的关系。

参考文献：

[1]海涛，何江 .太阳能建筑一体化技术应用(光伏部分)[M]. 北京：科学出版社，2015.

[2]陈昌松，段善旭，殷进军 .基于神经网络的光伏阵列发电预测模型的设计 [J]. 电工技术学报，2009，24(9)：153- 158.

[3]景亚平，张鑫，罗艳 .基于灰色神经网络与马尔科夫链的城市需水量组合预测 [J]. 西北农林科技大学学报，2011，39(7)：229-234.

[4]蒋亚娟.光伏电池建模及其在光伏发电预测中的应用[D]. 武汉：华中科技大学电气与电子工程学院，2011.

[5]MELLIT A，ARAN A H，KHORISSI N，et al .An ANFIS-based forecasting for Solar radiation data from sunshine duration and ambient temperature[C]//IEEE Power Engineering Society General Meeting. Tampa, FL, USA: IEEE, 2007：1-6.

[6]李徐辉.光伏发电系统监控与发电预测[D]. 上海：东华大学机械工程学院，2012.

[7]张艳霞，赵杰.基于反馈型神经网络的光伏系统发电功率预测[J]. 电力系统保护与控制，2011，39(15)：96-101.

[8]刘赞科，汤旻安，郑悦.基于Markov模糊控制模型的交叉口设计与仿真研究 [J]. 广西大学学报：自然科学版，2015,40(3)：727-735.

[9]黎灿兵，李晓辉，赵瑞，等.电力短期负荷预测相似日选取算法[J]. 电力系统自动化，2008，32(9)：69-71.

[10]KITTIPONG M，LEE W J ，SOTHAYA R，et al.Multistage articial neural network short-term load forecasting engine with front-end weather forecast[J]. IEEE Transactions On Industry Applications,2007, 43(6):1410-1416.

[11]丁红，杨杰.小波变换集遗传算法神经网络的径流预测建模[J]. 广西大学学报：自然科学版，2012,37(3)：581-587.

[12]CHEN T Y，ATHIENITIS A K.Ambient temperature and solar radiation prediction for predictive control of HVAC systems and a methodology for optimal building heating dynamic operation[J]. ASHRAE Transaction，1996，102(1)：26-36.

[13]康洪波，刘瑞梅，侯秀梅.基于神经网络光伏发电预测模型的研究[J]. 电源技术，2013，37(3)：447-449.

[14]王义民，于兴杰，畅建霞，等.基于 BP 神经网络马尔科夫模型的径流量预测[J]. 武汉大学学报:工学版，2008，41(5)：14-17.

[15]李鹏梅，臧传治，王侃侃.基于相似日和神经网络的光伏发电预测[J]. 可再生能源，2013，31(10)：1-9.

(责任编辑裴润梅)

Design of photovoltaic power generation forecast system based on meteorological similarity and Markov chain

HAI Tao1，WEN Ke-wei1，ZHOU Ling1,2，HU Xiang1，ZHANG Zhao1

(1.College of Electrical Engineering，Guangxi University，Nanning 530004，China；

2.Guangxi Electrical Polytechnic Institute, Department of Powev Engineering， Nanning 530007，China)

Abstract:Due to low forecast accuracy, low practicability and inadequate using of meteorological conditions and poor forecast tracking performance in photovoltaic power generation forecasting, a new forecast method based on meteorological similarity and five state Markov chain is proposed. A neural network is used to establish meteorological and transition of electricity similarity model. And the result of forecast of power generation of one day is obtained by using the model. Early forecast results are revised respectively by using three and five state Markov chain. The practical experimental result shows that, compared with the method not making full use of meteorological condition of neural network, the method based on meteorological similarity and five state Markov chain has higher forecast accuracy, better tracking performance and practicability.

Key words:meteorological similarity; Markov chain; neural network; photovoltaic power generation; forecast method

中图分类号：TP274

文献标识码：A

文章编号：1001-7445(2015)06-1452-09

doi:10.13624/j.cnki.issn.1001-7445.2015.1452

通讯作者：海涛(1963—)，男(回族)，广西桂林人，广西大学教授级高级工程师；E-mail：haitao5913@163.com。

基金项目：国家自然科学基金资助项目(51267001)

收稿日期：2015-08-06；

修订日期：2015-09-05