一类单边Lipschitz系统的脉冲观测器设计

黄敢基，罗世贤，韦琳娜，陈武华

(广西大学数学与信息科学学院， 广西南宁530004)



一类单边Lipschitz系统的脉冲观测器设计

黄敢基，罗世贤，韦琳娜，陈武华

(广西大学数学与信息科学学院， 广西南宁530004)

摘要：为了研究一类单边Lipschitz非线性系统的脉冲观测器设计方法，构造了与脉冲发生时间序列相关的时变Laypunov函数分析相应观测误差系统的稳定性，结合线性矩阵不等式技术和单边Lipschitz条件，得到了的观测器指数收敛的充分条件和观测器增益矩阵的求解方法。研究结果表明：时变Laypunov函数能有效处理脉冲发生对误差系统稳定性的影响，而基于单边Lipschitz 条件设计的观测器比基于传统的Lipschitz 条件设计的观测器具有更广的应用范围。

关键词：单边Lipschitz系统；时变Lyapunov函数；脉冲观测器；指数稳定性

状态反馈控制在系统的各种综合问题中具有重要的作用，而观测器设计正是研究系统状态估计从而实现状态反馈的一个重要的研究课题。1973年，Thau[1]对一类Lipschitz非线性系统设计了状态观测器，由此提出了非线性系统的状态观测器设计问题。此后，众多学者对非线性系统观测器的设计方法进行了研究，主要采用的方法有类Lyapunov法[1]、坐标变换法[2]、扩展的Luenberger观测器设计方法[3]和扩展的Kalman滤波器方法[4]。近几年来，非线性系统的观测器理论研究的深度和广度得到了进一步的发展和完善,研究的对象涵盖了不确定系统、时滞系统、模糊系统及切换系统等[5-8]。在众多的非线性系统中，Lipschitz非线性系统的观测器设计问题一直是控制理论界的研究热点，如文献[9]研究了一类Lipschitz非线性系统的H∞观测器设计问题；文献[10]对具有不确定性的Lipschitz混沌系统设计了鲁棒区间观测器；文献[11]研究了Lipschitz非线性和系统输出相关系统的滑模观测器设计方法。文献[12]则讨论了一类Lipschitz非线性系统的自适应观测器设计问题，分别建立了系统含有和不含有未知参数时相应观测误差系统的稳定性判据。

一方面，在前述的非线性系统观测器研究成果中，都是假设系统输出可以连续测量的，但许多实际系统的输出仅在某些离散时刻可以量测，这使得采用连续时间更新的传统观测器设计方法不再适用。2007年, Raff等[13]提出了只需在离散时间更新状态的脉冲观测器。由于脉冲观测器相比于传统的观测器不仅能更有效地利用带宽，而且还能利用其离散信号的特点增加通信系统的保密性。因此，脉冲观测器一经提出便得到了一些学者的关注，如文献[14]研究了一类非线性系统的自适应脉冲观测器设计问题；文献[15]采用时变Lyapunov函数方法对一类具有状态时滞的Lipschitz非线性系统设计了脉冲观测器。而文献[16]则基于脉冲观测器给出了一类不确定线性系统的镇定方法。虽然脉冲观测器取得了一些研究成果，但相关的理论和方法还有许多值得进一步深入研究和完善的地方。另一方面，基于传统Lipschitz条件的观测器设计方法一般只适用于较小的Lipschitz常数[17]，近年来出现了一些基于单边Lipschitz条件[18]设计观测器的方法，所得结果相比由一般Lipschitz条件得到的结果具有更广的适用范围[19-20]。目前，对单边Lipschitz系统设计观测器的研究文献还相对较少，而关于单边Lipschitz系统脉冲观测器的研究则更少有报道。

基于上述讨论，本文拟对一类满足单边Lipschitz条件的系统设计脉冲观测器。根据脉冲观测器具有连续和离散模态混合的特点，采用分段连续的时变Laypunov函数分析相应观测误差系统的稳定性，利用凸组合技术和系统的单边Lipschitz条件，得到了观测误差系统指数稳定的线性矩阵不等式条件和脉冲观测器设计方法。进而给出两个实例的分析和仿真说明了本文方法的可行性和优越性。

1问题描述

在本文中，假设矩阵都具有适当的维数，矩阵M>(≥,<,≤)0分别表示M是一个实对称的正定(半正定，负定，半负定)矩阵。M的最大和最小特征值分别用λmax(M)和λmin(M)表示。单位矩阵用符号I表示。‖·‖表示向量的欧氏范数。N为正整数集，N0=N∪{0}。

考虑如下的非线性系统：

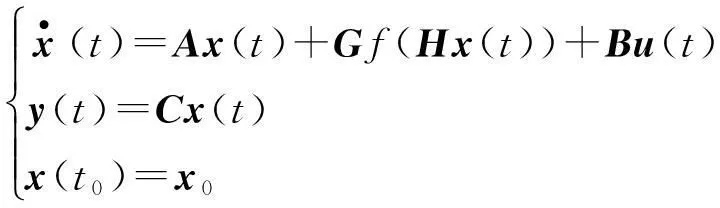
(1)

其中x(t)∈Rn是系统状态；u(t)∈Rm为可控输入；y(t)∈Rp为可测量的输出； A,B,C,G,H为常值矩阵。假设矩阵对(A,B)为能控，(A,C)为能观测的。非线性函数f(Hx(t))满足以下条件。

①存在ρ∈R，使得对任意的x1,x2∈Rn，成立:

〈f(Hx1)-f(Hx2),H(x1-x2)〉≤ρ‖H(x1-x2)‖2。

(2)

②存在σ,φ∈R，使得对任意的x1,x2∈Rn，成立:

(f(Hx1)-f(Hx2))T(f(Hx1)-f(Hx2))≤σ‖H(x1-x2)‖2+

φ〈H(x1-x2),f(Hx1)-f(Hx2)〉。

(3)

注1：条件①称为单边Lipschitz条件，其中ρ称为单边利普希茨常数；条件②称为二次型内部有界条件。任何满足Lipschitz条件的函数也必定满足单边Lipschitz条件和二次型内部有界条件，但反之未必成立。

对系统(1)设计脉冲观测器如下:

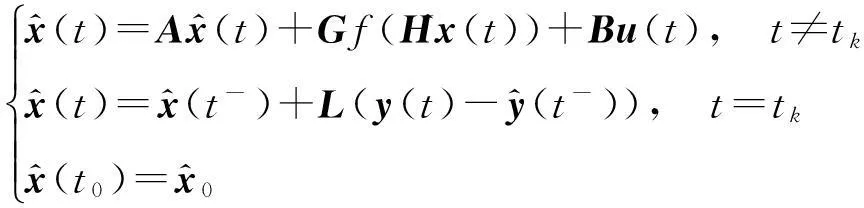
(4)

S(τ1,τ2)≜{{tk};τ1≤tk-tk-1≤τ2,k∈N0},

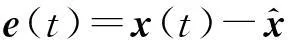
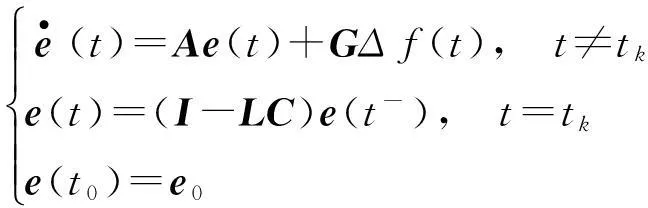
(5)

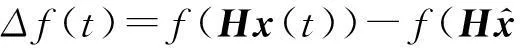
下面先给出在S(τ1,τ2)上系统(5)稳定的定义。

定义1对给定的初始时刻t0和脉冲序列S(τ1,τ2)，若存在M>0，γ>0，使得:

‖e(t)‖≤M‖e(t0)‖e-γ(t-t0),∀t≥t0,

对任意满足条件①、②的函数f(Hx(t))成立，则称系统(5) 在S(τ1,τ2)上全局指数稳定。

2主要结果

针对误差系统(5)具有连续和离散混合的动态特征，本文将构造与脉冲序列相关的时变Lyapunov函数分析系统(5)的稳定性。为此，先定义如下的两个时变函数ρ1(t),ρ0(t):[t0,+∞)→R+：

(6)

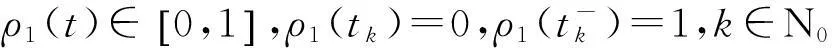
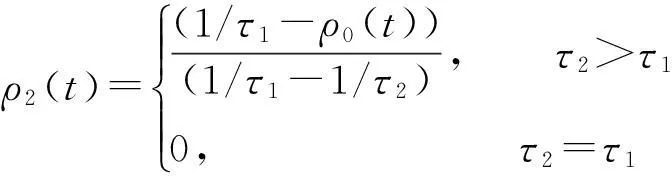
(7)

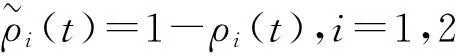
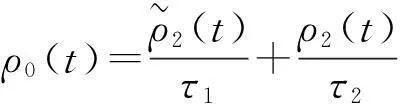
(8)

进一步，定义一个分段连续的时变的Laypunov函数如下：

V(t,e(t))=μρ1(t)eT(t)P(t)e(t)，t∈[tk,tk+1)，

(9)

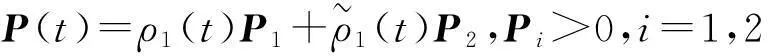
定理1考虑具有脉冲序列集{tk}∈S(τ1,τ2)的观测误差系统(5)。给定正标量r，μ∈(0,1)和满足(2)和(3)式的ρ,σ,φ∈R，如果存在矩阵L∈Rn×p，正定矩阵P1,P2∈Rn×n和标量εij>0，ηij>0,i,j=1,2，使得下面的矩阵不等式成立：

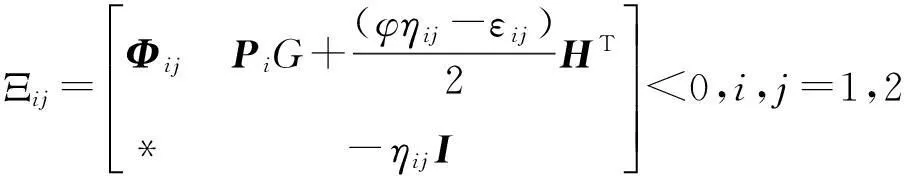
(10)

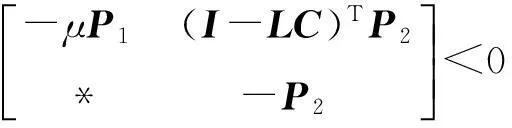
(11)

其中:

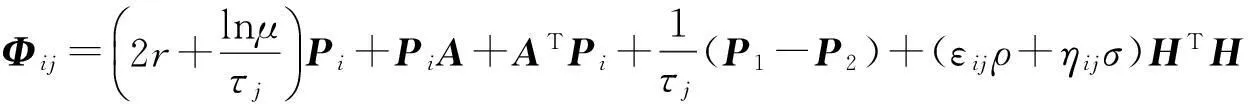
则误差系统(5)在S(τ1,τ2)上全局指数稳定。

证明记ρi≜ρi(t),i=0,1,2，则由ρi的定义和矩阵不等式(10)的可行性，有:

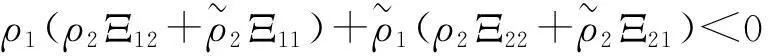
上式等价于:

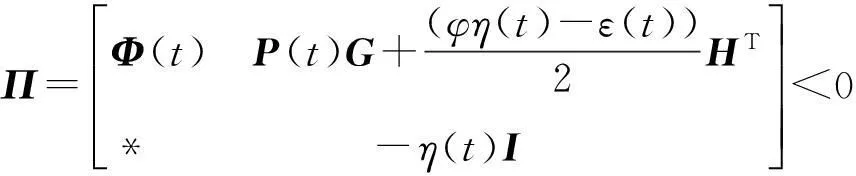
(12)

其中:

Φ(t)=(2r+ρ0(t)lnμ)P(t)+P(t)A+ATP(t)+ρ0(t)(P1-P2)+(ε(t)ρ+η(t)σ)HTH，

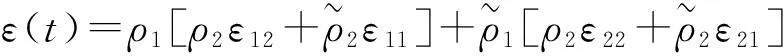
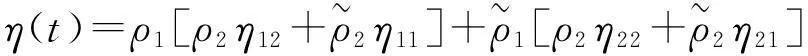
选取Laypunov函数如式(9)所定义，并记V(t)≜V(t,e(t))，则当t∈[tk,tk+1)时，有:

2μρ1eT(t)P(t)GΔf(t)-2rV(t)。

(13)

另由式(2)，有ρeT(t)HTHe(t)-eT(t)HTΔf(t)≥0。从而，对任意μ∈(0,1)及εij>0，有:

μρ1ε(t)[ρeT(t)HTHe(t)-eT(t)HTΔf(t)]≥0。

(14)

类似地，对任意μ∈(0,1)及ηij>0，由式(3)有：

μρ1η(t)[σeT(t)HTHe(t)+φeT(t)HTΔf(t)-ΔfT(t)Δf(t)]≥0。

(15)

将式(14)和式(15)加到式(13)，得：

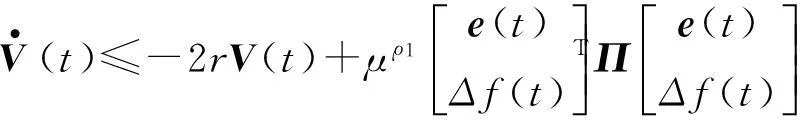
(16)

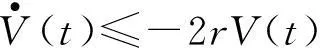
V(t)≤V(tk)e-2r(t-tk)t∈[tk,tk+1)。

(17)

另一方面，由式(11)的可行性并利用Schur补，有:

(I-LC)TP2(I-LC)≤μP1，

(18)

从而，在脉冲发生时间点t=tk处，有:

(19)

对任意给定的t≥t0，必定存在k∈N0，使得t∈[tk,tk+1)。联合式(17)和式(19)，可得：

V(tk-1)exp(-2r(t-tk-1))≤…≤V(t0)exp(-2r(t-t0))。

(20)

另由V(t)定义知，对∀t≥t0有：

μλ1‖e(t)‖2≤V(t)≤λ2‖e(t)‖2，

(21)

其中，λ1=min{λmin(Pi);i=1,2}，λ2=max{λmax(Pi);i=1,2}。从而由式(20)及式(21)得：

(22)

即观测误差系统(5)全局指数稳定。

注2：误差系统(5)稳定性条件的推导基于时变Laypunov函数(9)和系统的单边Lipschitz条件(2)和(3)。一方面，由于时变Laypunov函数包含了脉冲发生时刻，这有助于充分利用混杂系统(5)的信息，能得到具有更少保守性的结果。另一方面，如注1如述，单边Lipschitz条件包含了传统的Lipschitz条件，故定理1所得结果会具有更广的适用范围。

采用线性矩阵不等式技术将式(11)线性化，可得观测器增益矩阵L的求解方法。

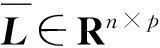
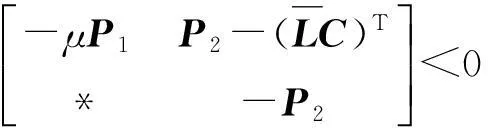
(23)

注3：定理1和定理2中的参数μ的选取依赖于被观测系统的参数设置。注意到对任意给定的μ∈(0,1)和r>0，不等式(10)和(23)为线性矩阵不等式，从而可由matlab线性矩阵不等式工具箱求解。因此，μ可通过一维搜索确定，即给定r>0，在μ∈(0,1)上利用简单的一维搜索确定使得线性矩阵不等式(10)和(23)存在可行解的参数值μ。

特殊地，当脉冲发生间隔相等，即τ1=τ2=τ时，容易由定理2得到下面的推论1。

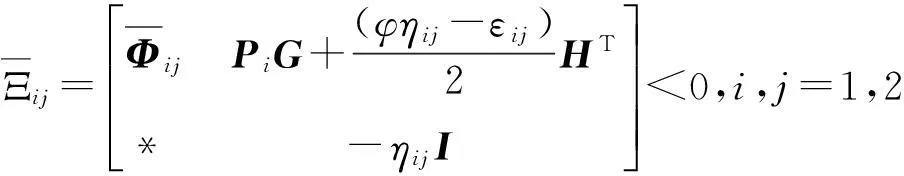
(24)

其中:

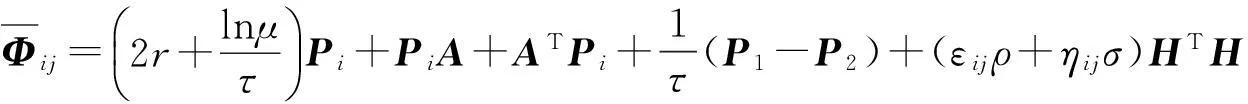
另外，当选取P1=P2=P时，也容易由定理2得到下面的推论2。

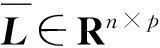
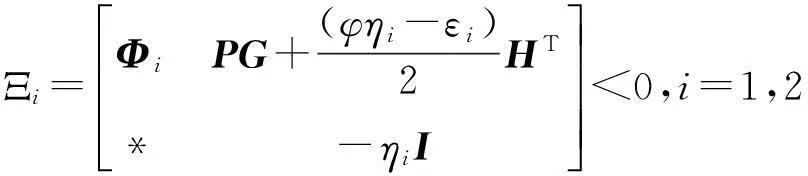
(25)

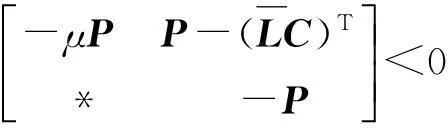
(26)

其中：

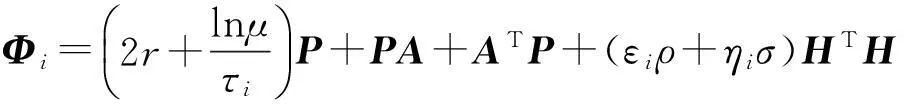
证明在定理2的证明中选取Pi=P，εij=εi，ηij=ηi，i=1,2可得推论2成立。

3实例分析与仿真

下面给出两个例子的观测器设计和仿真用以说明了本文所提方法的可行性。

例1考虑一个机械手臂模型，其系统结构可用式(1)表示，其中:

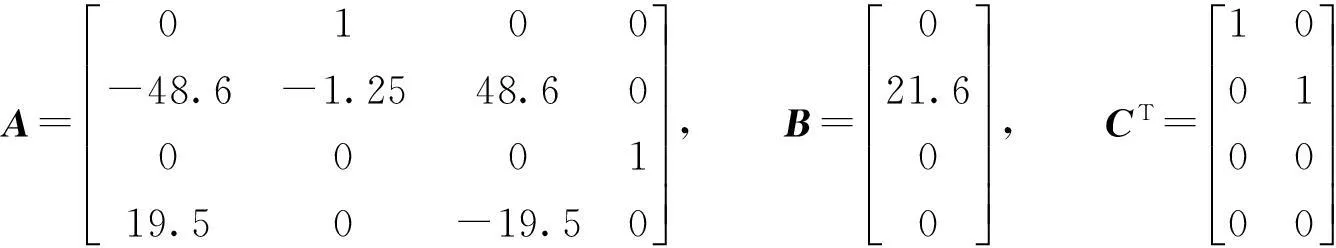
GT=[000-3.33], H=[0010],f(x)=sinx。

易知f(x)满足Lipschitz条件，其Lipschitz常数为lf=1。而当选取ρ=1,σ=1,φ=0时，可以验证f(x)满足条件①和②，故可以运用定理2设计例1的脉冲观测器。假设脉冲序列{tk}∈S(0.001,0.200)，取μ=0.963，用matlab软件求解矩阵不等式(10)和式(23)，得相应的观测器反馈增益矩阵为：

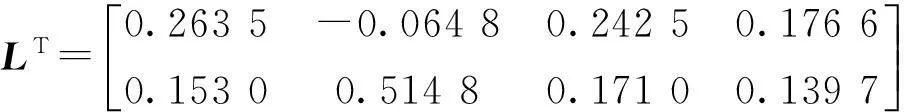
例2考虑一个输入为零的非线性系统(1)，其中:

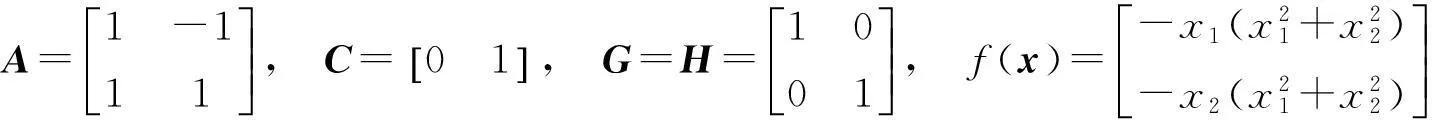
由文献[17]的讨论知，例2的系统为单边Lipschitz非线性系统，其单边Lipschitz常数可取为ρ=0。且使该系统满足条件(b)的σ和φ的取值范围为:

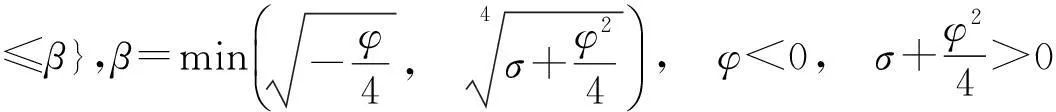
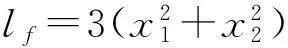
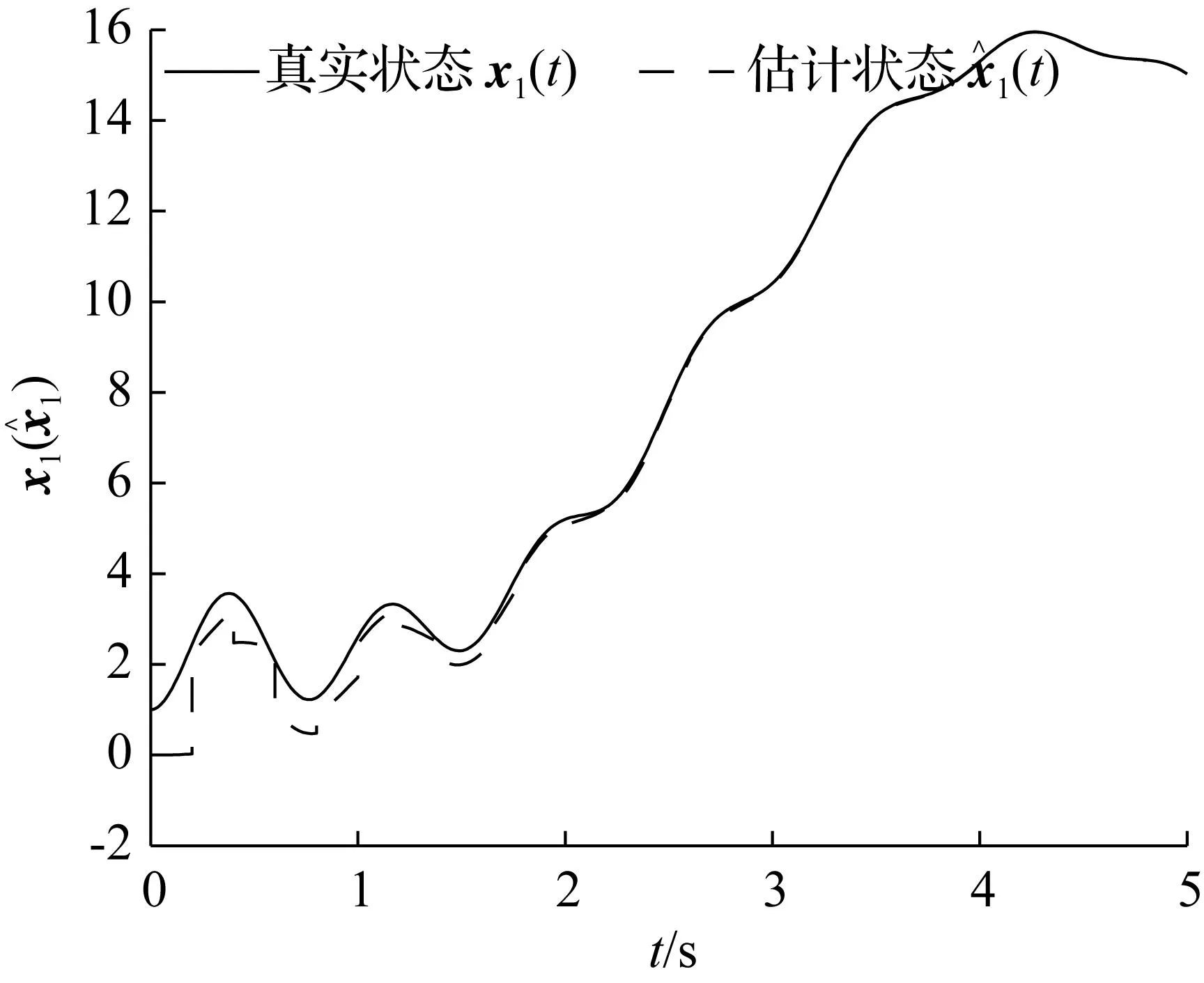
图1{tk}∈S(0.001,0.2)时，x1(t)及x^1(t)变化情况

Fig.1x1(t) andx^1(t) in case {tk}∈S(0.001,0.2)

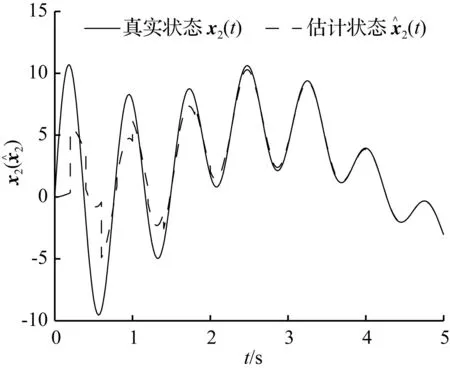
图2{tk}∈S(0.001,0.2)时，x2(t)及x^2(t)变化情况

Fig.2x2(t) andx^2(t) in case {tk}∈S(0.001,0.2)

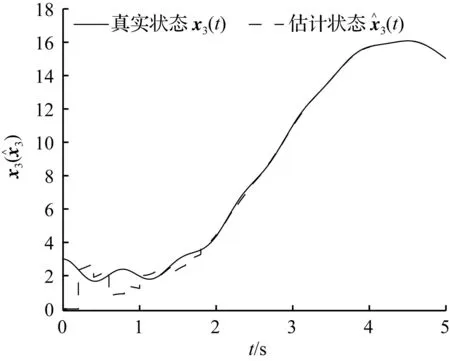
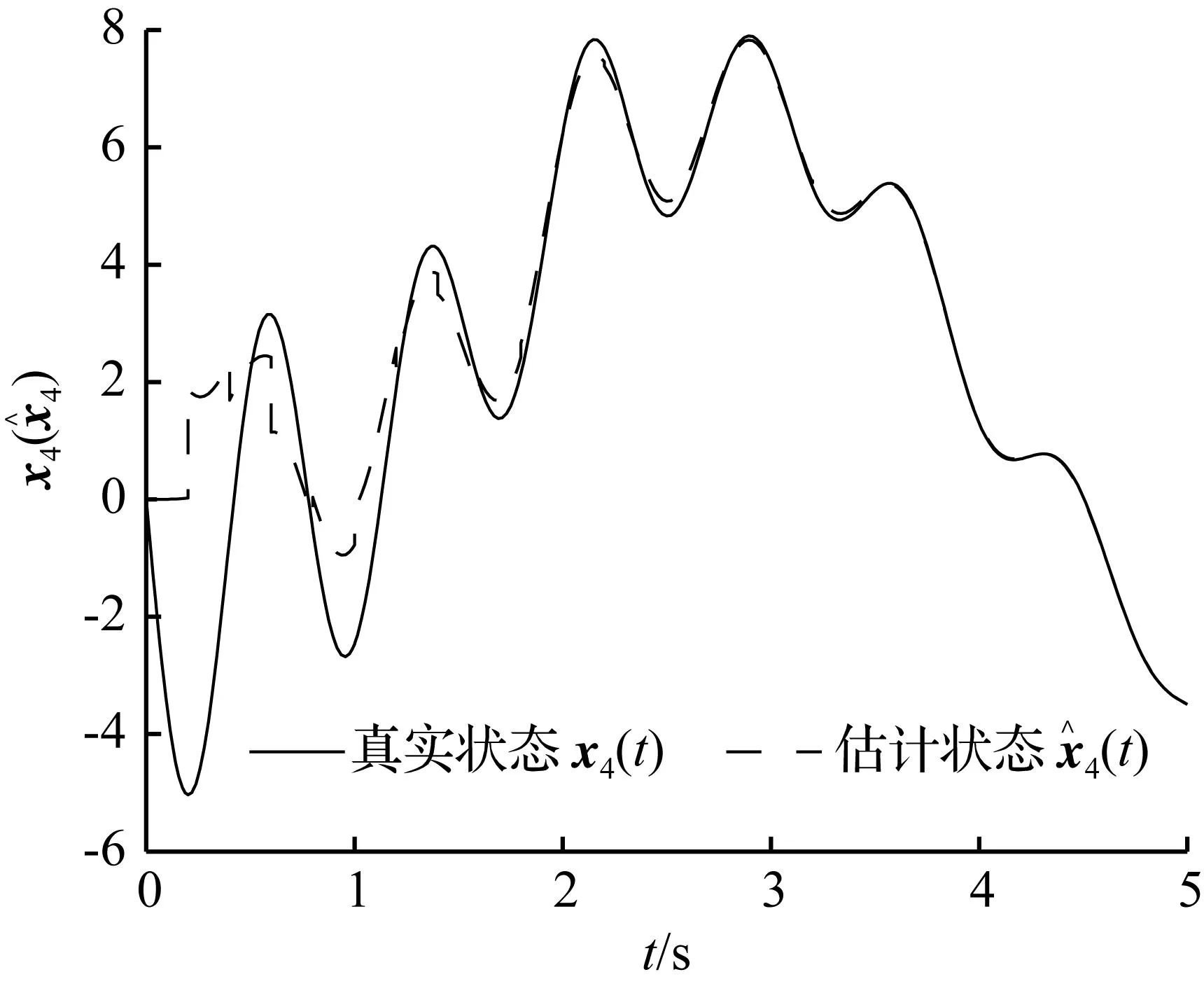
图4{tk}∈S(0.001,0.2)时，x4(t)及x^4(t)变化情况

Fig.4x4(t) andx^4(t) in case {tk}∈S(0.001,0.2)

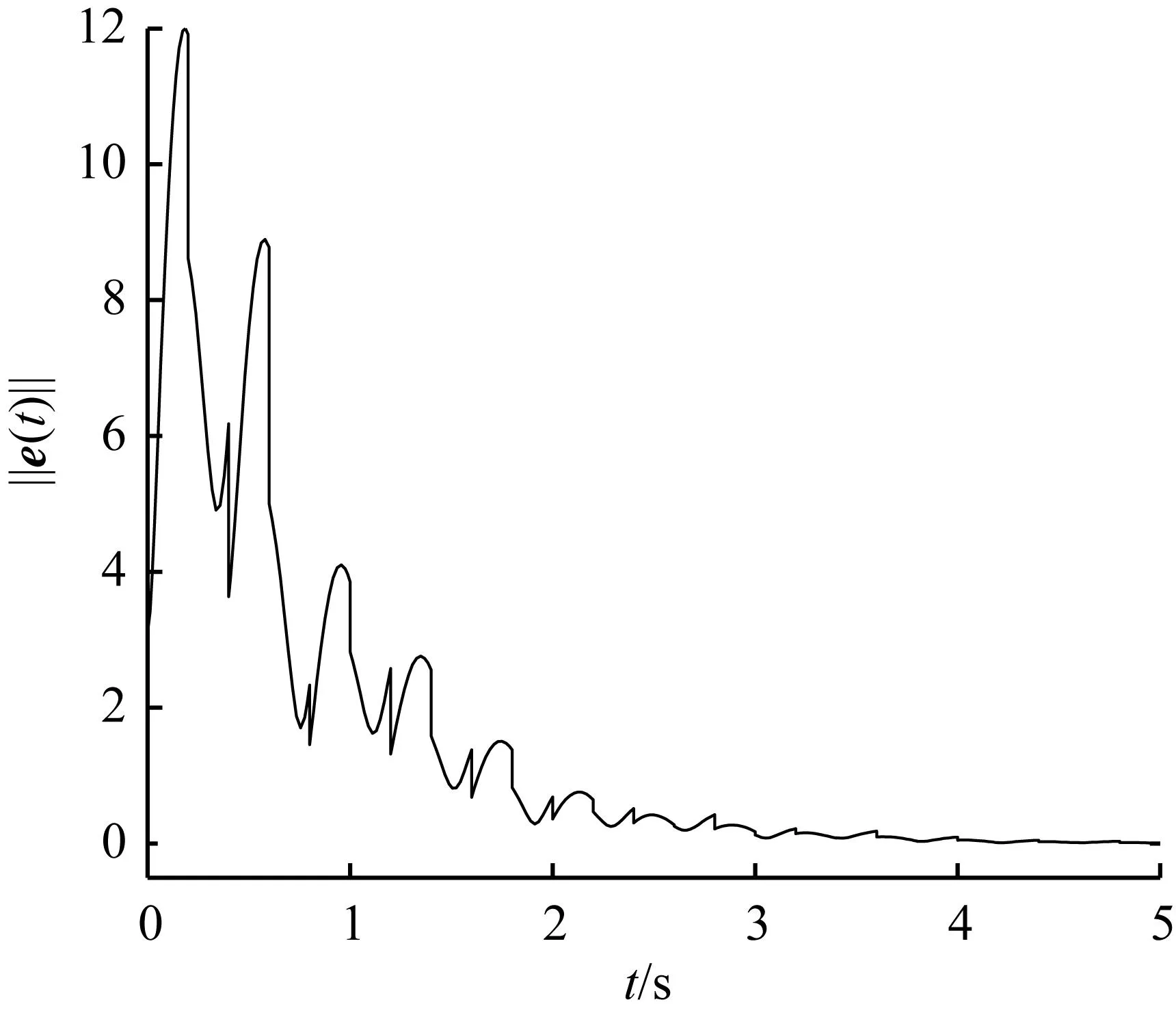
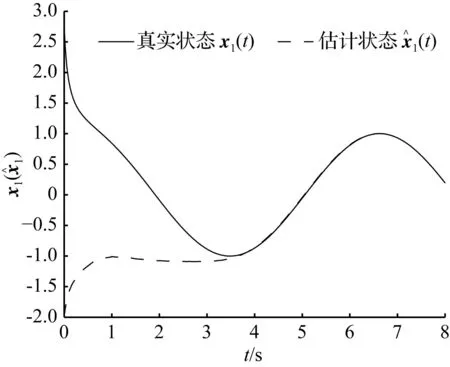
图6{tk}∈S(0.001,0.25)时，x1(t)及x^1(t)变化情况

Fig.6x1(t) andx^1(t) in case {tk}∈S(0.001,0.25)

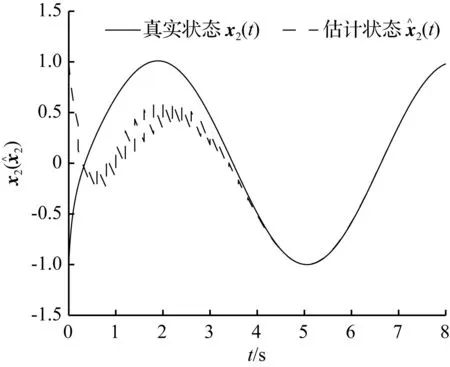
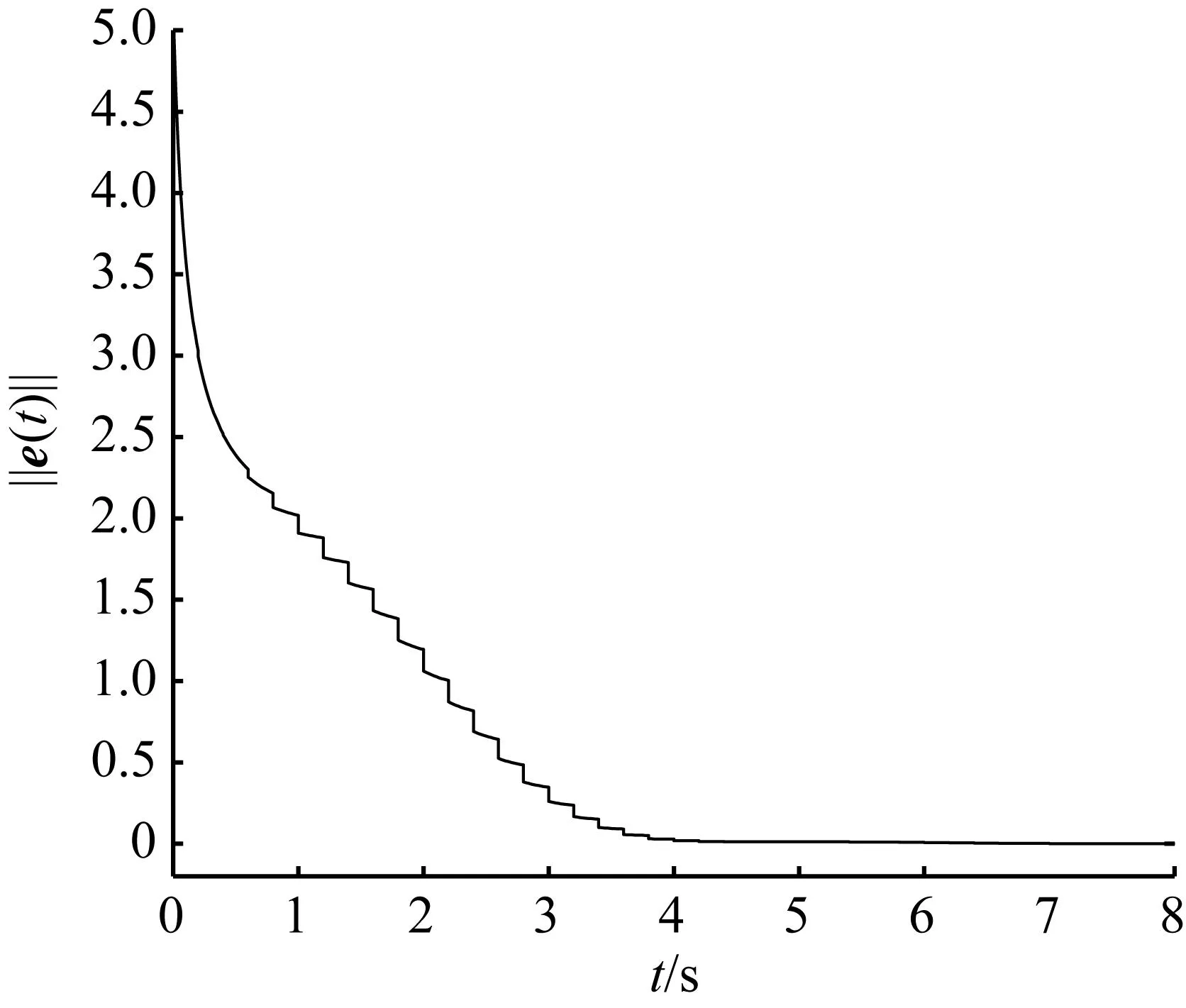
图8{tk}∈S(0.001,0.25)时误差范数‖e(t)‖

Fig.8Norm‖e(t)‖ in case {tk}∈S(0.001,0.25)

4结语

本文采用Laypunov函数方法结合线性矩阵不等式技术和凸组合技术对一类单边Lipschitz非线性系统设计了脉冲观测器。理论分析和仿真结果表明，时变Laypunov函数能更好地刻画脉冲观测器所具有连续和离散混杂的动态特征，而基于单边Lipschitz 条件的观测器设计方法也比基于一般的Lipschitz 条件所得的方法具有更广的适用范围。如何选择适当的随机变量或随机过程刻画脉冲发生时刻，并基于此设计观测器将是下一步研究的方向。

参考文献:

[1]THAU F E.Observing the state of nonlinear dynamic systems [J]. International Journal of Control,1973,17(3):471-479.

[2]KRENER A J, ISIDORI A.Linearization by output injection and nonlinear observers [J]. Systems & Control Letters, 1983, 3 (1): 47-52.

[3]ZEITZ M.The Extended Luenberger observers for nonlinear systems [J]. Systems & Control Letters,1987,9(3):149-156.

[4]SORENSON H W.Kalman-filtering: theory and application [M]. New York: IEEE Press, 1985.

[5]李繁飙，石碰，苏晓杰.不确定半马尔可夫跳变系统的滑模观测器设计[J]. 系统科学与数学, 2014, 34 (10): 1233-1243.

[6]LENDEK Z, LAUBER J, GUERRA T M, et al.Adaptive observers for TS fuzzy systems with unknown polynomial inputs [J]. Fuzzy Sets and Systems, 2010, 161 (15): 2043-2065.

[7]杨冬梅，张静.不确定时滞Lur’e控制系统的鲁棒H∞观测器设计[J]. 东北大学学报: 自然科学版, 2013, 34 (3): 305-307, 325.

[8]LI X, XIANG Z G.Observer design of discrete-time impulsive switched nonlinear systems with time-varying delays [J]. Applied Mathematics and Computation, 2014, 229: 327-339.

[9]ZEMOUCHE A, BOUTAYEB M.A unifiedH∞adaptive observer synthesis method for a class of systems with both Lipschitz and monotone nonlinearities [J]. Systems & Control Letters, 2009, 58 (4): 282-288.

[10]MOISANA M, BERNARD O.Robust interval observers for global Lipschitz uncertain chaotic systems [J]. Systems & Control Letters, 2010, 59 (11): 687-694.

[11]EFIMOV D, FRIDMAN L.Global sliding-mode observer with adjusted gains for locally Lipschitz systems [J]. Automatica, 2011, 47 (3): 565-570.

[12]EKRAMIAN M, SHEIKHOLESLAM F, HOSSEINNIA S, et al.Adaptive state observer for Lipschitz nonlinear systems [J]. Systems & Control Letters, 2013, 62 (4): 319-323.

[13]RAFF T, ALLGOWER F.Observers with impulsive dynamical behavior for linear and nonlinear continuous-time systems [C]. in Proceedings of the 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, December 2007: 4287-4292.

[14]CHEN W H, LU X M.Comments on Designing a novel adaptive impulsive observer for nolinear continuous systems using LMIs [J]. IEEE Transactions on Circuits and Systems I, 2013, 60 (4): 1094-1096.

[15]CHEN W H, LI D X, LU X M.Impulsiver observers with variable update intervals for Lipschitz nonlinear time delays systems [J]. International Journal of Systems Science, 2013, 44 (10): 1934-1947.

[16]陈武华，杨武，黄敢基.基于脉冲观测器的连续时间系统输出反馈镇定[J]. 广西大学学报: 自然科学版, 2013, 38 (2): 987-993.

[17]ABBASZADEH M, MARQUEZ H J.Nonlinear observer design for one-sided Lipschitz systems [C]. in Proceedings of the American Control Conference, Marriott Waterfront Baltimore, MD, USA, 2010: 5284-5289.

[18]DEKKER K, VERWER J G.Stability of Runge-Kutta Methods for Stiff Nonlinear Differential Equations [M]. North-Holland, Amsterdam, 1984.

[19]ZHANG W, SU H, WANG H, et al.Full-order and reduced-order observers for one-sided Lipschitz nonlinear systems using Riccati equations [J]. Commun Nonlinear Sci Numer Simulat, 2012, 17: 4968-4977.

[20]ZHANG W, SU H, SU S, et al.Nonlinear H∞observer design for one-sided Lipschitz systems [J]. Neurocomputing, 2014, 145: 505-511.

(责任编辑梁碧芬)

Impulsive observer design for a class of one-sided Lipschitz system

HUANG Gan-ji, LUO Shi-xian, WEI Lin-na, CHEN Wu-hua

(College of Mathematics and Information Science, Guangxi University, Nanning 530004, China)

Abstract:To investigate the observer design method for a class of one-sided Lipschitz nonlinear system, an impulsive instant-related time varying Lyapunov function is constructed to analyze the stability of the error system, combining linear matrix inequalities technology and one-sided Lipschitz condition, sufficient condition for the exponentially converge of the observer and the solution of the observer gain matrix are then obtained. The results show that the effect of impulsive on stability of error system can be dealt with effectively by using the time varying Lyapunov function, and the one-sided Lipschitz condition based observer possesses wider application scope compared to the traditional Lipschitz condition based observer.

Key words:one-sided Lipschitz system; time-varying Lyapunov functions; impulsive observer; exponential stability

中图分类号：O231

文献标识码：A

文章编号：1001-7445(2015)06-1588-09

doi:10.13624/j.cnki.issn.1001-7445.2015.1588

通讯作者：黄敢基(1972—)，男，广西钦州人，广西大学副教授； E-mail: ganjih@163.com。

基金项目：国家自然科学基金项目(61573111;61164016)；广西自然科学基金重点项目(2013GXNSFDA019003)；广西大学自然科学基金项目(XJZ110626);广西研究生教育创新计划资助项目(YCSZ2015031)

收稿日期：2015-08-21；

修订日期：2015-09-25