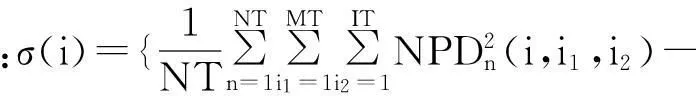一种基于蒙特卡罗算法的微观人口仿真

一种基于蒙特卡罗算法的微观人口仿真

赵志鹏, 张浩军, 王欲听

(河南工业大学， 郑州 450001)

摘要：马尔科夫链·蒙特卡罗(MCMC)方法使用服从某种概率分布的随机数来仿真系统中可能出现的随机现象。将MCMC思想应用于人口微观仿真系统中，提出了一种基于蒙特卡罗算法的微观人口仿真模型，建立了对应的概率分布函数，设计了一种基于蒙特卡罗随机数原理的抽样算法，并在Wolfram mathematica平台上对其进行模拟实验，仿真出河南省2015-2050年间人口变化曲线，并对仿真误差进行分析。结果表明，该算法能够有效仿真人口变化规律，对人口个体微观变化过程的研究具有重要作用。

关键词：蒙特卡罗方法；概率分布函数；人口微观仿真

收稿日期：2015-05-04

基金项目：国家自然科学基金项目(U1304606)；国家863高技术研究发展计划(2012AA101608)

作者简介：赵志鹏(1991-)，女，河南洛阳人，硕士生，主要研究方向为数据处理。

文章编号：1671-6906(2015)04-0050-05

中图分类号：TP274

文献标志码：A

DOI:10.3969/j.issn.1671-6906.2015.04.013

Abstract:The essence of Markov Chain Monte Carlo(referred to as MCMC) method is used to obey a certain distribution of random number to simulate random phenomena that may occur in the system. In this paper, the ideas are transplanted to the population microscopic simulation system. A micro population simulation model is proposed based on Monte Carlo method, and probability distribution function is established. An sampling algorithm is designed based on Monte Carlo random numbers principle and a simulative experiment is made in Wolfram mathematica platform and population varying curve is simulated from 2015 to 2050 in Henan province. Then the error of the simulation is analyzed, which shows the algorithm can effectively simulate laws for the population development and makes a significant contribution to the study of population individuals micro change process.

微观仿真(micro-simulation)一般适用于难以用数学方法解答的复杂组成系统中个体之间交互过程的研究[1]，40多年来得到了快速的发展。齐险峰等提出了人口微观仿真模型，对人口微观仿真领域做出了突出贡献,但未给出技术细节及仿真结果[2]。杨朝勇在队列要素法人口预测基础上提出改进的队列要素法，其更加符合人口变化的实际情况，但预测结果精度有限[3]。

本文提出了基于蒙特卡罗算法的人口预测微观仿真模型，建立了人口学相关要素的概率分布函数，即年龄概率分布函数、预测年的死亡概率分布函数及预测年育龄妇女的生育概率分布函数等，设计了基于蒙特卡罗随机数原理的抽样算法，并进行了仿真实验，结果显示预测精度较高。

1蒙特卡罗方法具体应用过程

应用蒙特卡罗方法模拟人口变化过程的基本思想是：首先根据已有数据建立符合人口发展规律的概率模型，产生符合要求的抽样随机数，最后用随机数对已知的人口随机参数进行抽样，计算求解。

2仿真模型与概率分布函数

2.1建立仿真模型

人口仿真模型由仿真时钟[4]、年龄仿真[5]、死亡仿真[6]和生育仿真[2]组成，如图1所示。

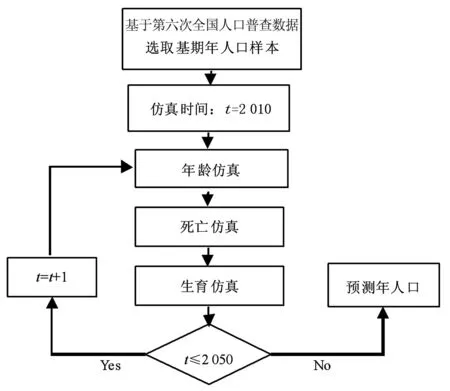
图1　人口微观仿真模型框架

2.2建立概率分布函数

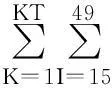
3仿真流程

3.1年龄仿真

根据表1中的年龄概率分布函数值，基于蒙特卡罗方法[8-9]设计了一种年龄仿真算法，如下所示：

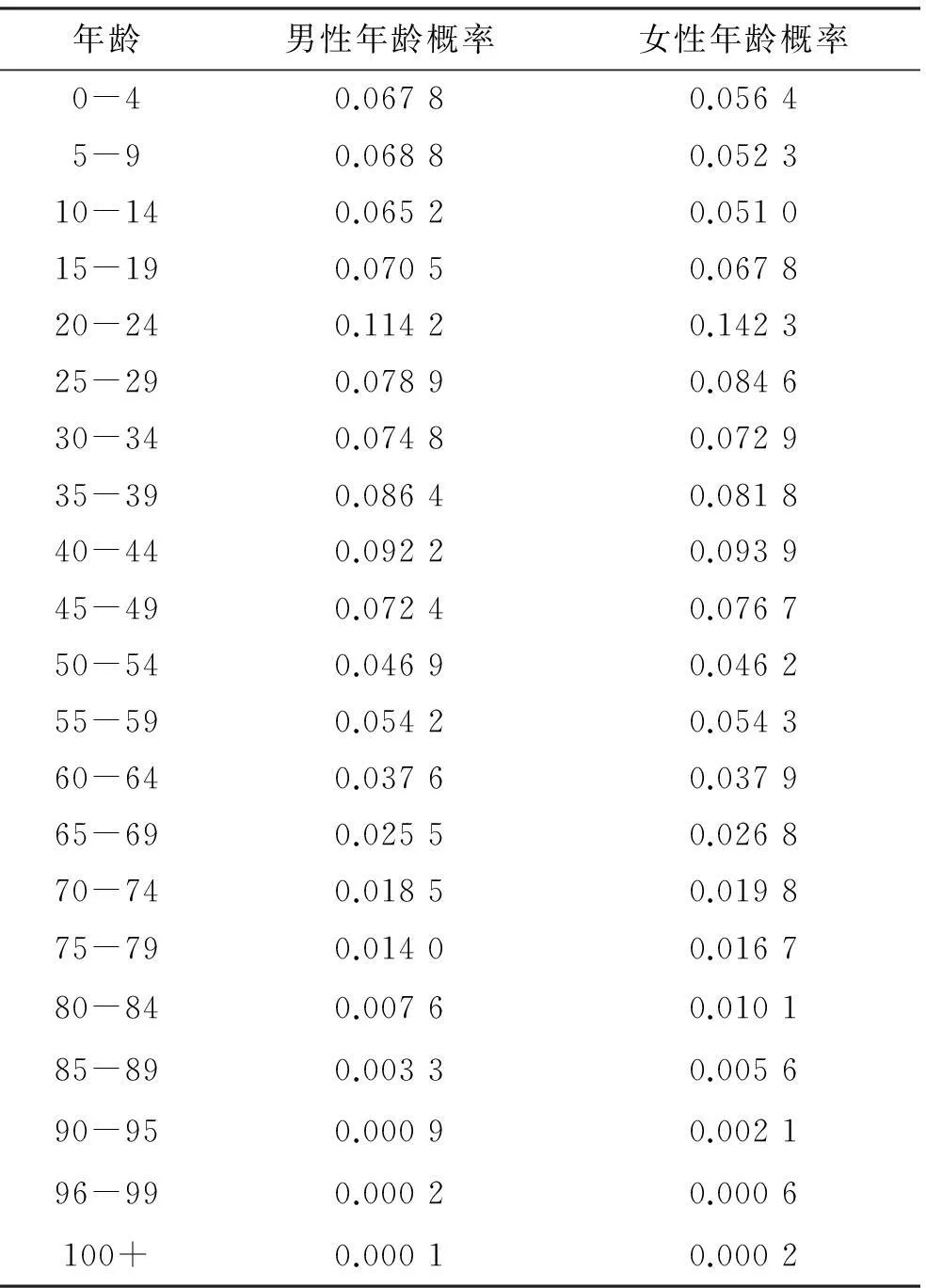
表1　2010年男/女年龄概率分布表

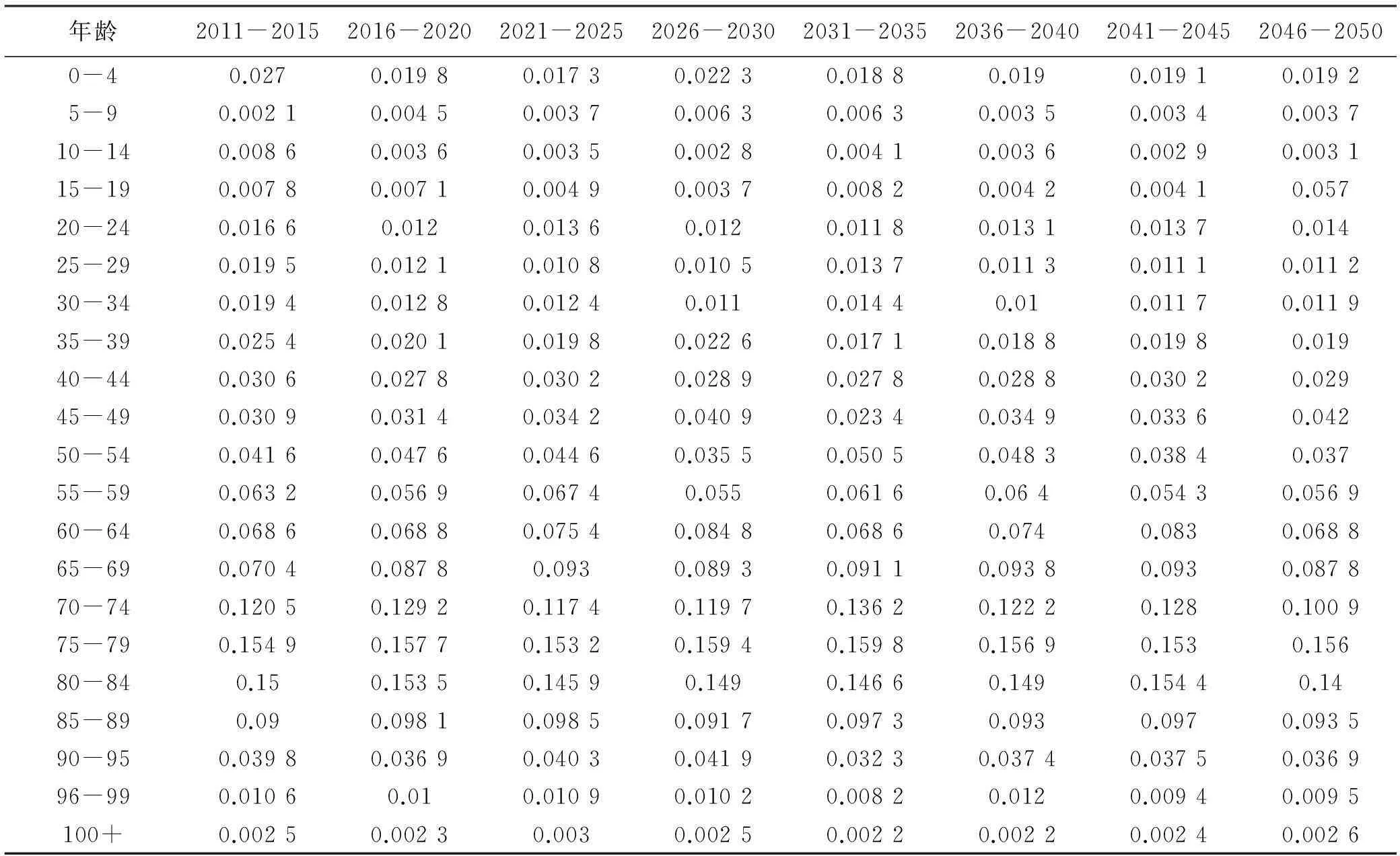
表2　2011-2050预测年死亡概率分布表

表3　2011-2050预测年育龄妇女生育概率分布表

第一步：产生随机数R，0≤R≤1；

第二步：令x=0，F=F(0)；

第三步：当x≤W时，执行第四步；

第四步：若R

第五步：x=x+1，F=F+F(x)，转到第三步；

第六步：年龄抽样结束。

3.2死亡仿真

根据表2中的死亡概率分布函数值，基于蒙特卡罗方法设计了一种死亡仿真算法，如下所示：

第一步：产生随机数R，0≤R≤1；

第二步：令x=0，F=F(0)；

第三步：当x≤W时，执行第四步；

第四步：若R

第五步：x=x+1，F=F+F(x)，转到第三步：

第六步：死亡抽样结束。

3.3生育仿真

根据表3中的生育概率分布函数值，基于蒙特卡罗方法设计了一种生育仿真算法，如下所示：

第一步：产生随机数R，0≤R≤1；

第二步：令x=0，F=F(0)；

第三步：当x≤W时，执行第四步；

第四步：若R

第五步：x=x+1，F=F+F(x)，转到第三步：

第六步：生育抽样结束。

4仿真结果

4.1总人口、死亡人口及出生人口仿真结果

经过上百万次计算机对人口仿真的模拟，得出河南省2010-2050年的总人口、死亡人口及出生人口变化趋势，如图2所示。

从图2可以看出，2010-2040年间河南省总人口数量大约为指数增长，2040-2050年河南省总人口大约为负增长；2010-2050年间河南省死亡人数大约为指数形式逐年增长；2010-2040年间出生人数近似为指数下降，2040-2050年间出生人口数近似为平稳状态。

4.2仿真结果与队列要素方法结果对比

对蒙特卡罗仿真结果与队列要素方法预测结果拟合对比可知，两种方法每年总人口预测差值不到0.6%，验证了上述实验的正确性。

5人口仿真模拟的误差分析

MCMC方法是通过对大量人口样本的随机抽样而得到统计结果，因此得到的数字结果实际是不确定的值，即随机过程不可复制[10-11]。因而通过MCMC方法虽可得到每年相关人口数据，但人口数并不是这些确定的数值，而是指在以它为中心左右浮动的一段小空间内的数值。如果把这些点绘制成一条曲线，那么其真正的解就是围绕这条曲线的一条窄带[12]。

通过上述定义可求第i年总死亡率的误差：

(1)

从式(1)可知,εi与NT的平方根的倒数成正比，这表明只要样本的总数不断增大，相对应的误差带宽度就会不断减窄[13]。

6微观仿真的内部变化过程及结论

6.1仿真的内部动态变化过程

微观仿真的最终目标是获得研究系统中个体的内部变化过程，且通过计算机记录它的仿真结果[14]。本文通过对人口年龄的仿真，可以标记出系统中每个个体的年龄大小。对预测年死亡人口的仿真，可以标记出系统中预测期每个个体是否死亡以及详细的死亡年限。对预测年育龄妇女的仿真，可以标记出系统中预测年每个育龄妇女个体的生育年限。

6.2预测出系统中微观个体的存活寿命

通过对基于蒙特卡罗方法的微观仿真结果误差分析，结果表明，本文设计的微观仿真模型及计算机仿真结果正确可信。因此，可以进一步讨论计算机仿真中人口个体特征的变化状况，根据运行程序的年龄仿真模块可以仿真得到系统中每个个体的年龄大小，进入死亡仿真模块后可以仿真出系统中2010-2050年间死亡个体的死亡年限，最后综合这两个模块可以推算出系统中每个个体到2050年的生存寿命，如图3所示。

图3　人口模拟系统中微观个体存活至2050年的寿命

从图3中可以看出，从2010年到2050年，系统中20岁的人有135万，40岁的有150万，60岁的有170万，70岁的有250万，80岁的有150万。可以看出，60～80岁为年龄高峰期。因此，河南省未来40年人口老龄化情况依然严峻，政府需要采取一系列宏观调控措施予以应对。

7结语

本文首先提出基于蒙特卡罗思想的微观人口仿真模型，建立了人口学相关要素的概率分布函数，即年龄概率分布函数、预测年的死亡概率分布函数及预测年育龄妇女的生育概率分布函数。设计了基于蒙特卡罗随机数原理的抽样方法，并在Wolfram mathematica 9.0平台上将此算法经过上百万次的模拟，得出河南省2010-2050年间总人口、死亡人口及出生人口的仿真变化曲线。另外，对仿真误差进行分析可知，随着样本数量的增加，相应的误差会逐渐减少。最后对计算机微观仿真的内部过程进行分析，预测出个体存活寿命。

参考文献：

[1]邹振宇．交通系统的微观仿真及其参数校正研究[D]．杭州：浙江大学，2006．

[2]齐险峰，郭震威．“四二一”家庭微观仿真模型与应用[J]．人口研究，2007，5(3)：1-8．

[3]杨朝勇．队列要素法与浙江省人口预测[D]．杭州：浙江大学，2003．

[4]米红，肖利群．蒙特卡罗方法在总和生育率计算中的应用[D]．厦门：厦门大学，2008．

[5]杨耀臣. 马尔可夫链-蒙特卡罗方法与人口学研究[D]．合肥：中国科技大学，2008．

[6]盛骤，谢式千，潘承毅．概率论与数理统计[M]．北京：高等教育出版社，2001：146-147．

[7]Conner J T, Martin R D，Atlas L E. Recurrent Neural Networks and Robust Time Series Prediction[J].IEEE Transactions on Neural Net-works, 1994,5(2):240-254.

[8]Bates J M，Granger C W. Combination of Forecasts[J].Operational Res. Quart,1969,20(4):45-58.

[9]徐钟济．蒙特卡罗方法[M]．上海：上海科学技术出版社，1985：20-100．

[10]Proakis G. Digital Communications(4th)[M]. NewYork:MC Graw-Hill,Inc.USA,2001:7-10.

[11]中国未来人口发展与生育政策研究课题组．中国未来人口发展与生育政策研究[J]．人口研究，2000，3(3)：50-100．

[12]段楠，薛会民，潘越．用蒙特卡洛法计算可靠度时模拟次数的选择[J]．煤矿机械，2002，12(3)：30-36．

[13]Chen J J.2000 Populationcensus of China-Proceedings of International Seminar[J].China Statisties Press,2004,10(4):155-174.

[14]杨耀臣．用蒙特卡罗方法研究肿瘤的放射治疗方案[J]．肿瘤防治研究，1983，24(2)：2-9．

(责任编辑：席艳君)

The Population of the Microscopic Simulation

Based on Monte Carlo Algorithm

ZHAO Zhi-peng, ZHANG Hao-jun, WANG Yu-ting

(Henan University of Technology, Zhengzhou 450001，China)

Key words:Monte Carlo method；probability density function；microscopic simulation population