基于局部密度的高效聚类算法研究

周　杰，刘立波，卜旭松

(宁夏大学 数学计算机学院，宁夏 银川 750021)

基于局部密度的高效聚类算法研究

周杰，刘立波，卜旭松

(宁夏大学 数学计算机学院，宁夏 银川 750021)

摘要：针对基于密度聚类算法对参数值过于敏感、参数值难以设置的不足，提出一种基于局部密度的高效聚类算法，以有效解决基于密度聚类算法对密度层级不同数据集聚类准确率低的问题。该算法将局部密度概念和k-means算法相结合，在算法迭代过程中动态计算局部密度参数和簇核心距。对于分布在簇核心距之内的数据，采用基于划分的方法直接聚类；对于分布在簇核心距之外的数据采用基于局部密度方法进行聚类。实验结果表明，提出的算法在聚类精度和计算效率两方面均具有较好的性能。

关键词：k-means；局部密度；簇核心距；聚类

中图分类号：TP391

文献标志码：码：A

文章编号：号：2095-4824(2015)06-0021-05

收稿日期：2015-09-11

作者简介：周杰(1990-)，女，宁夏银川人，宁夏大学数学计算机学院硕士研究生。

Abstract：In view of the limitation of density-based clustering algorithm that is sensitive to parameter settings and difficult to set the parameters, this paper proposes an efficient local density-based clustering algorithm for the problem that the density-based clustering algorithm is not accurate to the data set with different density-levels. The proposed algorithm combines the local density concepts and K-means algorithms and dynamically calculates the local-density parameters and core-distance of the clusters in the process of the iteration. The data inside the core-distance is clustered into the clusters directly by the partition-based method and the data outside the core distance of the clusters is clustered by the local density method. Experimental results indicate that the proposed method exhibits better performance in both efficiency and accuracy.

聚类[1-2]作为一种有效的数据挖掘工具已经成功应用于许多领域，如网络安全[3]、生物学、商务智能和Web搜索等多个方面。聚类是把一个数据集划分成多个组或簇的过程，使得簇内高度相似，而簇间相异。若待分类数据集中不含噪声数据，采用基于划分的聚类算法具有较好的聚类效果，但当数据集中存在较多噪声数据时，基于划分的聚类算法聚类质量较低[4-5]。尽管基于密度的聚类算法能通过设置全局阈值方式消除噪声数据对聚类准确率的影响[6-8]，但全局密度阈值不能很好地刻画数据集的内在聚类结构，当数据集中簇的密度层级相差较大时，全局密度阈值选择非常困难，使得聚类质量难以保证。较大的密度阈值能较好地过滤噪声，但容易导致稠密度较小簇中的大量数据被标记为噪声，而较小的密度阈值又会降低算法噪声过滤能力，导致簇中含有较多噪声数据[9]。针对上述问题，本文提出一种基于局部密度聚类的新算法，该算法能有效地解决基于密度聚类算法参数设置难、聚类结果对参数敏感问题，在发现不同密度层级簇方面具有更高的聚类准确率和执行效率。

1相关算法

1.1k-means聚类算法

k-means算法[10-12]首先随机选取k个对象作为算法的初始聚类中心，然后按照某种距离度量公式计算每个对象到各簇聚类中心的距离，将对象划分到离其最近的簇中。重新计算各簇均值，用计算后的簇均值作为新簇聚类中心，重新划分所有对象。迭代继续，直到划分结果稳定，即本次迭代形成的簇与前次迭代形成的簇高度相似。在算法每次迭代过程中，待聚类数据对象只需与k个聚类中心进行比较即可被分配到最相似的簇中，因而算法执行速度快。k-means算法时间复杂度为O(nkt)，其中n表示样本的总个数，t表示迭代次数。采用k-means算法能够实现快速聚类，算法具体过程如下：

Step1：从待聚类的数据集N中随机选取k个对象{m1,m2,m3,…,mk}作为各簇的初始聚类中心；

Step2：repeat；

Step3：对于数据集N中每个对象xi，按照某种距离度量公式计算xi到各聚类中心的距离，将

刘立波(1974-)，女，宁夏银川人，宁夏大学数学计算机学院，博士，教授。

卜旭松(1988-)，男，山东烟台人，宁夏大学数学计算机学院硕士研究生。

xi划分到离其最近的簇中；

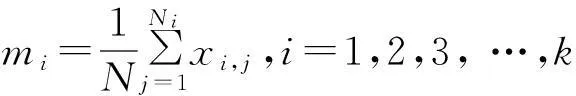
Step5：until聚类中心不发生变化。

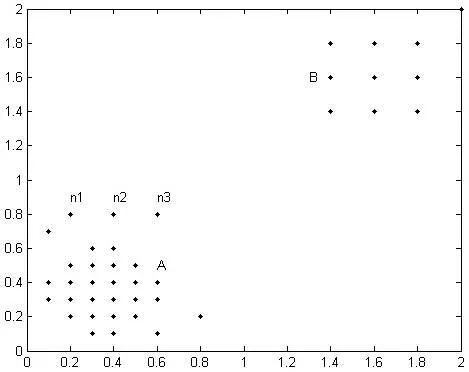
图1　example数据集

图1是example数据集中数据的分布情况，数据集包含簇A和簇B两个密度层级相差较大的簇，n1、n2和n3是噪声数据。

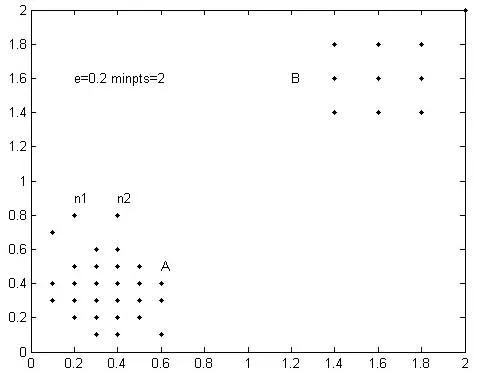
图2　ε=0.2，Minpts=2聚类效果

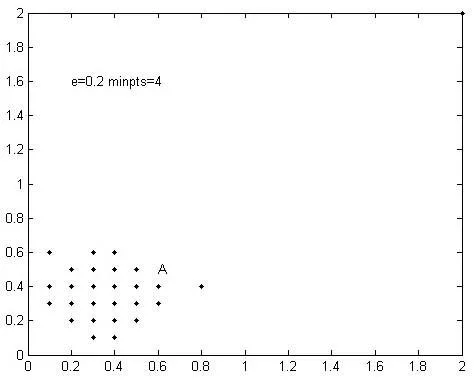
图3　ε=0.2，Minpts=4聚类效果

图2是DBSCAN算法在ε=0.2，Minpts=2时的聚类结果，如图可知算法能准确识别簇B，由于各簇的邻域密度值Minpts均为2，使得局部噪声数据n1、n2等被划分到簇A中，导致簇A聚类不准确。图3是DBSCAN算法在ε=0.2，Minpts=4时的聚类结果，可看出算法能够较准确的识别簇A，由于各簇邻域密度值Minpts均为4，簇B被误标记成噪声数据。

2基于局部密度的聚类算法

k-means算法本身并无过滤噪声和基于局部密度聚类的能力[13-14]。本文将簇稠密度、簇相对稠密度、簇核心距概念和局部密度阈值方法引入到k-means算法中，使算法不仅能够过滤噪声，而且具有基于局部密度聚类方法的优点。提出的聚类算法需要用户设定3个参数：邻域密度值、ε-邻域值和聚类个数k。在算法初次迭代过程中获取簇核心距、簇稠密度和簇相对稠密度等簇属性，并通过这些属性计算簇局部密度阈值,进而将用户设置的全局密度阈值转化为符合各簇密度层级的局部密度阈值。算法在后续迭代过程中通过如下方式过滤噪声进行聚类：

对于待聚类对象xi，若xi离簇Ci距离最近且xi是Ci的核心对象，则直接把xi划分到簇Ci；若xi不是Ci的核心对象，则查找xi的ε-邻域内是否包含RMinpts个对象。若包含RMinpts个对象，则将xi划分到簇Ci，否则将xi标记为噪声。算法每次迭代结束后，重新计算簇Ci的新聚类中心、簇稠密度和相对稠密度，更新簇局部密度阈值。算法继续迭代，直到各簇不再发生变化。以下是本文涉及到的概念、局部密度阈值计算方法和算法具体描述。

2.1相关概念

2.1.1欧氏距离

设xi=(xi1,xi2,xi3,…,xip)和xj=(xj1,xj2,xj3,…,xjp)是两个包含p个数值属性描述的对象。对象xi和xj之间的欧氏距离定义为：

(1)

2.1.2簇核心距

设簇Ci中对象到簇心的欧式距离期望为μi，标准差σi，簇Ci的簇核心距定义为： R(Ci)=μi，若对象xi到簇Ci的欧式距离d(xi,oi)≤R(Ci),则称xi为簇Ci的核心对象。

2.1.3ε-邻域

设xi为数据集N中的对象，xi的ε-邻域是以xi为中心，以ε为半径的空间。

2.1.4邻域密度

对象xi的ε-邻域内包含其他对象的数量。

2.1.5簇稠密度

设Ni是簇Ci当前对象总个数，簇Ci的簇稠密度定义为：

den(Ci)= Ni∕(μi+2σi)，i=1,2,…,k(2)

2.1.6相对稠密度

设簇Ci的稠密度denmax(Ci)=max{den(Ci)}，簇相对稠密度定义如下：

(3)

2.2局部密度阈值计算方法

按照2.1中簇稠密度的定义，首先计算各簇稠密度，再根据簇稠密度计算簇相对稠密度，以簇相对稠密度和用户设定的邻域密度参数的乘积作为簇的局部密度阈值，定义为RMinpts=「Minpst×rden(Ci)⎤。局部密度阈值RMinpts以簇相对密度作为权重计算得出，因而能够较真实地反映各簇密度层级。

2.3算法描述

输入：

k：预期分簇数量。

D：包含n个对象的待聚类数据集。

ε：半径参数。

Minpts：邻域密度阈值。

输出：

基于局部密度的k个簇的集合。

步骤：

Step1：从待聚类的数据集N中随机选取k个对象{m1,m2,m3,…,mk}作为各簇初始聚类中心；

Step2：repeat；

Step3：if (第一次迭代){对于数据集N中的每个对象xi，按照欧式距离度量公式计算xi到各聚类中心距离，将xi划分到离它最近的簇中；}

else {对于数据集N中的每个对象xi，按照欧氏距离计算xi到各聚类中心距离，找出离xi最近的簇Ci。

if (dist(xi,oi)≤R(Ci)){直接将xi划分到簇Ci}

else if (dist(xi,oi)>R(Ci) andxi的ε-邻域包含对象数不小于RMinpts){将xi划分到簇Ci}

else { 将xi标记为噪声}

}

Step4：重新计算簇Ci的新聚类中心；计算簇Ci中对象xi到簇聚类中心oi的欧式距离期望μi和标准差σi；

Step5：until不发生变化。

3实验与分析

通过和DBSCAN算法、文献[6]中提出的IDBSCAN算法对比，验证算法的执行效率。以上三种算法均由JAVA语言编程实现。

3.1聚类准确率分析

实验测试数据如图4，数据集共包含3个簇A、B、C和噪声数据，其中簇A和簇B的密度较大，C的密度较小。实验中本文算法和DBSCAN算法ε-邻域值均为0.4。

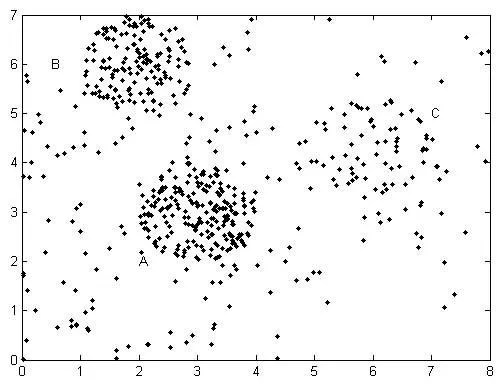
图4　带噪声的数据集

图5是DBSCAN算法在Minpts=10时的聚类效果，图6是DBSCAN算法在Minpts=6时的聚类效果，图7为本算法在Minpts=10时的聚类效果。

图5　DBSCAN算法Minpts=10聚类效果

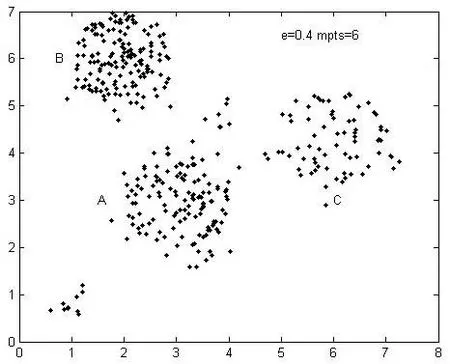
图6　DBSCAN算法Minpts=6聚类效果

从图5可看出，当DBSCAN算法的ε-邻域参数设为0.4，邻域密度参数设为10时，算法能够过滤噪声数据，较准确地对簇A和簇B进行聚类，由于簇C的密度相对较小，因此簇C的部分数据被当作噪声数据过滤掉。从图6可看，出当DBSCAN算法的ε-邻域参数设为0.4，邻域密度参数设为6时，由于邻域密度参数阈值相对较小，簇C能够被较准确地识别，簇A和簇B周围的一些噪声数据被划归到这两个簇中，导致簇A和簇B聚类不准确。

图7　本算法Minpts=10聚类效果图

对比图5和图6，不难发现DBSCAN算法对此类数据聚类的缺点。从图7可以看出，当本算法ε-邻域参数设为0.4，邻域密度参数设为10时，第一次迭代过程中算法计算得到簇A的局部密度阈值RMinptsA=10，簇B的局部密度参数RMinptsB=9，簇C的局部密度参数为RMinptsC=5。这3个簇邻域密度参数能够较好地反映各簇内部结构，聚类过程中算法按照各簇密度阈值过滤噪声数据进行聚类，上述实验结果表明本算法聚类效果比DBSCAN算法更准确。

3.2算法执行效率分析

算法执行效率验证的实验硬件环境为Intel(R) Core(TM) i3-3110M CPU @ 2.4 GHz，内存4 GB。实验选取5个数据集，每个数据集包含两个簇和噪声数据，数据集具体信息如表1所示，本文算法、DBSCAN算法和文献[6]中的IDBSCAN算法的执行效率如图8所示。

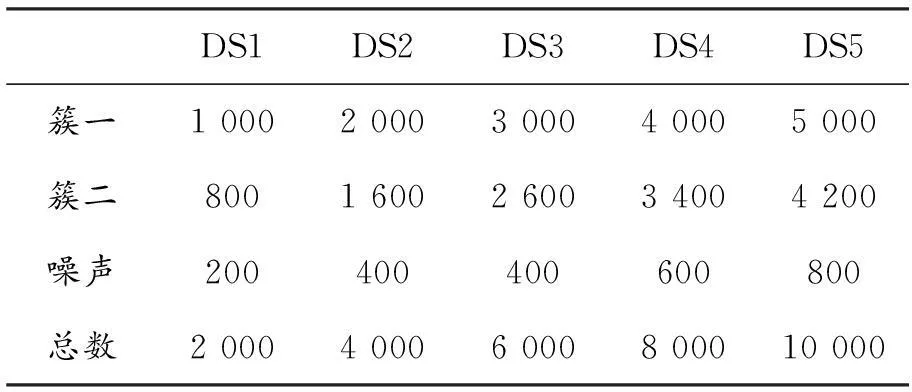
表1　数据集信息

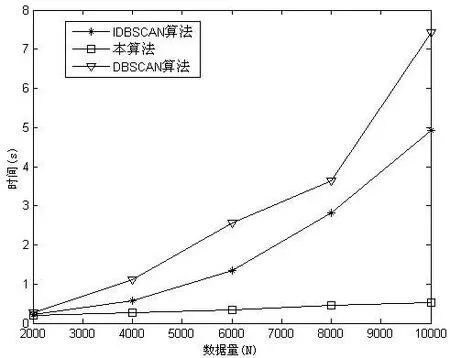
图8　算法执行效率对比

从图8可以看出，由于DBSCAN算法对于每个点都要验证其是否达到邻域密度规定的Minpts个点，算法时间开销较大；IDBSCAN算法避免了邻域内重叠对象的检测，效率有所提升；本文算法只对到簇心距离大于簇核心距的对象进行验证是否满足最小邻域密度要求，所需对象验证数量少，因而算法耗时少，具有比DBSCAN算法和IDBSCAN算法更高的执行效率。

4结语

针对基于密度聚类算法对簇密度层级相差较大的数据集聚类不准确问题，本文将局部密度阈值方法和k-means算法相结合，提出了基于局部密度聚类算法。该算法用局部阈值取代全局阈值进行聚类，更准确地反映数据集内各簇的密度结构。与传统的基于密度的聚类算法相比，本文算法具有更高的聚类准确率和算法执行效率。然而，提出的算法在发掘任意形状簇方面仍存在不足，如何提高它在发掘任意形状簇方面的能力，是本课题组今后的研究方向。

[参考文献]

[1]公茂果，王 爽，马 萌，等.复杂分布数据的二阶段聚类算法[J].软件学报, 2011,22(11):2760-2772.

[2]孙吉贵,刘杰,赵连宇.聚类算法研究[J].软件学报,2008,19(1):48-61.

[3]丁彦，李永忠.基于PCA和半监督聚类的入侵检测算法研究[J].山东大学学报：工学版,2012，42(5):41-46.

[4]郝洪星，朱玉全，陈耿.基于划分和层次的混合动态聚类算法[J].计算机应用研究,2011,28(1):51-54.

[5]Parsons L,Haque E,Liu H.Subspace clustering for high dimensional data:a review[J].SIGKDD Explorations,2004,6(1):90-105.

[6]毕方明，王为奎，陈龙. 基于空间密度的群以噪声发现聚类算法研究[J].南京大学学报：自然科学版，2012,48(4):491-498.

[7]许虎寅,王治和.一种改进的基于密度的聚类算法[J]. 微电子学与计算机,2012,29(2):44-47.

[8]黄德才,吴天虹.基于密度的混合属性数据流聚类算法[J].控制与决策，2010,25(3):416-421.

[9]王晶,夏鲁宁,荆继武.一种基于密度最大值的聚类算法[J].中国科学院研究生院学报,2009,26(4):539-548.

[10]Redmond S J, Heneghan C.A method for initialising the k-means clustering algorithm using Kd-trees[J]. Pattern Recognition Letters,2007,28(8):965-973

[11]Cao F, Liang J, Jiang G.An initialization method for the k-means algorithm using neighborhood model[J].Computers and Mathematics with Applications,2009,58(3):474-483.

[12]杨福萍,王洪国,董树霞,等.基于聚类划分的两阶段离群点检测算法[J].计算机应用研究,2013,30(7):1942-1945.

[13]Miyahara S, Komazaki Y,Miyamoto S.An algorithm combining spectral clustering and DBSCAN for core points[J].Knowledge and Systems Engineering,2014,245(2):21-28.

[14]Tran T N, Klaudia D,Daszykowski M.Revised DBSCAN algorithm to cluster data with dense adjacent clusters[J]. Chemometrics and Intelligent Laboratory Systems,2013,120(2):92-96.

Research on Efficient Clustering Algorithm Based on Local Density

Zhou Jie，Liu Libo，Bu Xusong

(SchoolofMathematicsandComputerScience，NingxiaUniversity，Yinchuan，Ningxia750021，China)

Key Words：k-means; local density; core-distance; clustering

(责任编辑：张凯兵)