Lorenz混沌系统的数据同化方法研究

摆玉龙，尤元红，邵　宇，张转花

(西北师范大学物理与电子工程学院，甘肃兰州　730070)

Lorenz混沌系统的数据同化方法研究

摆玉龙，尤元红，邵宇，张转花

(西北师范大学物理与电子工程学院，甘肃兰州730070)

摘要：利用数据同化方法研究了Lorenz混沌系统中的非线性问题.提出了一种基于Cholesky分解的降秩平方根滤波算法，可以改善数据同化中的滤波发散现象.通过对卡尔曼滤波误差协方差矩阵进行Cholesky分解，降低协方差矩阵的计算量和存储量，提高滤波的收敛速度.在Lorenz混沌系统上研究了降秩平方根滤波的性能，通过敏感性分析试验，讨论了降秩平方根滤波的稳定性，验证了算法的有效性，比较了降秩平方根滤波与集合卡尔曼滤波的同化性能.结果表明，在Lorenz混沌系统的短期预报实验中，降秩平方根滤波的同化性能优于集合卡尔曼滤波.

关键词：Cholesky分解；Lorenz混沌系统；降秩平方根滤波

收稿日期：2015-05-15;修改稿收到日期:2015-09-20

E-mail:yulongbai@gmail.com

基金项目:国家自然科学基金资助项目(41461078)

作者简介：摆玉龙(1973—)，男，甘肃会宁人，教授，硕士研究生导师.主要研究方向为数据同化和参数估计.

中图分类号：TP 309.7

文献标志码：标志码：A

文章编号：章编号：1001-988Ⅹ(2015)06-0044-06

Abstract:Data assimilation methods are used to study the nonlinear problems in Lorenz chaotic system.A reduced rank square root filter algorithm(RRSQRT) based on Cholesky decomposition is proposed,which can alleviate the filtering divergence phenomenon in data assimilation.Using Kalman filtering error covariance matrix Cholesky decomposition,it can reduce the amount of calculation and storage of covariance matrix and improve the convergent speed of filtering.With the Lorenz chaotic system,sensitivity analysis tests are conducted to research the performance of singular square root filter,the stability of the singular square root filter is discussed and the effectiveness of the algorithm is verified.The assimilation performance between RRSQRT and ensemble Kalman filter(EnKF) BFQis compared.The results show that the RRSQRT is better than EnKF in short time forecast experiment with Lorenz chaotic system.

Data assimilation methods research for Lorenz chaotic systems

BAI Yu-long，YOU Yuan-hong，SHAO Yu，ZHANG Zhuan-hua

(College of Physics and Electronic Engineering，Northwest Normal University，Lanzhou 730070，Gansu，China)

Key words:Cholesky decomposition;Lorenz chaotic systems;reduced rank square root filter

Lorenz以著名的Lorenz方程形式给出了混沌系统的实例[1].在耗散系统中，不同的初始条件下，确定性方程的解出现了混沌现象.混沌系统的研究目前包括混沌控制、混沌保密通信和混沌同步研究等[2-3].在混沌控制研究中，大多数的控制方法都是在已知参数的情形下给出的.如果系统的参数未知或者不确定，将会使控制方法失效.数据同化(也称为资料同化)是源自大气和海洋等领域的研究方法，其核心思想是在模式状态预报中引入观测数据，再根据观测数据对模式状态进行更新，提高预报的效率和准确性[4].卡尔曼滤波(Kalman Filter)方法是一种典型的顺序数据同化方法[5].传统卡尔曼滤波需要对其模型算子和观测算子进行线性化，很多研究者提出了卡尔曼滤波的扩展形式，如扩展卡尔曼滤波(EKF)、集合卡尔曼滤波(EnKF)[6]及确定性集合卡尔曼滤波(DEnKF)[7]等.针对EnKF分析过程中低估预报误差协方差导致同化不能有效吸收观测信息，造成滤波发散的问题，Whitaker[8]在2002年提出了无需扰动观测的集合平方根滤波(EnSRF).李昊睿[9]等提出了一种集合平方根滤波和四维变分(4DVAR)的混合方法来反演土壤湿度廓线，结果表明，混合方法反演的分析时刻土壤湿度廓线都优于EnSRF和4DVAR的结果.王世璋等[10]在集合平方根滤波的基础上提出了迭代集合平方根滤波，并成功应用于风暴尺度资料同化中.然而，利用数据同化方法研究混沌控制还较为少见.曹小群等[11]提出了基于MCMC方法的Lorenz混沌系统的参数估计，导出未知参数分布规律的后验概率密度函数；接着采用自适应Metropolis算法构造了Markov链；然后截取收敛的链序列，计算混沌系统参数的估计值.

文中提出一种新的数据同化方法，从卡尔曼滤波的协方差矩阵入手，在估计协方差矩阵的过程中引入Cholesky分解方法，将协方差矩阵分解为其平方根的乘积，并将这种变形的卡尔曼滤波结合Lorenz混沌系统进行同化试验.

1理论方法

1.1卡尔曼滤波

Kalman滤波作为一种顺序数据同化滤波方法，其主要步骤为：首先对模式状态进行预报，接着引入观测数据，然后利用观测数据对模式状态和误差协方差进行重新分析，得到变量的分析值.Kalman滤波的基本计算为：

1)预报.利用i-1时刻状态的分析值和误差协方差的分析值通过模型预报，得到i时刻的预报值.

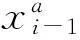
2)计算增益矩阵.利用i时刻的预报误差协方差矩阵计算增益矩阵.

其中H为观测矩阵；HT为观测矩阵的转置.

3)分析.引入观测，对状态量和误差协方差进行分析.

1.2降秩平方根滤波

降秩平方根滤波的基本思想是对状态估计的协方差矩阵P进行Cholesky分解，使协方差矩阵P=LLT，其中矩阵L具有q个特征值，且其对应的特征向量为li,i=1,…,q,算法的执行过程为：

1)随机产生状态变量.以任意的随机数作为初始样本，并以这组样本对数据同化系统进行初始化，同时导入观测数据对样本进行实时更新.

其中，xa(0)为初始状态变量分析值；La(0)为初始特征向量矩阵.

2)模型预报.通过求解样本状态的控制方程得到状态向量在第k个同化步的预报值，鉴于特征向量不是模型的状态变量模型，不能直接利用模型对其进行预报，现按(8)式将特征量投影到模型状态变量中，再用模型进行预报，系统的状态方程为：

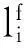
3)分析.

上式采用Cholesky分解的逆向思想，将模型预报获得的平方根矩阵Lf(k)与其转置矩阵Lf(k)T作积获得协方差矩阵Pf(k).

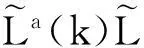
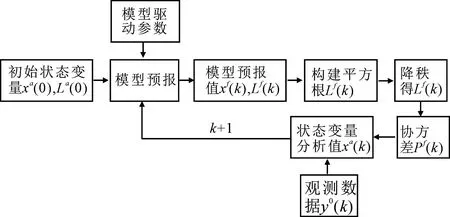
图1　降秩平方根滤波算法流程图

2数值试验

2.1Lorenz混沌系统

Lorenz混沌系统最初用于描述容器底部加热，容器内液体的运动情况.容器底部液体越来越热逐渐上升，形成对流，当容器受热到一定程度保持不变时，对流会以不规则湍流的方式运动.这个系统经过傅里叶分解、简化后，得到一个三维非线性方程组.Lorenz系统模型的数学表达式为：

(16)

其中,x为描述对流强度的量;y和z分别描述对流圈的水平和垂直方向温度梯度[12]；σ和r分别与流体的Prandtl数和Rayleigh数成比例;b为与空间相关的常数.当系统参数σ=10,b=8/3,r=28时，系统表现出混沌现象，通常采用四阶龙格库塔算法求解系统微分方程.试验以Lorenz混沌系统为预报模型，以降秩平方根滤波为同化算法，对混沌系统的状态变量进行实时估计.试验中采用均方根误差RMSE评价模型状态变量x估计值xe与真实值xt之间的差异，RMSE值越小，表明预报值与真实值越接近，同化效果越好.

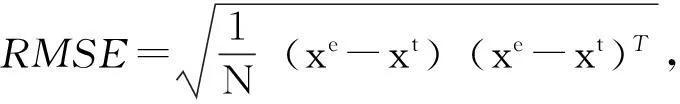
其中N为模型状态向量矩阵的大小.

2.2降秩平方根滤波基本同化试验

试验中取积分步长h=0.025，设定积分区间为[0,10]，降秩平方根滤波协方差特征根数L=30，观测间隔为1，观测方差为0.5.仅取部分状态变量值作为观测量，分别抽取0，10 h，20 h，…,400 h时刻的状态量作为n=40个观测数据，在所选取的40个观测数据上添加高斯随机数作为观测噪声，即服从N(0,1).设定系统初始状态值(x0,y0,z0)为(1.5088，-1.5312，25.4609)，图2给出了混沌系统第400步时的基本同化结果.可见真值与估计值的大致走向相同，说明通过降秩平方根滤波预报的混沌系统动力特性与混沌系统真实的动力特性基本相同，表明降秩平方根滤波用于混沌系统的状态预报是可行的.图中实线与虚线距离越近，则预报值与真值之间的误差越小，即同化效果越好.

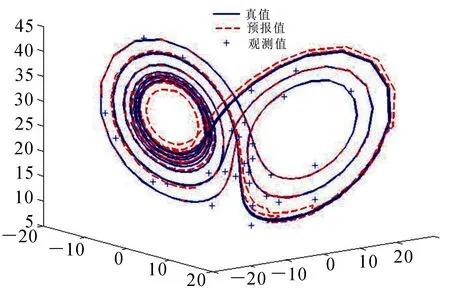
图2　第400步同化效果图

2.3观测方差对同化效果影响

为研究观测误差的变化对同化效果的影响，将试验中的观测方差设置在[0.1,1.0]之间变化，对比不同观测方差情况下的同化效果，分析观测方差增大对降秩平方根滤波同化效果的影响.图3给出了观测噪声在0.1～1.0之间变化时同化系统均方根误差的变化情况.

从图3可以看出，不同观测方差条件下的RMSE也不同，随着观测方差的增大，状态变量的RMSE值随之增加.观测方差为0.1时，RMSE值仅为0.12，观测方差为0.2时，RMSE值为0.41，曲线的走向表明观测方差越大，同化性能越差.这与应用较为广泛的集合卡尔曼滤波(EnKF)方法结论相一致.

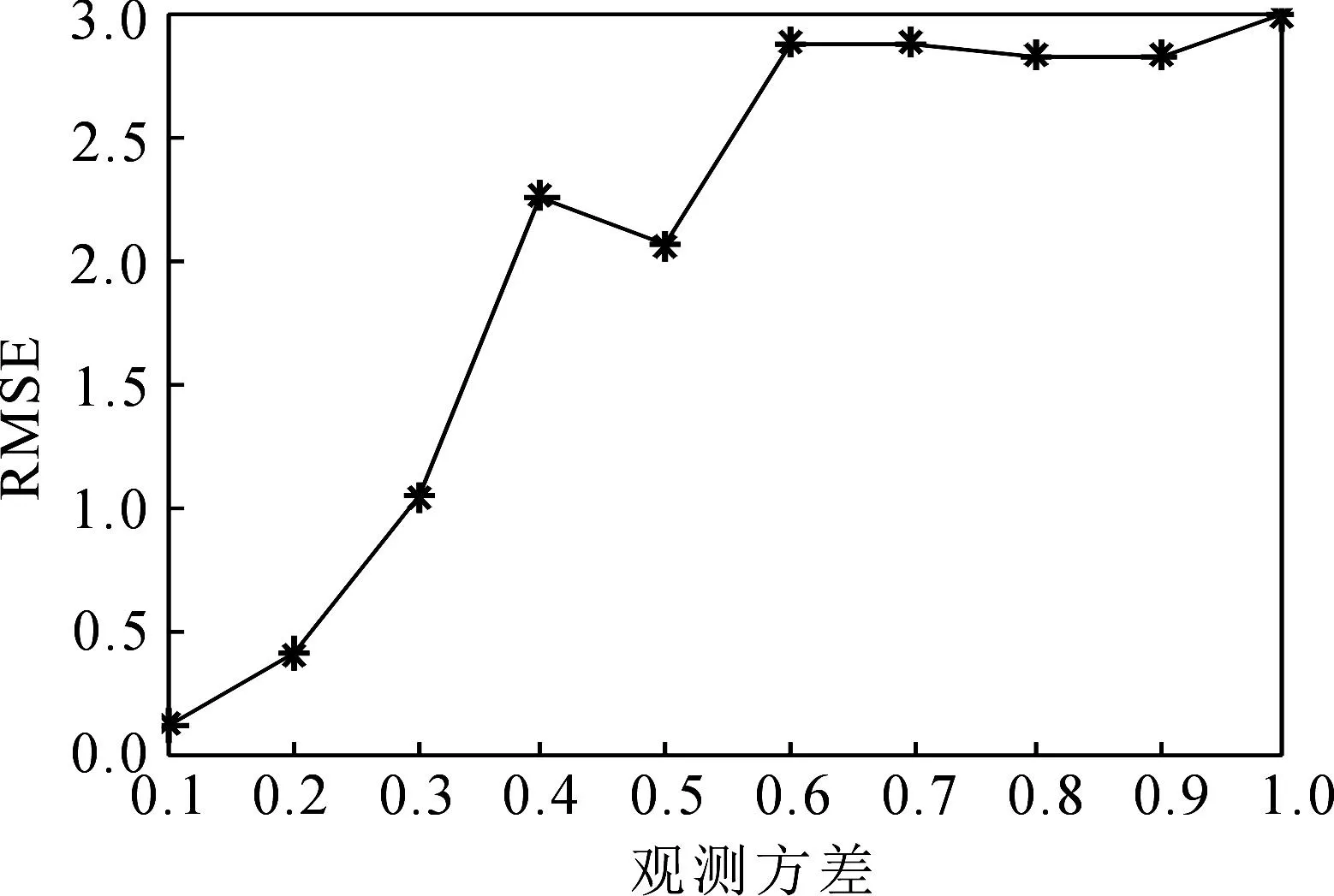
图3　观测方差对同化效果的影响

2.4观测窗口长度对同化效果影响

为研究观测窗口长度对同化效果的影响，保持上述试验设置不变而仅改变同化窗口长度，使得同化窗口长度W分别取5,15,25，对比分析同化窗口长度的改变对同化效果的影响.图4给出了系统运行400步时，同化窗口随状态变量x的RMSE值变化情况.不同的同化窗口长度使得状态变量x的RMSE值变化情况不尽相同.

1)观测窗口W=5时，系统在运行至300步之前，状态变量x的均方根误差保持在1以下，300步以后的RMSE值与300步之前相比虽有增大趋势，但RMSE值总体较小，同化效果比较稳定.

2)观测窗口W=15时，系统运行至130步后，误差明显增大，同化过程中的RMSE值与W=5时的RMSE值相比，有明显变大趋势.

3)观测窗口W=25时，系统运行至130步后，滤波出现短暂发散现象，同化过程中的RMSE值与前两个同化窗口长度相比，W=25时的RMSE明显要大很多.

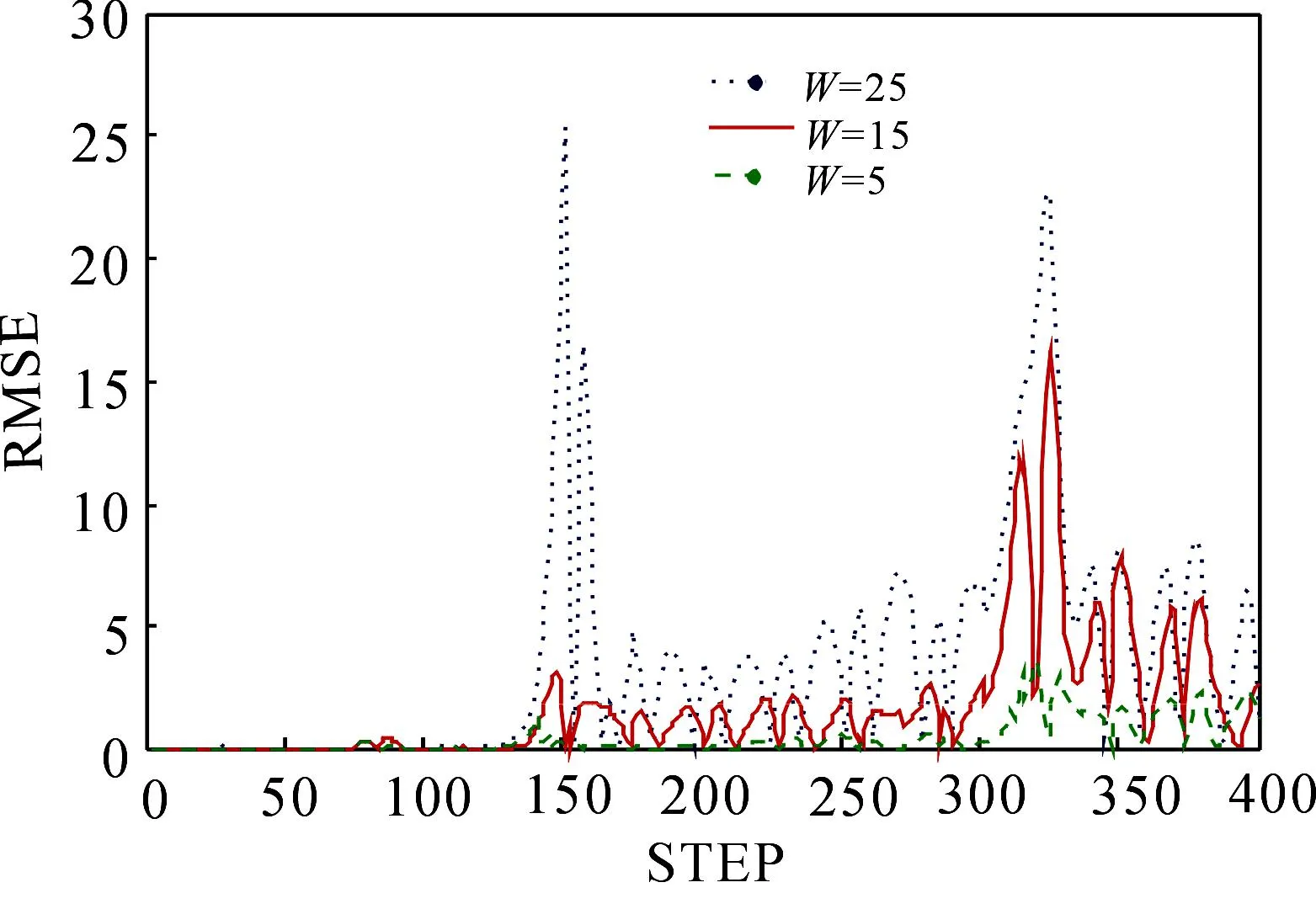
图4　观测窗口对同化效果影响

实验表明，不同的同化窗口长度对同化效果的影响不尽相同，同化窗口长度越小，系统同化效果越好.三种同化效果的差异表明，同化系统中及时利用观测数据更新模型的背景场，实时调整模型运行轨迹，对提高同化效果有很大的帮助.

2.5加密观测

考虑到滤波在局部出现较明显的发散现象，文中尝试采用加密观测的方式对系统局部状态预报进行改善.从图4可以看出，同化窗口为5时，系统在150步左右和300～400步的预报误差较大.针对这种现象，试验在0～120步同化窗口长度设定为5，120步以后采用观测加密的措施，设定同化窗口为1，图5给出了加密观测前后的比较图.

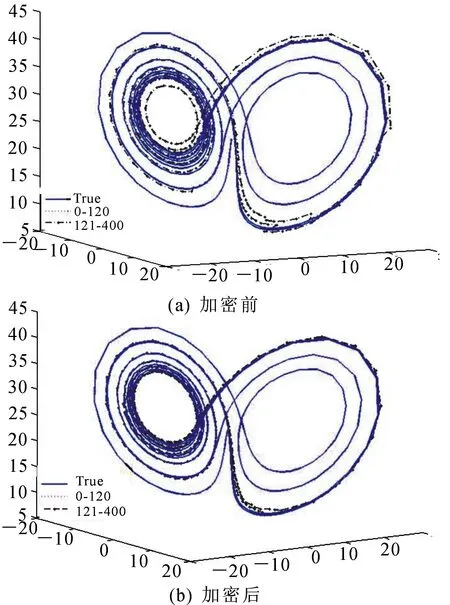
图5　采用加密观测前后比较

从图5(a)可以看出，121～400步的预报值曲线在局部地方与真值的差值较大，与图4中同化窗口W=5时反映的情况一致.图5(b)表示在121～400步采用加密观测手段后的效果图，通过对比发现，预报值的曲线更接近于真值曲线，即表明加密观测明显改善了预报效果.

2.6与集合卡尔曼滤波(EnKF)同化性能比较

为进一步研究降秩平方根滤波的同化性能，将降秩平方根滤波的性能与集合卡尔曼滤波的性能进行比较.试验中采用并行计算技术，在Lorenz混沌系统上同时用两种滤波方法对系统状态进行预报，降秩平方根滤波误差协方差的特征根数取为30，集合卡尔曼滤波的集合数为30，系统状态初始值(x0,y0,z0)仍取为(1.508870，-1.531271，25.46091)，试验中保持模型积分步长h=0.025，积分区间为[0,10]不变，依次抽取0，5，10，…，400h时刻的状态量作为N=80个观测数据，试验中仍以均值为0、方差为1的高斯随机数作为观测噪声，图6给出了每隔5步同化一次观测的试验中前400步的结果.

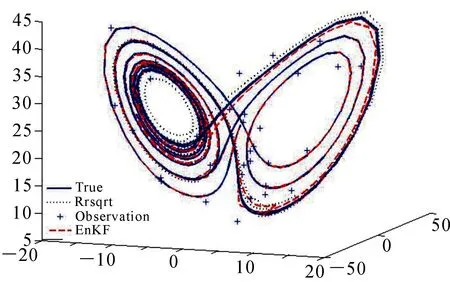
图6　两种滤波同化效果比较

从图6可以看出，两种滤波方法的状态变量曲线都接近于真值曲线，混沌现象基本相同，表明两种滤波方法都能很好地校准模型的运行轨迹.此外，从图6还可以看出，在Lorenz混沌系统图左侧部分，真值曲线与两种滤波的状态变量曲线基本处于重合状态；在Lorenz混沌系统图右侧部分，尽管两条曲线都十分接近真值曲线，但仍可清晰看出，降秩平方根滤波的状态变量曲线处于集合卡尔曼滤波状态变量曲线与真值曲线之间，即降秩平方根滤波的状态变量估计值更接近于真值.因此，降秩平方根滤波方法的同化性能在一定程度上可能优于集合卡尔曼滤波的同化性能.为进一步说明滤波性能，实验比较了不同滤波情况下，混沌系统三个状态变量x，y，z的均方根误差.图7给出了两种滤波情况下，混沌系统3个状态变量的一维同化效果比较和RMSE值变化.

图7　两种滤波同化效果对比

从图中可以看出，两种滤波方法整体较为平稳，局部均存在异常波动.降秩平方根滤波的波动幅度明显小于集合卡尔曼滤波，即短暂发散程度小于集合卡尔曼滤波，降秩平方根滤波的RMSE值小于集合卡尔曼滤波.由此可以看出，降秩平方根滤波用于三变量Lorenz混沌系统状态预报时，同化结果要优于集合卡尔曼滤波.

3结论

基于Cholesky分解方法提出了降秩平方根滤波算法，并在Lorenz混沌系统上检验了降秩平方根滤波的性能.同化试验结果表明，经Cholesky方法分解后的卡尔曼滤波在非线性系统中可以避免对模型算子和观测算子进行线性化，能够准确地更新模式预报.通过敏感性试验，研究了观测方差、同化窗口长度对同化效果的影响，比较了降秩平方根滤波和集合卡尔曼滤波的同化效果.

1)试验结果表明，经Cholesky分解的卡尔曼滤波融合模拟观测信息能够对Lorenz混沌系统状态变量进行实时更新，分解后的卡尔曼滤波同化性能稳定.

2)观测方差越小，系统同化效果越好，观测方差过大容易导致降秩平方根滤波发散.

3)文中讨论了同化窗口长度对同化效果的影响.结果表明，模型运行400步以内，随着同化窗口长度的增大，状态变量的均方根误差值会随之增大，说明在同化系统中及时、足量的观测信息对改善同化效果有很大的作用.

4)与集合卡尔曼滤波相比，分解后的降秩平方根滤波收敛速度明显提高，在系统短期运行时间内(文中为200步)，降秩平方根滤波的同化性能优于集合卡尔曼滤波，并且比集合卡尔曼滤波更稳定.

文中基于模型运行的前400步试验结果对两种同化方法的优劣进行了分析、比较.试验结果表明,混沌系统的非线性现象对同化方法有较大影响，虽与传统混沌系统研究的结论相一致，但与传统混沌系统研究相比，文中模型运行时间较短，模型长时间运行的情况需进一步讨论.此外，文中试验及上述结论均是根据简单数值试验结果得到，而降秩平方根滤波应用到大气、海洋、陆面模型中还需作进一步研究和讨论.

参考文献:

[1]LORENZEN.Deterministicnonperiodicflow[J].Journal of the Atmospheric Sciences，1963，20：130.

[2]刘福才，梁晓明.Hénon混沌系统的广义预测控制与同步快速算法[J].物理学报，2005，54(10)：4584.

[3]李丽香，彭海朋，卢辉斌，等.Hénon混沌系统的追踪控制与同步[J].物理学报，2001，50(4)：629.

[4]高山红，吴增茂，谢红琴.Kalman滤波在气象数据同化中的发展与应用[J].地球科学进展，2000，15(5)：571.

[5]KALMANRE.Anewapproachtolinearfilteringandpredictionproblems[J].Transaction of the ASME-Journal of Basic Engineering SeriesD，1960，82(2)：35.

[6]EVENSENG.Sequentialdataassimilationwithanonlinearquasi-geostrophicmodelusingMonteCarlomethodstoforecasterrorstatistics[J].Journal of Geophysical Research，1994，99(5)：10143.

[7]SAKOVP，OKEPR.Adeterministicformulationoftheensemblekalmanfilters:analternativetoensemblesquarerootfilters[J].Tellus SeriesA，2008，60(2)：361.

[8]JEFFREYS，WHITAKER，THOMASM，etal.Ensembledataassimilationwithoutperturbedobservations[J].Monthly Weather Review，2002，130(7)：1913.

[9]李昊睿，张述文，邱崇践，等.四维变分同化和集合平方根滤波联合反演土壤湿度廓线的研究[J].大气科学，2010，34(1)：193.

[10]王世璋，闵锦忠，陈杰，等.迭代集合平方根滤波在风暴尺度资料同化中的应用[J].大气科学，2013，37(3)：563.

[11]曹小群，宋君强，张卫民，等.基于MCMC方法的Lorenz混沌系统的参数估计[J].国防科技大学学报，2010，32(2)：68.

[12]薛具奎.非线性物理基础[M].兰州：兰州大学出版社，2002.

(责任编辑孙对兄)