黎曼空间型中具有常数量曲率的超曲面的刚性

刘建成，谢　逊

(西北师范大学数学与统计学院，甘肃兰州　730070)

黎曼空间型中具有常数量曲率的超曲面的刚性

刘建成，谢逊

(西北师范大学数学与统计学院，甘肃兰州730070)

摘要：设Mn为等距浸入到黎曼空间型Nn+1(c)中的具有常数量曲率的紧致超曲面，得到了数量曲率的一个估计,并应用它证明了该类超曲面的一个刚性分类结果.

关键词：黎曼空间型;数量曲率;紧致;超曲面

收稿日期：2015-05-22;修改稿收到日期:2015-10-09

E-mail:liujc@nwnu.edu.cn

基金项目:国家自然科学基金资助项目(11261051)

作者简介：刘建成(1968—),男,甘肃镇原人,教授,博士. 主要研究方向为整体微分几何与几何分析.

中图分类号：O 186.12

文献标志码：标志码：A

文章编号：章编号：1001-988Ⅹ(2015)06-0017-04

Abstract:The compact hypersurfaces with constant scalar curvature in a Riemannian space form are studied,and an estimate of constant scalar curvature is obtained.As a result of this estimation,a rigidity theorem of such hypersurfaces is proved.

Rigidity of hypersurfaces with constant scalar curvature

in Riemannian space forms

LIU Jian-cheng,XIE Xun

(College of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,Gansu,China)

Key words:Riemannian space form;scalar curvature;compact;hypersurface

0引言及主要结果

设Nn+1(c)是(n+1)维常截曲率为c的黎曼空间型.根据c>0,c=0或c<0,分别称之为球空间Sn+1(c),欧氏空间Rn+1或双曲空间Hn+1(c).

欧氏空间中具有常数量曲率的紧致超曲面的研究始于Cheng-Yau[1].一个熟知的问题是:Rn+1中具有常数量曲率的紧致超曲面是否为球面?当n=2时该问题即为经典的Liebmann定理；而当n>2时,Cheng-Yau证明了若超曲面M的截曲率K(M)>0,则结论正确；1991年，Montiel-Ros[2]证得:对于欧氏空间中的紧致连通嵌入超曲面,若有一个r阶平均曲率Hr等于常数,则Mn为全脐的,从而是一个超球面.因此在欧氏空间中,具有常数量曲率的紧致超曲面的截曲率K(M)>0是必然的.

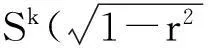
本文首先证明在黎曼空间型Nn+1(c)中具有常数量曲率的紧致超曲面的数量曲率r≥n(n-1)c，然后利用这个结论给出该类超曲面的一个刚性分类.

定理1设Mn是Nn+1(c)中数量曲率r为常数的紧致定向超曲面,则必有r-n(n-1)c≥0,当且仅当Mn为全测地时等号成立.

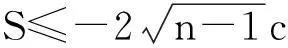
1预备知识及引理

记Rijkl为Mn的曲率张量的分量,则由Gauss方程有

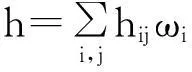
进而,

用hijk,hijkl分别表示hij的一阶和二阶共变导数的分量,则有

于是有Codazzi方程hijk=hikj和Ricci恒等式

对于Mn上的C2函数f,定义其梯度、Hessian算子及方框算子□[1]如下:

引理1[11]设Mn为Nn+1(c)的超曲面,则

引理2[12]设Mn是Nn+1(c)中具有常数量曲率的超曲面.若r-n(n-1)c≥0,则

等号成立当且仅当至少有n-1个μi相等.

2主要结果的证明

因为

所以由(5),(6)式可知

即x0正好是曲面Mn在点x0处的法矢量.

根据(7)式有

于是fij=hijx,en+1,从而由(5)式有

由于x0是超曲面Mn在x0处的法矢量,故

于是,由(8)式知Mn在x0处的第二基本形式

是恒定的二次型.

选取适当的标架,使得hij=λiδij.于是,当x,en+1x0<0时,由(8),(9)式知,第二基本形式h恒半正定.根据对称矩阵半正定的充要条件是它的特征值全为正数或零可知,Mn的所有主曲率λi(i=1,2,…,n)均为非负数.同理,当x,en+1x0>0时,第二基本形式h恒半负定,即Mn的所有主曲率λi(i=1,2,…,n)均为非正数.两种情形都表明Mn的主曲率定号,从而其数量曲率与Nn+1(c)数量曲率之差即为

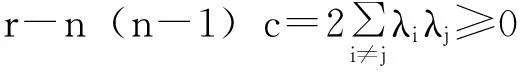
当且仅当Mn为全测地时,等号成立.由于Mn的数量曲率为常数,从而在整体上r-n(n-1)c为非负常数.】

推论1设Mn为黎曼空间型Nn+1(c)中具有常数量曲率r的紧致超曲面,则数量曲率r满足

左侧等号成立当且仅当Mn为全测地的,右侧等号成立当且仅当Mn为全脐的.

可以看出H=0时,空间型中具有常数量曲率的超曲面为全测地的.

定理2的证明由(4)式知

而根据Weitzenböck公式有

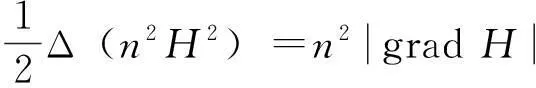
所以

另一方面,从(2)式可得Δ(n2H2)=ΔS,所以

由引理1及(10)式可得

利用引理2,引理3,从上式得到

(i)当c>0时,根据(2)式及定理 1,有

作正交变换

则

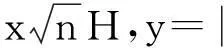
再由(11)式知

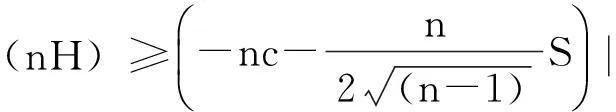
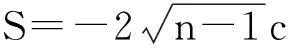
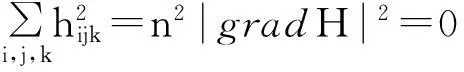
于是hijk=0,Mn具有平行第二基本形式,且主曲率λi为常数.由引理3知,Mn是至多有两个不同常主曲率的等参超曲面,且其中一个重数为1.当λ1=λ2=…=λn=H时,情形同上,Mn为全脐超曲面.当Mn有两个不同主曲率时,由文献[15]知,Mn等距于双曲柱面

H1(1-coth2t)×Sn-1(1-tanh2t),

其中t为正常数.

(iii)当c=0时,由文献[2]知Mn为全脐的.

综合以上,定理2得证.】

参考文献:

[1]CHERN Shiing-shen,YAU Shing-tung.Hypersurfaces with constant scalar curvature[J].TransAmerMathSoc,1977,225(3):195.

[2]MONTIEL S,ROS A.Compact hypersurfaces:The Alexandrov theorem for higher order mean curvatures[J].JDiffGeom,1991,52:279.

[3]CHENG Qing-ming,LI Hai-zhong,WEI Guo-xin.Embedded hypersurfaces with constantm-th mean curvature in a unit sphere[J].CommunContempMath,2010,12(6):997.

[4]BRASIL Jr A,COLARES A G,PALMAS O.Complete hypersurfaces with constant scalar curvature in spheres[J].MonatshMath,2010,161(4):369.

[5]ROS A.Compact hypersurfaces with constant scalar curvature and a congruence theorem[J].JDiffGeom,1988,27(2):215.

[6]YAU Shing-tung.Submanifolds with constant mean curvature(Ⅱ)[J].AmerJMath,1975,97(1):76.

[7]MARIA L L.Rotational hypersurfaces of space forms with constant scalar curvature[J].ManusMath,1990,67(1):285.

[8]XU Yi-wen,XU Zhi-yuan.On rigidity of Clifford torus in a unit sphere[J].ApplMathJChineseUniv,2011,26(1):121.

[9]LIU Xi-min,SU Wei-hong.Hypersurfaces with constant scalar curvature in a hyperbolic space forms[J].BalkanJGeomAppl,2002,7(1):121.

[10]WEI Si-ming,XU Hong-wei.Scalar curvature of minimal hypersurfaces in a sphere[J].MathResLett,2007,14(3):423.

[11]CHENG Qing-ming,ISHIKAWA S.Spacelike hypersurfaces with constant scalar curvature[J].ManusMath,1998,95(4):499.

[12]LI Hai-zhong.Global rigidity theorems of hypersurfaces[J].ArkMat,1997,35(4):327.

[13]OKUMURA K.Hypersurfaces and a pinching problem on the second fundamental tensor[J].AmerJMath,1974,96(1):207.

[14]HOU Zhong-hua.Hypersurfaces in a sphere with constant mean curvature[J].ProcAmerMathSoc,1997,125(4):1193.

[15]MONTIEL S.An integral inequality for compact spacelike hypersurfaces in de Sitter space and applications to the case of constant mean curvature[J].IndianaUnivMathJ,1988,37(4):909.

(责任编辑马宇鸿)