2n阶常微分方程周期边值问题解的存在唯一性

李永祥,白　静

(西北师范大学数学与统计学院,甘肃兰州　730070)

2n阶常微分方程周期边值问题解的存在唯一性

李永祥,白静

(西北师范大学数学与统计学院,甘肃兰州730070)

摘要：研究2n阶非线性常微分方程周期边值问题

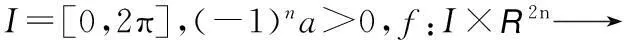
关键词：Fourier 分析法；Leray-Schauder 不动点定理；周期边值问题；解的存在唯一性

收稿日期：2015-03-22;修改稿收到日期:2015-07-17

基金项目:国家自然科学基金资助项目(11261053);甘肃省自然科学基金资助项目(1208RJZA129)

作者简介：李永祥(1963—),男，甘肃秦安人,教授,博士研究生导师.主要研究方向为非线性泛函分析与非线性微分方程.E-mail:liyx@nwnu.edu.cn

中图分类号：O 175.8

文献标志码：标志码：A

文章编号：章编号：1001-988Ⅹ(2015)06-0006-04

Abstract:This paper deals with the existence and uniqueness of solutions for 2nth-order ordinary differential equation with periodic boundary value condition

doiRis continuous and 2π-peric with respect to t.By applying the Fourier analysis method and Leray-Schauder fixed point theorem,the results of existence and uniqueness are obtained when the nonlinearity f satisifies proper growth conditions.

Existenceanduniquenessforperiodicboundary

valueproblemsof2nth-orderordinarydifferentialequations

LIYong-xiang，BAIJing

(CollegeofMathematicsandStatistics,NorthwestNormalUniversity,Lanzhou730070,Gansu,China)

Keywords:Fourieranalysismethod;Leray-Schauderfixedpointtheorem;periodicboundaryvalueproblem;existenceanduniquenessofsolutions

0引言

常微分方程周期边值问题是现代数学的一个重要分支，周期现象存在的普遍性使得这一问题的研究具有重大的理论价值和现实意义.对于一阶和二阶常微分方程，很多作者利用单调迭代法、不动点理论和上下解方法，对其周期解的存在性进行深入研究，获得了许多经典结果.文献[1]运用单调迭代法研究了方程

并获得了当其上下解存在，f是Carathéodory函数且f(t,u,v)对u,v分别满足单边Lipschitz条件时，该方程周期解的存在性.

近几年，高阶常微分方程周期解存在性的研究越来越受到人们的重视[2-8].文献[2]运用不动点指数理论和极大值原理，得到了四阶常微分方程周期边值问题(PBVP)

正解的存在性.文献[8]讨论了n阶方程

周期解的存在唯一性，推广了Duffing方程的非共振条件.

本文运用Fourier分析法和Leray-Schauder不动点定理，通过对非线性项f所满足增长条件的讨论，获得了2n阶常微分方程周期边值问题

(1)

1准备工作

给定h∈H，考虑2n阶线性周期边值问题(LPBVP)

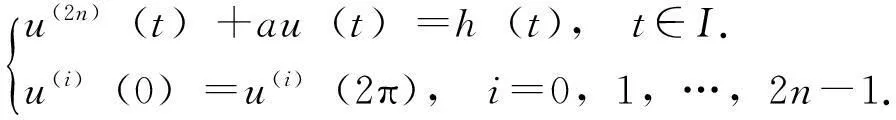
(2)

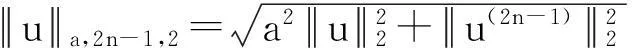
(2) 对∀h∈H，LPBVP(2)的唯一解u∈W2n,2(I)满足：

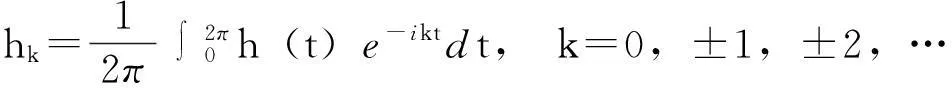
设u=Sh，则u∈W2n,2(I)是LPBVP(2)的唯一解.显然，u与u(m)(m=1,2,…,2n-1)都可展为Fourier级数.设

则由Fourier系数的积分公式，有

因此，由u(2n)(t)+au(t)=h(t)可知，

根据Fourier展式的唯一性可得，

由Parseval等式，有

当n=2l+1(l∈N)时，

当n=2l(l∈N)时，

从而

所以

(2) 对∀1≤m≤2n-1，由(4)式以及Parseval等式，有

所以

2主要结果及其证明

定理1设f∈C(I×R2n,R),若f满足增长条件：

其中M>0,ci≥0(i=0,1,…,2n-1)且ci满足

则PBVP(1)有解.

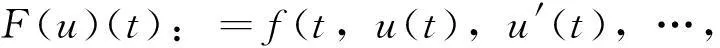
考察方程簇

设u∈X是方程簇(9)中某一λ∈(0,1)相应的方程的解.令h=λF(u)，则由S的定义可知u=Sh∈W2n,2(I)是LPBVP(2)的唯一解.由引理1(1)，有

由(8)式，(6)式以及(3)式，有

结合(10)式，易得

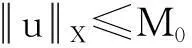
定理2设f∈C(I×R2n,R)，若对∀t∈I,(x0,x1,…,x2n-1),(y0,y1,…,y2n-1)∈R2n，非线性项f满足Lipschitz条件：

其中c0,c1,…,c2n-1满足(7)式，则PBVP(1)有唯一解.

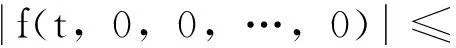
即条件(6)成立.又c0,c1,…,c2n-1满足(7)式,所以由定理1可知，PBVP(1)有解.

下证唯一性，设u1,u2∈C2n(I)是PBVP(1)的两个解.设ui=S(F(ui)),i=1,2，则由(8)式及(11)式，可得

由于u2-u1是LPBVP(2)中h=F(u2)(t)-F(u1)(t)对应的解，所以由(12)式和(3)式，有

从而，结合引理1(1)，有

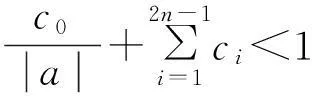
在定理1中，如果条件(6)加强为：存在M>0,ci≥0(i=0,1,…,2n-1)，使得

则有如下结论成立：

定理3设f∈C(I×R2n,R)，若f满足条件(13)，ci满足(7)式，则PBVP(1)有解.

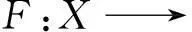
设u∈X是方程簇(9)中某一λ∈(0,1)相应的方程的解.令h=λF(u)，则(10)式成立.按S的定义可知，u=Sh∈W2n,2(I)是LPBVP(2)的唯一解.由(8)式，(13)式以及(3)式，得

结合(10)式,有

所以

即方程簇(9)的解集在X中有界.因此，由Leray-Schauder不动点定理，A有不动点，该不动点是PBVP(1)在C2n(I)中的解.】

若偏导数fx0,fx1,…,fx2n-1存在，则由定理2和微分中值定理可得

推论1设f∈C(I×R2n,R)，偏导数fx0,fx1,…,fx2n-1存在，若存在ci>0使得

且ci满足(7)式，则PBVP(1)有唯一解.

参考文献:

[1]JIANGDa-qing,FANMeng,WANA-ying.Amonotonemethodforconstructingextremalsolutionstosecond-orderperiodicboundaryvalueproblems[J].J Com Appl Math,2001,136(1):189.

[2]LIYong-xiang.Positivesolutionforfourth-orderperiodicboundaryvalueproblems[J].Nonl Anal,2003,54(6):1069.

[3]CONGFu-zhong.Existenceofperiodicsolutionof(2n+1)th-orderordinarydifferentialequation[J].Appl Math,2004,17(6):727.

[4]LIYong-xiang,YANGHe.Existenceanduniquenessofperiodicsolutionforodd-orderordinarydifferentialequations[J].Ann Polon Math,2011,2(100):105.

[5]CONGFu-zhong,HUANGQing-dao,SHIShao-yun.Existenceanduniquenessofperiodicsolutionfor(2n+1)th-orderdifferentialequations[J].J Math Anal Appl,2000,241(1):1.

[6]CABADAA.Themethodofloweranduppersolutionsfornth-orderperiodicboundaryvalueproblems[J].J Appl Math Stoch Anal,1994,7:33.

[7]LIYong-xiang.Existenceanduniquenessforhigherorderperiodicboundaryvalueproblemunderspectralseperationconditions[J].J Math Anal Appl,2006,322(2):530.

[8]LIYong-xiang,MUJia.Oddperiodicsolutionsfor2nth-orderordinarydifferentialequations[J].Non Anal Appl,2010,73(10):3268.

(责任编辑马宇鸿)